Двойные интегралы

1.

Двойной интеграл
Основные понятия
Геометрический смысл двойного интеграла
Основные свойства двойного интеграла
Вычисление двойного интеграла в декартовых
координатах

2.

Основные понятия
Пусть в замкнутой области D плоскости XOY задана
непрерывная функция z = f(x, y).
y
Разобьем область D на n
«элементарных областей» Di,
площади которых обозначим через
ΔSi , а диаметры (наибольшее
расстояние между точками области)
через di.
Di
В каждой области Di выберем
произвольную точку Mi (xi ; yi ).
D
Mi (xi ; yi )
Составим сумму вида:
0
x
n
f ( x , y ) S f ( x , y ) S f ( x , y ) S f ( x , y ) S
i 1
i
i
i
1
1
1
2
2
2
n
n
n

3.

Основные понятия
Эта сумма называется интегральной суммой функции f (x, y) в
области D.
Рассмотрим предел интегральной суммы, когда n стремится к
бесконечности, таким образом, что
max d i 0
Если этот предел существует и не зависит от способа
разбиения области D на части, ни от выбора точек в них, то
он называется двойным интегралом от функции f (x; y) по
области D и обозначается:
D f ( x; y)dxdy D f ( x; y)dS

4.

Основные понятия
Таким образом, двойной интеграл определяется равенством:
n
f ( x; y) dxdy lim f ( x ; y ) S
D
n
max d i 0 i 1
i
i
i
Функция f(x; y) называется интегрируемой в области D,
D – область интегрирования, x; y – переменные интегрирования,
dxdy (или dS) – элемент площади.
Для всякой ли функции существует двойной интеграл? На этот
вопрос дает ответ теорема:
Теорема
Если функция z = f(x; y) непрерывна в замкнутой области D, то
она интегрируема в этой области (достаточное условие
интегрируемости функций).

5.

Геометрический смысл двойного
z = f(x; y)
интеграла
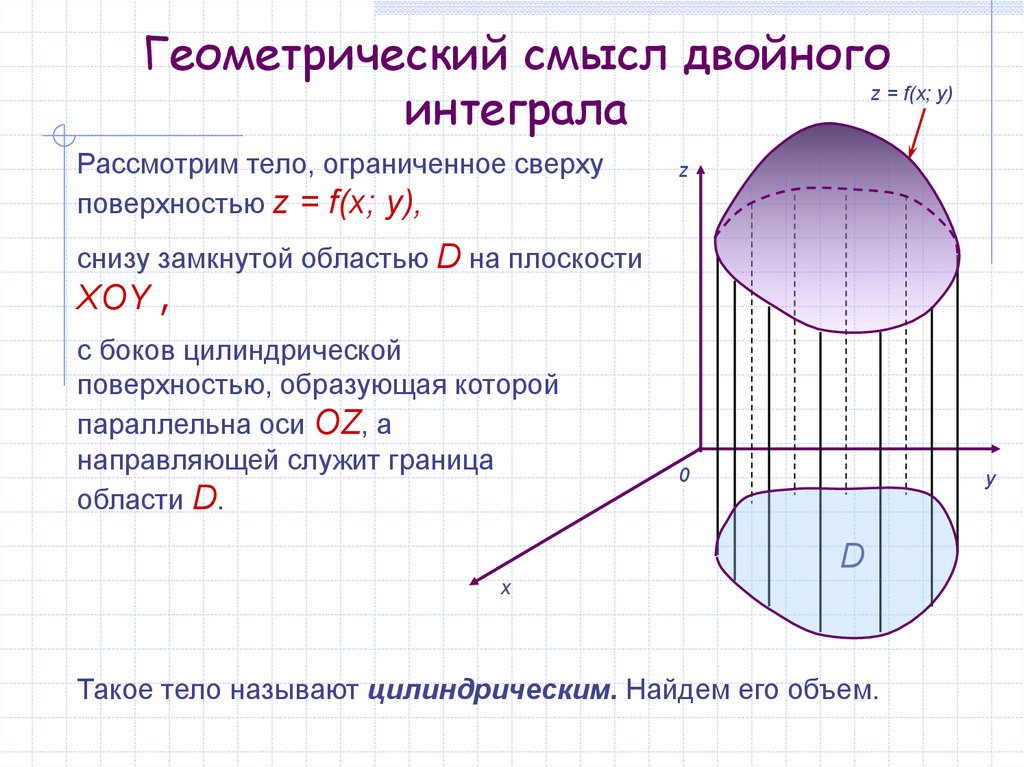
Рассмотрим тело, ограниченное сверху
поверхностью z = f(x; y),
z
снизу замкнутой областью D на плоскости
XOY ,
с боков цилиндрической
поверхностью, образующая которой
параллельна оси OZ, а
направляющей служит граница
области D.
0
y
D
x
Такое тело называют цилиндрическим. Найдем его объем.

6.

Геометрический смысл двойного
интеграла
f (xi ; yi)
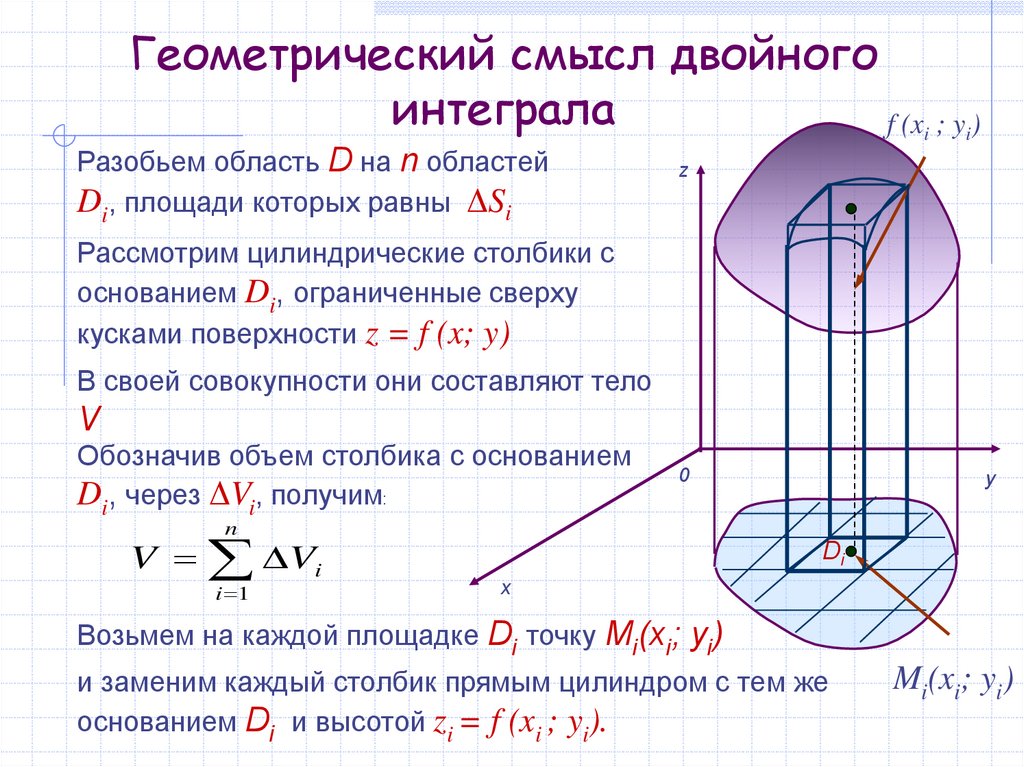
Разобьем область D на n областей
Di, площади которых равны ΔSi
z
Рассмотрим цилиндрические столбики с
основанием Di, ограниченные сверху
кусками поверхности z = f (x; y)
В своей совокупности они составляют тело
V
Обозначив объем столбика с основанием
Di, через ΔVi, получим:
0
y
n
V Vi
i 1
Di
x
Возьмем на каждой площадке Di точку Mi(xi; yi)
и заменим каждый столбик прямым цилиндром с тем же
основанием Di и высотой zi = f (xi ; yi).
Mi(xi; yi)

7.

Геометрический смысл двойного
интеграла
Объем этого цилиндра
цилиндрического столбика
Vi f ( xi ; yi ) Si
приближенно
Тогда получаем: V
равен
n
ΔVi
объему
n
V f ( x ; y ) S
i 1
i
i 1
i
i
Это равенство тем точнее, чем больше число n и чем меньше
размеры элементарных областей, поэтому:
V lim
n
f ( x ; y ) S f ( x; y)dxdy
n
max d i 0 i 1
i
i
i
D
i

8.

Свойства двойного интеграла
1
f ( x; y) f ( x; y) dx dy f ( x; y) dx dy f ( x; y) dx dy
1
2
1
D
2
D
D
k f ( x; y)dxdy k f ( x; y)dxdy
D
3
2
D
y
Область интегрирования двойного
интеграла можно разбить на части,
т.е. если область D состоит из двух
областей D1 и D2, то
D1
D2
0
f ( x; y)dxdy f ( x; y)dxdy f ( x; y)dxdy
D
4
dS S
D
D1
D2
x

9.

Свойства двойного интеграла
5
Если в области D имеет место неравенство:
f ( x; y ) 0
f ( x; y)dxdy 0
D
6
Если в области D функции f(x; y) и g(x; y) удовлетворяют
неравенству:
f ( x; y ) g ( x; y )
f ( x; y)dxdy g ( x; y)dxdy
D
7
D
Если функция f(x; y) непрерывна в замкнутой области D,
площадь которой S то:
mS f ( x; y)dxdy MS
D
где m и M соответственно наименьшее и наибольшее
значение подынтегральной функции в области D.

10.

Свойства двойного интеграла
8
Если функция f(x; y) непрерывна в замкнутой области D,
площадь которой S, то в этой области существует такая точка
(x0 ; y0), что
f ( x; y)dxdy f ( x ; y ) S
0
D
Величину
0
1
f ( x0 ; y0 ) f ( x; y )dxdy
S D
называют средним значением функции f(x ; y) в области D.

11.

Вычисление двойного интеграла в
декартовых координатах
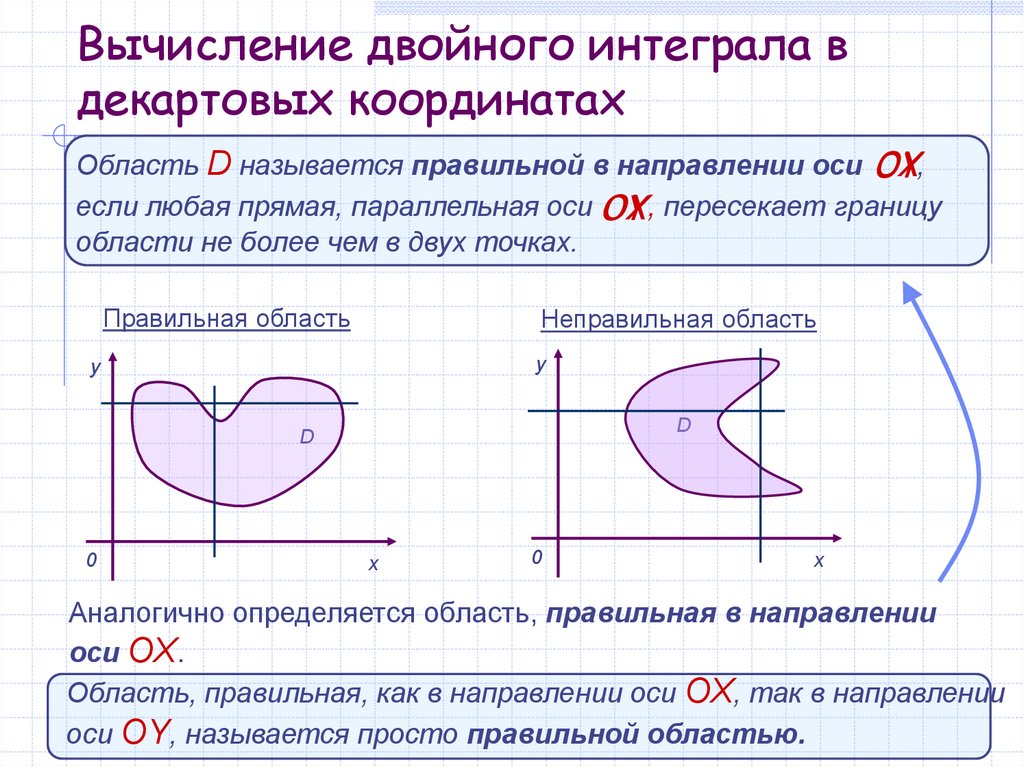
Область D называется правильной в направлении оси ОY
ОX,
если любая прямая, параллельная оси ОY
ОX , пересекает границу
области не более чем в двух точках.
Правильная область
Неправильная область
y
y
D
D
0
x
0
x
Аналогично определяется область, правильная в направлении
оси OX.
Область, правильная, как в направлении оси OX, так в направлении
оси OY, называется просто правильной областью.

12.

Вычисление двойного интеграла в
декартовых координатах
y
(1)
d
D
c
x
0
a
b
(2)

13.

Вычисление двойного интеграла в
декартовых координатах
2) Пусть область D ограничена прямыми x = a, x = b (a < b) и
кривыми y = φ1(x), y = φ2(x), причем функции φ1(x) и φ2(x)
непрерывны и таковы, что
1( x ) 2 ( x )
x a, b
Таким образом задается область,
правильная в направлении оси OY.
Или эта область называется простой
относительно оси Ох.
f ( x; y )dxdy dx f ( x, y )dy
D
y
y = φ22(x)
D
0
a
(3)
y = φ1(x)
b
x

14.

Вычисление двойного интеграла в
декартовых координатах
(3)
Формула (3) представляет собой способ вычисления двойного
интеграла в декартовых координатах.
Правую часть формулы (3) называют двукратным
повторным) интегралом от функции f(x, y) по области D.
(или
Для вычисления двукратного интеграла сначала берем внутренний
интеграл, считая x постоянным,
затем берем внешний интеграл, то есть результат первого
интегрирования интегрируем по x в пределах от a до b.

15.

Вычисление двойного интеграла в
декартовых координатах
3) Пусть область D ограничена прямыми y = c, y = d (c < d) и
кривыми x = ψ1(y), x = ψ2(y), причем функции ψ1(y) и ψ2(y)
непрерывны и таковы, что
1 ( y) х 2 ( y)
y c, d
y
x = ψ11(x)
d
Таким
образом
задается
область,
правильная в направлении оси OX или
простая относительно оси Оу.
При вычислении внутреннего
интеграла считаем
y = const
D
x = ψ22(x)
c
0
f ( x; y) dx dy dy f ( x, y)dx
x
(4)
D
! Интегрирование сначала выполняется по переменной х, а затем по переменной у!

16.

Пример 1. Вычислить повторный интеграл
3
x 2 4
1
2
dx
Воспользуемся формулой (3):
1
dy
2
x
3
x2 4
1
2
dx
3
1
dy
2
x
1
x 4 1
2 dy dx
2 x
2
Вычислим сначала внутренний интеграл по переменной у, считая х=const:
x2 4
2
1
1
dy 2
2
x
x
x2 4
2
2
1
1
x
2
x 4
2
2
dy
y
x
4
2
1
2
x
.
2
2
2
2
2
x
x
x
Вычислим теперь внешний интеграл по переменной х, подставив в него
полученное выражение:
1 2 x
3
1
2
3
2
2 2
1
1
dx x 3 1 2 1 3 .
x 1
3 1
3
3

17.

Пример 2. Вычислить двойной интеграл
x y dx dy
D
по области D, ограниченной прямыми х=2,
х=6, у=1, у=4.
Область D является простой относительно осей Ох и
Оу (рисунок), поэтому для вычисления интеграла
можно использовать любую из формул (1) или (2).
Вычислим сначала двойной интеграл по формуле (1):
6
4
2
1
x y dx dy dx x y dy
D
Вычислим внутренний интеграл по переменной у при х=const:
4
y
42
12
1
1 x y dy xy 2 4 x 2 1x 2 4 x 8 x 2 3x 7,5.
1
4
2

18.

Пример 2. Вычислить двойной интеграл
Вычислим теперь внешний интеграл по переменной
х, подставив в него полученное выражение:
6
3x
3 62
3 22
2 3x 7,5 dx 2 7,5 x 2 7,5 6 2 7,5 2 78
2
6
2
Теперь вычислим двойной интеграл по формуле (2): 4
6
x y dx dy dy x y dx
D
1
2
Вычислим внутренний интеграл по переменной х при у=const:
6
x
62
22
4 y 16.
x
y
dx
yx
6
y
2
y
2
2
2 2
2
6
2
Внешний интеграл:
4
2
2
2
4
y
16
dy
2
y
16
y
2
4
16
4
2
1
16 1 78.
1
4
1

19.

Пример 3. Вычислить двойной интеграл
x y dx dy
2
D
Область D является простой относительно осей Ох и Оу
(рисунок), поэтому вычислим интеграл по формуле (3).
x y dx dy dx x y dy
3
9
2
2
D
0
x2
Вычислим внутренний интеграл по переменной у при х=const:
2 2
2
2 9 2 2 x
y
1 4 81
2
2
2 x y dy x y 2 2 9 x 2 x x 2 9 x 2 x 2 .
x
x
9
2
9
2
Вычислим теперь внешний интеграл по переменной х, подставив в него
полученное выражение:
3
2 1 4 81
3 1 5 81 3 1 5 81
9
x
x
dx
3x x x 3 3 3 3 0 64,8.
0
2
2
10
2 0
10
2
3

20.

Пример 3. Вычислить двойной интеграл
y
x
D x y dx dy 0 dy 0 x y dx 0 3 yx dy
0
9
y
2
9
3
2
9
3
1
2
1
2
2 y
2 2
y y dy y dy
y
3
3
30
3 1
3 5
0
2
0
9
3
2
3
2
9
3
2
5 9
2
0
4 2 52
4 35
4 81
324
3
64,8.
15
15
5
5

21.

Пример 4.
Вычислить
( x 2y ) dxdy
y
y 0;
2
D
y x 2;
D:
y 2 x
Воспользуемся формулой (4)
xy = x2 yy
1
yx = 22 -- xyy
D
1
00
( x 2y ) dxdy dy ( x 2y ) dx
D
2
2 y
x
dy 2yx
2
y
0
1
2
(2 y )2
y
постоянная
2y (2 y ) 2y y dy
2
2
0
1
x

22.

Вычисление двойного интеграла в
декартовых координатах
3
2
y
y
2
2
2 2y
4 y 2y 2y dy
2
2
0
1
3
3y 2 3y
2
2
2y dy
2
2
0
1
y 3 3y 2 4y
2y
2
4
5
5
2
1
1 3 4
2 1,45
2 4 5
0

23.

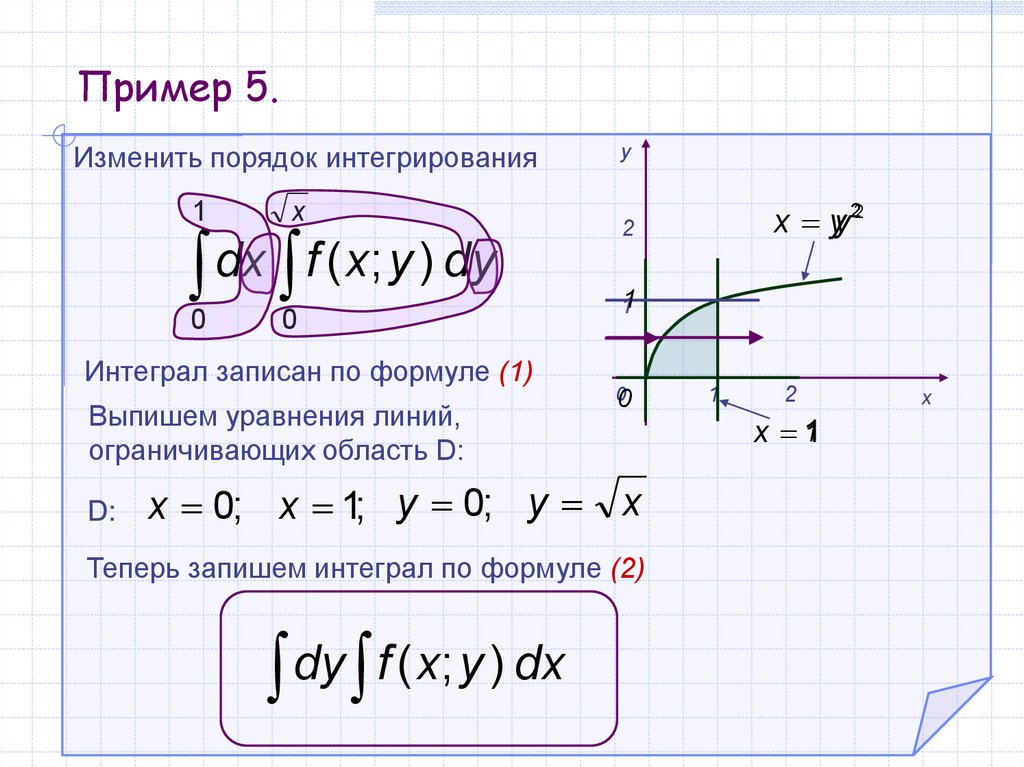
Пример 5.
Изменить порядок интегрирования
1
x
0
0
dx f ( x; y ) dy
Интеграл записан по формуле (1)
Выпишем уравнения линий,
ограничивающих область D:
y
11
00
x 0; x 1; y 0; y x
Теперь запишем интеграл по формуле (2)
dy f ( x; y ) dx
x yy22
2
1
2
x 1
x

24.

Пример 6. Изменить порядок интегрирования
в двойном интеграле