Similar presentations:
Математический анализ
1. Физика. Математика. Лекция 1 Математический анализ
Лектор: ЗЕЛЕЕВ МАРАТ ХАСАНОВИЧ2. Понятие числовой функции
• Переменной величиной будем называть числовуювеличину, которая в изучаемой задаче
принимает различные значения. Величина,
принимающая только одно значение, есть
частный случай переменной. Ее называют
постоянной величиной или константой.
• Если в изучаемой задаче несколько переменных, то
различают зависимые и независимые переменные.
Таковыми переменные являются лишь по
отношению друг к другу, и их различие
определяется условием задачи.
3.
Если каждому числу x ставится в соответствие одно,определенное по правилу f, число – значение числовой
переменной y, то говорят, что на множестве X задана
однозначная функция, или просто функция, и пишут
y=f(x) x ∈ X.
Переменную x называют аргументом, множество X –
областью определения функции .
Множество всех значений переменной y, поставленных в
соответствие значениям аргумента x из множества X,
называют множеством значений функции y = f(x).
Обозначим его буквой Y.
Функция y=f(x) полностью определена, если известна
область ее определения X и для каждого значения
аргумента x из области определения X известно
соответствующее ему значение y или известно правило f,
по которому может быть найдено это значение.
4.
5.
6.
7.
f(x0 + x)8.
Замечание: Разность двух функций бесконечно большихпри x → a ,имеющих значения одинаковых знаков,
неопределена; неопределены также частное двух
бесконечно больших функций, частное двух бесконечно
малых функций, произведение бесконечно малой и
бесконечно большой функций. В этом случае говорят о
неопределенностях вида:
.
Для нахождения предела выражения следует
раскрыть соответствующую неопределенность.
9. Замечательные пределы
10.
11.
12.
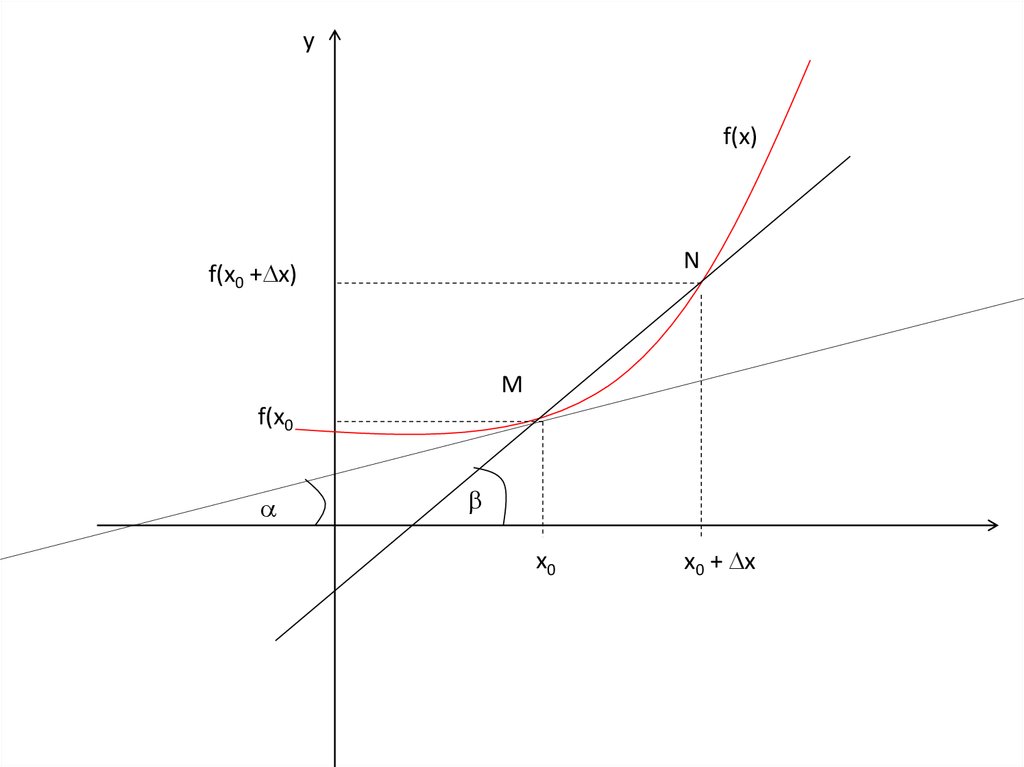
уf(x)
N
f(x0 + x)
M
f(x0
x0
x0 + x
13.
Пусть f(x) определена на некотором промежутке (a, b).Тогда тангенс угла наклона секущей МР к графику
функции.
f
lim tg lim
f ( x0 ) tg ,
x 0
x 0 x
где - угол наклона касательной к графику функции f(x) в
точке (x0, f(x0)).
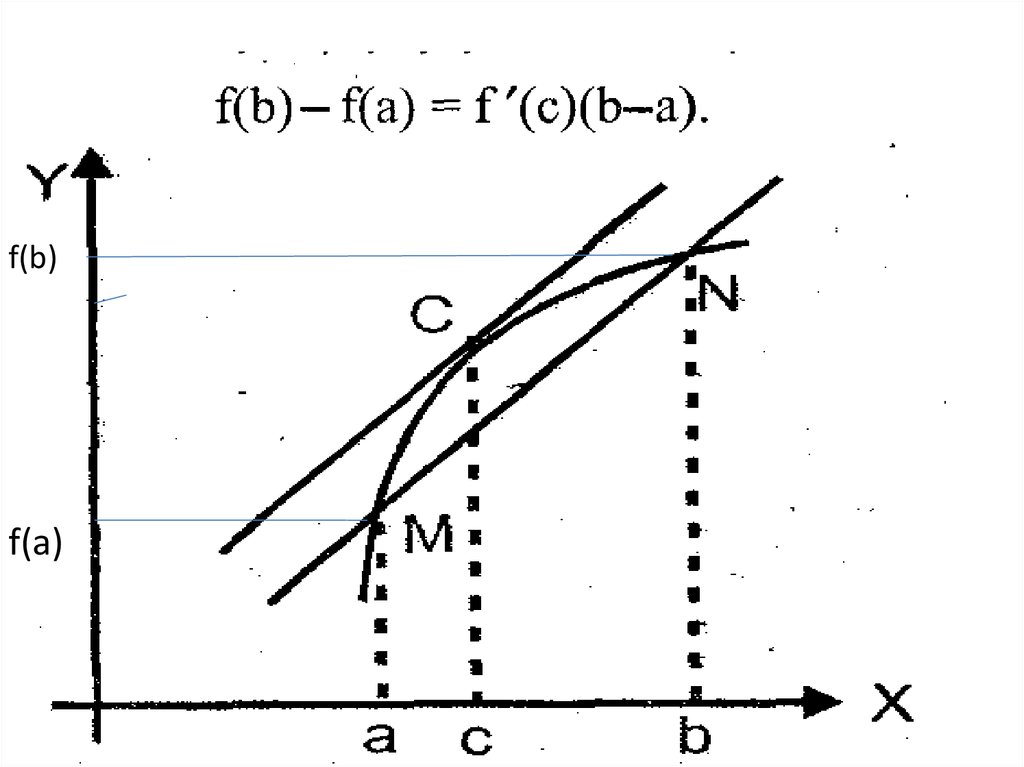
14.
f(b)f(a)
15.
16.
17.
Производные основных элементарных функций.1)С = 0;
2)(xm) = mxm-1;
1
3) x
2 x
1
1
4) 2
x
x
5) e x e x
a
6) a
x
x
ln a
1
7) ln x
x
1
8) log a x
x ln a
9) sin x cos x
10) cos x sin x
1
11) tgx
cos 2 x
12) ctgx
13) arcsin x
14) arccos x
1
sin 2 x
1
1 x2
1
1 x2
1
15) arctgx
1 x2
1
16) arcctgx
1 x2
18.
Производная сложной функции.Теорема. Пусть y = f(x); u = g(x), причем область значений функции u входит в
область определения функции f.
Тогда
y f (u ) u
Пример. Найти производную функции
1 2
y x cos x sin x cos x
2
.
Сначала преобразуем данную функцию:
y
1
1
sin 2 x
cos 2 x
2
2
1
1
1
1
y sin 2 x x2 cos 2 x 2 cos x( sin x) sin 2 x x cos 2 x sin x cos x x cos 2 x.
2
2
2
2
19.
20.
21.
22.
Интегральное исчисление.Первообразная функция.
Функция F(x) называется первообразной функцией
функции f(x) на отрезке [a, b], если в любой точке
этого отрезка верно равенство:
F (x) = f(x).
Надо отметить, что первообразных для одной
и той же функции может быть бесконечно много.
Они будут отличаться друг от друга на некоторое
постоянное число.
F1(x) = F2(x) + C.
23.
Неопределенный интеграл.Определение: Неопределенным
интегралом функции f(x) называется
совокупность первообразных
функций, которые определены
соотношением:
F(x) + C.
Записывают: f ( x)dx F ( x) C;
24.
Свойства:f ( x)dx (F ( x) C) f ( x);
2. d f ( x)dx f ( x)dx;
1.
3. dF ( x) F ( x) C;
4. (u v w)dx udx vdx wdx; где u, v, w – некоторые функции от х.
1.
C f ( x)dx C f ( x)dx;
1 3
Пример: ( x 2 sin x 1)dx x dx 2 sin xdx dx x 2 cos x x C;
3
2
2
25.
1Интеграл
tgxdx
2
ctgxdx
3
x
a
dx
4
dx
a2 x2
dx
x2 a2
dx
5
6
x2 a2
7
x
dx
8
dx
x
Значение
-ln cosx +C
9
Интеграл
x
e
dx
Значение
ex + C
ln sinx + C
10
cos xdx
sinx + C
ax
C
ln a
1
x
arctg C
a
a
1 x a
ln
C
2a x a
11
sin xdx
-cosx + C
12
ln x x 2 a 2 C
14
1
cos 2 x dx
1
sin 2 x dx
dx
x 1
C , 1
1
15
ln x C
13
16
a2 x2
1
cos x dx
1
sin x dx
tgx + C
-ctgx + C
x
arcsin + C
a
x
ln tg C
2 4
x
ln tg C
2
26.
Методы интегрированияНепосредственное интегрирование.
27.
Способ подстановки (замены переменных).Пример. Найти неопределенный интеграл
Сделаем замену t = sinx, dt = cosxdt.
2 3/ 2
2 3/ 2
1/ 2
t dt t dt 3 t C 3 sin x C.
sin x cos xdx .
28. Интегрирование по частям.
Способ основан на известной формуле производной произведения:(uv) = u v + v u
где u и v – некоторые функции от х.
В дифференциальной форме: d(uv) = udv + vdu
Проинтегрировав, получаем:
d (uv) udv vdu , а в соответствии с приведенными
выше свойствами неопределенного интеграла:
uv udv vdu
или
udv uv vdu ;
29.
2u
x
; dv sin xdx;
2
2
Пример. x sin xdx
x
cos x cos x 2 xdx
du 2 xdx; v cos x
u x; dv cos xdx;
2
2
x cos x 2 x sin x sin xdx x cos x 2 x sin x 2 cos x C.
du dx; v sin x
30. Определенный интеграл. Пусть на отрезке [a, b] задана непрерывная функция f(x).
31.
Если S nn
f ( ) x , то
i
i 1
i
n
lim
max xi 0
f ( ) x S.
i 1
i
i
• Если для функции f(x) существует предел то
функция называется интегрируемой на отрезке
[a, b].
b
n
lim
max xi 0
f ( ) x f ( x)dx,
i 1
i
i
a
32.
Свойства определенного интеграла.b
b
a
a
Af ( x)dx A f ( x)dx;
b
( f ( x) f
1
a
2
b
b
a
a
( x))dx f1 ( x)dx f 2 ( x)dx
a
f ( x)dx 0
a
•Если f(x) (x) на отрезке [a, b] a < b, то
b
b
a
a
f ( x)dx ( x)dx

























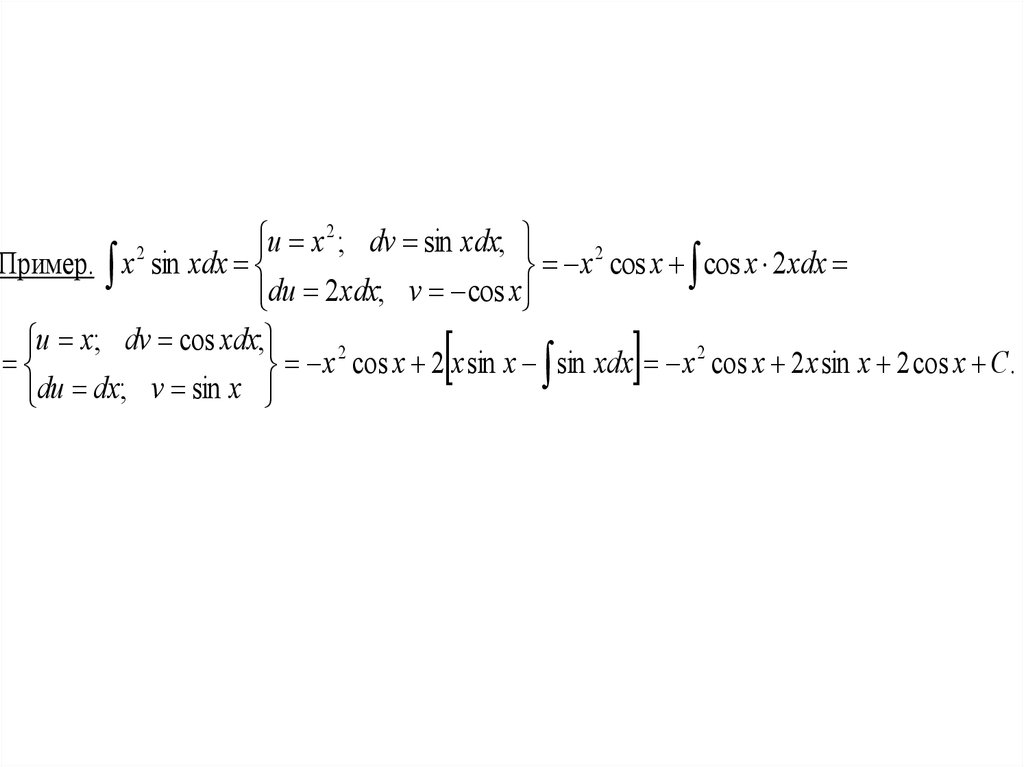
![Определенный интеграл. Пусть на отрезке [a, b] задана непрерывная функция f(x). Определенный интеграл. Пусть на отрезке [a, b] задана непрерывная функция f(x).](https://cf.ppt-online.org/files/slide/s/S2kgnNsdlA7yHYV8ZOR3pCmKqibJ1EhLXjvr5Q/slide-29.jpg)


 mathematics
mathematics








