Similar presentations:
Основы математического анализа
1.
Лекция 1. Основыматематического анализа
Лектор: Войтик Виталий
Викторович
2.
Литература• Лобоцкая Н.Л. Основы высшей математики
2015, Москва
• Ремизов А.Н. Максина А.Г., Потапенко А.Я.
Медицинская и биологическая физика
2013, Москва
• Ремизов А.Н., Максина А.Г. Сборник задач
по медицинской и биологической физике
2014, Москва
• Антонов В.Ф. Физика и биофизика
(http://www.studmedlib.ru/boo
k/ISBN9785970426777.html ) 2013, Москва
3.
Определение производнойЕсли существует предел отношения
f (x x) f (x)
lim
,
x 0
x
то функция f(x) называется
дифференцируемой в точке х, а значение
предела называется производной от
функции f(x) в точке х и обозначается
f (x x) f (x)
df
lim
f (x) f x
x 0
x
dx
4.
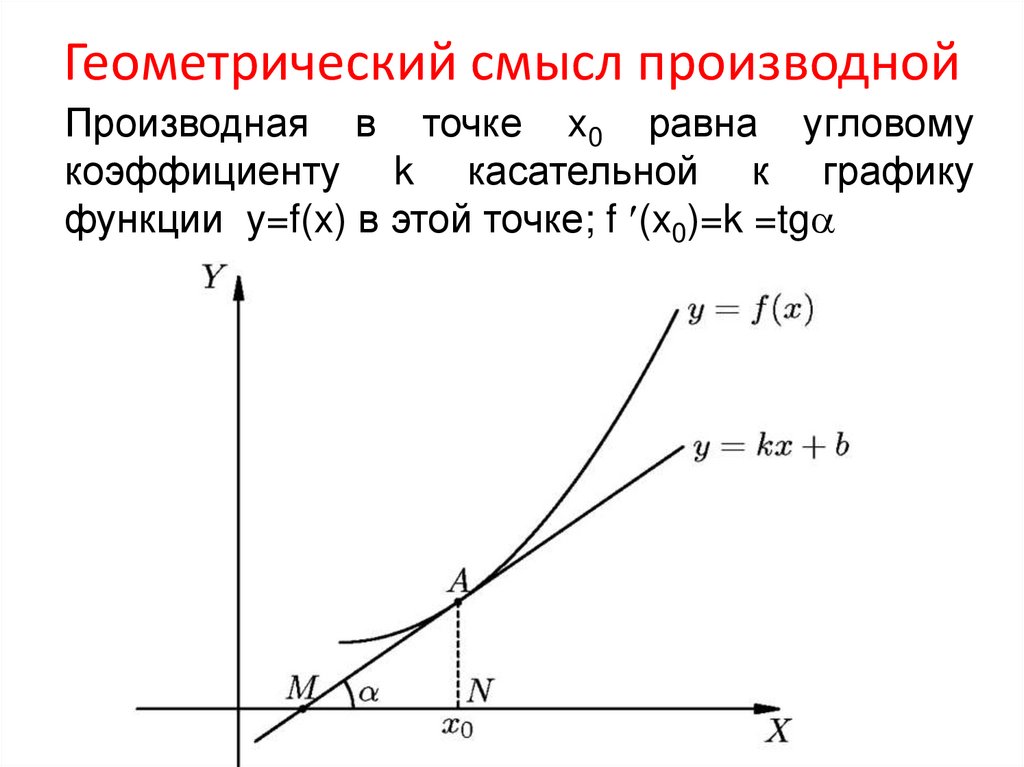
Геометрический смысл производнойПроизводная в точке x0 равна угловому
коэффициенту k касательной к графику
функции y=f(x) в этой точке; f (x0)=k =tg
5.
Правила дифференцирования1)
c1f1 (x) c2f2 (x) c1f1 (x) c2f 2 (x)
2)
f (x) g(x) f (x)g(x) f (x)g (x)
3)
f(x) f (x)g(x)-f(x)g (x)
=
2
g (x)
g(x)
6.
Производные элементарных функцийC 0; sin x cos x; cos x sin x;
x 1;
1
;
n
n 1 tgx
2
x nx ;
cos x
arcsin
x
x
n n ln n;
x
1
ln x ;
x
1
1 x
2
arccos
x
;
x
e e ;
x
ctg
x
arctgx
arcctgx
1
.
2
1 x
1
;
2
sin x
1
1 x2
;
1
;
2
1 x
7.
Производная сложной функцииЕсли y=f(g(x)), то y f (u) u (x)
где u=g(x)
Пример. Найти производную функции
.
1
2
y x cos x sin x cos x
2
Сначала преобразуем данную функцию:
x
1
1
1
y sin 2x cos 2 x ;
y sin 2x x 2 cos 2x
2
2
2
2
1
1
2cos x ( sin x) sin 2x x cos 2x sin x cos x x cos 2x
2
2
8.
Дифференциал функцииДифференциалом df(x) функции f(x) в
точке х называется произведение
производной от функции f(x) в этой
точке на величину приращения
аргумента х
df (x) f (x)dx
9.
Связь между дифференциаломфункции и её приращением
Дифференциал функции, в общем случае
отличаясь от приращения функции, представляет
собой главную часть этого приращения,
линейную относительно приращения аргумента.
В этом заключается аналитический смысл
дифференциала. Отсюда следует, что при
достаточно малых приращениях аргумента
величина приращения функции приближённо
равна дифференциалу этой функции
f df
10.
Геометрический смысл дифференциалаУчасток СВ - дифференциал df функции f
в точке х
11.
Применение дифференциала для приближенных вычислений.Оно основывается на приближённой формуле : Δf=f’(x)Δx
или f(x+Δx)-f(x)=f’(x)Δx.
Отсюда мы можем вычислить значение функции в точке
x+Δx: f(x+Δx)=f(x)+f’(x)Δx,
если f(х) и f’(x) можно легко вычислить в точке x.
f (b) f (a) f (c)(b a)
12.
f (b) f (a) f (c)(b a)13.
• Применение производной при исследовании функции• Теорема о признаке возрастания и убывания функции.
Если производная функции положительна на некотором
интервале, то функция возрастает на этом интервале,
наоборот если производная отрицательна, то функция
убывает на этом интервале. Производная
дифференцируемой функции в точке экстремума равна
нулю.
14.
Порядок действий приисследовании функции.
1. Найти область определения
функции.
2.Найти производную функции и
определить точки, в которых
производная не существует.
3.Приравнять производную к нулю и
решить полученное уравнение
f (x) 0
15.
Корни этого уравнения являютсяэкстремумами функции.
4. Найти критические точки функции,
как совокупность всех экстремумов и
точек, в которых производная не
существует и отметить их на оси ОХ.
5.Определить знаки производных на
интервалах, на которые критические
точки делят область определения
функции.
16.
6.По знаку производной найти интервалывозрастания и убывания функции.
7. Найти точки экстремумов функции.
17.
Первообразная функцияФункция F(x) называется первообразной функцией функции f(x) на
отрезке [a, b], если в любой точке этого отрезка верно равенство:
F (x) = f(x).
Надо отметить, что первообразных для одной и той же
функции может быть бесконечно много. Они будут отличаться друг
от друга на некоторое постоянное число. F (x) F (x) C
1
2
Неопределенным интегралом функции f(x) называется вся
совокупность первообразных функций F(x), которые
определены соотношением:
f ( x)dx F ( x) C ;
18.
n 1x
x dx n 1 C, n 1
x
a
a dx ln a C
n
e
dx
e
C
x
x
dx
x ln x C
x
1
cos2 x dx tg x C
1
sin 2 x dx ctg x c
cos xdx sinx C
sin xdx cosx C
tgxdx ln cos x C
dx
1 x 2 arctgx C
dx
arcsin x C
1 x2
ctgxdx ln sin x C
19.
Свойства интегралов:1. f ( x)dx ( F ( x) C ) f ( x);
2.d
f ( x)dx f ( x)dx;
3. dF ( x) F ( x) C;
4. (u v w)dx udx vdx wdx;
где u, v, w – некоторые функции от х.
5. C f ( x)dx C f ( x)dx;
20.
Методы интегрированияА) Непосредственное интегрирование.
1
1
2
1
5
1
5
1
cos
x
dx
dx
dx cos xdx 5 x
ln x sinx C 10 x
x 2x
1
2x
x
1 2
1
ln x sinx C
2
2
f (x)dx f (t) (t)dt
Б) Способ подстановки (замены переменных).
sinx cos xdx Сделаем замену
1
2
t 3sin x; dt cos
xdx
3
2
2 2
t C sin 2 x C
3
3
Способ основан на формуле: udv uv vdu
sinx cos xdx t dt t dt
В) Интегрирование по частям
u x 2 ;du 2xdx
x 2 cos x cos x 2xdx x 2 cos x 2 x cos xdx
x
sin
xdx
dv sin xdx; v cos x
2
u x;du dx
x 2 cos x 2 x sin x sin xdx
dv cos xdx; v sin x
u x;du dx
C
x 2 cos x 2 x sin x cos x
dv cos xdx; v sin x
C
21.
Определенный интеграл• Пусть на отрезке [ab] задана непрерывная
функция y=f(x)
22.
Внутри каждого отрезка выберем некоторую точку .x0 < 1 < x1, x1 < < x2, … , xn-1 < n < xn.
Найдем значения функции в этих точках и составим
выражение, которое называется интегральной суммой
для функции f(x) на отрезке [a, b].
2
n
Sn = f( 1) x1 + f( 2) x2 + … + f( n) xn =
f ( ) x
i 1
i
i
Определение: Если при любых разбиениях отрезка
[a, b] таких, что max xi 0 иn произвольном выборе
точек i интегральная сумма S n f ( i ) xi
i 1
стремится к пределу S, который называется опредеb
ленным интегралом от f(x) на отрезке [a, b]: f
a
( x )dx
23.
Определение: Если при любых разбиениях отрезка [a, b] таких,что max xi n0 и произвольном выборе точек i интегральная
сумма S
f ( i ) xi стремится к пределу S, который называется
n
i 1
определенным интегралом от f(x) на
b
отрезке [a, b]:
Свойства определенного интеграла.
b
b
a
a
f ( x)dx
a
a
1) Af ( x)dx A f ( x)dx 2) f ( x) dx 0
b
b
a
b
3) ( f1 ( x) f 2 ( x))dx f1 ( x)dx f 2 ( x)dx
a
a
a
4) Если f(x) (x) на отрезке [a, b] a < b, то
5. Для произвольных чисел a, b, c справедливо равенство:
b
c
c
a
b
a
f ( x)dx f ( x)dx f ( x)dx
b
b
a
a
f ( x)dx ( x)dx
Теорема: (Теорема Ньютона – Лейбница)
Если функция F(x) – какая- либо
первообразная от непрерывной функции
f(x), то b
a
f ( x)dx F (b) F (a) = F(x) ba
24.
25.
26.
27.
Дифференциальное уравнение первого порядка имеет видF(x , y, y′) = 0 .
Если это уравнение разрешено относительно y′ , то это
уравнение имеет вид: y′ = f (x , y) или dy=f (x , y)dx
Общим решением уравнения будет функция y=y(x ,C),
зависящая от х и от одной произвольной постоянной, и
обращающая это уравнение в тождество.
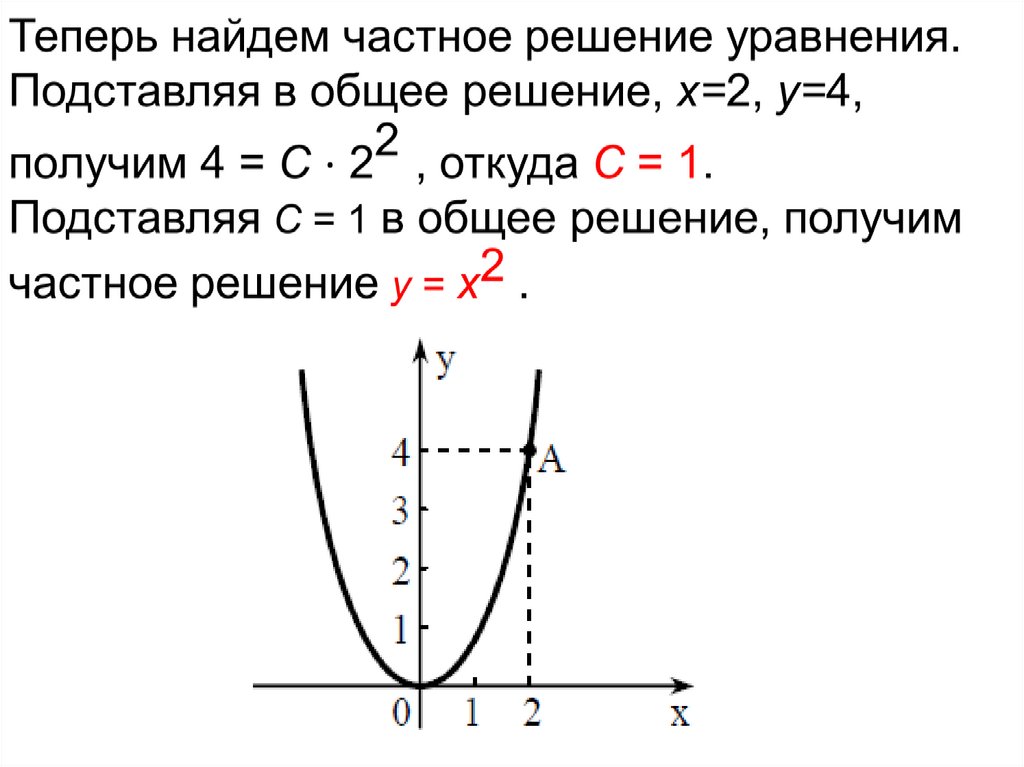
Частным решением уравнения будет решение y= y( x ,C0 ),
полученное из общего при фиксированном значении С,
удовлетворяющее заданным начальным условиям: y = y0 при
x = x0. Другими словами: найти интегральную кривую
уравнения, проходящую через заданную точку M0 (x0,y0 ).
Дифференциальное уравнение вида
P1 (x)Q1(y)dx+P2(x)Q 2 (y) dy =0,
где P1 (x ), P2 (x ) – функции только от х, а Q1(y), Q2(y) –
функции только от у, называется уравнением с
разделяющимися переменными.
28.
Делением обеих частей уравнения на произведение Q1 (y)P2 (x ) можетбыть приведено к уравнению с разделенными переменными:
Общим интегралом уравнения будет:
xy 2y 0
Пример. Дано уравнение
Найти частное решение этого уравнения, удовлетворяющее начальному
условию y = 4 при x = 2 . Уравнение имеет вид: x dy 2y 0
dx
Разделяя переменные, получим: dy 2dx 0
Интегрируем:
y
x
ln y 2ln x C1 ln C
dy
2dx
y x C1
ln y 2ln x ln C
ln y ln Cx
2
y Cx
2
Это общее решение
















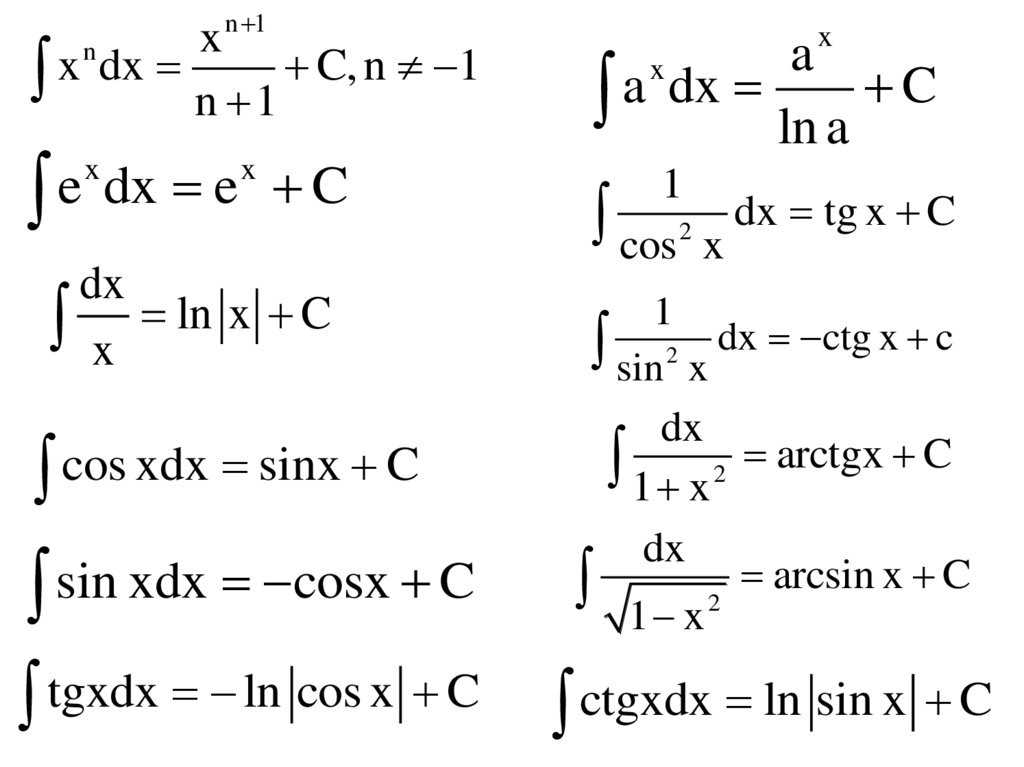










 mathematics
mathematics








