Similar presentations:
Производная функции. Понятие производной
1.
Производная функции.2.
1Понятие производной
2
Геометрический смысл производной
3
Понятие дифференциала
4
Геометрический смысл и
свойства дифференциала
3.
Понятие производнойПусть функция y = f ( x ) определена в некоторой окрестности точки x0 .
Предел отношения приращения y функции в этой точке (если он
существует) к приращению x аргумента, когда x 0 , называется
производной функции f ( x ) в точке x0 .
df ( x0 )
′
Обозначения: f ( x ) или y ( x0 ) или
или f x= x 0 .
dx
Таким образом,
f ( x0 x)
y f ( x0 ) lim
x
x→0
f ( x0 )
Вычисление производной называется дифференцированием функции.
4.
Таблица производных1.
(c) 0, c const
2.
( x ) x 1 (где ); в частости, ( x )
3.
(a x ) a x ln a, a 0 ,в частности, (e x ) e x ;
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
16.
1
2 x
;
1
1
, a 0, a 1 ;в частности, (ln x) ;
x ln a
x
(sin x) cos x ;
(cos x) sin x ;
1
;
(tgx)
cos 2 x
1
;
(ctgx)
sin 2 x
1
;
(arcsin x)
2
1 x
1
;
(arccos x)
2
1 x
1
;
( arctgx)
1 x2
1
;
( arcctgx)
1 x2
( shx) chx ;
(chx) shx ;
1
(thx) 2 ;
ch x
1
(cthx) 2 ;
sh x
(log a x)
5.
Основные правила дифференцированияПусть c – константа, а u( x ) и v( x ) имеют производные в
некоторой точке x . Тогда функции u( x ) ± v( x ) , c u (x) , u ( x) v( x) и
u( x )
(где v( x ) ≠ 0 ) также имеют производные в этой точке, причем
v( x )
1.
2.
( u ± v )′ = u′ ± v′ ;
(u v) u v uv , в частности, (cu) c u ;
cv
u u v uv
c
.
, в частности,
3.
2
2
v
v
v
v
Пусть теперь функция u = φ( x ) имеет производную в точке x 0 ,
функция y = f ( u ) – в точке u0 = φ( x0 ) . Тогда сложная функция y = f ( φ( x ))
также имеет производную в точке x 0 , причем
y ( x0 ) y (u0 ) u ( x0 ) .
6.
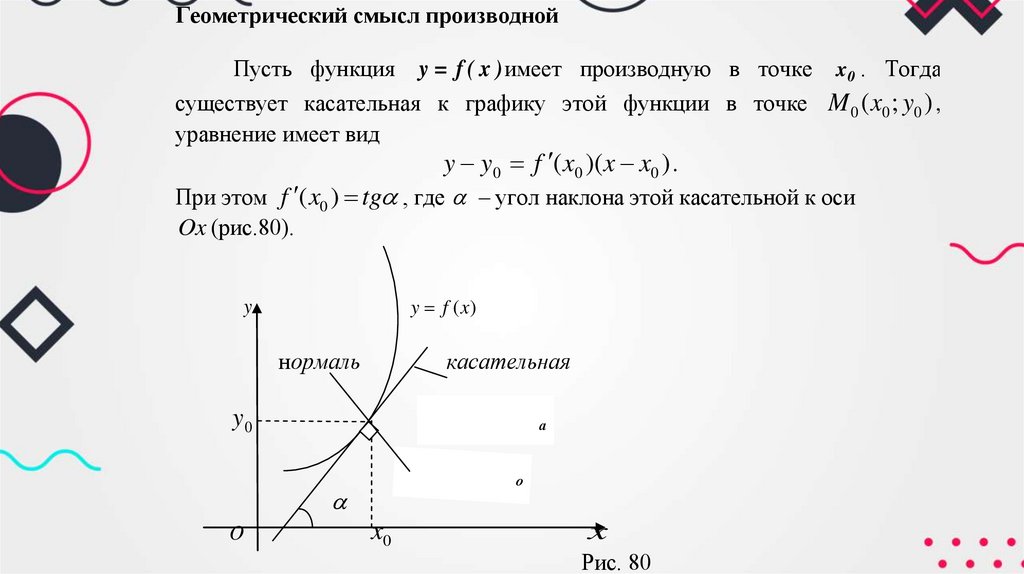
Геометрический смысл производнойПусть функция y = f ( x ) имеет производную в точке x 0 . Тогда
существует касательная к графику этой функции в точке M 0 ( x0 ; y0 ) ,
уравнение имеет вид
y y0 f ( x0 )(x x0 ) .
При этом f ( x0 ) tg , где – угол наклона этой касательной к оси
Ox (рис.80).
y f (x)
y
нормаль
касательная
y0
O
x0
а
с
а
т н
о е
р л
м ь
а н
л а
ь я
к
x
Рис. 80
7.
Прямая, проходящая через точку касания, перпендикулярно касательной,называется нормалью к кривой имеет уравнение
1
y y0
( x x0 ) .
f ( x0 )
Если f ( x0 ) = 0 (т.е. касательная горизонтальна), то нормаль
вертикальна имеет уравнение x x0 .
Пусть даны две пересекающиеся в точке M 0 ( x0 , y0 ) кривые y = f 1 ( x ) и
y = f 2 ( x ) , причем обе функции имеют производные в точке x0 . Тогда
углом мeжду этими кривыми называется угол между касательными к
ним, проведенными в точке M 0 .
Этот угол можно найти из формулы
tg
f '2 ( x0 ) f '1 ( x0 )
1 f '1 ( x0 ) f '2 ( x0 )
8.
Логарифмическая производнаяПри нахождении производных от показательно-степенной функции
u ( x) v ( x ) , а также других громоздких выражений, допускающих
логарифмирование (произведение, частное и извлечение корня), удобно
применять логарифмическую производную.
Логарифмической производной от функции
производная от логарифма этой функции:
y
ln y .
y
y = f ( x ) называется
Используя логарифмическую производную, нетрудно вывести
v( x)
формулу для производной показательно-степенной функции u ( x ) :
(u v )' u v v' ln u u v 1 u ' v
9.
Производная неявной функцииПусть функция y = y( x ) , обладающая производной в точке x , задана неявно
уравнением
F ( x, y ) 0 .
(1.1)
Тогда производную y' ( x ) этой функции можно найти, продифференцировав
уравнение (1.1) (при этом у считается функцией от x ) и разрешая затем
полученное уравнение относительно y' .
10.
Производные высших порядковПроизводная f ' ( x ) от функции f ( x ) называется также производной первого
порядка. В свою очередь производная от функции f ' ( x ) называется
производной второго порядка от функции f ( x ) (или второй производной) и
обозначается f '' ( x ) .
Аналогично определяются производная третьего порядка (или третья
производная), обозначаемая f (x) и т.д.
Производная n-го порядка обозначается f
n
(x) .
11.
Производная функций, заданных параметрическиПусть функция y = f ( x ) определена параметрическими функциями x x(t )
и y y (t ) . Тогда если функции x (t ) и y (t ) имеют производные в точке t 0 ,
причем x' (t0 ) ≠ 0, а функция y = f ( x ) имеет производную в точке
x0 x(t0 ) , то эта производная находится по формуле
y 't (t 0 )
y ' ( x0 )
x't (t 0 )
или
yt
y' x .
xt
Вторая производная y' ' ( x ) находится по формуле
y ' 't xt ' x' 't y 't
y ' ' xx
( x 't ) 3
12.
Пример1.1.Пользуясь
определением,
найти
производную
функции
y = f ( x ):
Пример 1.1 (1) y 3x 2 ;
Решение. Придадим аргументу x приращение Δx . Тогда соответствующее
приращение Δy функции будет иметь вид
y f ( x x) f ( x) 3( x x) 2 3x 2 3( x 2 2 x x ( x) 2 x 2 ) 3 x(2 x x)
Отсюда находим предел соотношения
lim
Δy
в точке x при Δx → 0 :
Δx
y
3 x(2 x x)
lim
lim
3 lim (2 x x) 3 2 x 6 x.
x 0 x
x 0
x 0
x
Таким образом, y' = ( 3 x 2 )' = 6 x .
13.
Пример 1.1 (2) y sin x.Решение. Найдем приращение Δy функции, соответствующее
приращению Δx аргумента, используя формулу разности синусов:
x
x
y sin( x x) sin x 2 sin cos( x )
2
2
Отсюда
x
x
x
cos x
sin
y
2
2
2 lim cos x x cos x.
lim
lim
lim
x 0 x
x 0
x 0 x x 0
x
2
2
В последнем равенстве мы воспользовались первым замечательным
пределом и непрерывностью cos x . Таким образом, y ' (sin x)' cos x .
2 sin
14.
Пример 1.2.Пользуясь
найти f ' ( x) , если:
Пример 1.2 (1) f ( x )
9
3
x2
основными
правилами
дифференцирования,
5 x 1 ;
Решение. Преобразуем функцию к виду
f ' ( x) 9 x 2 / 3 5 5 x .
Отсюда, используя таблицу производных, получим
f ' ( x) (9 x 2 / 3 5 5 x )' (9 x 2 / 3 )' (5 5 x )'
9 x
2 / 3
2 3 1
x
5 (5 )' 9 3 x 5 5 x ln 5 6 x 5 / 3 5 x 1 ln 5
2
15.
Пример 1.2 (2) f ( x) ( x 4 x) (3tgx 1) .Решение. Воспользуемся формулой для производной произведения:
f ' ( x) [( x 4 x)(3tgx 1)]' ( x 4 x)' (3tgx 1) ( x 4 x)(3tgx 1)'
(4 x 3 1)(3tgx 1) ( x 4 x)
3
cos 2 x
Пример 1.3. Применяя правило дифференцирования сложной функции,
найти производную функции
Пример 1.3 (1) y sin x.
2
Решение. Данная функция является композицией двух имеющих
производные функций u sin x и
f (u ) u 2 . Так как u ' cos x , а
f ' (u ) 2u , то с учетом правила дифференцирования сложной функции
получим:
y ' ( x) (u 2 )' x 2u u ' 2 sin x cos x sin 2 x .
16.
Пример 1.3 (2) y ln( arctg3x)Решение. Функция ln(arctg 3) — композиция функций
u arctg 3 x и f (u ) ln u , откуда
y ' ( x) (ln u )' x
1
1
u'
(arctg3x)' .
u
arctg3x
Функция arctg3 x , в свою очередь, является композицией двух функций
v 3 x и g (v) arctgv , поэтому для нахождения ее производной нам
придется еще раз применить правило дифференцирования сложной
функции:
1
1
3
(arctg3 x)' (arctgv)' x
v'
3
.
2
2
2
1 v
1 (3 x)
1 9x
Отсюда
y'
1
3
(arctg 3 x)'
.
2
arctg 3 x
(1 9 x )arctg 3 x
окончательно
17.
Пример. 1.4. Используяпроизводные функций:
логарифмическую
производную,
найти
Пример. 1.4 (1) y x sin x
Решение: Прологарифмируем обе части равенства y x
ln y ln x sin x ,
т.е.
ln y sin x ln x .
Теперь
sin x
. Тогда
продифференцируем
последнее равенство, при этом в левой части используем производную
сложной функции, а в правой
– производную произведения:
(ln y ) (sin x ln x) ,
т.е.
y
(sin x) ln x sin x(ln x)
y
y
sin x
cos x ln x
.
y
x
sin x
или, учитывая, что y x sin x ,
x
sin x
y x sin x (cos x ln x
).
x
Отсюда y y (cos x ln x
или
18.
Пример. 1.4 (2) y( x 1) 3
x 2
( x 1) 2
3
Решение. Непосредственное дифференцирование данной дроби
привело
бы
к
громоздким
вычислениям,
зато
применение
логарифмической производной позволяет найти ответ без труда:
ln y ln
( x 1) ( x 2)
3
( x 1)
1
2
2
3
Отсюда, используя формулы для логарифма произведения, частного и
степени, получим:
1
2
2
3
ln y ln( x 1) ln( x 2) ln( x 1) ,
3
т.е.
1
2
ln( x 2) ln( x 1)
2
3
Осталось продифференцировать обе части полученного равенства:
1
2
(ln y ) [3 ln( x 1) ln( x 2) ln( x 1)]
2
3
Или
y
3
1
2
,
y
x 1 2( x 2) 3( x 1)
Откуда
3
1
2
,
y y
x
1
2
(
x
2
)
3
(
x
1
)
Т.е.
ln y 3 ln( x 1)
y
3
x 2 3
1
2
x 1 2( x 2) 3( x 1)
.
3
( x 1) 2
( x 1)
19.
Пример 1.5. Найти производную неявно заданной функции y :x 3 y 3 sin( x 2 y )
Решение. Дифференцируя обе части уравнения и учитывая, что
есть функция от x (поэтому, например, ( y 3 )' x 3 y 2 y ' ), получим:
3x 2 3 y 2 y ' cos( x 2 y )(1 2 y ' )
или
3x 2 3 y 2 y' cos( x 2 y) 2 y' cos( x 2 y) .
Отсюда находим y' :
3 y 2 y ' 2 y ' cos( x 2 y ) cos( x 2 y ) 3x 2
Или
y ' (3 y 2 2 cos( x 2 y )) cos( x 2 y ) 3x 2 ,
Т.е.
cos( x 2 y ) 3 x 2
y' 2
.
3 y 2 cos( x 2 y )
y —
20.
Пример 1.6. Найти производную y' (x) от следующей функции, заданнойx 2 cos t ,
параметрически:
y 3 sin t.
Решение. Производная функции y(x) находится по формуле y' (x)
откуда в нашем случае
(3 sin t )'t
3 cos t
y ' ( x)
1,5ctgt .
(2 cos t )'t
2 sin t
y' (t)
,
x' (t)
21.
Пример. 1.7 (1) Написать уравнения касательной и нормали к параболеy 2 4x в точке M(1;2).
Решение. Найдем y' (x)
как
производную
неявной
функции:
2
y
(y 2 )' (4x)' , т. е. 2yy' 4 , откуда y' . Значит, y' (x0 ) y' (1) 1 .
Отсюда получаем уравнение касательной в точке М:
y 2 x 1 , т.е. y x 1 .
Теперь найдем уравнение нормали:
y 2 ( x 1), т.е. y x 3
Пример. 1.7 (2) Найти точки, в которых касательная к графику
гиперболы y
1
1
параллельна прямой y x 3
x
4
1
4
Решение. Угловой коэффициент данной прямой равен ,
поэтому
1
4
производная к кривой в искомой точке x 0 также равна :
y' (x0 )
1
4
,
x 2 4, или x 2 .
т.е.
1
1
,
2
4
x
откуда
22.
8Пример. 1.7 (З) Найти угол, под которым пересекаются кривые: y
x
x 2 y 2 12 .
Решение. Сначала найдем точку пересечения кривых, для чего подставим
2
8
8
2
y во второе уравнение: x 12 , или
x
x
64
t
12 , где t x 2 . Решая последнее уравнение, найдем t 16 ,
t
откуда x 4, y 2 . Таким образом, имеем 2 точки пересечения M1 (4;2)
и M 2 ( 4; 2) .
Найдем угол φ1 пересечения кривых в точке M1 , предварительно
вычислив y1 (4) и y 2 (4) из уравнений y
8
и x 2 y 2 2 12 :
x
и
23.
88
y1 2 y1 (4) 0,5 ;
16
x
2
x 2 y2 12 2 x 2 y2 y2 0
x
4
y 2
y 2 ( 4) 2 .
y2
2
Теперь окончательно найдем
1
1
2
2
y 2 ( 4) y1 ( 4)
2
2.
tg 1 tg 1
1 y1 (4) y 2 ( 4) 1 1 1 1
Поскольку знаменатель дроби обратился в ноль, то это означает, что
π
φ1 .
2
π
Аналогично находим угол φ2
во второй точке пересечения
2
данных кривых.
24.
Пример 1.8 (1) Найти f (x), где f ( x) sin 3xРешение. Находим первую производную:
f ( x) (sin 3x) 3 cos 3x .
Отсюда получим вторую производную –
f ( x) (3 cos 3x) 9 sin 3x ,
А затем и искомую третью:
f ( x) ( 9 sin 3x) 27 cos 3x
Пример 1.8 (2) Найти y xx
параметрически x t 2 , y t 3
для
функции
y y(x),
заданной
Решение. Воспользуемся формулой
откуда
xt ytt yt xtt
y xx
,
3
( xt )
(t 2 ) (t 3 ) (t 3 ) (t 2 ) 2t 6t 3t 2 2 6t 2 3
y xx
3 .
2
3
3
4t
[(t ) ]
(2t )
8t
25.
ДИФФЕРЕНЦИАЛПонятие дифференциала
Пусть функция y f(x) определена в некоторой окрестности точки x0 .
Тогда если существует такое число A , что приращение Δy этой функции
в точке x0 , соответствующее приращению Δx аргумента, представимо в
виде:
y A x ( x) x ,
(2.1)
где lim α(Δx) 0, то функция называется дифференцируемой в точке x0 .
Δx 0
При этом главная, линейная относительно Δx , часть этого приращения, т. е.
A Δx , называется дифференциалом функции в точке x 0 и обозначается
dy или df(x0 ) .
Нетрудно показать (положив y x в формуле (2.1)), что dx Δx .
Функция f(x) дифференцируема в точке хо тогда и только тогда, когда в
этой точке существует конечная производная f' (x0 ) ; при этом A f' (x0 ) .
Поэтому df(x0 ) f' (x0 )dx , или, если f' (x) существует на данном
интервале (a;b) , то dy f' (x)dx , x a, b .
26.
Отсюда f' (x)dy
, т. е. производная функции y f(x) в точке x
dx
равна отношению дифференциала этой функции в данной точке к
дифференциалу независимой переменной.
Если приращение Δx аргумента x близко к нулю (т. е. достаточно
мало), то приращение y функции приближенно равно ее дифференциалу,
т.е. Δy dy , откуда
f ( xo x) f ( x0 ) f ' ( x0 ) x
df ( x0 )
Последняя формула удобна для приближенного вычисления значения
функции f (x ) в точке x0 x по известному значению этой функции и
ее производной в точке x0 .
27.
Геометрический смысл и свойства дифференциалаГеометрически приращение Δy функции f(x) в точке x – есть
приращение ординаты точки на кривой ( Δy AC ), а дифференциал dy
функции в этой точке – приращение ординаты соответствующей точки на
касательной ( dy AB) .
y f (x)
..
. .
. x.
y
x
x x
x
28.
Пусть u(x) и v(x) – некоторые функции, дифференцируемые в точке x .Тогда:
1.
dC 0 ,где С – константа.
d ( u ) du, где – константа.
2.
3.
4.
5.
d (u v) du dv .
d (u v) udv vdu .
u vdu udv
d
.
2
v
v
6.
Инвариантность формы дифференциала. Если y f(u(x)) – сложная
функция, то
df (u ) f (u )dv, или dy yu du ,
т.е. форма дифференциала не меняется (инвариантна) независимо от того,
рассматривается y как функция независимой переменной x или зависимой
переменной u .
29.
Дифференциалы высших порядковПусть функция y f(x) дифференцируема на интервале (a,b).Тогда, как
известно, в каждой точке этого интервала определен дифференциал
dy f (x)dx функции f(x), называемый также дифференциалом первого
порядка (или первым дифференциалом).
Дифференциалом второго порядка (или вторым дифференциалом) от
функции y f(x) в точке x (a,b) называется дифференциал от
дифференциала первого порядка функции f(x) в этой точке.
Дифференциал второго порядка обозначается d 2 y или d 2 f(x) .
Таким образом, d 2 y d(dy) . Учитывая, что dy f' (x)dx , где dx — не
зависящая от x константа, получим
d 2 y f'' (x)(dx)2 , или, более кратко, d 2 y f'' (x)dx2
30.
Аналогично определяются дифференциалы третьего и болеевысоких порядков: d 3 y d(d 2 y) , d 4 y d(d 3 y) , В общем случае,
дифференциалом n-го порядка от функции f(x) в точке x называется
дифференциал от дифференциала (n — 1)-го порядка функции f(x) в
этой точке:
d n y d(d n 1 y) , т. е. d n y f (n) (x)(dx)n , или, более кратко,
d n y f n (x)dxn . Отсюда следует, что
f
(n)
(x)
dny
dx n
d2y
, в частности f'' (x) 2
dx
Заметим, что lkz дифференциалов высших порядков
свойство инвариантности (как для дифференциалов первого
порядка) не имеет места.
31.
Пример. 1.9. Найти дифференциал функции y ex3
Решение. Так как dy y' dx , то в данном случае dy (e
x3
3
3
)' dx 3x e dx .
2
x
3
Так как dy y' dx , то в данном случае dy (e x )' dx 3x 2 e x dx .
Пример. 1.10. Найти приращение и дифференциал функции y x 2 3x 1 в
точке x0 2 , если Δx 0,1 .
Решение. Сначала найдем приращение Δy в общем виде:
y y ( x x) y ( x) [( x x) 2 3( x x) 1] ( x 2 3 x 1)
x 2 2 x x ( x) 2 3 x 3 x 1 x 2 3 x 1
2 x x 3 x ( x) 2 (2 x 3) x ( x) 2
.
32.
Из полученного выражения для приращения Δy видно, что еголинейная часть в произвольной точке x 0 равна 2x0 3 x . Тогда по
определению данной функции будет равен dy (2x 3) x , или, в
привычной записи, dy (2x 3)dx .
Второе слагаемое в полученной записи для Δy , т.е. Δx , есть
бесконечно малая более высокого порядка, чем первое слагаемое.
Заметим, что можно найти dy и сразу (без вычисления Δy ) по
2
2
формуле dy y' dx , откуда dy (x 3x 1)' dx (2x 3)dx .
Теперь найдем Δy и dy в точке x 0 2 , если Δx 0,1 :
y (2 2 3) 0,1 (0,1) 2 0,1 0,01 0,11, dy 0,1 .
33.
Пример. 1.11 (1). Вычислить приближенно: ln1,02Решение. Воспользуемся приближенной формулой
f(x0 Δx) f(x0 ) f (x0 ) x .
Тогда, подставляя f(x) lnx, получим
1
ln( x0 x ) ln x0 x .
x0
Полагая здесь x0 1, Δx 0,02, найдем
1
ln 1,02 ln 1 0,02 0,02 .
1
Таким образом, ln1,02 0,02 .
34.
Пример. 1.11 (2) Вычислить приближенно: 24 .Решение: Учитывая, что f(x) x , x 0 25, Δx 1 , получим
1
x x x0
x , т.е.
2 x0
1
24 25
( 1) 4,9
2 25
Окончательно 24 4,9
2
Пример. 1.12. Найти dy, d y и d 3 y для функции y 3 x .
Решение. Поскольку
dy y dx (3 x ) dx
1 2 / 3
dx
,
x dx
2
3
3
3 x
35.
То2
dx
1
1
2
2
dx
(dx) 2 ( x 2 / 3 ) dx x 5 / 3 dx 2
d 2 y d (dy ) d
2
2
3
3
3
9
9 x3 x 2
3 x 3 x
.
Отсюда
2
3
2
dx
2
10
10
dx
5 / 3
3
8 / 3
3
.
d 3 y d (d 2 y ) d
(
x
)
dx
x
dx
5/3
2
2
3
9
27
27 x
9x
То же самое можно было найти иначе, предварительно отыскав
производные y , y и y , а затем воспользоваться формулами:
d 2 y y dx 2 , d 3 y y dx 3 .



































 mathematics
mathematics








