Similar presentations:
Дифференциальное исчисление функции одной переменной. Производная функции в точке
1.
Дифференциальное исчисление функции однойпеременной. Производная функции в точке.
Дифференциал.
1. Производная функции в точке.
2. Геометрический и механический смыслы производной.
3. Дифференцирование сложных функций.
4. Дифференциал функции, свойства, приложения.
5. Производные и дифференциалы высших порядков.
2.
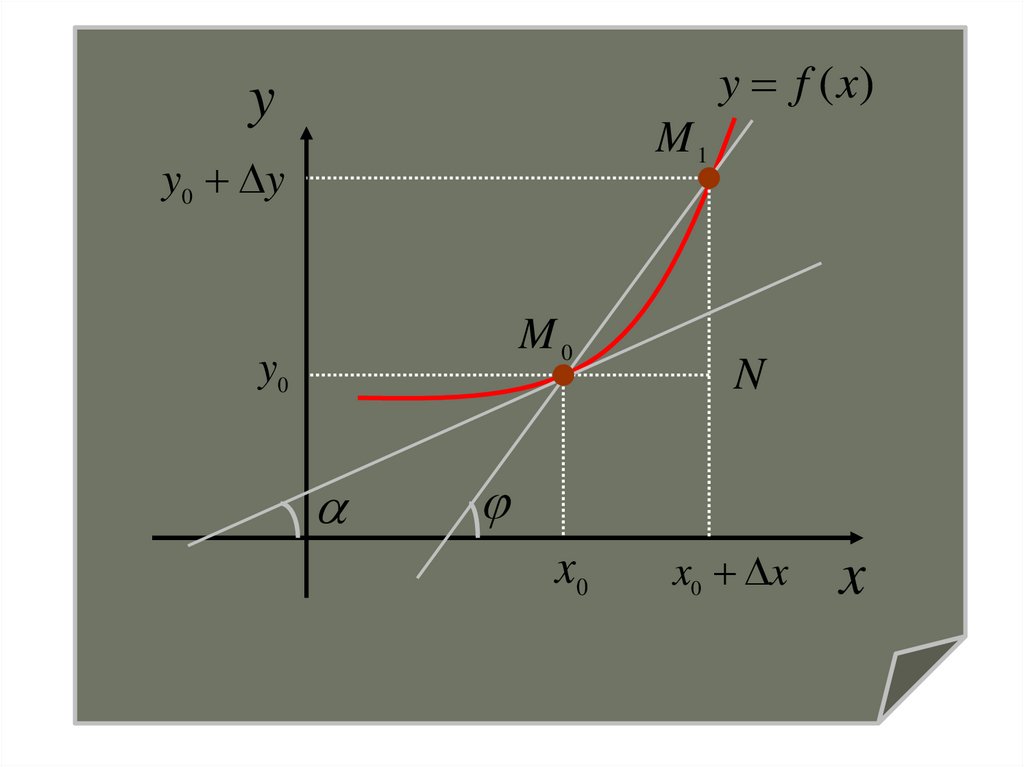
1. Задача о касательнойПусть на плоскости XOY задана непрерывная
кривая y=f(x).
Необходимо найти уравнение касательной к этой
кривой в точке M0(x0,y0).
3.
Дадим аргументу x0 приращение Δx и перейдем накривой от точки M0(x0, f(x0)) к точке M1(x0+Δx,
f(x0+ Δx)).
Проведем секущую M0M1.
Под касательной к кривой y=f(x) в точке
M0 (x0 ,y0 ) понимают предельное положение
секущей M0 M1 при приближении точки M1
x
0
к точке M0 , т.е. при
4.
y f (x)y
M1
y0 y
M0
y0
N
x0
x0 x
x
5.
Уравнение прямой, проходящей через точку M0имеет вид:
y f ( x0 ) k ( x x0 )
Рассмотрим прямоугольный треугольник M0M1N:
kM
0 M1
y
tg
x
- угловой коэффициент секущей M0M1.
6.
Тогда угловой коэффициент касательной ккривой в точке M0 :
k lim kM M
x 0
0
1
y
lim
x 0
x
7.
2. Задача о скоростидвижения
Пусть вдоль некоторой прямой движется точка
по закону S=S(t), где S – пройденный путь, t –
время движения.
Требуется найти скорость в момент времени t0 .
8.
На момент времени t0 пройденный путь составитS0=S(t0), на момент времени t0+Δt пройденный
путь составит S0+ΔS=S(t0 +Δt ).
Тогда за промежуток
скорость составит:
времени Δt средняя
S
vср
t
Чем меньше Δt, тем лучше средняя скорость
характеризует движение в момент t0.
9.
Поэтому под скоростью точки в момент времениt0 понимают:
S
v lim vср lim
t 0
t 0
t
10.
Пусть функция y=f(x) определена на промежутке Х.Выберем точку x X
Дадим аргументу x приращение Δx, тогда функция
получит приращение
Δy=f(x+Δx)- f(x).
11.
Производной функции y=f(x)называется предел отношения
приращения функции к приращению
независимого аргумента, когда
приращение аргумента стремится
к нулю:
y
f ( x x) f ( x)
y lim
lim
x 0 x
x 0
x
12.
Обозначения производной:y ;
f ( x);
dy
;
dx
df ( x)
dx
Нахождение производной функции называется
дифференцированием.
Если функция имеет конечную производную в
некоторой точке, то она называется
дифференцируемой в этой точке.
13.
Вернемся к рассматриваемым задачам.Из задачи о касательной вытекает
Производная f / (x0) есть угловой коэффициент
(тангенс
угла
наклона)
касательной,
проведенной к кривой y=f(x) в точке x0 :
k f ( x0 )
14.
Тогда уравнение касательной к кривой вданной точке будет иметь вид:
y f ( x0 ) f ( x0 ) ( x x0 )
15.
Из задачи о скорости движения вытекаетПроизводная пути по времени S / (t0)
скорость точки в момент времени t0 :
v(t0 ) S (t0 )
есть
16.
Если функция y=f(x)дифференцируема в точке x0,
то она непрерывна в этой
точке.
17.
Непрерывность функции является необходимым,но не достаточным условием дифференцируемости
функции.
Если функция имеет непрерывную производную на
промежутке Х, то она называется гладкой на
этом промежутке.
Если производная функции имеет конечное число точек
разрыва 1 рода, то такая функция называется
кусочно-гладкой.
18.
Производная функции может быть найдена посхеме:
1
Дадим аргументу х приращение Δх и
найдем значение функции y+Δy=f(x+Δx)
19.
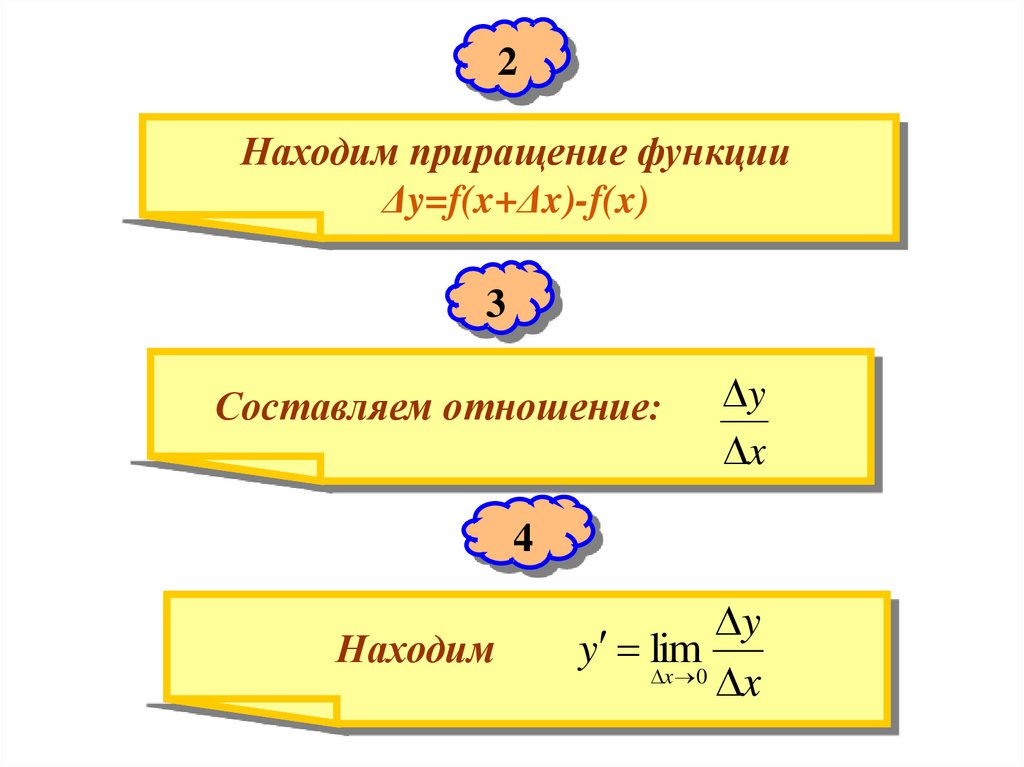
2Находим приращение функции
Δy=f(x+Δx)-f(x)
3
Составляем отношение:
y
x
4
Находим
y
y lim
x 0
x
20.
Найдем производную функции1
y x
Дадим аргументу х приращение Δх и
найдем значение функции y+Δy:
y y ( x x)
2
3
3
Находим приращение функции
y ( x x) x
3
3
21.
x 3 x x 3x x x x3
2
2
3
x(3x 3x x x )
2
3
2
y
Составляем отношение
x
y
2
2
3x 3x x x
x
3
22.
4y
Находим y lim
x 0
x
y lim (3x 3x x x ) 3x
2
2
2
x 0
0
0
Полученный результат является частным
случаем производной от степенной функции
y x
n
Можно показать, что в общем случае
23.
( x ) n xn
n 1
24.
Таблица производных основныхэлементарных функций.
–
1.
–
2.
–
3.
–
4.
–
5.
–
6.
–
7.
–
–
–
(C ) 0
( x ) n x
n
n 1
(a x ) a x ln a
(e x ) e x
( x) 1
( x 2 ) 2 x
x 2 1 x
1
(loga x)
1 x ln a
(ln x)
x
(sin x) cos x
8. (cosx) sin x
1
(
tg
x
)
9.
cos2 x
1
(ctg x) 2
10.
sin x
11.
12.
13.
14.
(arcsin x)
(arccosx)
1
1 x2
1
1 x2
1
1 x2
1
(arcctgx)
1 x2
(arctgx)
25.
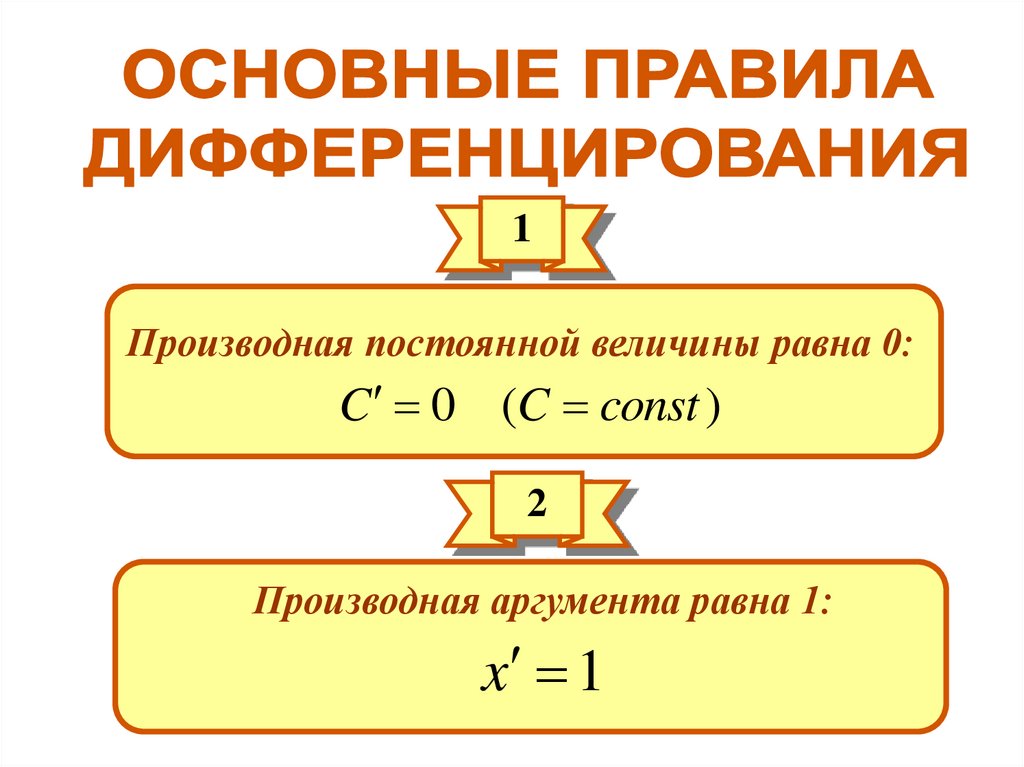
1Производная постоянной величины равна 0:
C 0 (C const )
2
Производная аргумента равна 1:
x 1
26.
3Производная алгебраической суммы
(разности) конечного числа
дифференцируемых функций равна сумме
(разности) производных этих функций:
(u v) u v
27.
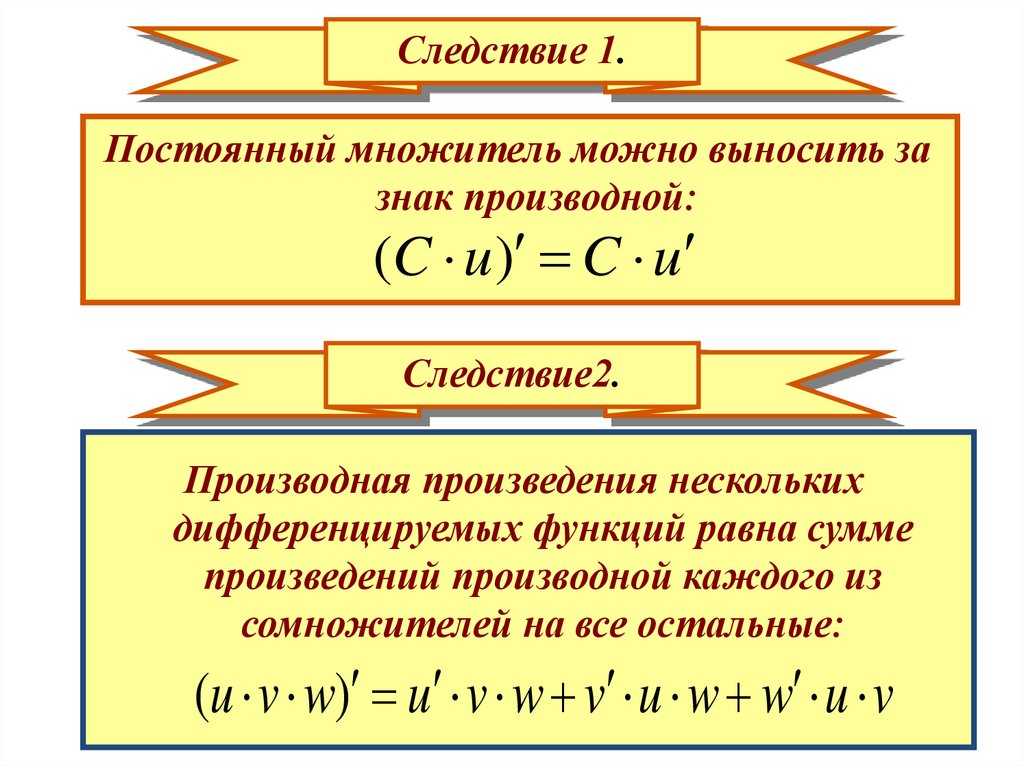
Следствие 1.Постоянный множитель можно выносить за
знак производной:
(C u ) C u
Следствие2.
Производная произведения нескольких
дифференцируемых функций равна сумме
произведений производной каждого из
сомножителей на все остальные:
(u v w) u v w v u w w u v
28.
5Производная частного двух дифференцируемых
функций находится по формуле:
u u v v u
2
v
v
29.
1Найти производную функции
y 15 ( x 1)
4
и вычислить ее значение в точке х=1.
30.
44
y 15 ( x 1) 15 ( x 1)
0
15 (4 x ) 60 x
3
3
Находим значение производной в точке х=1:
y (1) 60 1 60
3
31.
2Найти производную функции
y x ( x 1)
3
4
и вычислить ее значение в точке х=1.
32.
y x3
(
4
x 1) x ( x 1)
3
4
1 3
3x ( x 1) x x
4
2
9
4
4
9
4
3
4
9
4
1
13
3x 3x x x 3x 2
4
4
2
Находим значение производной в точке х=1:
13 94
25
2
y (1)
1 3 1
4
4
33.
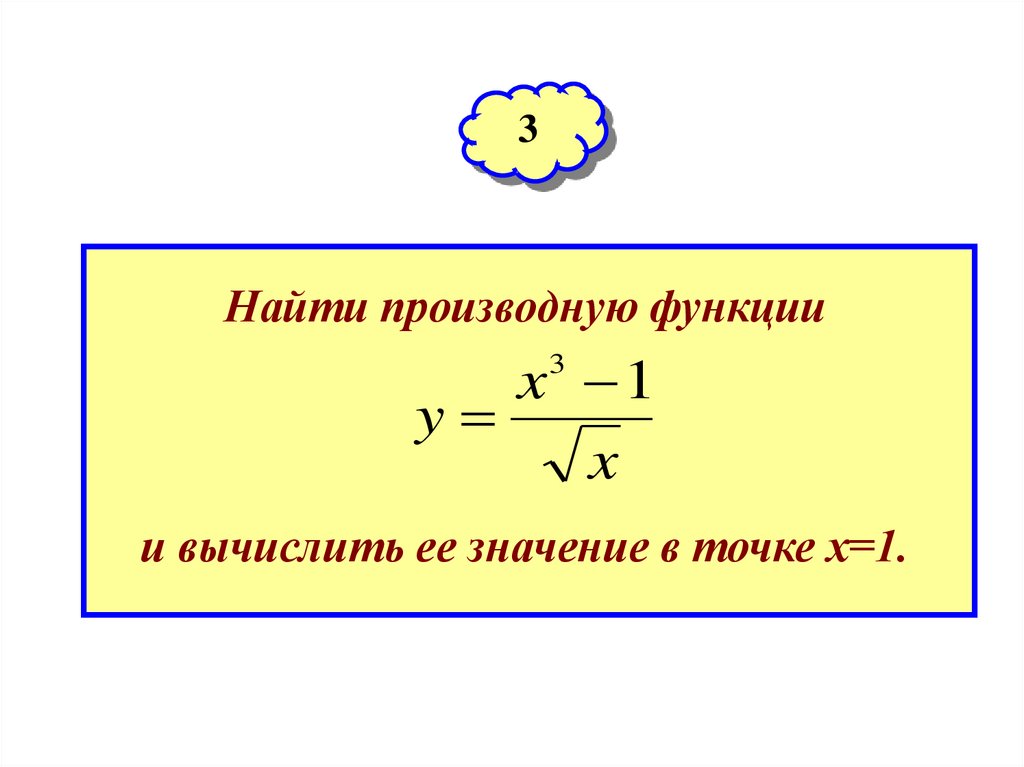
3Найти производную функции
x 1
y
x
3
и вычислить ее значение в точке х=1.
34.
xy
3
1 x ( x 1)
x
3x
2
5
2
3
x
1
1 2
3
x ( x 1) x
2
x
5
2
1
1
3x x x
2
2
x
1
2
5
2
5
1
x x
2
2
x
1
2
Находим значение производной в точке х=1:
5 52 1 12
1 1
2
y (1) 2
3
1
35.
Пусть переменная y есть функция от переменнойu, y=f(u).
И пусть переменная
переменной x, u=φ(x).
u
есть
То есть задана сложная функция
y f (x )
функция
от
36.
Если y=f(u), u=φ(x) – дифференцируемыефункции своих аргументов, то производная
сложной функции существует и равна
производной
данной
функции
по
промежуточному аргументу, умноженной на
производную
самого
промежуточного
аргумента по независимой переменной:
y f (u ) u x
37.
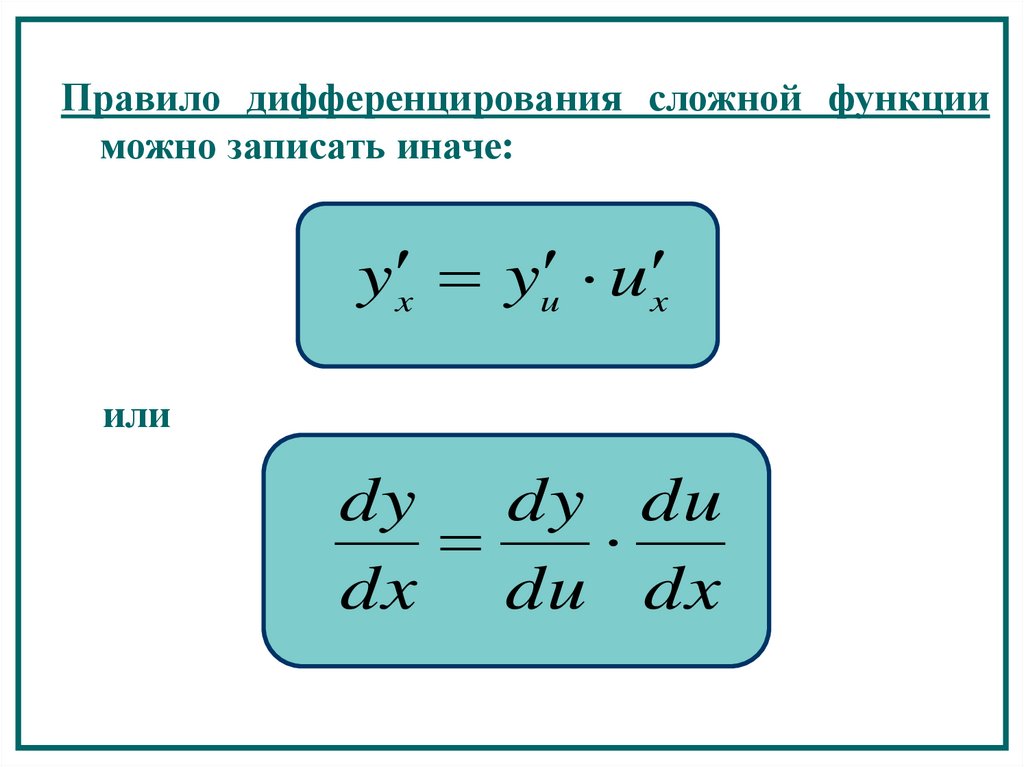
Правило дифференцирования сложной функцииможно записать иначе:
y x yu u x
или
dy dy du
dx du dx
38.
Найти производные сложных функций:1
y
x 5
3
39.
2y 3 x 5 x 5
3
1
x 5 x
2
2
1
2
3
2
1
x 5
x
2
40.
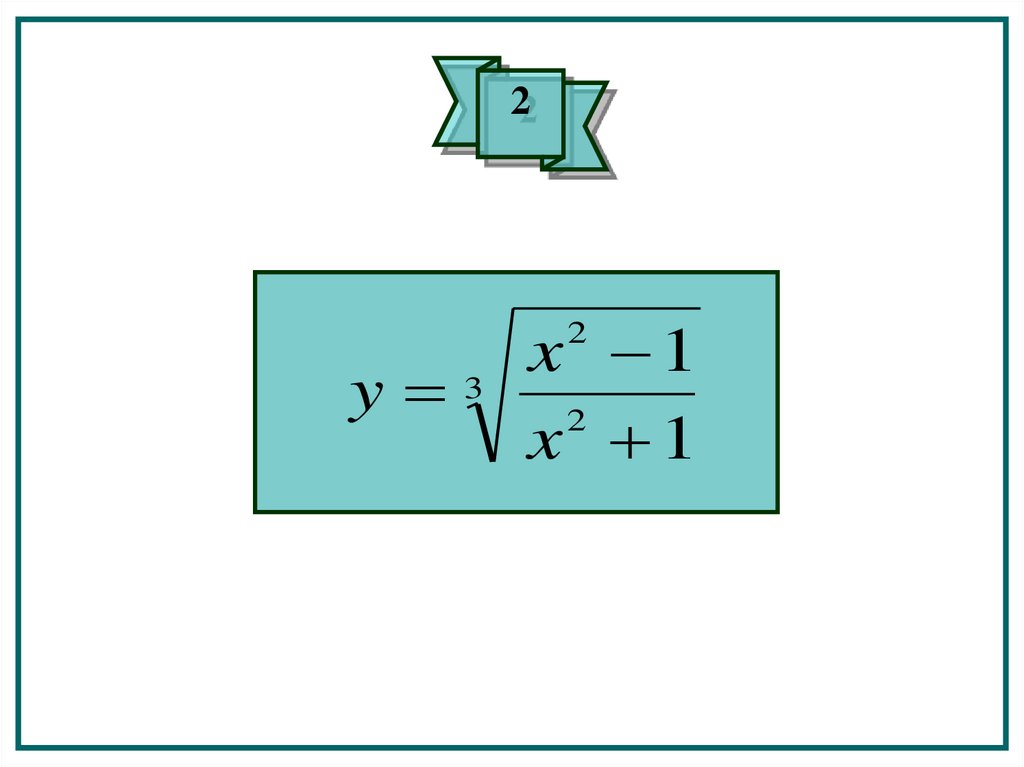
2y 3
x 1
2
x 1
2
41.
1 x 1y 2
3 x 1
2
2
3
2
3
x 1
2
x 1
2
1 x 1 ( x 1) ( x 1) ( x 1) ( x 1)
2
2
2
3 x 1
( x 1)
2
2
2
2
2
42.
23
1 x 1 2 x ( x 1) 2 x ( x 1)
2
2
2
3 x 1
( x 1)
2
1 x2 1
2
3 x 1
2
2
3
2
2 x3 2 x 2 x3 2 x
2
2
( x 1)
2
3
2
1 x 1
4x
2 2
3 x 1 ( x 1) 2
43.
Пусть y=f(x) – дифференцируемая и монотоннаяфункция на промежутке Х.
Если переменную y рассматривать как аргумент,
а переменную x как функцию, то функция x=φ(y)
является
обратной
функцией
к
данной,
непрерывной на соответствующем промежутке Y.
44.
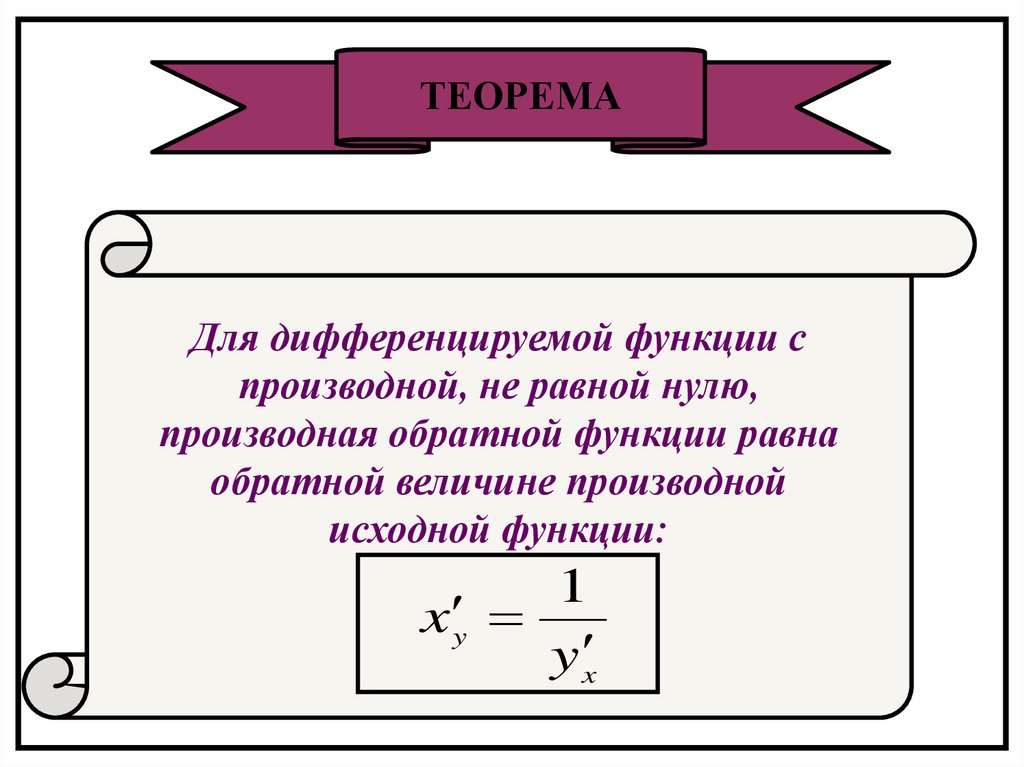
ТЕОРЕМАДля дифференцируемой функции с
производной, не равной нулю,
производная обратной функции равна
обратной величине производной
исходной функции:
1
x y
y x
45.
Пусть функция y=f(x) определена на промежуткеХ и дифференцируема в некоторой окрестности
точки x X
Тогда существует конечная производная
y
lim
f ( x)
x 0
x
На основании теоремы о связи бесконечно
малых величин с пределами функций имеем:
46.
yf ( x) ( x)
x
Где ( x) - бесконечно малая величина при x 0
Следовательно,
y f ( x) x ( x) x
Таким образом, приращение функции y
состоит из двух слагаемых:
1. линейного относительно x
2. нелинейного, являющегося бесконечно
малой величиной более высокого порядка,
чем x
47.
Дифференциалом функции называетсяглавная, линейная относительно Δх, часть
приращения функции, равная произведению
производной на приращение независимой
переменной:
dy f ( x) x
48.
Найти приращение и дифференциалфункции
y 2 x 3x
2
при х=10 и Δх=0.1
49.
y f ( x x) f ( x)2( x x) 2 3( x x) 2 x 2 3x
(4 x 2 x 3) x
dy f ( x) x 4 x x 3 x
при х=10 и Δх=0.1
y 3.72
dy 3.7
50.
Найти дифференциал функцииy x
51.
dy dx f ( x) x x x xСледовательно, дифференциал
независимой переменной равен
приращению этой переменной:
x dx
52.
Выберемна
графике
функции
произвольную точку М(x,y).
y=f(x)
Дадим аргументу х приращение Δх. Тогда
функция получит приращение
y f ( x x) f ( x)
Проведем касательную к кривой y=f(x) в точке
М(x,y).
Из геометрического смысла производной следует,
что
f ( x) tg
53.
yy f (x)
y y
K
M
y
y
dy
N
x x x x
54.
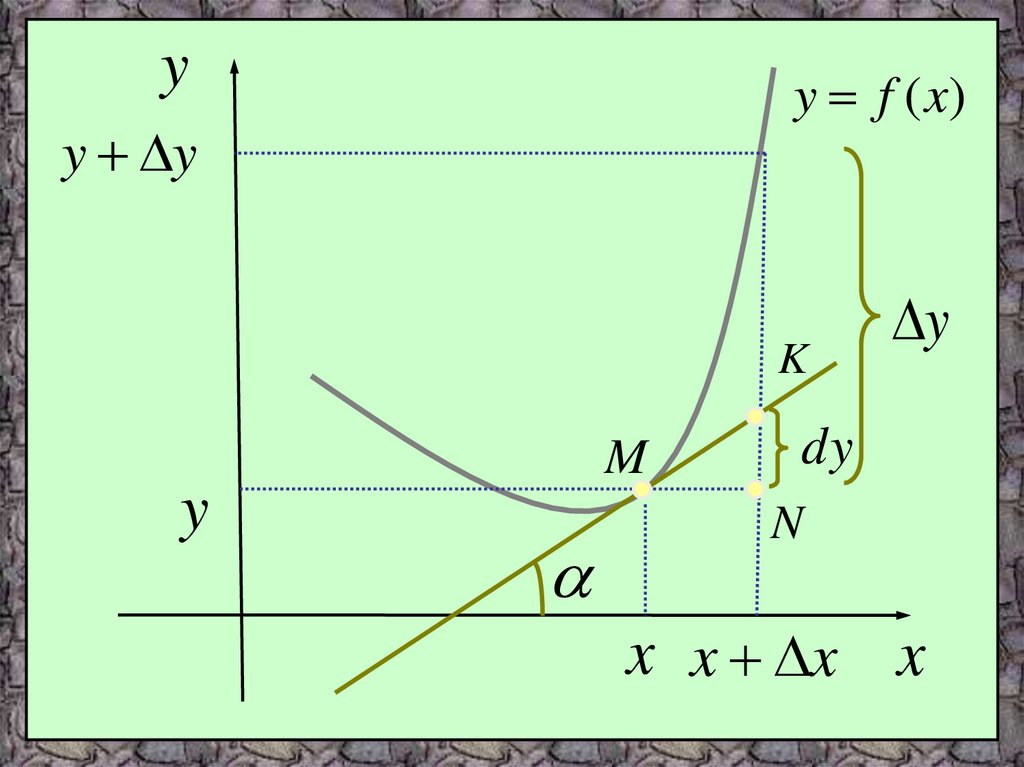
ТреугольникMNK
следовательно
–
прямоугольный,
KN MN tg x f (x)
KN dy
Дифференциал функции есть приращение
ординаты касательной, проведенной к графику
функции y=f(x) в данной точке, когда х получает
приращение Δх.







































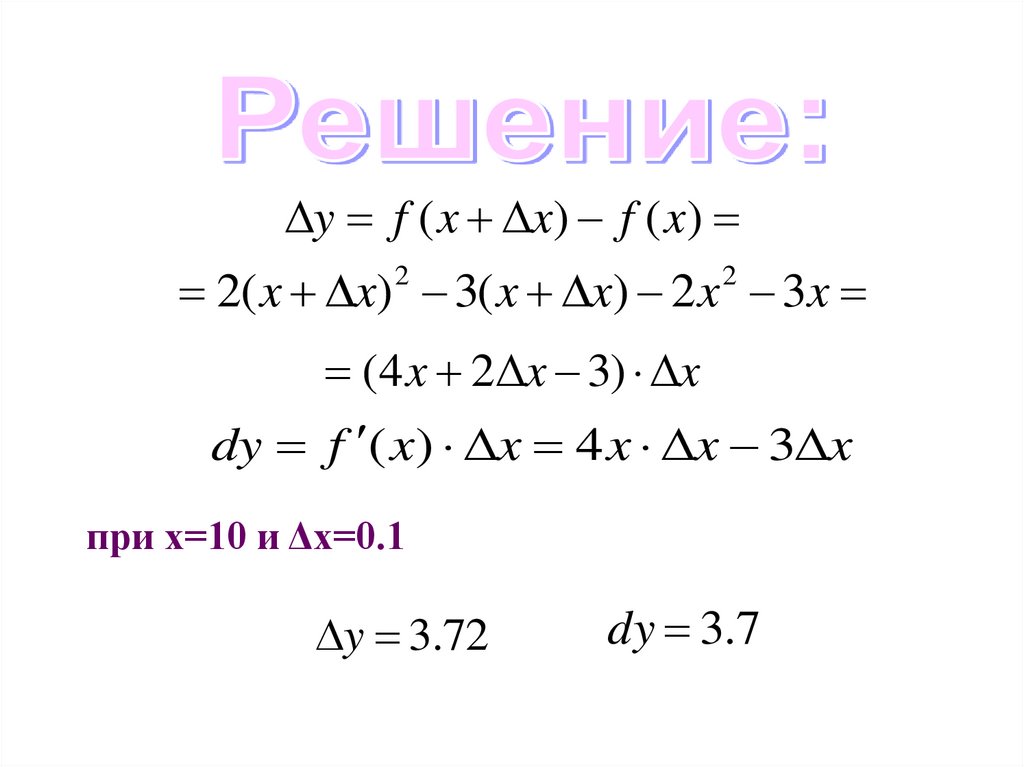




 mathematics
mathematics








