Similar presentations:
Дифференцирование обратной функции
1. Математика. Лекция 11.
Дифференцирование.2. Дифференцирование обратной функции.
Теорема. Пусть функцияy f ( x ) возрастает (или убывает) в некоторой окрестности
x g ( y ). Если в точке x0
и имеет непрерывную обратную функцию
функция y f ( x ) имеет производную y x f ( x0 ) 0, то обратная функция имеет
точки
x0
производную в соответствующей точке y0 f ( x0 ), причем
1
1
x y g ( y 0 )
или x y
.
f ( x0 )
yx
Производная функции y arctgx.
Функция y arctgx, определенная на бесконечной прямой x , является
обратной для функции x tgy, определенной на интервале y . Из формулы
2
2
следует, что
1
1
1
1
y x ( arctgx)
2
2
x y (tgy) 1 sin y cos y
2
2
cos y
cos y
1
1
2
2
.
tg y 1 x 1
1
Итак, ( arctgx)
.
2
1 x
3. Производная функции, заданной параметрически.
Теорема. Пусть зависимость между аргументом х и функцией у заданапараметрическими уравнениями:
x t ,
t ( a , b ),
y
t
,
где t – вспомогательная переменная, называемая параметром. Пусть функции t и
(t ) имеют производные в некоторой точке t ( a , b ) : yt t , xt t 0. Кроме
того, функция x (t ) в окрестности точки t имеет обратную функцию t g ( x ).
Тогда определенная параметрическими уравнениями функция y=f(x) также имеет
производную в точке x t , причем
y'
y' x t .
x' t
4. Производная функции, заданной параметрически.
Пример . Найти производную функции, заданной параметрически:x t 3 5t ,
.
2
y t t 2.
Решение. Имеем: x't 3t 2 5,
Следовательно, производная равна:
y't 2t 1.
y' x
y't
2t 1
2
.
x' t 3t 5
5. Производные высших порядков
Если функция f(x) в каждой точке некоторого промежутка имеет производную, тоэта производная f '(x) является новой функцией на данном промежутке. Если функция
f '(x) тоже имеет производную, то её производная называется второй производной
или производной второго порядка и обозначается y" или f"(x). Таким образом, по
определению:
f ″(x) = (f '(x) )'.
Производная от производной второго порядка, если она существует, называется
третьей производной или производной третьего порядка и обозначается y"' (или f'"(x)):
f ″′(x) = (f ″(x))'.
Производной n-го порядка (или n-й производной) называется производная от
производной (n – 1) порядка:
f(n)(x) = (f(n-1)(x))'.
Начиная с производной четвёртого порядка, производные обозначают римскими
цифрами или числами в скобках (yIV или y(4) – производная четвёртого порядка).
6. Механический смысл второй производной.
Пусть закон движения материальной точки по некоторой прямой линии имеет видS = S(t). Известно , что первая производная S'(t) равна скорости точки в данный момент
времени t:
v(t) = S'(t).
По определению второй производной S"(t) = v'(t), а v'(t) – скорость изменения v(t)
в момент t. Как известно из механики, величина v′(t) является ускорением α в момент
времени t. Итак, вторая производная S"(t) от пути по времени есть ускорение
прямолинейного движения точки:
α(t) = S"(t).
1
Например, если S = gt 2 (g – постоянное ускорение свободного падения), то
2
скорость
v(t) = S'(t) = gt, а ускорение α (t) = v'(t) = S"(t) = g.
7. Правило Лопиталя.
Теорема.Пусть для функций f(x) и φ(х) выполнены следующие условия:
а) они определены и дифференцируемы в некоторой окрестности точки х0 за
исключением, быть может, самой точки х0 , причем φ(х) ≠ 0 и φ'(х) ≠ 0 в указанной
окрестности;
б) функции f(x) и φ(х) при х→х0 совместно стремятся к 0 или ∞ :
lim f ( x) lim ( x) 0
x x0
или
x x0
f ( x ) lim ( x ) ;
lim
x x
x x
0
0
в) существует (конечный или бесконечный) предел отношения производных:
f ( x )
.
lim
(
x
)
x x0
Тогда существует и предел отношения функций, равный пределу отношения
производных:
f ( x)
f ( x )
.
lim
lim
x x0 ( x )
x x0 ( x )
1. Правило Лопиталя справедливо и при х→∞ (при соответствующих условиях).
2. Правило Лопиталя можно применять несколько раз.
8. Правило Лопиталя.
Пример . Найтиx sin x
lim
x 0
3
.
x
x sin x 0
( x sin x )
1 cos x 0
lim
lim
3
2
0 lim ( x 3 )
x
3
x
0
x 0
x 0
x 0
Решение.
(1 cos x )
sin x 0
(sin x )
cos x 1
lim
.
lim
lim
lim
2
6
6
(3 x )
0 x 0 (6 x )
x 0
x 0 6 x
x 0
ln x
Пример . Найти lim
.
x
x
Решение.
ln x
(ln x )
1
0.
lim
lim
lim ( x )
x
x
x
x
x
Пример . Найти
lim
x
x2
.
ex
Решение.
lim
x
( x 2 )
2x
=
lim
lim =
e x x (e x ) x e x
(2 x )
2
= lim x lim x 0.
x ( e )
x e
x2
9. Дифференциал функции.
Определение.Функция y = f(x), имеющая конечную производную в точке
дифференцируемой в точке x.
Пусть функция
y = f(x) имеет в точке x производную
f '(x) = lim
x 0
x, называется
y
. Тогда по
x
теореме о связи предела и бесконечно малой, имеем:
y
f '(x) + α, где lim α = 0.
x 0
x
Умножив обе части последнего равенства на Δx, получим приращение функции Δy в виде:
Δy = f '(x)∙Δx + α∙Δx.
Определение. Дифференциалом функции y = f(x) в точке x называется главная
часть её приращения, равная произведению производной функции на приращение
аргумента. Дифференциал обозначается
dy = f '(x) ∙Δx.
10. Дифференциал функции.
Найдём дифференциал независимой переменной x, т.е. дифференциал функции y = x:dy = dx = (x)'∙Δx = Δx.
Таким образом, dx = Δx.
Поэтому дифференциал функции равен произведению производной функции на
дифференциал независимой переменной:
dy = f '(x)dx.
dy
f ' ( x ).
Из формулы следует равенство
dx
dy
можно рассматривать как отношение
Теперь обозначение производной
dx
дифференциалов dy и dx.
Пример 1. Найти дифференциал функции y = tg3x.
Решение. По формуле находим:
3dx
1
.
=
∙3dx
dy = (tg3x)'dx =
2
2
cos 3x
cos 3x
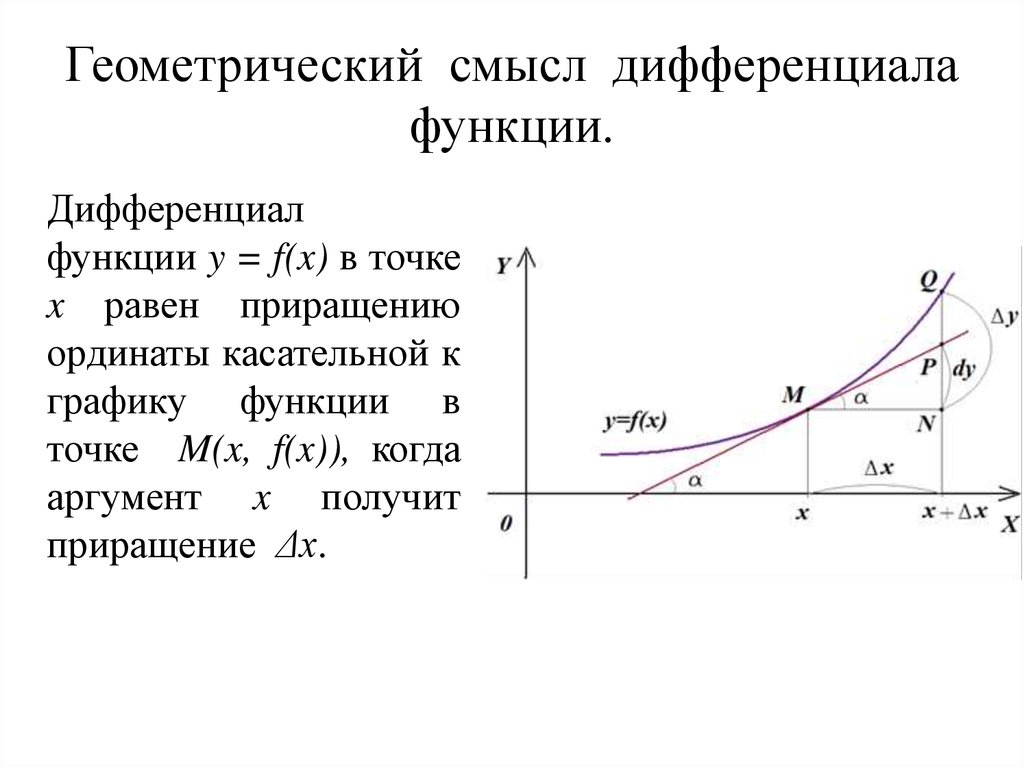
11. Геометрический смысл дифференциала функции.
Дифференциалфункции y = f(x) в точке
x равен приращению
ординаты касательной к
графику функции в
точке M(x, f(x)), когда
аргумент x получит
приращение Δx.
12. Основные свойства дифференциалов.
Свойство 1. Дифференциал постоянной равен нулю:dc = 0.
Действительно:
dc = c'dx = 0∙dx = 0.
Свойство 2. Постоянное число можно выносить за знак дифференциала:
d(cu) = cdu.
Действительно:
d(cu) = (cu)'dx = c∙u'dx = cdu.
Свойство 3. Дифференциал суммы дифференцируемых функций равен сумме
дифференциалов:
d(u + v) = du + dv.
Действительно,
d(u + v) = (u + v)'dx = u'dx + v'dx = du + dv.
13. Основные свойства дифференциалов.
Свойство 4. Дифференциал произведения дифференцируемых функций находитсяпо формуле:
d(uv) = udv + vdu.
Свойство 5. Дифференциал частного дифференцируемых функций находится по
формуле:
u vdu udv
d
( v 0).
2
v
v
Свойство 6. Инвариантность формы дифференциала.
Рассмотрим дифференцируемые функции
u = u(x),
y = f(u). Тогда
дифференциал сложной функции y = f(u(x)) находится по формуле:
dy = f '(u)du.
Если сравним последнюю формулу с определением дифференциала, то
получим, что дифференциал имеет неизменную (инвариантную) форму относительно
аргумента.
Действительно, по формуле производной сложной функции имеем:
dy = (f(u(x)))'dx = f '(u) ∙u'(x)dx = f '(u)du,
т.к. du = u'(x)dx.
14.
Таблица дифференциалов основных элементарных функций.1. d x a ax a 1dx .
2. d ( a x ) a x ln a dx, d (e x ) e x dx.
1
dx
dx, d (ln x ) .
x ln a
x
4. d (sin x ) cos xdx.
5. d (cos x ) sin xdx.
dx
6. d (tgx)
.
2
cos x
dx
7. d (ctgx) 2 .
sin x
dx
8. d (arcsin x )
при x 1.
2
1 x
dx
9. d (arccos x )
при x 1.
2
1 x
dx
10. d (arctgx)
.
2
1 x
dx
11. d (arcctgx )
.
2
1 x
3. d (log a x )
15. Применение дифференциала в приближенных вычислениях значений функции.
Перейдем к применению дифференциала в приближенных вычисленияхзначений функции.
Пусть известно значение функции
и её производной в точке .
Покажем, как найти значение функции в точке х, близкой к
.
.
Рассмотрим приращение функции
при малых приращениях аргумента
:
y dy y ' dx y ' x
Так как
откуда
, то
,
.
Пример. Вычислим приближенно 1,0003 с помощью дифференциала.
Для этого используем функцию y x . Найдем значение этой функции
при x 1,0003 . Ближайшее к нему значение, для которого точно известно
значение функции – это x0 1 , значение функции y0 1 1 .
Найдем производную функции, чтобы применить приближенную формулу.
y '
1
2 x
, значение производной y ' (1)
1
2
В результате 1,0003 1 (1,0003 - 1) 1
0,0003
1,00015 .
2
1
2 1
1
.
2














 mathematics
mathematics








