Элементы дифференциального исчисления

1. Элементы дифференциального исчисления

2. Дифференциальное исчисление функций одной переменной

1. Производные
2. Таблица производных
3. Дифференциал
4. Производные и дифференциалы
высших порядков
5. Некоторые теоремы о
дифференцируемых функциях
6.Применение производных к
исследованию функций
7. Общая схема исследования функции и
построение графика

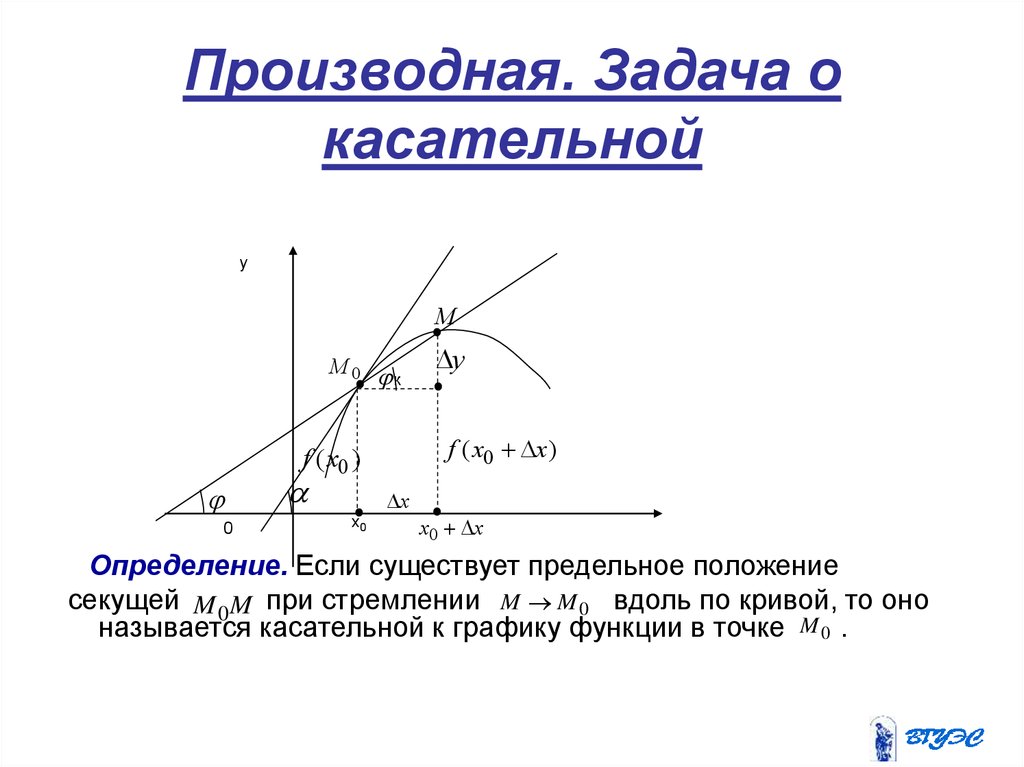
3. Производная. Задача о касательной

y
М
М0
к
f ( x0 x)
f ( x0 )
0
y
x
x0
x0 x
Определение. Если существует предельное положение
секущей M 0 M при стремлении M M 0 вдоль по кривой, то оно
называется касательной к графику функции в точке M 0 .

4. Производная. Задача о касательной

Обозначим угол наклона касательной к
графику функции в точке M 0 .
y
x
0
,
Очевидно,
при
а tg
x
стремится к tg
y
tg lim tg lim
.
x 0
x 0 x
Тогда угловой коэффициент
y
касательной равен k lim
.
k tg
x 0
x

5. Производная. Определение

Пусть функция у = f x определена в
интервале a, b и пусть точка x0 a, b .
Рассмотрим далее точку x0 x a, b .
В обеих точках вычислим значения
функции и разность y f ( x0 x) f ( x0 ) .
Эту разность будем называть
приращением функции в
фиксированной точке x0 .

6. Производная. Определение

Если существует конечный (или
бесконечный)
y
f x0 x f x0
= lim
,
lim
x
x
0
x
x 0
то он называется конечной (или
бесконечной) производной функции f x
в точке x0 и обозначается
'
символами у ' или f x0 ,
т.е.
y
y lim
.
x 0 x
'

7. Примеры

Ясно, что угловой коэффициент
касательной равен производной в точке
касания. Приведем примеры.
y
y
f ' ( x0 ) 0
y'
в точке
0
x0
x 0

8. Уравнение касательной

Касательную как прямую, проходящую
через точку касания M 0 ( x 0 ; y 0 ) , задают
уравнением y y 0 y 0 ( x x 0 ).
Например, уравнение касательной к
2
кривой y x в точке (1;2) имеет вид
у-2=2(х-1) или 2х-у=0.

9. Теоремы о производных

Теорема 1. Если существуют
'
производные u x и
v' x функций u (x) и v x , то
существуют
u x v x ' u v ' u' v' ;
u v ' u' v uv' ;
u u ' v uv'
v 0 .
2
v
v

10. Теоремы о производных

Следствие.
cy ' c' y cy' cy' , так как c' 0 ,
т.е. постоянный множитель
выносится за знак производной.

11. Теоремы о производных

Теорема 2. Если функция в
точке x0 имеет производную, то она
в этой точке непрерывна.
Обратное неверно. Возможен
случай, когда непрерывная функция
не имеет производной в точке
непрерывности.

12. Теоремы о производных

Например:
y
y x
y' не существует в точке
x 0
x

13. Примеры

Выведем формулы некоторых
производных, применяя определение
производной:
1) y x 2 имеет производную
y' lim
x x 2 x 2
x 0
x
x 2 2 x x x 2 x 2
2 x x x 2
lim
lim
x
x
x 0
x 0
lim 2 x x 2 x ;
x 0

14. Примеры

x x
x
x x
e
e
e
e 1
x
2) e ' lim
lim
x
x
x 0
x 0
x
e
1
x
e lim
e x 1 e x .
x 0 x
Таким же образом можно получить
производные sin x ' cos x , cos x ' sin x , а
по правилу вычисления производных
сложных функций можно вычислить и
другие производные.

15. Производная обратной функции

Теорема. Пусть функция х=f(y)
монотонна и дифференцируема в
некотором интервале (a,b) и имеет в
точке у этого интервала не равную нулю
f ( y ) в
производную
. Тогда
соответствующей точке х обратная
1
y
f
( x) имеет производную
функция
1
1
1
[ f ( x)]
или y x
.
f ( y )
x y

16. Примеры

Для функции y=arcsinx обратной
является функция x=siny , которая в
интервале (-π/2;π/2) монотонна и
дифференцируема. Ее производная в
этом интервале в нуль не обращается.
Поэтому
1
1
1
1
y x
.
x y cos y
1 sin 2 y
1 x2

17. Примеры

Итак, (arcsin x)
1
1 x2
.
Аналогично можно получить
(arccos x)
1
1 x2
1
(arctgx)
,
2
1 x
1
(arcctgx)
.
2
1 x
,

18. Теорема о производной сложной функции

Пусть функция u u x имеет
производную в точке x0 , а функция
y f u имеет производную в точке
u0 u x0 . Тогда сложная функция
y f u x имеет производную в точке x0 ,
причем y' f ' u 0 u' x0 .
Или: y' f 'u u ' x в произвольной точке
x.

19. Производная степенной функции

Справедливо тождество
Тогда
x e
n
y (e ) e (n ln x)
n n ln x n n n 1 n
n 1
e x nx , ( x ) nx .
x
x
n ln x
n ln x
n ln x
.

20. Производные гиперболических функций

Гиперболическими называют функции
x
e e
e e
shx
; chx
2
2
shx
chx
thx
; cthx
.
chx
shx
x
x
x
;

21. Производные гиперболических функций

Поэтому
1 x
1 x
x
x
( shx ) (e e ) (e e ) chx.
2
2
(chx) shx;
shx
ch 2 x sh 2 x
1
(thx) (
)
2 ;
2
chx
ch x
ch x
1
(cthx) 2
sh x.

22. Таблица производных

7. log a u '
1. c ' 0,
2. (u )' nu
n
3.
u ' 2
n 1
1
u' ,
u' ,
u
1
1
4. ' 2 u ' ,
u
u
5. a ' a ln a u ' ,
u
u
6. e u ' e u u ' ,
1
u' ,
u ln a
1
8. ln u ' u ' ,
u
9. sin u ' cos u u ' ,
10. cos u ' sin u u ' ,
1
11. tgu '
u' ,
2
cos u
1
12. ctgu '
u' ,
2
sin u

23. Таблица производных

13. (arcsin u )
(arccos u )
1
1 u2
14. ( shu) chu u .
.u
1
1 u2
u ,
1
(arctgu )
u ,
2
1 u
1
(arcctgu )
u .
2
1 u
(chu) shu u ;
1
u ;
2
ch u
1
(cthu) 2 u
sh u.
(thu)

24. Дифференцируемая функция

Определение. Если функция f x в
точке x имеет (конечную) производную, то
она называется дифференцируемой в этой
точке.
Если функция дифференцируема в
каждой точке некоторого промежутка, то
она называется дифференцируемой на
этом промежутке.

25. Дифференциал функции

Рассмотрим пример. Найдем
приращение функции y x 2 в точке x0 .
Известно, что y f x0 x f x0 .
В нашем примере
f x0 x0 2 , f x0 x x0 x 2 , а
приращение.
y x0 x 2 x0 2 x0 2 2 x0 x x 2 x0 2
Итак, y 2x0 x x 2 , где, как известно, 2x0
является производной функции x 2 в точке
x0 .

26. Определение дифференциала

Пусть приращение функции в точке
может быть представлено в виде
y A x o( x) , где x приращение аргумента, А-величина, не
зависящая от x , o( x) -бесконечно
малая более высокого порядка ,
чем x при x 0.

27. Определение дифференциала

Тогда главная линейная относительно
x часть приращения функции
называется дифференциалом функции
в точке и обозначается dy .
Итак, по определению dy A x .
Теорема. Для того чтобы в точке х
функция имела дифференциал,
необходимо и достаточно, чтобы она в
этой точке имела производную.

28. Дифференциал функции

Приращение аргумента x в этом
случае принято обозначать dx и тогда
dy f ' x0 dx , где dx x . В
произвольной точке x dy f ' x dx .
Замечание. Из последней формулы
получается еще одно обозначение
dy
производной f ' x
.
dx

29. Дифференциал функции

Пример.
d sin x cos xdx;
1
1
d tgx
dx; d ln x dx;
2
x
cos x
2
d x 2 xdx;
d x a dx

30. Дифференциал функции

Как и для производной, для
дифференциала функции имеют
место формулы:
1. d u v du dv;
2. d uv vdu udv ;
u vdu udv
v 0 ;
3. d
2
v
v
4. d (cu) cdu .

31. Инвариантность дифференциала

По правилу дифференцирования
сложной функции
dy yu u x dx yu (u x dx) y du.
Здесь форма дифференциала остается
неизменной, но под дифференциалом
аргумента понимается не приращение
этого аргумента, а его дифференциал.

32. Производные высших порядков

Введем теперь понятие производной
второго порядка функции f x .
Производную от первой производной
функции f x , т.е. y ' ' будем называть
производной второго порядка (тогда y ' производная первого порядка) и будем ее
обозначать y ' ' или f ' ' x . Далее
y' ' y' ' ' f ' ' ' x - это производная
третьего порядка, … а y n 1 ' y n - это
производная n-го порядка.

33. Дифференциалы высшего порядка

Дифференциал от дифференциала
данной функции называется ее
дифференциалом второго порядка и
2
2
обозначается d y d f ( x) . По
определению
d y d (dy) d ( f ( x)dx) ( f ( x)dx) dx f ( x)dx .
2
2
2
d y f ( x)dx ,
2
Итак,
d y f ( x)dx
3
3
и т.д.

34. Дифференцирование функций, заданных параметрически

Пусть функция у от х задана
параметрическими уравнениями
x x(t ), y y (t ), t ( , ).
И пусть эти функции
dy yt dt yt
дифференцируемы. Тогда
dx xt dt xt
Если существует вторая производная,
то
( y x ) t
y xx
xt

35. Пример

Найти производную функции
Имеем
x a(t sin t ),
y a(1 cos t ).
t
t
2 sin cos
a sin t
t
2
2
y x
ctg .
a(1 cos t )
2
2 t
2 sin
2
y xx
1
t
2a sin
(1 cos t )
2
2
1
t
4a sin
2
4
.

36. Производные неявных функций

Пусть значения х и у связаны
уравнением F(x,y)=0. Если функция
у=f(х), определенная на некотором
промежутке, при подстановке ее вместо
у в уравнение F(x,y)=0 обращает это
уравнение в тождество, то говорят, что
это уравнение задает функцию у=f(х)
неявно.

37. Пример

Продифференцируем функцию
y x ln y .
1
Имеем y 1 y. Отсюда
y
1
y (1 ) 1,
y
y
y
.
y 1

38. Продолжение

Найдем вторую производную.
y
Так как y
, то
y 1
y
y ( y 1) yy
y ( y 1 y )
( y 1)
( y 1)
y
y
.
2
3
( y 1)
( y 1)
2
2

39. Логарифмическое дифференцирование

Найти производную функции y (cos x) .
Прологарифмируем обе части:
ln y x cos x. Теперь берем
производную
y
cos x x sin x, y y (cos x x sin x).
y
x
Окончательно
y (cos x) x (cos x x sin x).