Дифференциальное исчисление функций одного аргумента

1. ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ ФУНКЦИЙ ОДНОГО АРГУМЕНТА

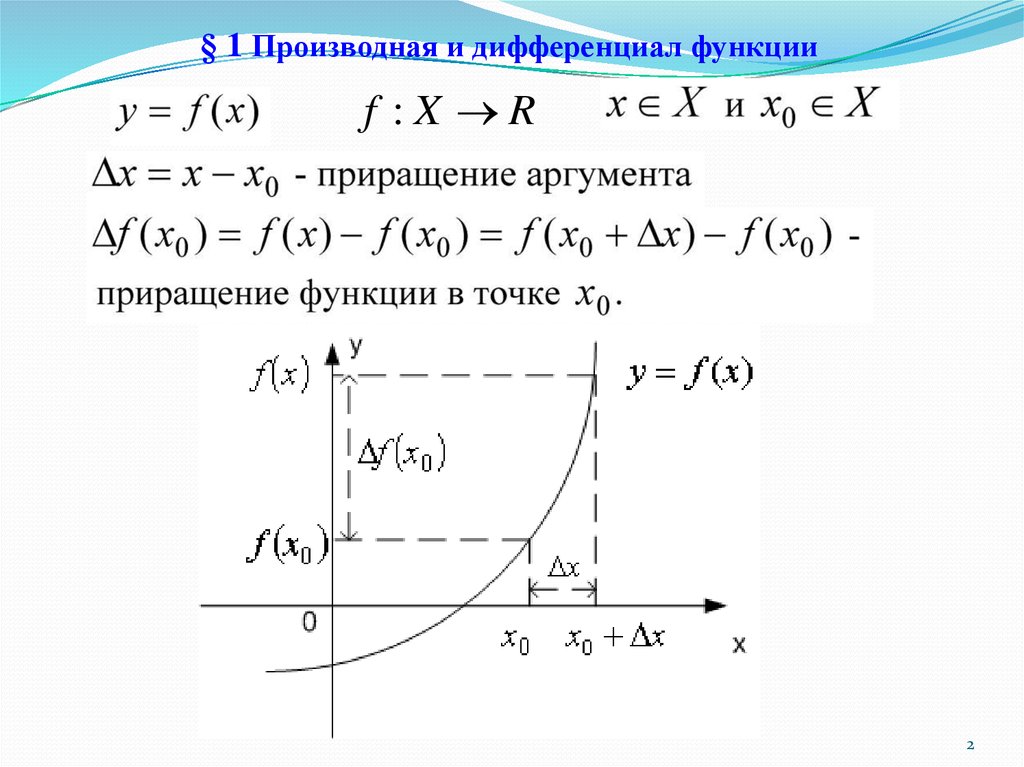
1

2. § 1 Производная и дифференциал функции

f :X R
2

3.

3

4.

4

5.

f ( x),
y ,
df
,
dx
y x
5

6.

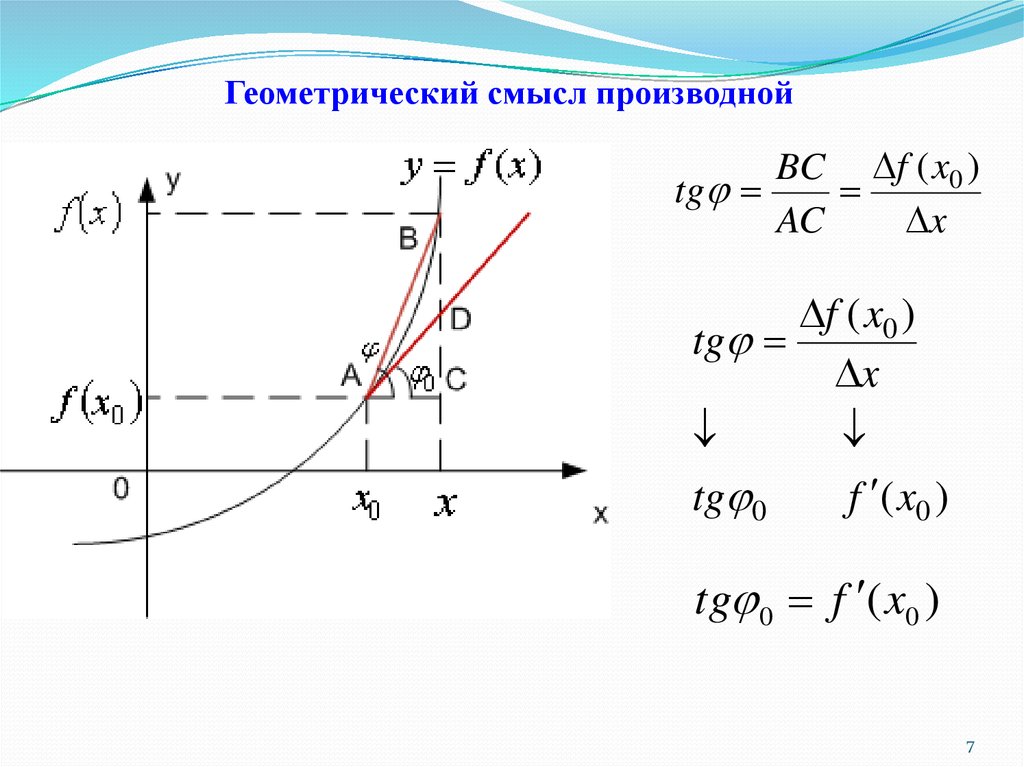
6

7. Геометрический смысл производной

BC f ( x0 )
tg
AC
x
f ( x0 )
tg
x
tg 0
f ( x0 )
tg 0 f ( x0 )
7

8.

y f ( x0 ) f ( x0 )( x x0 )
1
y f ( x0 )
( x x0 )
f ( x0 )
8

9. Механический смысл производной

S (t ) S (t0 )
vср
t t0
t t0 0
t t0
S (t ) S (t0 )
S (t0 )
v мгн lim
t t0
t t0
S (t ) v
9

10. §2 Основные правила дифференцирования

10

11.

11

12.

12

13. §3 Производные основных элементарных функций

13

14.

f ( x)
g ( x)
f ( x) g ( x ) g ( x) ln( f ( x)) g ( x) f ( x)
f
(
x
)
14

15. §4 Дифференциал функции одного аргумента

1. dc 0
2. d (cf ) cdf
dy f ( x)dx
3. d ( f g ) df dg
4. d ( fg ) fdg gdf
f gdf fdg
5. d
g2
g
Инвариантность формы дифференциала.
y f (u)
u u(x)
dy d f u ( x) f u ( x) dx f (u )u ( x)dx f (u )du
dy f (u )du
15

16.

Применение дифференциала в приближенных вычислениях
y dy ( x) x
dy f ( x) x
y dy
f ( x x) f ( x) f ( x) x
f ( x x) f ( x) f ( x) x
16

17. §5 Производные и дифференциалы высших порядков

f
( n)
( x) f
( n 1)
( x)
Физический смысл производной второго порядка:
S (t ) S (t ) v (t ) a(t )
d y d (d
n
d y f
n
( n)
n 1
y)
( x)dx
n
17

18.

18

19.

19

20.

20

21.

§ 7 Правила Лопиталя
0
0
f ( x)
f ( x)
lim
lim
x x0 g ( x)
x x0 g ( x)
21

22.

§ 8 Формула Тейлора
pn ( x) a0 a1 ( x x0 ) a2 ( x x0 ) 2 ... an ( x x0 ) n ,
x0 R, n N , ai R
ak
(k )
pn ( x0 )
k!
pn( k ) ( x0 )
k
pn ( x )
( x x0 )
k!
k 0
n
22

23.

n
(k )
f n ( x0 )
k 0
k!
f ( x)
( x x0 ) Rn ( x)
k
формула Тейлора
n
(k )
f n ( x0 )
k 0
k!
pn ( x )
( x x0 )
k
f ( x) pn ( x) Rn ( x)
n
(k )
f n ( x0 )
k 0
k!
f ( x)
( x x0 )
k
23

24.

n
(k )
f n ( x0 )
k 0
k!
f ( x)
( x x0 )
k
f
( n 1)
(c )
n 1 !
x x0
n 1
24

25.

f ( k ) (0) k
f ( x)
x Rn ( x)
k!
k 0
n
n
f ( x)
k 0
f
(k )
Формула Маклорена
( n 1)
(c) n 1
( 0) k f
x
x
n 1 !
k!
25

26.

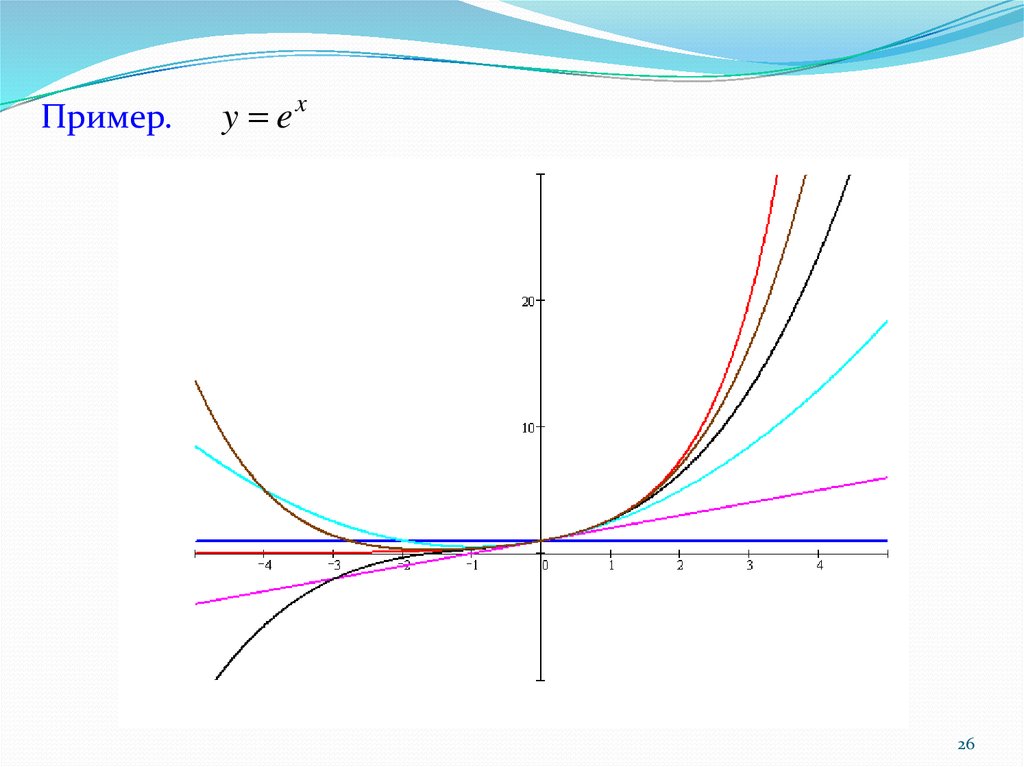
Пример.
y ex
26

27.

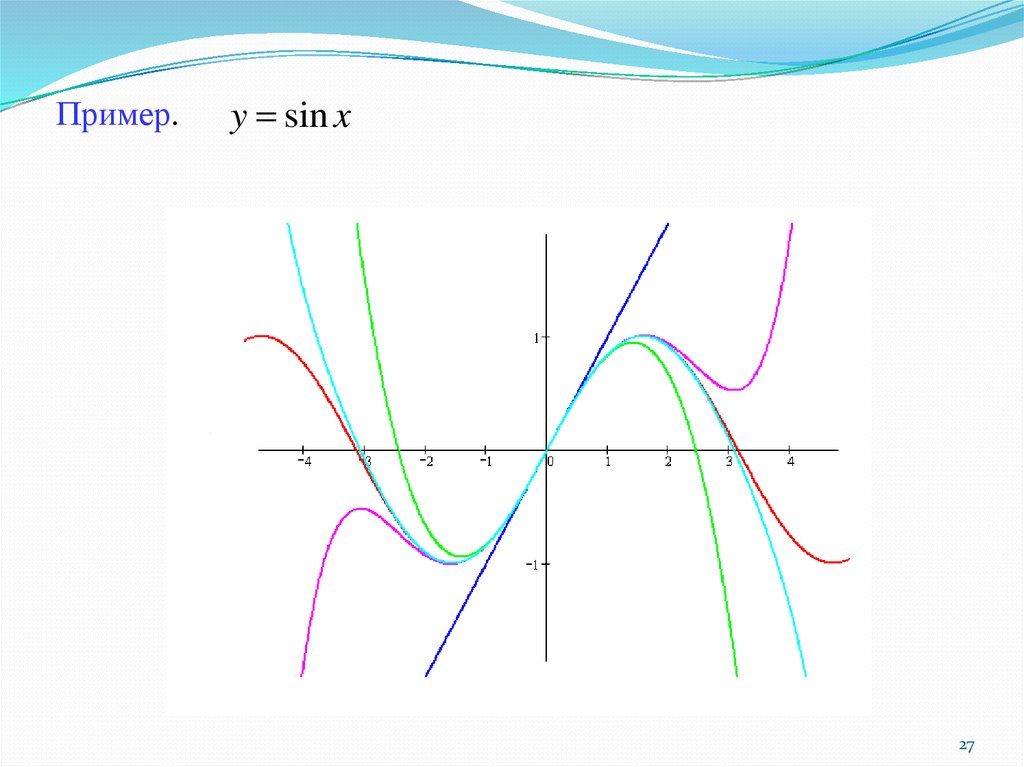
Пример.
y sin x
27

28. § 10 Экстремум функции

28

29.

29

30.

30

31.

31