Similar presentations:
Дифференциальное исчисление
1. Раздел V. Дифференциальное исчисление
• Определение производной• Геометрический и механический смысл
производной
• Дифференциал функции. Основные
правила дифференцирования
• Таблица производных элементарных
функций
Насырова Р.Т.
2. Определение производной
Пусть функция y = f(x) определена в некотором интервале (a; b).Аргументу x придадим некоторое приращение
x0 x (a; b)
x :
Найдем соответствующее приращение функции:
y f ( x0 x) f ( x0 )
y
Если существует предел
f(x0+ Δx )
f(x 0 )
y
x
0
х 0 x 0 +Δx х
y
lim
x 0
x
то его называют производной
функции y = f(x) и обозначают
одним из символов:
y ;
f ( x );
dy
dx
3. Определение производной
Итак, по определению:f ( x x ) f ( x )
y lim
x 0
x
Производной функции в
точке x0 называется предел
отношения приращения
функции ∆y к вызвавшему его
приращению аргумента ∆x в
этой точке при ∆x→0.
Функция y = f(x) , имеющая производную в каждой точке интервала
(a; b), называется дифференцируемой в этом интервале;
операция нахождения производной функции называется
дифференцированием.
Значение производно функции y = f(x) в точке x0 обозначается
одним из символов:
y ( x0 );
f ( x0 );
y x
0
Если функция y = f(x) описывает какой – либо физический процесс,
то f ’(x) есть скорость протекания этого процесса – физический
смысл производной.
4. Геометрический смысл производной
Возьмем на непрерывной кривой две точки М и М1:y
М1
f(x0+ Δx )
f(x0 )
α φ
0
y
М
x
х0 x0+Δx х
Через точки М и М1 проведем
секущую и обозначим через φ
угол наклона секущей.
y
tg
x
f ( x0 x ) f ( x0 )
x
При x 0 в силу непрерывности функции y также
стремится к нулю, поэтому точка М1 неограниченно приближается
по кривой к точке М, а секущая ММ1 переходит в касательную.
lim lim tg tg
x 0
x 0
5. Геометрический смысл производной
f ( x0 x) f ( x0 )lim
tg k y
x 0
x
Производная f ’(x) равна угловому коэффициенту касательной к
y которой равна x.
графику функции y = f(x) в точке, абсцисса
Если точка касания М имеет координаты (x0; y0 ), угловой
коэффициент касательной есть k = f ’(x0 ).
Уравнение прямой с угловым коэффициентом:
y y 0 кf '((xx-0 )(
x 0x)- x 0 )
Уравнение
Уравнение
касательной
нормали
Прямая, перпендикулярная касательной в точке касания,
называется нормалью к кривой. f ' ( x 0 )
k норм
1
1
1
y y0
( x x0 )
k кас
f ' ( x0 )
f ' ( x0 )
6.
Механический смысл производнойРассмотрим простейший случай: движение материальной точки вдоль
координатной оси. При этом задан закон движения точки:
координата x движущейся точки – это известная функция времени x(t).
В течение интервала времени от t0 до t0+∆t точка
перемещается на расстояние
Средняя скорость точки
находится по формуле:
При ∆t→0 значение средней скорости стремится к определённой
величине, которая в физике называется мгновенной
скоростью
материальной точки в момент времени .
Следовательно, для мгновенной скорости можно записать
формулу
Если сравнить эту формулу с формулой производной, то можно
сделать вывод, что cкорость – это производная координаты по
времени
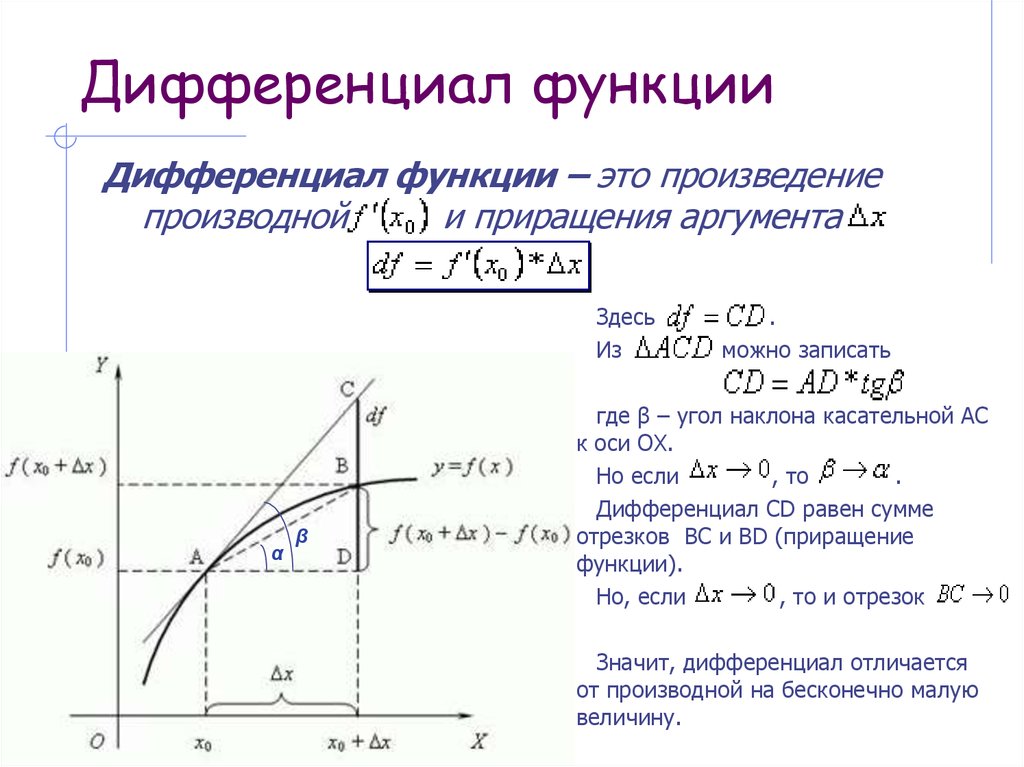
7. Дифференциал функции
Дифференциал функции – это произведениепроизводной
и приращения аргумента
Здесь
Из
α
β
.
можно записать
где β – угол наклона касательной АС
к оси ОХ.
Но если
, то
.
Дифференциал CD равен сумме
отрезков BС и BD (приращение
функции).
Но, если
, то и отрезок
Значит, дифференциал отличается
от производной на бесконечно малую
величину.
8. Таблица производных простейших элементарных функций
9. Правила дифференцирования
Пусть u(x) , v(x) и w(x) – дифференцируемые в некотороминтервале (a; b) функции, С – постоянная.
(C ) 0
(u v ) u v
(u v ) u v u v (C u ) C u
(u v w ) u v w u v w u v w
u u v u v
C
C
v
2
2
v
v
v
v
10. Правила дифференцирования
11. Производная сложной функции
Пусть y = f(u) и u = φ(x) , тогда y = f(φ(x)) – сложная функция спромежуточным аргументом u и независимым аргументом x.
Теорема
Если функция u = φ(x) имеет производную u x в точке x а
функция y = f(u) имеет производную y u в соответствующей точке
u , то сложная функция имеет производную y x , которая
находится по формуле:
y x y u u x
Это правило остается в силе, если промежуточных аргументов
несколько:
y f (u );
u (v );
v g( x )
y x y u uv v x
y f ( (g ( x )))
12. Пример
Вычислить производную функцииy cos(ln12 x )
Данную функцию можно представить следующим образом:
y cos u; u v 12 ; v ln x
y x y u uv v x
y u sin u sinv 12 sin ln12 x
u 12v 11 12 ln11 x
1
v
x
y sin ln12 x 12 ln11 x
Коротко:
y (cos(ln 12 x )) sin(ln 12 x ) (ln12 x )
sin(ln 12 x ) 12 ln11 x (ln x )
1
x
13.
Формирование подгрупппроисходит по методу
жеребьёвки
Подгруппа 1
Группа БТПп-15-21
Подгруппа 2
Даётся 2 минуты на
распределение
обязанностей внутри
подгруппы
Подгруппа 3
Подгруппа 4
Координатор (1)
• Распределяет задания, данные в пакете, внутри своей подгруппы между всеми участниками
• Отвечает сам на контрольные вопросы
Аналитик (1)
• Анализирует работу каждого участника своей подгруппы
• Выставляет каждому очки (от 0 до 10) в соответствии с критериями оценивания
Критик (1)
• Анализирует работу каждого участника соседней подгруппы (1 у 2, 2 у 3, 3 у 4, 4 у 1)
• Выставляет каждому очки (от 0 до 10) в соответствии с критериями оценивания
Исполнитель (5)
• Изучает содержимое теоретической части пакета
• Выполняют данную координатором работу для последующего ее представления проверяющим с
учётом требований












 mathematics
mathematics








