Similar presentations:
Интегрирование некоторых видов иррациональностей
1.
В ряде случаев замена переменной позволяетсвести интегралы от иррациональных
функций к интегралам от рациональных.
Пусть R(u,v) – функция от переменных u,v и
некоторых
постоянных,
которая
построена с использованием всего четырех
действий:
сложения,
вычитания,
умножения и деления, например:
5
R(u, v) u
v
2
2.
1Интегралы вида:
R x,
n
x dx
Замена переменной:
t x
n
3.
Вычислить интеграл:1
dx
3
x x
4.
1dx
3
x x
t 6 x
x t6
dx 6t 5 dt
6t 5
3
dt
2
t t
t 1 u
t3
(u 1)3
6
dt
6
du
dt du
t 1
u
u 3 3u 2 3u 1
6
du
u
5.
16 u du 18 udu 18 du 6 du
u
2
2u 9u 18u 6 ln u C
3
2
2(t 1) 9(t 1) 18(t 1)
3
2
6 ln t 1 C
2( x 1) 9( x 1) 18( x 1)
6
3
6
2
6 ln 6 x 1 C
6
6.
2Интегралы вида:
ax b
n
R x, cx d
dx
Замена переменной:
ax
b
t n
cx d
7.
Вычислить интеграл:1 x
1
dx
1 x 1 x
8.
1 xt
1 x 1
1 x
dx
4t
1 x 1 x
dx
(1 t 2 ) 2
1 t 2
t
2
1 t 2
x
1 t 2
2
1 x
1 t 2
4t
dt
2 2
(1 t )
t2
(t 2 1) 1
2
dt 2
dt
2
2
1 t
1 t
9.
(t 1)1
2
dt 2
dt
2
2
1 t
1 t
2
2t 2arctgt C
1 x
1 x
2
2arctg
C
1 x
1 x
10.
3Интегралы вида:
Ax B
ax bx c
2
dx
11.
Под корнем выделяется полный квадрат иделается линейная замена переменной, так
что интеграл сводится к виду:
Mx N
ex 2 f
dx M
x
ex 2 f
dx N
1
1
ex 2 f
dx
2
Для нахождения первого интеграла делается
замена:
t ex f
2
Тогда
12.
ex 2 f tx
1
1
dx
dt
2
2e
dt 2exdx
t
ex f
1
1
2
t C
ex f C
e
e
Второй интеграл при
1
а при
x2 a
e f 0
e f 0
будет табличным:
dx ln x x 2 a C
будет табличным:
1
x
dx arcsin C
2
2
a
a x
13.
1Вычислить интеграл:
x
dx
2
x 4x 5
14.
xx2 4x 5
dx
x 2 t
dt dx
t
t 2 1
x
( x 2) 2 1
dt 2
t 2
t 2 1
dt
1
t 2 1
t 2 1 u
du 2tdt
dx
dt
15.
1 12
du 2 ln t t 1
2
u
u 2 ln t t 1 C
2
t 1 2 ln t t 1 C
2
x 2 1 2 ln x 2 ( x 2) 1 C
2
16.
2Вычислить интеграл:
x
dx
2
8 4x 4x
17.
x8 4x 4x2
1 2x t
dt 2dx
dx
x
9 (1 2 x) 2
1 t
2
9 t2
dx
1
dt
2
1
1 t
dt
4
9 t2
1
4
1
1
dt
4
9 t2
t
9 t2
dt
18.
9 t2 u1
t 1 1
du
arcsin
4
3 8
u
du 2tdt
1
t 1
arcsin
u C
4
3 4
1
t 1
arcsin
9 t2 C
4
3 4
1
1 2x 1
arcsin
9 (1 2 x) 2 C
4
3
4














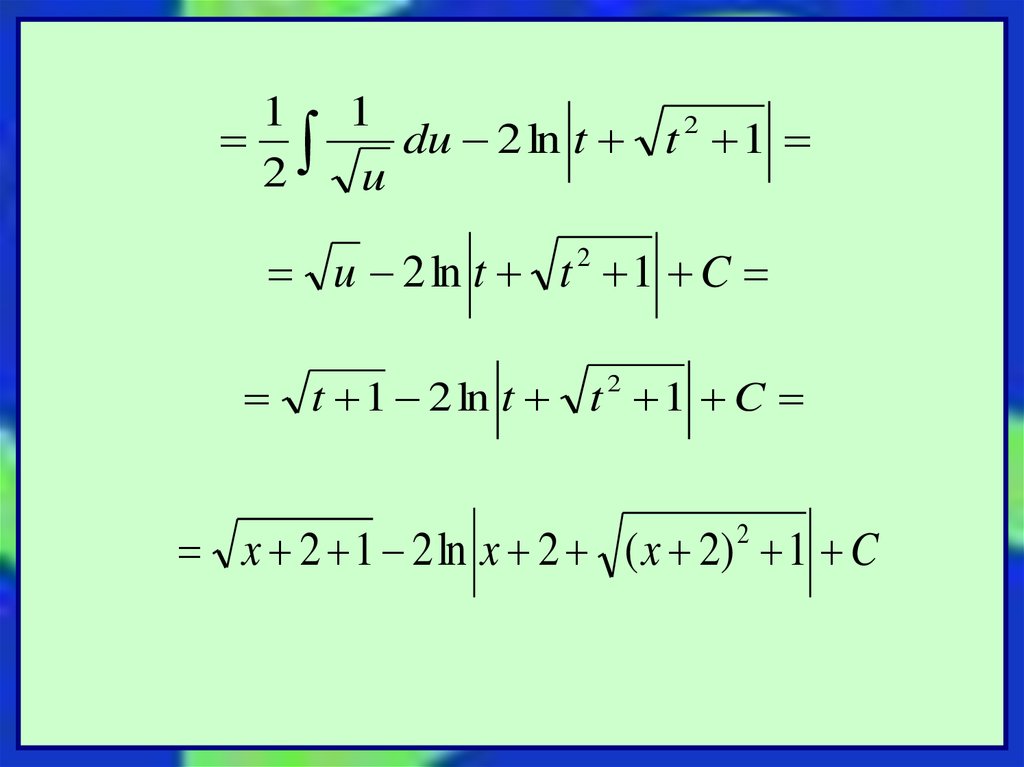



 mathematics
mathematics








