Similar presentations:
Сведение двойного интеграла к повторному
1.
Рассмотримспособ
вычисления
двойных
интегралов путем сведения их к повторному
интегралу.
Сформулируем теорему.
2.
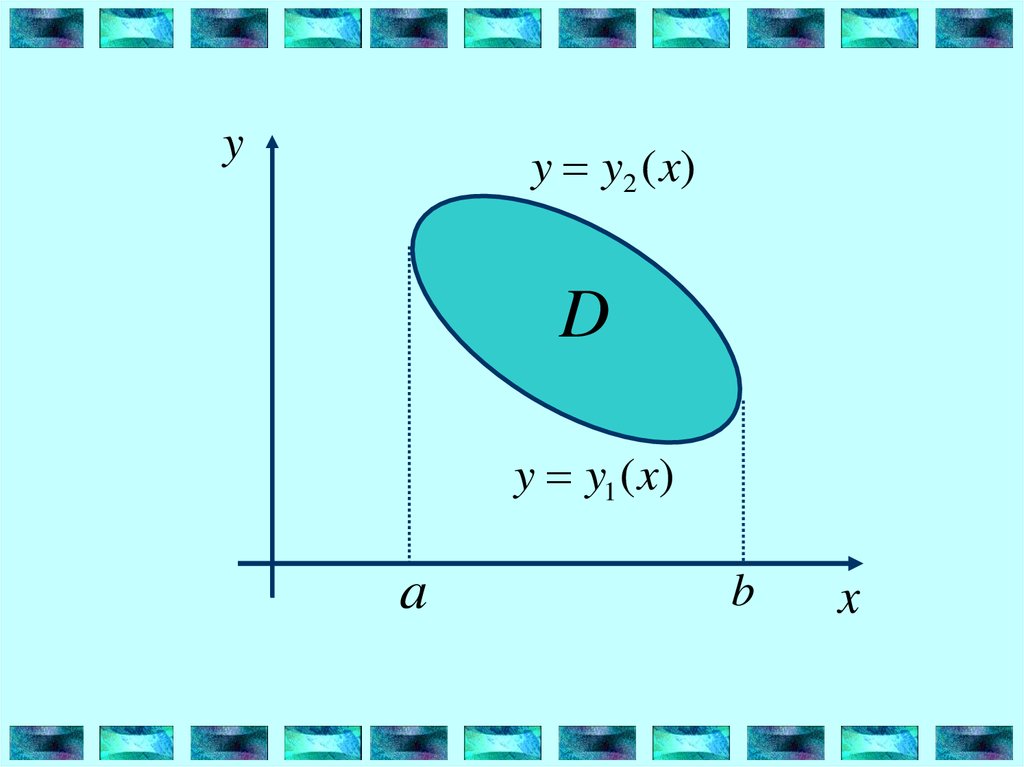
Пусть функция z=f(x,y) определена иинтегрируема в области D, ограниченную
снизу и сверху двумя непрерывными
кривыми y=y1(x) и y=y2(x), причем
y1 ( x ) y y2 ( x )
a x b
Пусть для любого х из отрезка [a,b]
существует определенный интеграл
3.
I ( x)y2 ( x )
f ( x , y )dy
y1 ( x )
Тогда существует повторный интеграл
b
b
y2 ( x )
a
a
y1 ( x )
I ( x )dx dx f ( x , y )dy
и выполняется равенство:
4.
by2 ( x )
a
y1 ( x )
f ( x, y)dxdy dx f ( x, y)dy
D
5.
yy y2 ( x)
D
y y1 ( x)
a
b
x
6.
Если D –прямоугольная область, т.е.y1 ( x) c
y2 ( x) d
тогда
b
d
a
c
f ( x, y)dxdy dx f ( x, y)dy
D
7.
1Вычислить двойной интеграл
3 x
2
y 2 x dxdy
3
D
D 0 x 1, 1 y 2
8.
3xD
2
1
2
y 2 x dxdy dx (3x y 2 x )dy
3
2
0
1
2
1
3
3 2 2
9 2
3
3
dx x y 2 x y x 2 x dx
2
1 0 2
0
1
1
3 1
3 3 1 4
x x 1
2 0 2 2
2
9.
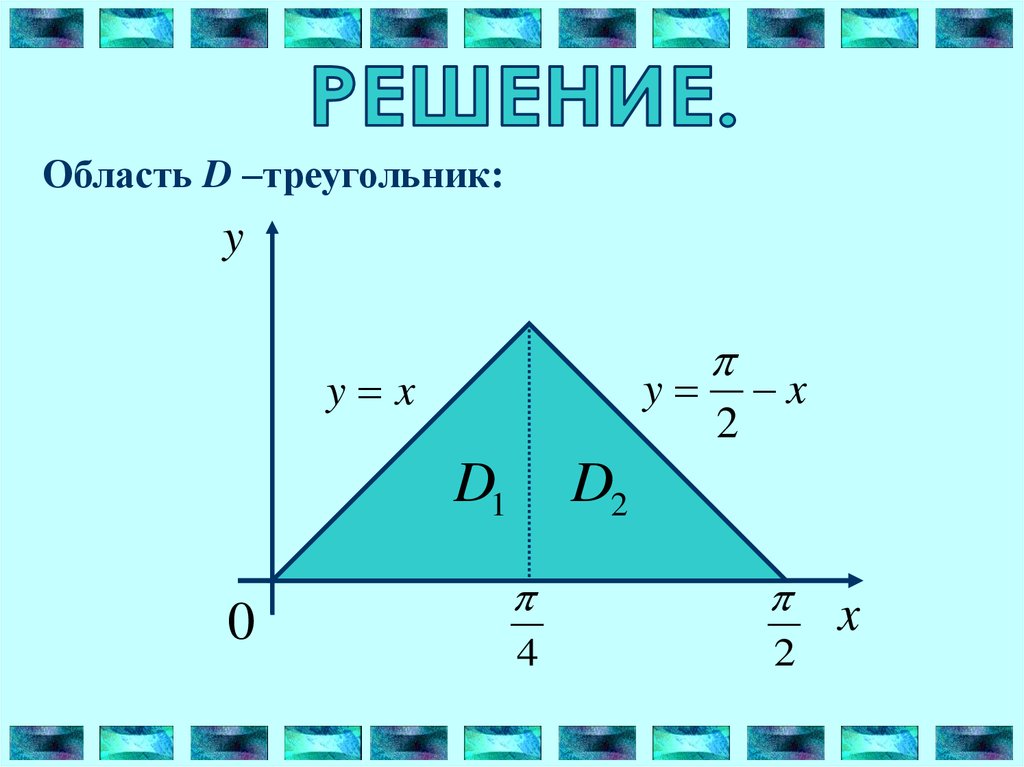
2Вычислить двойной интеграл
sin( x y ) dxdy
D
где область D ограничена линиями
x y,
x y
2
,
y 0
10.
Область D –треугольник:y
y
y x
D1
0
2
x
D2
4
2
x
11.
sin( x y) dxdy sin( x y) dxdy sin( x y) dxdyD
D1
D2
x
4
x
2
2
dx sin( x y) dy dx sin( x y) dy
0
0
4
0
4
2
x
2
dx cos( x y ) 0 dx cos( x y ) 0
0
4
x
4
2
dx (cos 2 x cos x) dx (cos
0
4
2
cos x)
12.
41
sin 2 x sin x sin x 2
4
2
0
1
2
2 1
1
2
2
2
2



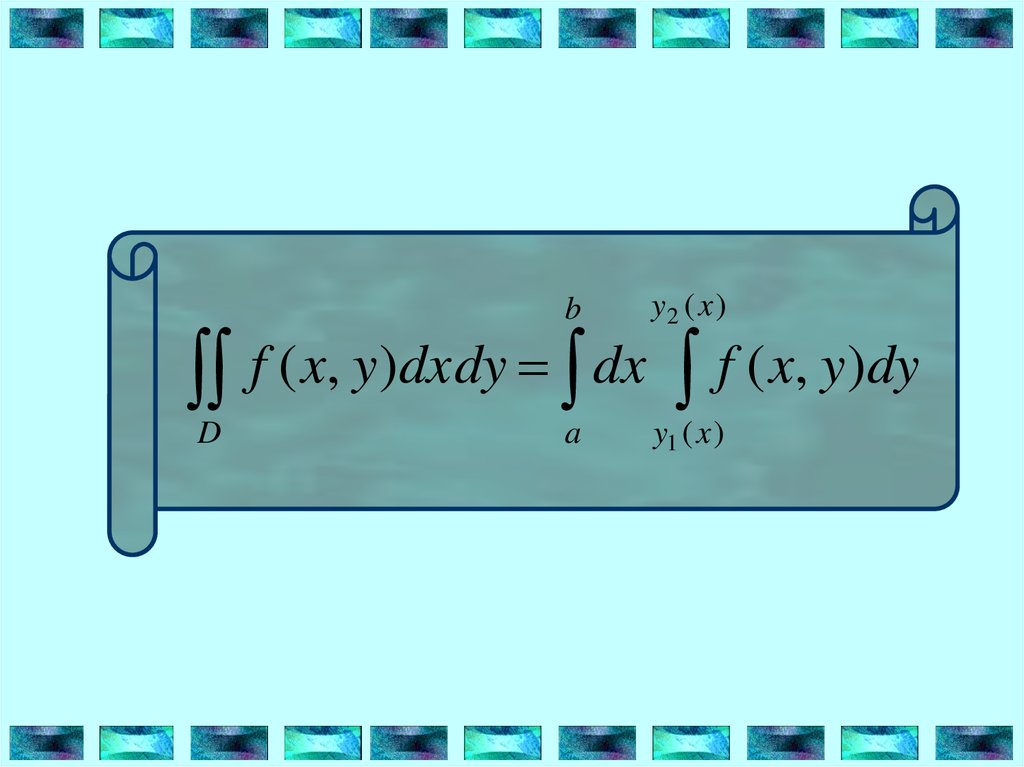






 mathematics
mathematics








