Similar presentations:
Применение метода рационализации при решении неравенств и систем неравенств
1. Применение метода рационализации при решении неравенств и систем неравенств
2.
Метод рационализациизаключается в замене сложного
выражения F(x) на более простое
выражение G(x), при котором
неравенство G(x)˃0 равносильно
неравенству F(x)˃0 в области
определения выражения F(x).
3.
Выражение F1
1а
1б
2
2а
2б
3
4
4а
5
6
Выражение G
4.
Теоретического обоснования методарационализации:
Если f(x) монотонно возрастающая функция и:
1. f(a) >f(b), то a>b;
2. f(a) - f(b) >o, то a-b>0.
3. f(a) - f(b) < o, то a-b< 0.
f ( x) f (b)
0
g ( x) g ( a )
4. Неравенство
можно
x b
заменить неравенством x a 0
которое можно решить методом
интервалов.
5.
Пример 1. Решите неравенство log 2x+3 x2 < 1.1.ОДЗ: 2 х 3 0,
2 x 3 1,
x 2 0.
3
; 1 1;0 0; .
2
2.Решим неравенство:
log 2x+3 x2 - 1 < 0.
lg x 2
lg x 2 lg( 2 x 3)
Перейдём к основанию 10: lg( 2 x 3) 1 0, lg( 2 x 3) 0,
lg x 2 lg( 2 x 3)
0
lg( 2 x 3) lg 1
x2 2x 3
0,
2x 3 1
Получим:(-∞; -1)U (-1; 3). Учтём ОДЗ.
ОТВЕТ. (-1,5; -1)U(-1; 0)U(0; 3).
6.
Пример 2. Решите неравенствоlog x2 x 1 x 2x 9 log x2 x 1 x 1
2
x 2 2 x 9 0,
2
x x 1 0,
2
x x 1 1,
x 1 0 /
1.ОДЗ
(1+
10
; +∞).
2
lg x 2 2 x 9
lg x 1
lg x 2 x 9 lg x 1
0
,
0,
2
lg x 2 x 1 lg x 2 x 1
lg x x 1
lg x 2 x 9 lg x 1
0,
2
lg x x 1 lg 1
2
x 2 3 x 10
0,
2
x x 2
x
2
2 x 9 x 1
0,
2
x x 1 1
(-∞;-2)U(-2;1)U[5;+∞) .
С учётом ОДЗ: [5;+∞).
7.
Решите неравенство1 3х 1
1. ОДЗ: 1 3 х 0, [-2;
1
2 х 1
2 х 0,
2 х 1 0.
1 3х 1
1 0, 1 3х 1 2 х 1 0
2 х 1
2 х 1
ПРИМЕР 3
1 3х 2 х
0,
2 х 1
1 3х 2 х
0,
2 х 1
С учётом ОДЗ: [-2;-1)U[- 1;
4
1
3
].
1
]
3
1
(-∞;-1)U[- 4;+∞).
8.
x40
ПРИМЕР 4 Решить систему неравенств log 6 x 2
x 12 x 36
х 1
х 2
25
0
,
5
2
х 2
0
,
5
,
х 2
х
Решим первое неравенство
2
4
ОДЗ: (-∞;-5)U(-5;0)U(0;6).
lg х 4 lg x 2 12 х 36
0,
lg 6 х lg 1
х 4 x 2 12 х 36
0,
6 х 1
[-3;2]U(5;+∞).
Решим второе неравенство
х 4 x 6
0,
5 x
25 2 х 1 2 х 2 х 2
2 0.
х 2
2х
2 2
2
25 2 х 1 2 х 2 20 2 х 2
х 1
0
log 25 ,то
Так
как
25
=2
25
2
2
2
0.
х 2
2х
0. получим:
х 2
2х
2 2
2 2
х 1 log 25
0
2
2
x 1 log 2 25
(-∞;2)U[log250;+∞)
0
.
0
.
х 2
2х
2 2
x 2 2x
2
Решение системы с учётом ОДЗ: [-3;0)U(0;2)U(5;6].
9.
Алгоритм1. Перенеси всё в левую часть.
2. Приведи к общему знаменателю, если это
нужно.
3. Если неравенство логарифмическое или
показательное, приведи его к одному
основанию.
4. Получи в числителе и знаменателе разность.
5.Замени неравенство на рациональное
6.Реши его.
7.Найди пересечение его решения с областью
определения.
10.
Пример 1.Решить неравенство:
ОТВЕТ: (-∞;-2)U(1;2)
11.
Пример 2.Решить неравенство:
Решение:
ОДЗ: (-1;1)
ОТВЕТ: (-1;0) U(0;1)
12.
Решить неравенства:Пример 3.
ОТВЕТ
Пример 4.
ОТВЕТ
Пример 5.
ОТВЕТ
Пример 6.
ОТВЕТ
13.
Пример 7.ОТВЕТ
Пример 8.
ОТВЕТ
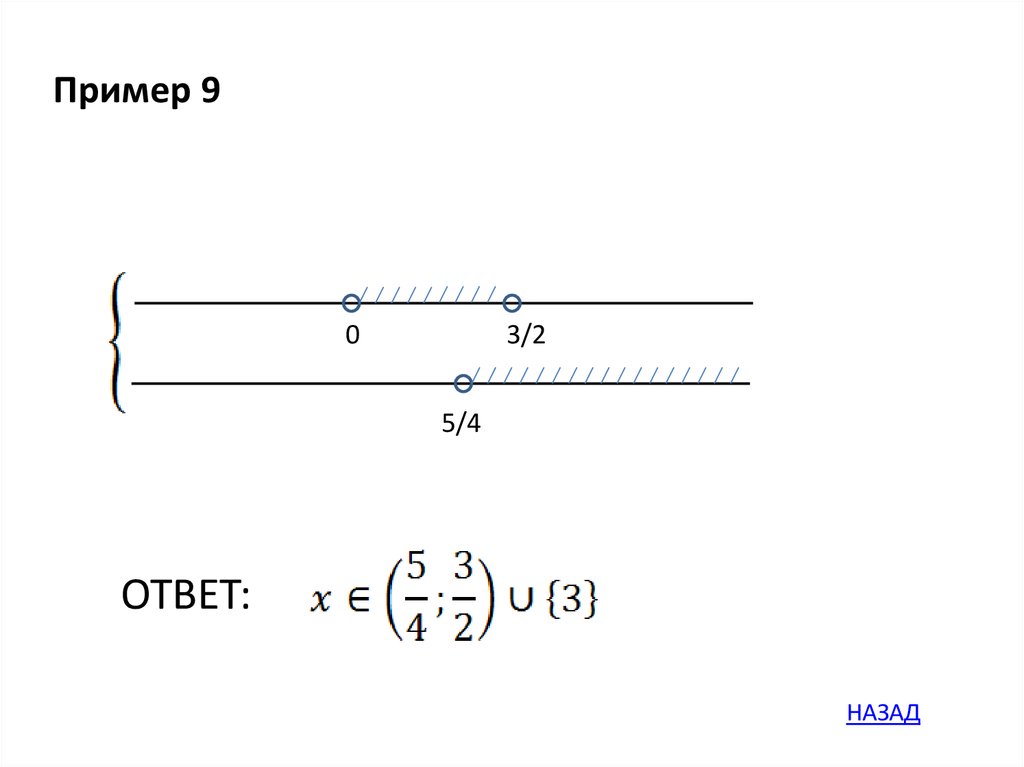
Пример 9.
ОТВЕТ
14.
Решить неравенство(из сборника МИОО):
15.
16.
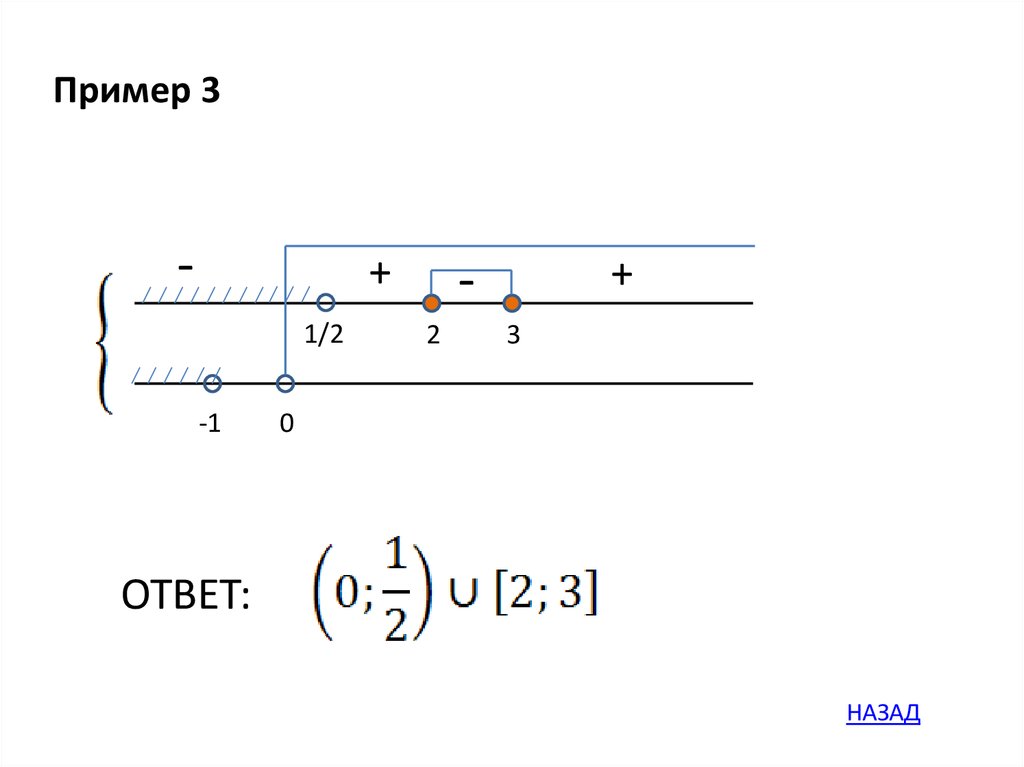
Пример 3-
+
1/2
-1
+
2
3
0
ОТВЕТ:
НАЗАД
17.
Пример 4+
1
-
+
+
6
2
3
9
ОТВЕТ:
НАЗАД
18.
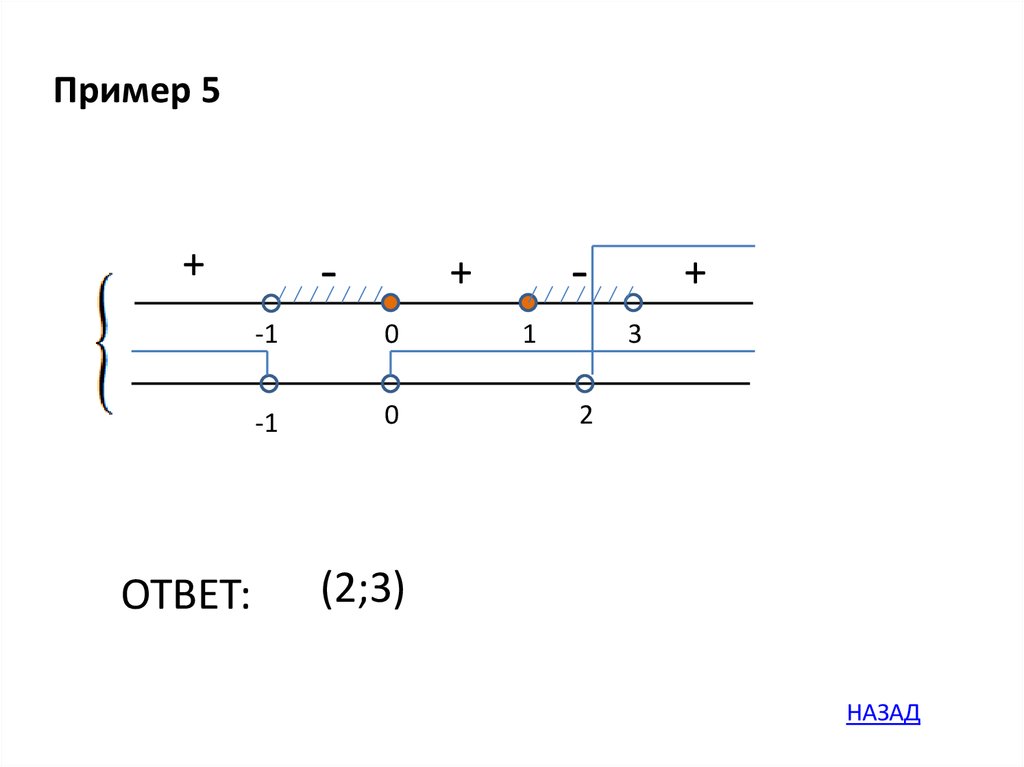
Пример 5+
ОТВЕТ:
-
-
+
-1
0
-1
0
1
+
3
2
(2;3)
НАЗАД
19.
Пример 6-
-
+
-2
-1
-1
+
1
0
ОТВЕТ:
НАЗАД
20.
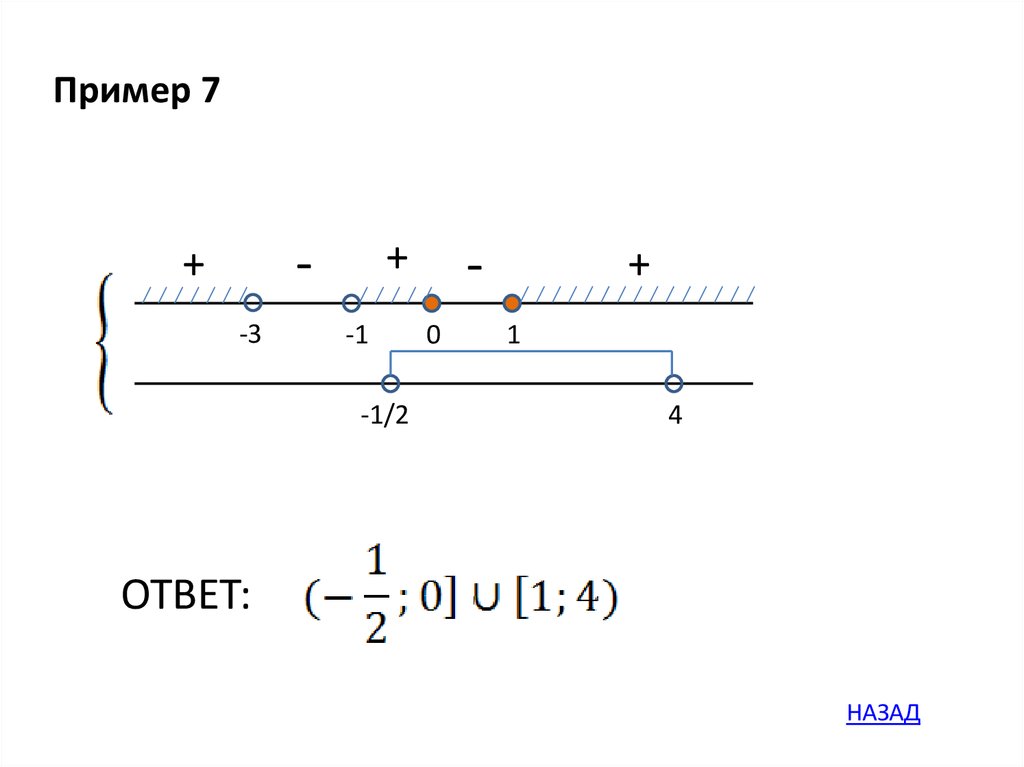
Пример 7+
-
+
-3
-1
-1/2
0
+
1
4
ОТВЕТ:
НАЗАД
21.
Пример 8+
+
-
3
1
1
+
2
ОТВЕТ:
НАЗАД
22.
Пример 90
3/2
5/4
ОТВЕТ:
НАЗАД














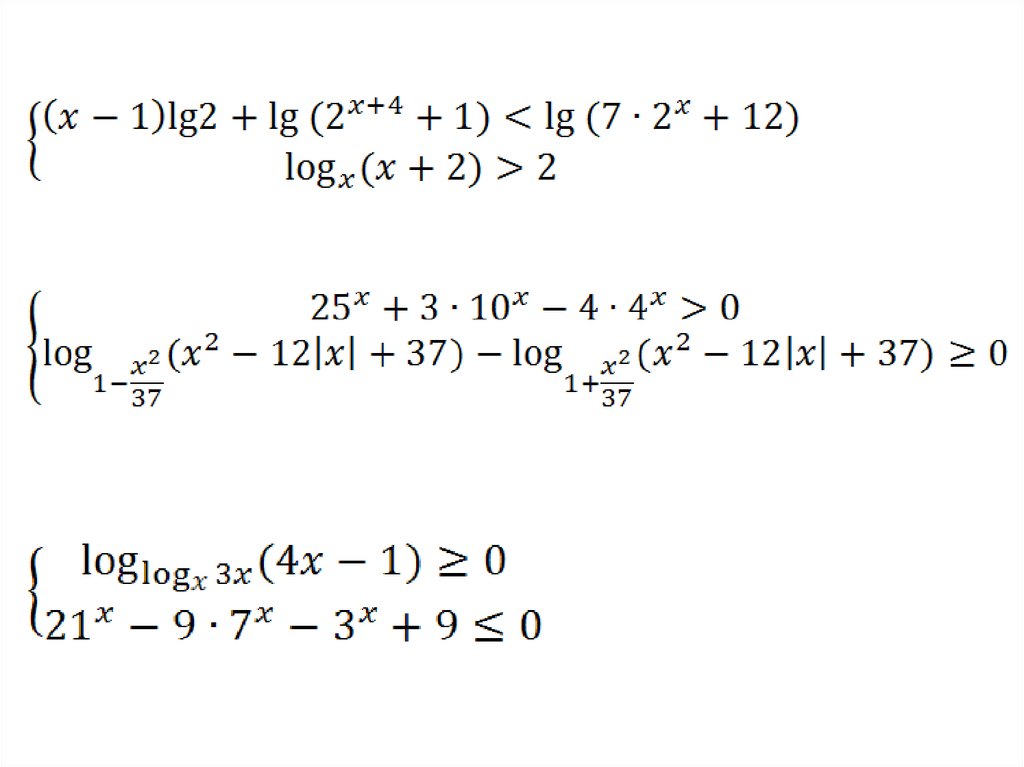



 mathematics
mathematics








