Similar presentations:
Решение рациональных неравенств методом интервалов
1. Решение рациональных неравенств методом интервалов.
МБОУ г. Мурманска гимназия №3Шахова Татьяна Александровна
2.
x 20
x
ОДЗ : х 0
Найди ошибку.
x 2
0 x 0
x
x 2 0
Свойства числовых неравенств
позволяют нам умножать
(делить) обе части неравенства
на число, о котором точно
известно, что оно строго больше
нуля (знак неравенства не
меняется) или строго меньше
нуля (знак неравенства меняется
на противоположный).
Про х в данном случае таких
данных мы не имеем.
x 2
Легко убедится, что
неравенство решено
неверно:
x = -2 является
решением
первоначального
Как решать?
неравенства, но не Один из способов решения рациональных
удовлетворяет
неравенств (метод интервалов) основан на
неравенству х >2. свойствах функций.
17.01.2020
2
3.
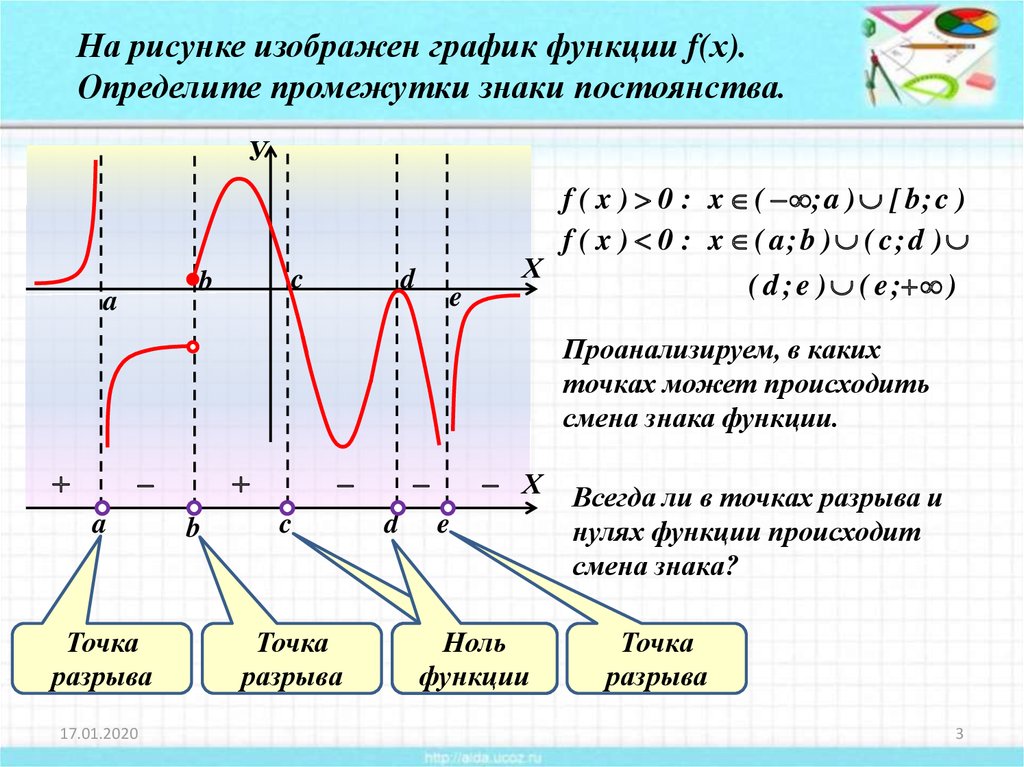
На рисунке изображен график функции f(х).Определите промежутки знаки постоянства.
У
c
b
a
Х
d
f ( x ) 0 : x ( ; a ) [ b ; c )
f ( x ) 0 : x ( a; b ) ( c ; d )
( d ; e ) ( e ; )
e
Проанализируем, в каких
точках может происходить
смена знака функции.
a
Точка
разрыва
17.01.2020
b
c
Точка
разрыва
d
Х
e
Ноль
функции
Всегда ли в точках разрыва и
нулях функции происходит
смена знака?
Точка
разрыва
3
4.
Решение неравенств методом интервалов.Алгоритм.
У
Для решения неравенств вида
f ( x ) 0( 0 , 0 , 0 )
можно воспользоваться схемой:
Х 1) найти D(f) (точки разрыва –
e
a
нули знаменателя);
2) найти нули функции (нули
числителя);
3) на числовую прямую нанести
область определения и нули
Х функции. Нули функции и точки
a
c
d e
b
разрыва разбивают ее область
определения на промежутки, в каждом из которых функция сохраняет
постоянный знак;
4) определить знаки функции в полученных промежутках, вычислив
значение функции в какой-либо одной точке из каждого промежутка
или воспользовавшись правилом чередования знаков;
Назад4
5) записать ответ.
b
c
d
5.
Правило чередования знаков.(используется, если левая часть неравенства
разложена на множители )
Правило чередования знаков значительно облегчает определение
знаков функции на числовых промежутках.
Основано на том что неотрицательный множитель не влияет на
знак произведения.
( x a )2 n 1 множитель нечетной степени
а
х а корень нечетной кратности
а
При переходе через корень нечетной кратности знак меняется.
!
c
!
c
При переходе через корень четной кратности знак не меняется.
( x c )2 n множитель четной степени
(неотрицательный)
х c корень четной кратности
Таким образом достаточно подстановкой определить знак на
любом промежутке и воспользоваться данным правилом.
Назад
17.01.2020
5
6.
Пример: для функцииа) f(x)>0,
3
2 x ( x 4 )8
f(x)
определите при каких х
x2 ( 6 x )
в) f(x)≥0,
г) f(x)≤0.
б) f(x)<0,
1) Нули знаменателя: х ( 6 x ) 0
знаменателя
четной кратности
х 2 0 х 0 - корень
изображаются
на числовой
прямой
всегда выколотыми
знаменателя
нечетной кратности
6 x 0 х 6 - корень
точками
2) Нули числителя: ( 2 x )3 ( x 4 )8 0
( 2 x )3 0 х 2 - корень
числителя
нечетной
кратности
изображаются
точками
в
числителя
четной кратности
зависимости
от знака
( x 4 )8 0 х 4 - корень
2
3)
-6
!
-4
неравенства
!
0
2
4) Определим знак на любом промежутке.
Например, на крайнем правом х=100
Далее воспользуемся правилом чередования знаков.
5)
Алгоритм
17.01.2020
Правило
6
7.
Пример: для функцииа) f(x)>0,
5)
а) f(x)>0
б) f(x)<0
г) f(x)≤0
Алгоритм
17.01.2020
x2 ( 6 x )
в) f(x)≥0,
г) f(x)≤0.
б) f(x)<0,
-6
-6
-6
!
!
!
-4
!
!
!
0
!
0
2 x ( ; 6 ) ( 2 ; )
0
2 x ( 6 ; 4 ) ( 4 ;0 ) ( 0 ;2 )
0
-4
-4
!
-4
-6
в) f(x)≥0
3
2 x ( x 4 )8
f(x)
определите при каких х
2
x ( 6 ;0 ) ( 0 ;2 ]
2
x ( ; 6 ) { 4 } [ 2 ; )
Правило
7
8.
Метод интервалов – это универсальный способ решенияпрактически любых неравенств, которые встречаются в
школьном курсе алгебры.
Рассмотрим решение рациональных неравенств данным методом.
Рациональным называется неравенство вида Q( x ) 0( 0 , 0 , 0 )
P( x )
где Q(x) и P(x) – рациональные выражения.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
17.01.2020
8
9.
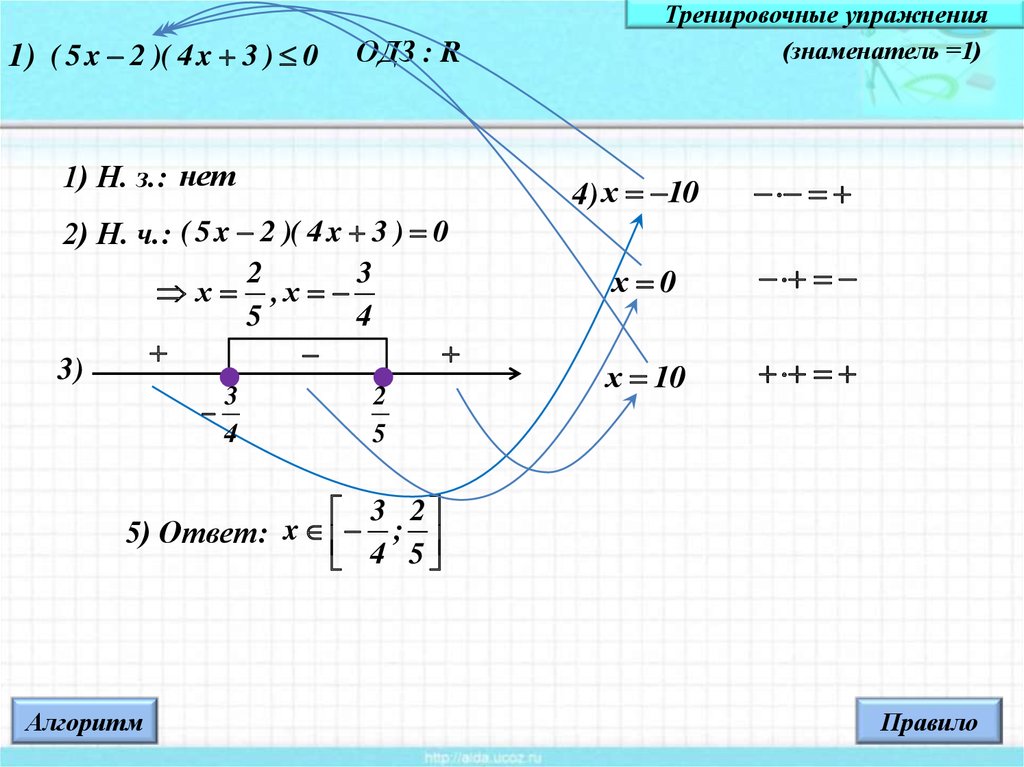
1) ( 5 x 2 )( 4 x 3 ) 0ОДЗ : R
1) Н. з.: нет
2) Н. ч.: ( 5 x 2 )( 4 x 3 ) 0
2
3
х ,х
5
4
3)
3
4
2
5
Тренировочные упражнения
(знаменатель =1)
4) х 10
х 0
х 10
3 2
x
5) Ответ:
4 ; 5
Алгоритм
17.01.2020
Правило
9
10.
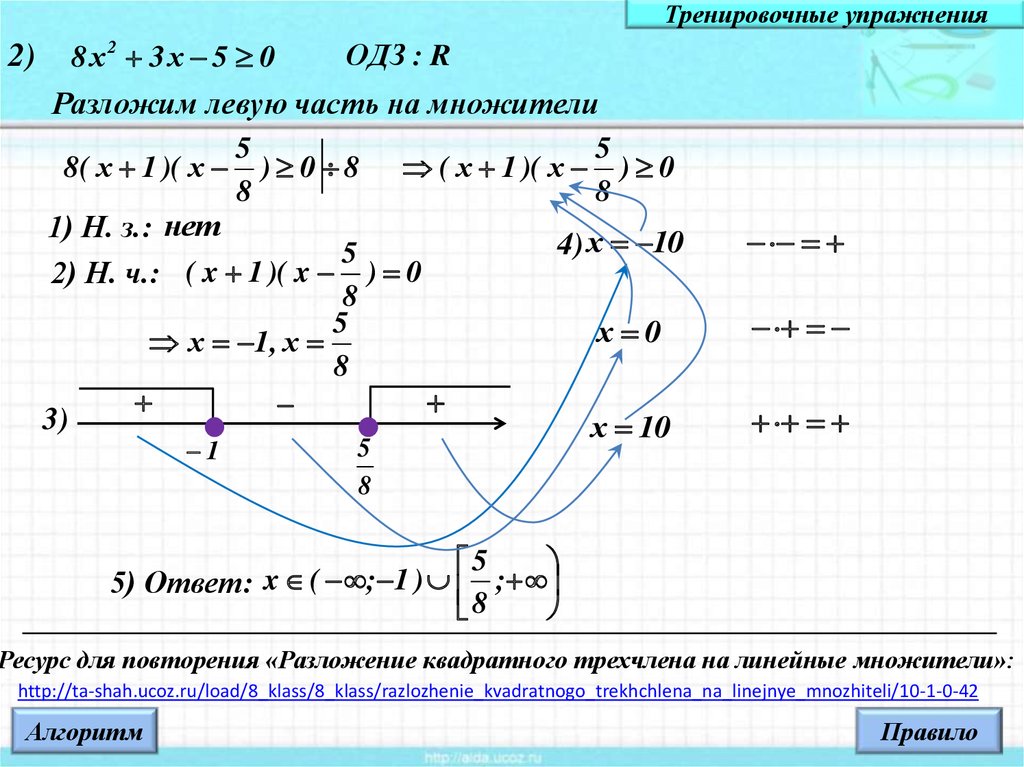
Тренировочные упражнения2)
8 х2 3 х 5 0
ОДЗ : R
Разложим левую часть на множители
5
5
8( х 1 )( х ) 0 8 ( х 1 )( х ) 0
8
8
1) Н. з.: нет
4) х 10
5
2) Н. ч.: ( x 1 )( x ) 0
8
5
х 0
х 1, х
8
3)
х 10
1
5
8
5
x
(
;
1
)
;
5) Ответ:
8
Ресурс для повторения «Разложение квадратного трехчлена на линейные множители»:
http://ta-shah.ucoz.ru/load/8_klass/8_klass/razlozhenie_kvadratnogo_trekhchlena_na_linejnye_mnozhiteli/10-1-0-42
17.01.2020
Алгоритм
10
Правило
11.
Тренировочные упражненияОДЗ : R
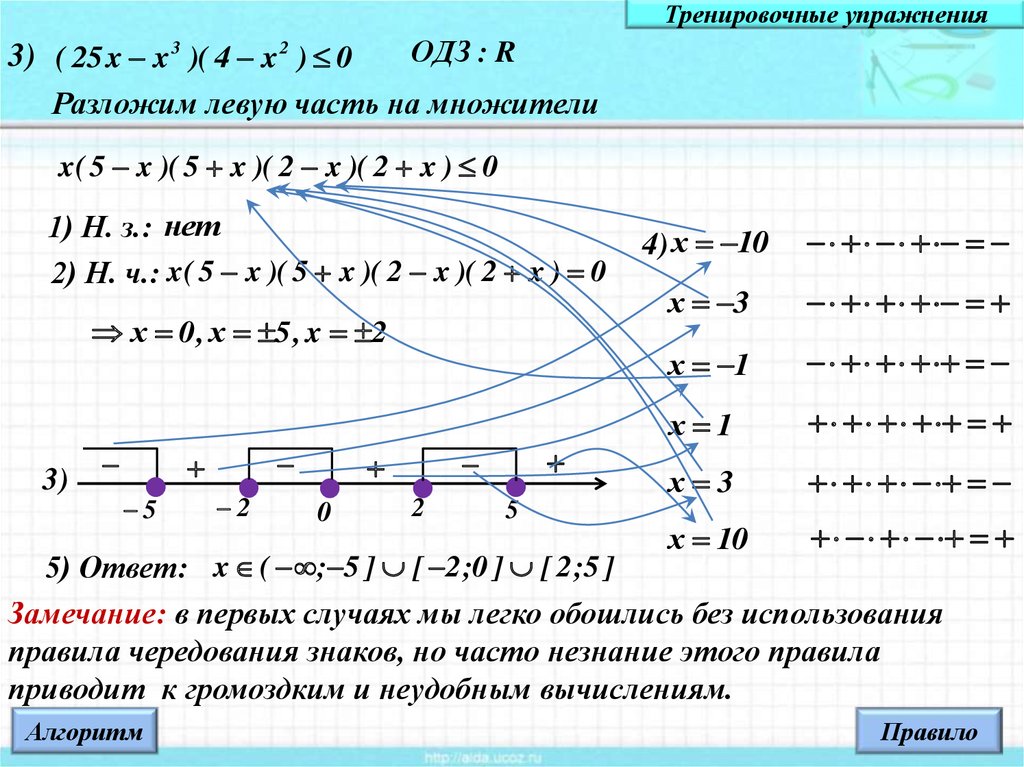
3) ( 25 x x 3 )( 4 x 2 ) 0
Разложим левую часть на множители
x( 5 x )( 5 x )( 2 x )( 2 x ) 0
1) Н. з.: нет
2) Н. ч.: x( 5 x )( 5 x )( 2 x )( 2 x ) 0
х 0 , х 5 , x 2
3)
5
2
0
2
5
4) х 10
х 3
х 1
х 1
х 3
х 10
5) Ответ: x ( ; 5 ] [ 2 ;0 ] [ 2 ;5 ]
Замечание: в первых случаях мы легко обошлись без использования
правила чередования знаков, но часто незнание этого правила
приводит к громоздким и неудобным вычислениям.
17.01.2020
Алгоритм
11
Правило
12.
Тренировочные упражнения4) ( х 2 5 х 2 )( 3 x 2 x 5 ) 0
Разложим левую часть на множители
ОДЗ : R
5 33
5 33
1 61
1 61
x
x
x
x
0
2
2
6
6
(все множители имеют нечетную (первую) степень => корней четной кратности нет)
1) Н. з.: нет
2) Н. ч.: x
3)
5 31
1 61
,x
2
6
5 31
2
1 61
6
Как сравнить?
5 31
2
1 61
6
Правило
Определим знак на любом промежутке.
Алгоритм
Например, на крайнем правом х=1000
5 31 1 61 5 31 1 61
;
;
5) Ответ: x
2
6
2
6
При решении следующих неравенств будем закреплять умение
пользоваться правилом чередования знаков.
13.
5)2 x 0
x
2
Тренировочные упражнения
ОДЗ : х 0
1) Н. з.: х 2 0 х 0 - корень четной кратности
2) Н. ч.: 2 х 0 х 2
3)
!
0
2
4) Определим знак на любом промежутке.
Например, на крайнем правом х=1000
2 1000
1000 2
5) Ответ: x ( ;0 ) ( 0 ;2 ]
Алгоритм
17.01.2020
Правило
15
14.
Тренировочные упражнения6) ( х 1 )2 ( x 2 2 ) ( x 1 )2 ( 6 2 x )
Приведем неравенство к виду f(x)≥0
ОДЗ : R
( х 1 )2 ( x 2 2 ) ( x 1 )2 ( 6 2 x ) 0
Разложим левую часть на множители
( х 1 )2 (( x 2 2 ) ( 6 2 x )) 0 ( х 1 )2 ( x 2 2 x 8 ) 0
( х 1 )2 ( x 4 )( x 2 ) 0
1) Н. з.: нет
Удовлетворяет
кратности
2) Н. ч.: x 1 - корень четной
неравенству
x 4
x 2
!
3)
4
1
2
При решении
нестрогого
неравенства
нули числителя
проверяем особо!
4)Определим знак на любом промежутке.
Например, на крайнем правом х=1000
5) Ответ: x ( ; 4 ] { 1 } [ 2 ; )
Алгоритм
Правило
15.
Тренировочные упражнения7) x 4 13 x 2 36
Приведем неравенство к виду f(x)≥0
ОДЗ : R
x 4 13 x 2 36 0
Разложим левую часть на множители
( x 2 4 )( x 2 9 ) 0 ( x 2 4 )( x 3 )( x 3 ) 0 ( x 2 4 ) 0
( x 3 )( x 3 ) 0
1) Н. з.: нет
2) Н. ч.: x 3
3)
3
3
4)Определим знак на любом промежутке.
Например, на крайнем правом х=1000
5) Ответ:
Алгоритм
x ( ; 3 ] [ 3 ; )
Правило
16.
Тренировочные упражнения8) ( x 9 )( 1 x ) 0
2
2
3
ОДЗ : х 1, x 5
5 4x x
Разложим левую часть на множители
( x 3 )( x 3 )( 1 x )3
0
( x 1 )( x 5 )
Обрати внимание: сокращение дроби в
данном случае не является равносильным
преобразованием, так как изменяет ОДЗ.
( x 3 )( x 3 )( 1 x )2
0
( x 5)
1) Н. з.: х 5
2) Н. ч.: х 3
x 1 - корень четной кратности
3)
3
1
3
Правило
5
4) Определим знак на любом промежутке.
Например, на крайнем правом х=1000
5) Ответ: x [ 3 ; 1 ) ( 1;3 ] ( 5 ; )
17.01.2020
Алгоритм
18
17.
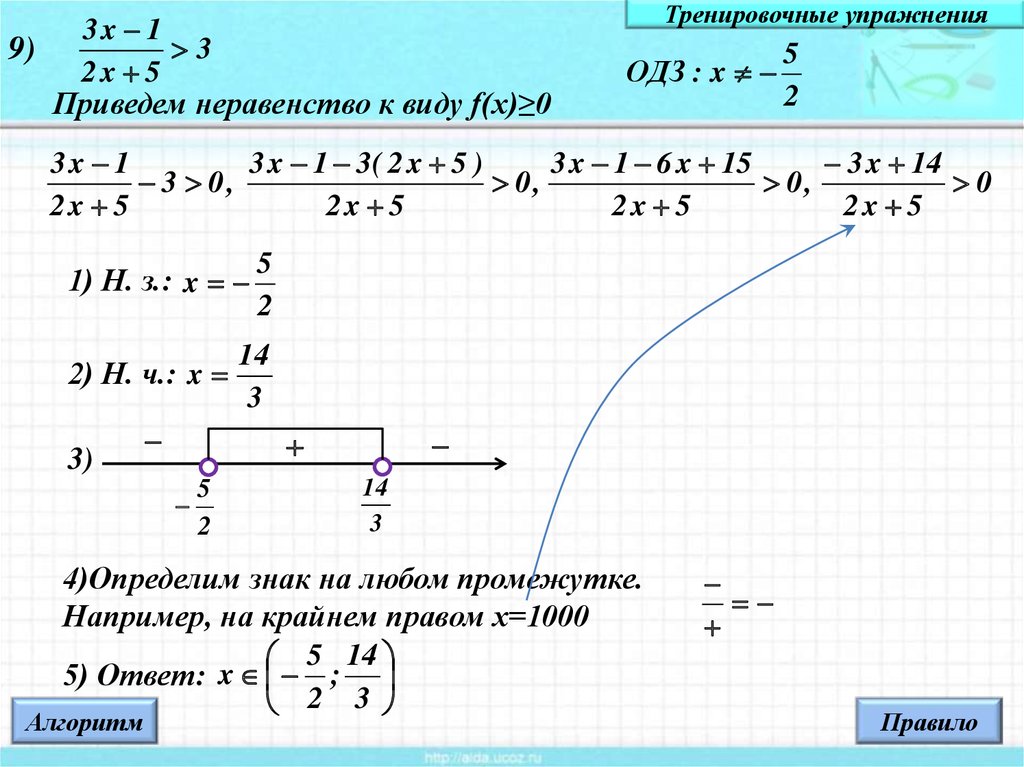
3x 13
9)
2x 5
Приведем неравенство к виду f(x)≥0
Тренировочные упражнения
ОДЗ : x
5
2
3x 1
3 x 1 3( 2 x 5 )
3 x 1 6 x 15
3 x 14
3 0,
0,
0,
0
2x 5
2x 5
2x 5
2x 5
1) Н. з.: x
2) Н. ч.: x
3)
5
2
14
3
5
2
14
3
4)Определим знак на любом промежутке.
Например, на крайнем правом х=1000
5 14
5) Ответ: x ;
2 3
Алгоритм
Правило
18.
Тренировочные упражнения1
10) 3 x
2 x
Приведем неравенство к виду f(x)≥0
ОДЗ : x 2
2
1
(
3
x
)(
2
x
)
1
x
5x 5
3 x
0,
0,
0,
2 x
2 x
2 x
Разложим левую часть
на множители
5 5
5 5
x
x
2
2
0,
2 x
1) Н. з.: x 2
2) Н. ч.: x
3)
5 5
2
4)Определим знак на любом промежутке.
Например, на крайнем правом х=1000
5 5 5 5
2;
5) Ответ: x ;
2
2
Алгоритм
5 5
2
2
5 5
2
Правило
19.
x 2 8 x 16 8 x 2 x 22
11) x 2
x 2x 1
x 1
Приведем неравенство к виду f(x)≥0
2
2
x
8
x
16
8
x
2
x
x2
0
2
( x 1)
x 1
Упростим
и разложим
левуюплюс
Квадрат первого
выражения
квадрат
второго плюс удвоенное
часть
на множители
2
x 2 ( x произведение
1 )2 ( x 4 )первого
2 x( 4на второе.
x )( x 1 )
0
2
( x 1)
x 2 ( x 1 )2 ( x 4 )2 2 x( x 4 )( x 1 )
0
2
( x 1)
( x( x 1 ) ( x 4 ))2
0
2
( x 1)
( x 2 4 )2
0
2
( x 1)
( x 2 )2 ( x 2 )2
0
2
( x 1)
Алгоритм
Тренировочные упражнения
ОДЗ : x 1
( x 2 )2 ( x 2 )2
0
2
( x 1)
Левая часть не может
принимать отрицательные
значения =>
решениями неравенства
являются нули числителя.
Ответ:
x 2 2
Правило
20.
x 4 5 x 3 5 x 251
5
2
12)
x
x2 5 x
x 4 x
Приведем неравенство к виду f(x)≥0
x 4 5 x 3 5 x 25
1
5
2
x
0
2
x 5x
x 4 x
Упростим и разложим левую
часть на множители
x 3 ( x 5 ) 5( x 5 )
1
5
x2
0
x( x 5 )
x 4 x
( x 3 5 )( x 5 )
1
5
2
x
0
x( x 5 )
x 4 x
x 5
1
5
x2
0
x
x 4 x
3
x3 5
1
5
2
x
0
x x
x 4 x
1
x2 x2
0
x 4
Тренировочные упражнения
ОДЗ : x 0 , x 5 , x 4
1
0
x 4
Алгоритм
1) Н. з.: x 4
Правило
2) Н. ч.: нет
3)
0
4
5
4)Определим знак на любом
промежутке. Например,
на крайнем правом х=1000
Учтем ОДЗ
5) Ответ: x ( 4 ;5 ) ( 5 ; )
21.
13) x 5 x2 3 x 25 x 24
3
1
5
x 5x
x 4 x
Приведем неравенство к виду f(x)≥0
Тренировочные упражнения
ОДЗ : x 0 , x 5 , x 4
x 4 5 x 3 3 x 25
1
5
2
x
0
2
x 5x
x 4 x
Решение данного неравенства «в лоб» приведет к появлению больших
степеней. Используем следующий прием: 3х = 5х-2х.
( x 4 5 x 3 ) ( 5 x 25 ) 2 x
1
5
2
x
0
2
x 5x
x 4 x
x 3 ( x 5 ) 5( x 5 )
2x
1
5
2
x
0
x( x 5 ) x( x 5 ) x( x 5 )
x 4 x
5
2
1
5
x2
x2
0
x x 5
x 4 x
2
1
2( x 4 ) ( x 5 )
3 x
0,
0,
0,
x 5 x 4
( x 5 )( x 4 )
( x 5 )( x 4 )
Алгоритм
Правило
22.
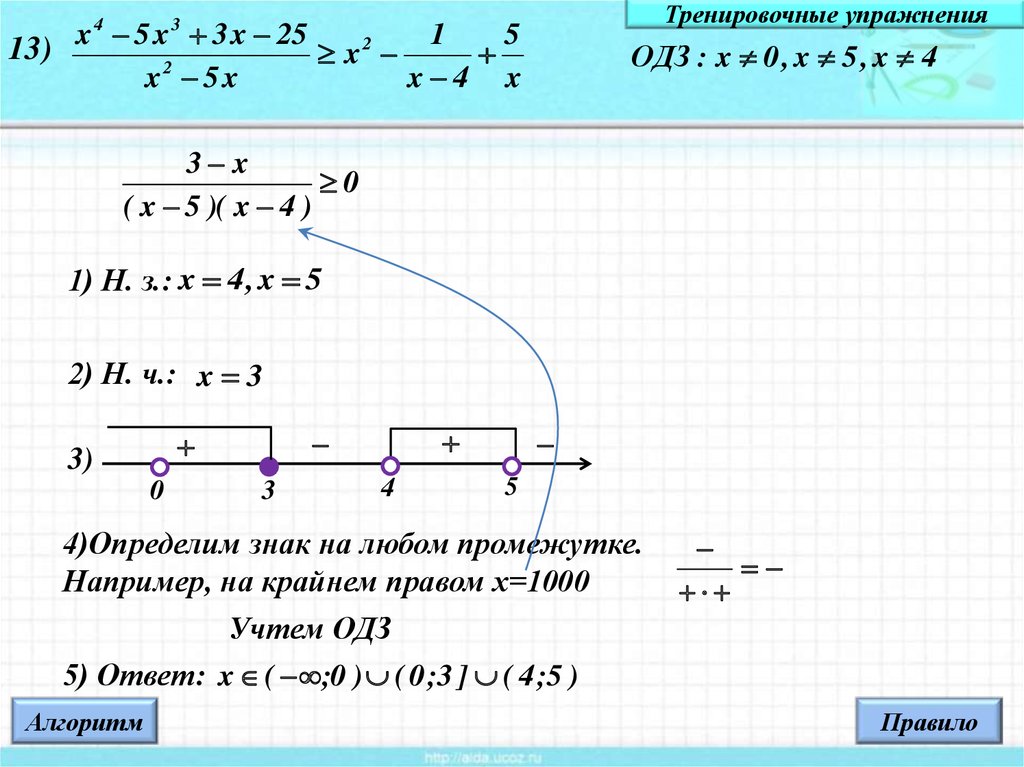
13) x 5 x2 3 x 25 x 24
3
x 5x
Тренировочные упражнения
1
5
x 4 x
ОДЗ : x 0 , x 5 , x 4
3 x
0
( x 5 )( x 4 )
1) Н. з.: x 4 , x 5
2) Н. ч.: x 3
0
3)
3
4
5
4)Определим знак на любом промежутке.
Например, на крайнем правом х=1000
Учтем ОДЗ
5) Ответ: x ( ;0 ) ( 0 ;3 ] ( 4 ;5 )
Алгоритм
Правило
23.
14)Тренировочные упражнения
50 x x 7
1
x 7
Приведем неравенство к виду f(x)≥0
x3 8 x2
2
50 x x 7
1 0
x 7
Преобразуем левую часть
x3 8 x2
2
50 x 2 x 7
x 8x
1 0
x 7 x 7
3
2
50 x 2
x 8x
1 1 0
x 7
( x 3 8 x 2 )( x 7 ) 50 x 2
0
x 7
x4 x3 6 x2
0
x 7
3
2
x2 ( x2 x 6 )
0
x 7
ОДЗ : x 7
Алгоритм
x 2 ( x 3 )( x 2 )
0
x 7
Правило
1) Н. з.: x 7
2) Н. ч.: x 2 , x 3
x 0 - корень
четной кратности
3)
3
!
0
2
7
4)Определим знак на любом
промежутке. Например,
на крайнем правом х=1000
5) Ответ: x ( ; 3 ] { 0 } [ 2 ;7 )
24.
15)Тренировочные упражнения
1
2x 6 x 1
12
2x
ОДЗ
:
x
3
,
x
5 x 12
x 3
5
Приведем неравенство к виду f(x)≥0
2
1
2 x2 6 x 1
2x 0
5 x 12
x 3
Преобразуем левую часть
1
2 x( x 3 )
1
2x 0
5 x 12
x 3
x 3
1
1
2x
2x 0
5 x 12
x 3
1
1
0
5 x 12 x 3
6 x 15
0
( 5 x 12 )( x 3 )
12
x
3
,
x
1) Н. з.:
5
5
2) Н. ч.: x
2
3)
12
5
5
2
3
4)Определим знак на любом
промежутке. Например,
на крайнем правом х=1000
( x 3 ) ( 5 x 12 )
0
( 5 x 12 )( x 3 )
Правило
12 5
x
; ( 3 ; )
5) Ответ:
Алгоритм
5 2
25.
Источники:М. Л. Галицкий, А. М. Гольдман, Л. И. Звавич
«Сборник задач по алгебре 8-9»
КИМ ЕГЭ 2013г.
http://alexlarin.net/ege/2013/c3_2013.html



















 mathematics
mathematics








