Similar presentations:
Решение неравенств методом интервалов
1.
РЕШЕНИЕ НЕРАВЕНСТВМЕТОДОМ ИНТЕРВАЛОВ
2.
Решаем неравенства:1.
7 x 4 4x 8
3.
Решаем неравенства:1.
7 x 4 4x 8
x 4
-4
Ответ:
х
; 4
4. 5х + 3(2х – 1)>13х - 1
2.5х + 3(2х – 1)>13х - 1
5. 5х + 3(2х – 1)>13х - 1
2.5х + 3(2х – 1)>13х - 1
Решение: 5х + 6х – 3 >13х – 1
5х + 6х – 13х > 3 – 1
-2х > 2 (: (-2))
х < -1
-1
\\\\\\\\\\\\\\\\\
Ответ: (-∞; -1)
x
6.
Решения неравенств методоминтервалов
(х+4)(х-2)(х-3)<0
7.
Алгоритм решения неравенствметодом интервалов
• Разложить многочлен на простые
множители;
• Найти корни многочлена;
• Изобразить их на числовой прямой;
• Разбить числовую прямую на интервалы;
• Определить знаки множителей на
интервалах знакопостоянства;
• Выбрать промежутки нужного знака;
• Записать ответ (с помощью скобок или
знаков неравенства).
8.
(10х+3)(17-х)(х-5)≥09.
Решения неравенствметодом параболы
(5-х)(х+6)<0
методом интервалов
(5-х)(х+6)<0
10.
ВЫВОД: Решения неравенствметодом параболы
методом интервалов
(5-х)(х+6)<0
(5-х)(х+6)<0
(-х²-х+30)<0
11.
Самостоятельная работаВариант 1.
Вариант 2.
Решите неравенства методом
интервалов:
12.
Проверь своё решениеВариант 1.
Вариант 2.
а) (2 x 5)( x 3) 0;
–
+
-3
Ответ:
а) (5 x 2)( x 4) 0;
+
x
2,5
; 3 2,5; .
б) 4 x 2 4 x 3 0.
–
+
-3/2
3 1
Ответ: ;
2 2
-4
+
x
0,4
Ответ: 4;0,4
б) 9 x 2 3x 2 0.
+
1/2
–
+
–
+
x
-2/3
+
1/3
2
Ответ: ;
3
x
1
3 ; .
13.
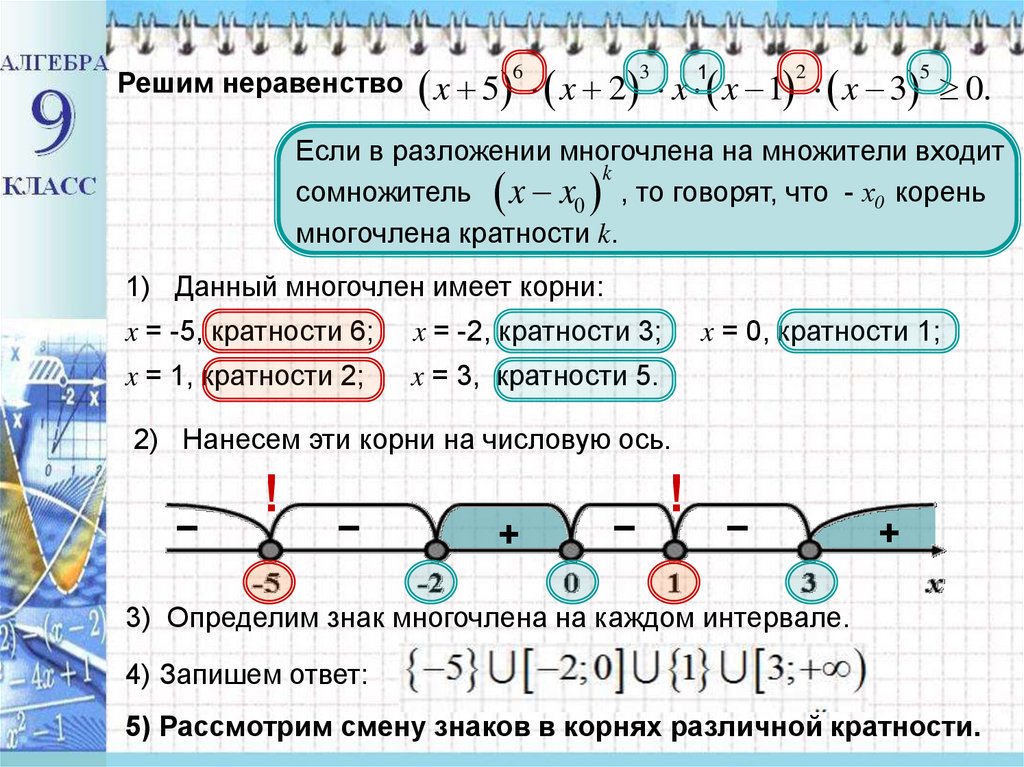
Решим неравенствоx 5 x 2 x x 1 x 3 0.
6
3
2
1
5
Если в разложении многочлена на множители входит
k
сомножитель x x0 , то говорят, что - х0 корень
многочлена кратности k.
1) Данный многочлен имеет корни:
x = -5, кратности 6;
x = -2, кратности 3;
x = 1, кратности 2;
x = 3, кратности 5.
x = 0, кратности 1;
2) Нанесем эти корни на числовую ось.
–
!
–
+
–
!
–
+
3) Определим знак многочлена на каждом интервале.
4) Запишем ответ:
x 5
2;0 1 3; .
5) Рассмотрим смену знаков в корнях различной кратности.
14.
Обобщая ваши наблюдения, делаем выводы:Для решения неравенства важно
знать, является ли k четным или
нечетным числом
При четном k многочлен справа и
слева от х0 имеет один и тот же
знак (знак многочлена не меняется)
При нечетном k многочлен справа и
слева от х0 имеет противоположные
знаки (знак многочлена изменяется)
15.
Решите неравенство1 вариант:
x 3 x 2 x 7 x 10 0.
4
5
2
2 вариант:
x 9 x 2 x 6 x 1 0.
2
5
3
Сделайте выводы о смене знака
на интервалах, в зависимости от
степени кратности корня.



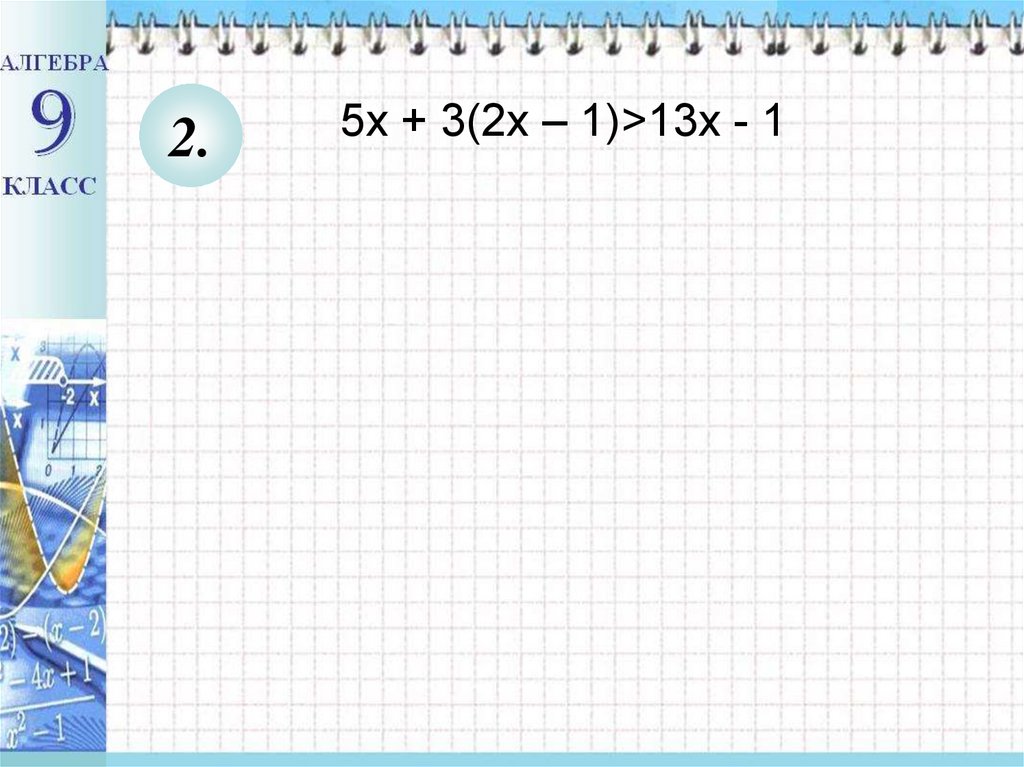










 mathematics
mathematics








