Similar presentations:
Метод рационализации. Решение задания №17. Подготовка к ЕГЭ 2019 по математике
1.
Подготовка к ЕГЭ 2019по математике
Решение задания №17.
Метод рационализации.
Учитель математики Лемехова Г.М.
Г. Северодвинск
2.
Суть метода.Метод рационализации
(декомпозиции, метод замены
множителей, правило знаков)
заключается в замене сложного
выражения F(x) на более простое
выражение G(х) (в конечном итоге
рациональное), при которой
неравенство G(х) v 0 равносильно
неравенству F(x) v 0 в области
определения выражения F(x).
3.
ДекомпозицияДекомпозиция — это научный метод,
использующий структуру задачи и
позволяющий заменить решение
одной большой задачи решением
серии меньших задач, пусть и
взаимосвязанных, но более простых.
( Разделение целого на части)
4.
Метод широко используется прирешении неравенств с переменным
основанием логарифма и позволяет
решать неравенства такого вида без
перехода
к
равносильной
совокупности
систем,
решение
которой
является
достаточно
трудоёмким и требующим большого
количества времени.
5.
Алгоритм метода рационализации1. ОДЗ
2.Привести к виду
3. Заменить все выражения ,… на более
простые.
4. Решить полученное неравенство.
5. Выписать ответ.
6.
Метод рационализации влогарифмических неравенствах
7.
loga f ( x) loga g ( x) 0, a 0, a 1.Знак «сохраняется».
log a f ( x ) log a g ( x ) 0
( a 1)( f ( x ) g ( x )) 0,
f ( x ) 0,
g ( x ) 0.
8.
1) loga f ( x) 0, a 0, a 1.log a f ( x) log a 1.
Знак
«сохраняется».
(a 1) ( f ( x) 1) 0,
log a f ( x) 0
f ( x) 0.
9.
log a ( x ) f ( x) log a ( x ) g ( x) 0,log a ( x ) f ( x) log a ( x ) g ( x) 0
(a ( x) 1)( f ( x) g ( x)) 0,
a ( x) 0,
a ( x) 1,
f ( x) 0,
g
(
x
)
0
.
10.
log a ( x ) f ( x) 0.log a(x) f(x) 0
(а( х) 1) (
a( x) 0,
a( x) 1,
f
(
x
)
0
;
f ( x) 1) 0,
11.
Решите неравенство: 1).log 1 5 x 1 2
2
Применим метод равносильного перехода:
1
5 x 1 0,
x
,
5
5
x
1
4
x 1
1
;1 .
5
12.
Проведём рационализацию , представив 2 в1
виде логарифма с основанием
2
5 x 1 0,
log 1 5 x 1 log 1 4 1
1
5
x
1
4
0
2
2
2
1
x ,
5
x 1.
Ответ:
1
x 1.
5
13.
log2
x
13
x
20
1
2
2).
0
log 3 x 7
2
log 2 2 x 13x 20 log 2 2
0
log 3 x 7
2
14.
log 2 2 x 13x 20 log 2 20
log 3 x 7
2
5
2 x 4 x 0,
2 x 2 13x 20 0,
2
x 7 0,
x 7,
2 1 2 x 2 13x 20 2
9
0; x 2 x
3 1 x 7 1
2 0.
2 x 6
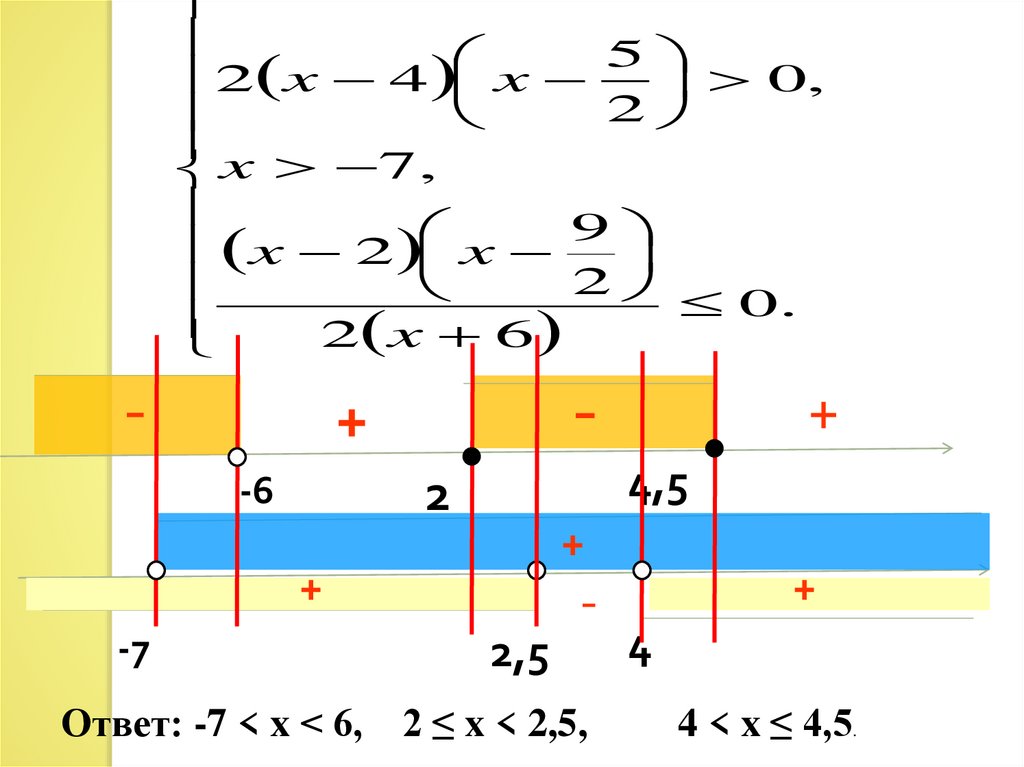
15.
52 x 4 x
0,
2
x 7 ,
9
x 2
x
2
0.
2 x 6
-
-
+
4,5
2
-6
+
+
-7
Ответ: -7 < x < 6,
+
2,5
2 ≤ x < 2,5,
+
4
4 < x ≤ 4,5.
16.
3). log 0,1 x x 2 log 0,1 x 3 .2
0,1 1 x x 2 x 3 0,
2
x x 2 0,
x 3 0
Ответ:
2
5 ; 2 1; 5 .
17.
log 2 3 x 24).
0.
log 2 2 x 3
x
2 1 3x 1
0
,
x
2 1 2 x 2
3x 2 0,
x
2 x 3 0
x
1,
2
1
x
,
,
3
3
1
2
x .
,
3
3
1,5
2
1
Ответ: x .
3
3
18.
x 45).
0;
2
log 1 x 1
2
2
2 1 2
2
2
x 4 1 x 2 0, x 4 x 2 0,
2
2
x 1 0
x2 1 0
Ответ:
; 2
2 ; 1 1; 2 2; .
19.
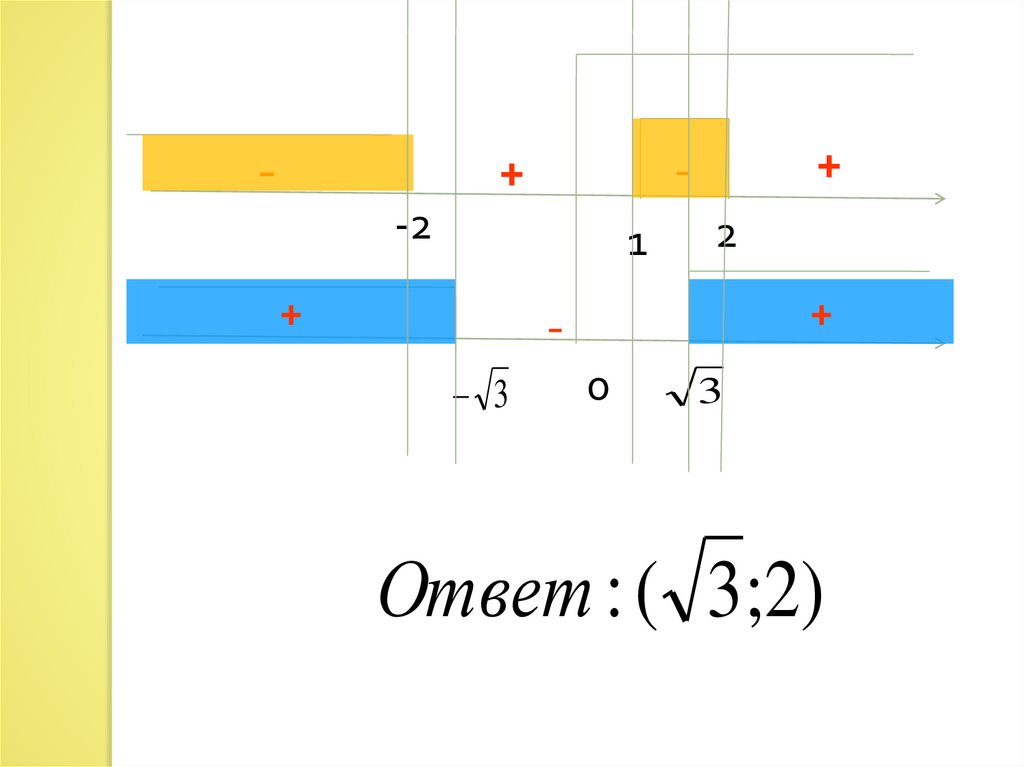
log a ( x ) f ( x) log a ( x ) g ( x) 0,20.
-+
-2
1
+
+
2
+
3
0
3
Ответ : ( 3;2)
21.
22.
23.
6).lg 4 y
log
log
5 y 1
lg 5 y 2 y 1
2
2
53
7
5
7
3
2
lg
5
y
2y 1
lg 5 y 2 y 1
1
1;
;
2
2
3 lg 4 y 5 y 1 3 lg 4 y 5 y 1
2
lg 4 y 2 5 y 1
lg
4 у 5 у 1
2
5 y
2
5 y
2
2y 1 1
2 y 1 log 4 y 2 5 y 1 4 y 5 y 1 0
2
24.
log a ( x ) f ( x) log a ( x ) g ( x) 0,lg
4 у 5 у 1
2
5 y
2
2 y 1 log 4 y 2 5 y 1 4 y 5 y 1 0
2
4 y 2 5 y 1 0,
2
4 y 5 y 1 1,
2
5 y 2 y 1 0,
4 y 2 5 y 1 1 5 y 2 2 y 1 4 y 2 5 y 1 0;
Ответ:
1
5
3,0) 0; 1; .
4
4
25.
9x 1
).
2
2
log 2,1 x 10 log 1,9 x 9 log 2,1 x 10 log 1,9 x.
log3 x 1
x
ОДЗ: x 1 0,
x
x 0,
x 10 0, x
x
x 10 2 1;
x
При: х >1 log 1, 9 x 0.
1,
x
0,
x
10,
x
11,
x
9
1,
10,
11,
9.
Делим обе части неравенства на log 1,9 x
26.
9x 1
;
2
2
log 2,1 x 10
9 log 2,1 x 10
log3 x 1
x 1
2
9 log 2 ,1 x 10
log3 x 1
81
log 3 3 log 3 x 1
2
2,1 1 x 10 1
4
0;
log3 x 1
0;
4 log 3 x 1 log 3 x 1
0;
2
x 10 1
27.
4 log x 10;
2
х 20 х 99
2
3
2 log 3 x 1 2 log 3 x 1
0.
x 9 x 11
Так как log 3 9 log 3 x 1 log 3 9 log 3 x 1 ,
1
3 1 9 x 1 3 1 9 x 1
x 9 x 11
1
0;
28.
14 10 x 9
x 1
0;
x 9 x 11
10 x 9 x 10 0.
x 9 x 11 x 1
Ответ:
10
;9 10;11 .
9
29.
.25 х 30 5 х 125 0,
8).
log х ( х 1) log х ( х 1) 0.
5 t (t 0)
t2-30t+125 0 , (t-5)(t-25) 0 0 t 5,
t 25
х
0 5 5,
х 1,
1).25 30 5 125 0.
х
х
5 25;
х
х
х 2.
2). log x ( x 1) log x ( x 1) 0.
30.
2). log x ( x 1) log x ( x 1) 0.х 0,
х 1,
х 1,
х 1,
( х 1)( х 2)( х 1) х 0
х 1;2.
. Общим решением совокупности
х 1,
х 1,
х 2 и системы х 2 есть число 2.
Ответ: 2.
31.
9).Ответ:(0;0,5) U [2;3]
32.
10).Ответ:
33.
11). log 32 x 2 7 x 6
x
0
3
lg x lg 3
1
2
(lg( 2 x 7 x 6) lg 1)
3
0
34.
x 30
(2 x 2 7 x 6) 1
x 0
2 x 2 7 x 6 0
x 3
( x 2,5)( x 1) 0
x 0
( x 1,5)( x 2) 0
1 x 1,5
2 x 2,5
x 3
Ответ : 1;1,5 2;2,5 3;
35.
Дополнительная формула36.
Метод рационализации впоказательных
неравенствах
37.
(x2-x-2)2x-6 ≥ (x2-x-2)3-4xx2-x-2›0
x2-x-2 ≠1
((x2-x-2)-1)((2x-6)-(3-4x))≥ 0
x›2
x‹-1
, x3=1,5
,x2=
(x2-x-3)(6x-9)≥0
Так как 3‹ √13 ‹4,то
С учётом ОДЗ получаем:
x2 x3 x1
(
; -1) (
U
; +∞)
38.
Ответ:39.
Дополнительная формула40.
Дополнительные формулы41.
42.
43.
В презентации использовались ресурсы:Математика. Подготовка к ЕГЭ-2014: решаем задание С3 методом
рационализации : учебно-методическое пособие/ Под ред. Ф. Ф.
Лысенко,
С. Ю. Кулабухова. - Ростов-на-Дону: Легион, 2013. - 32 с. - (Готовимся
к ЕГЭ.)












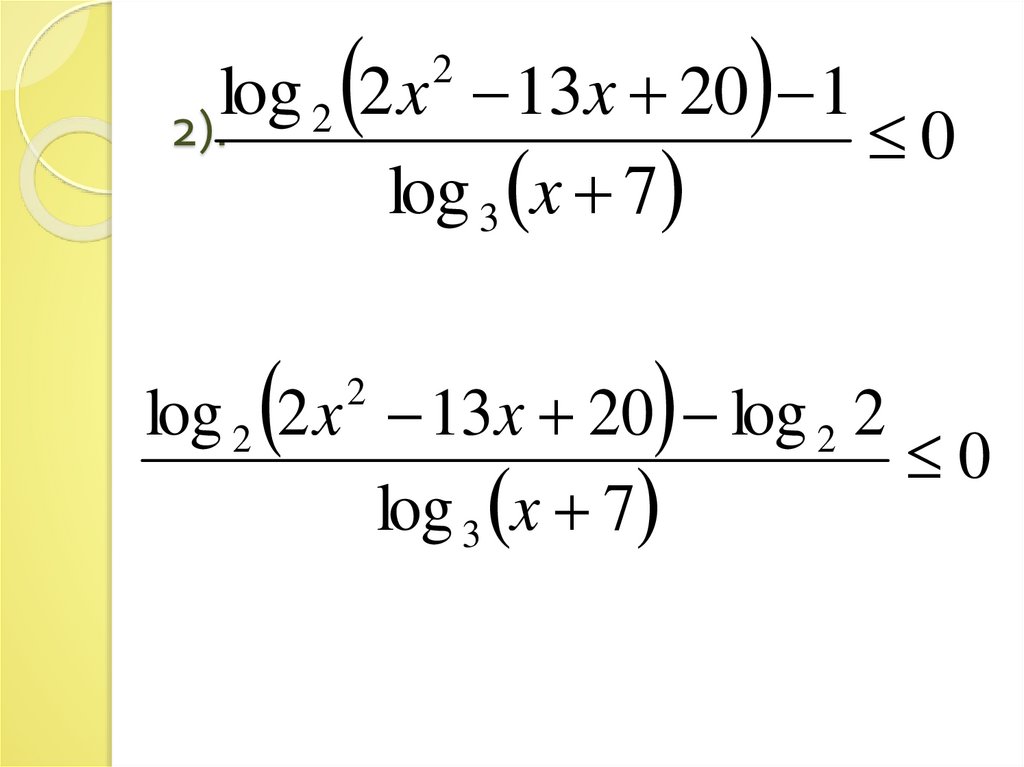
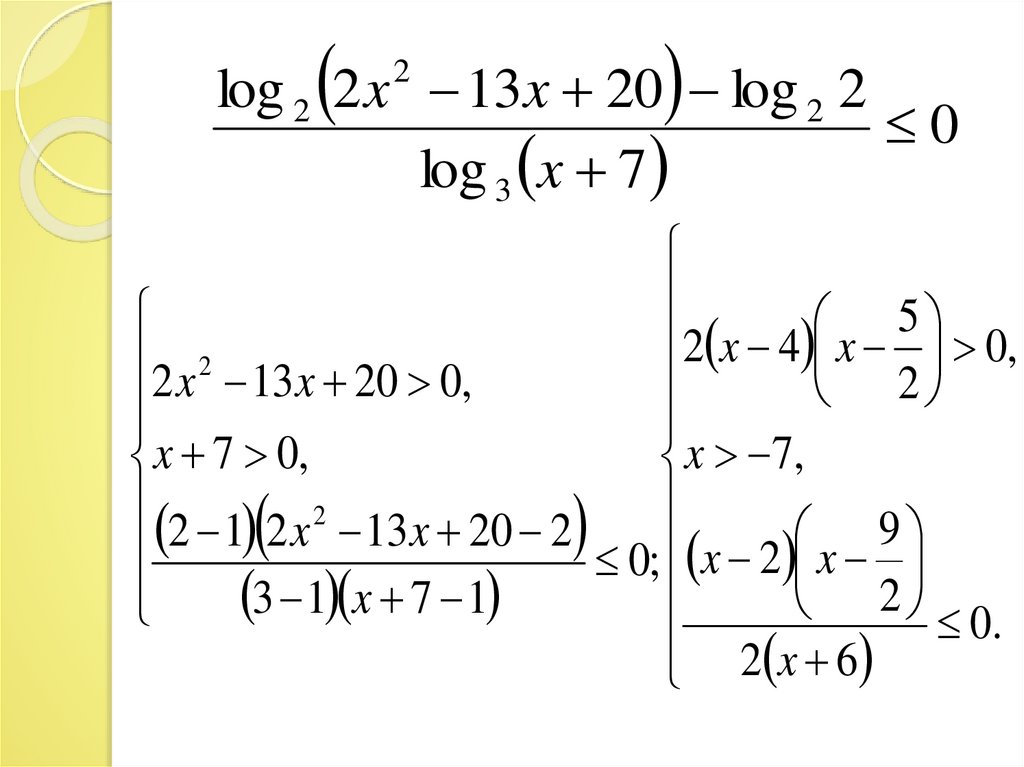


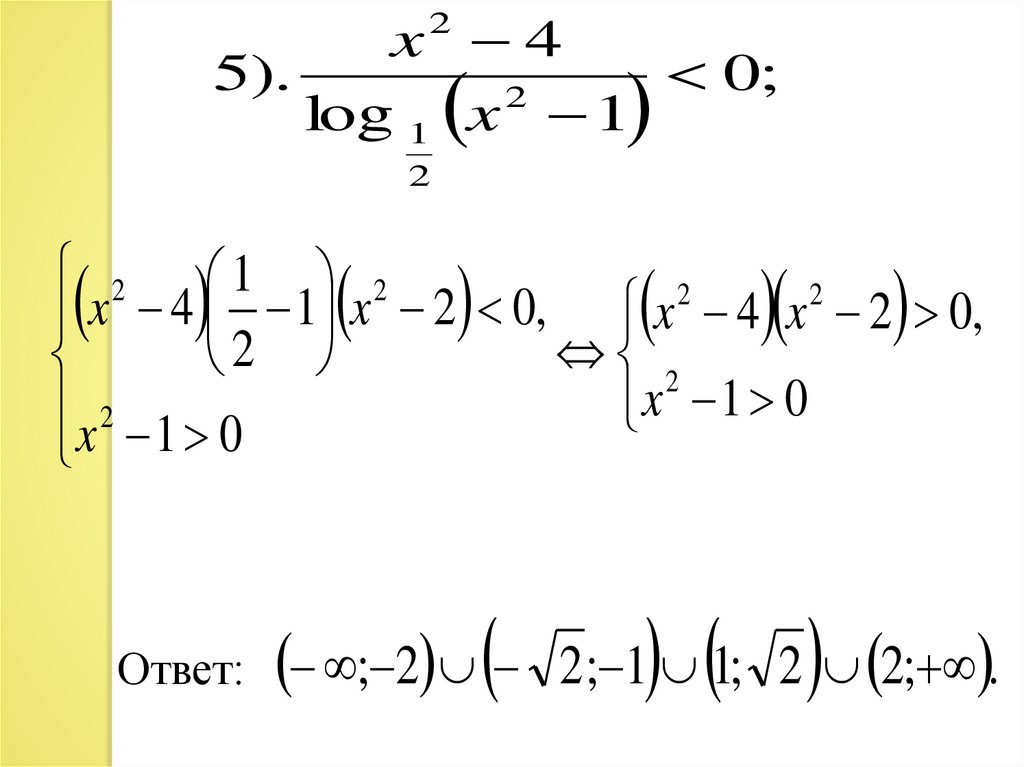



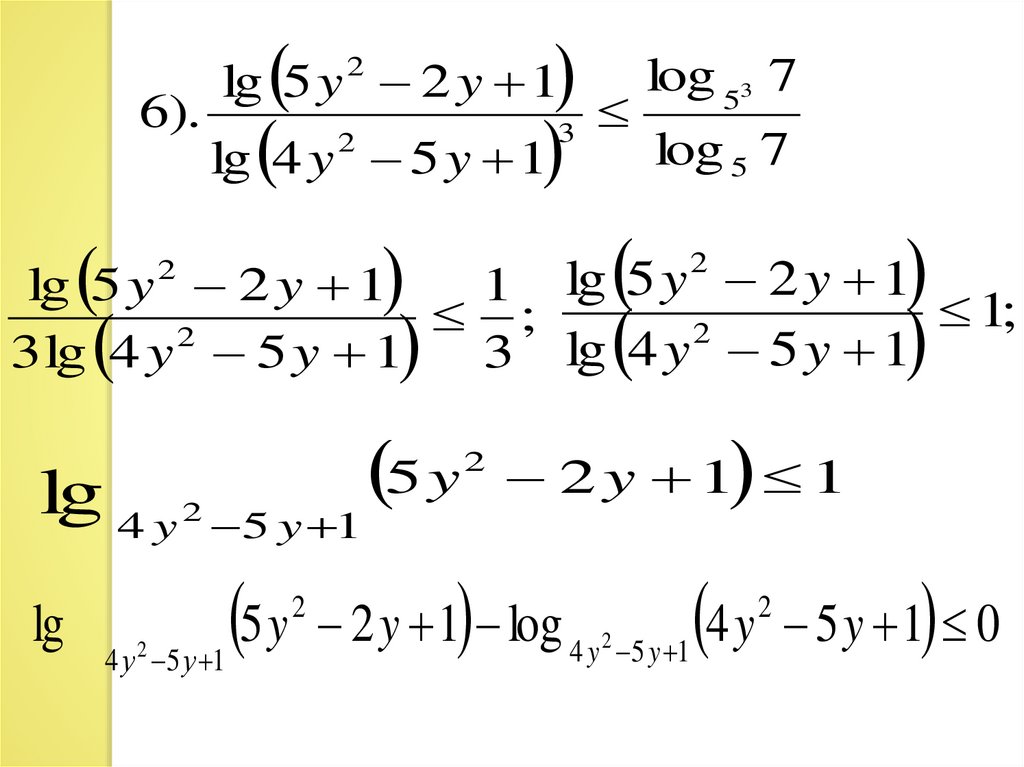


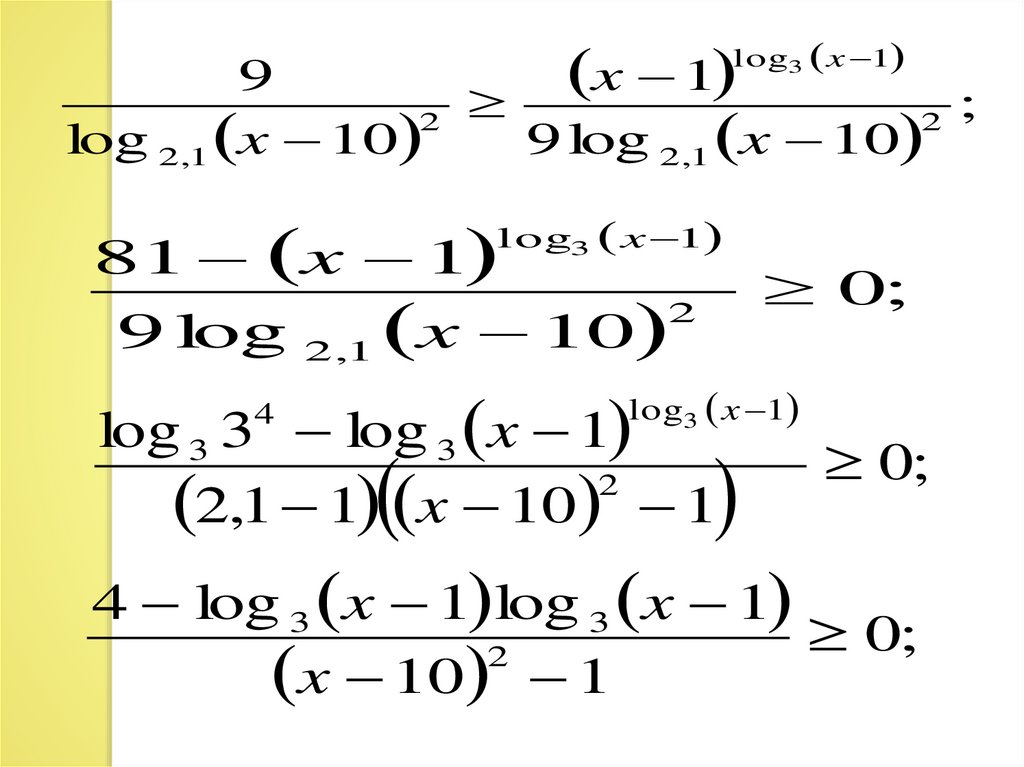

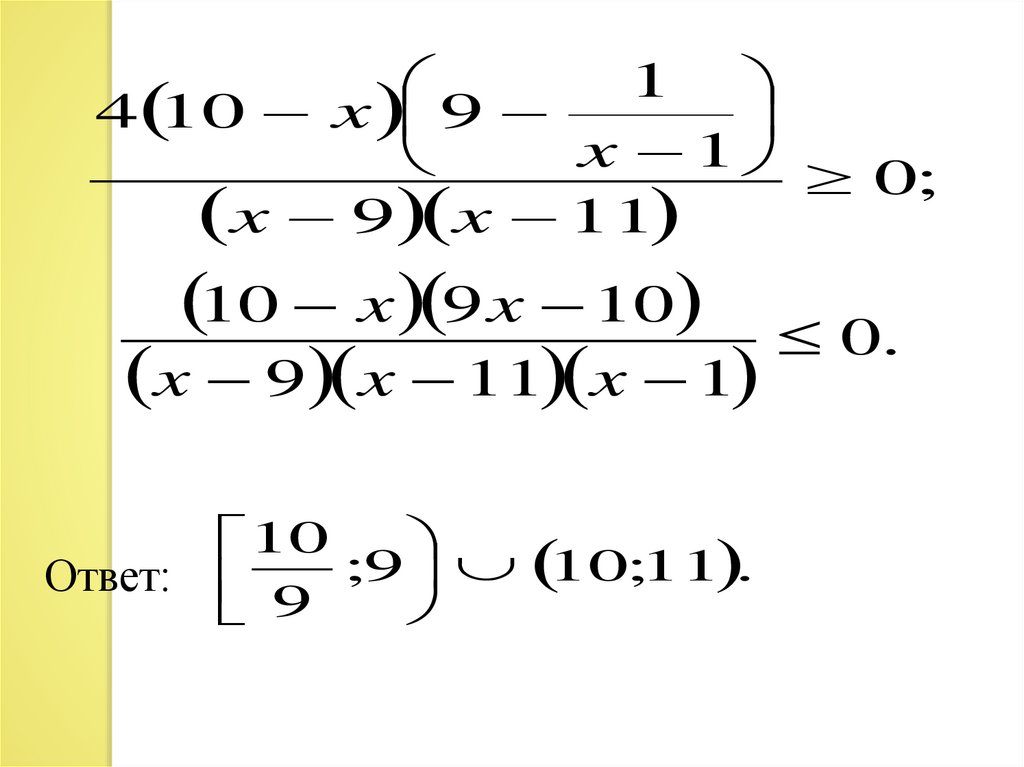
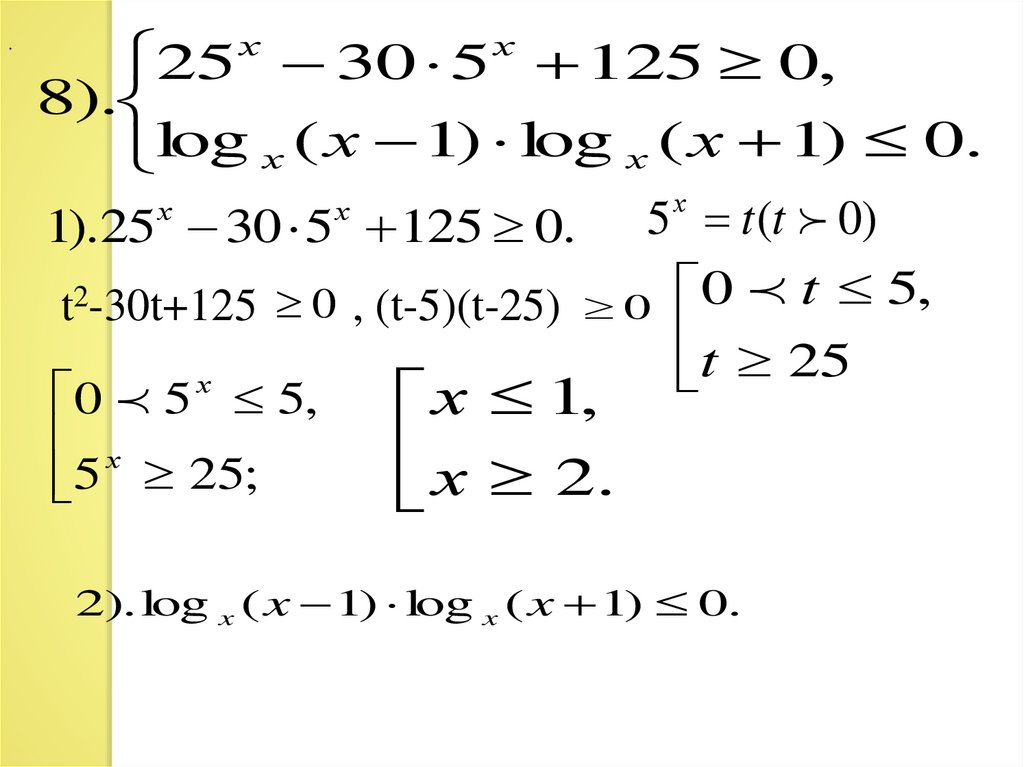



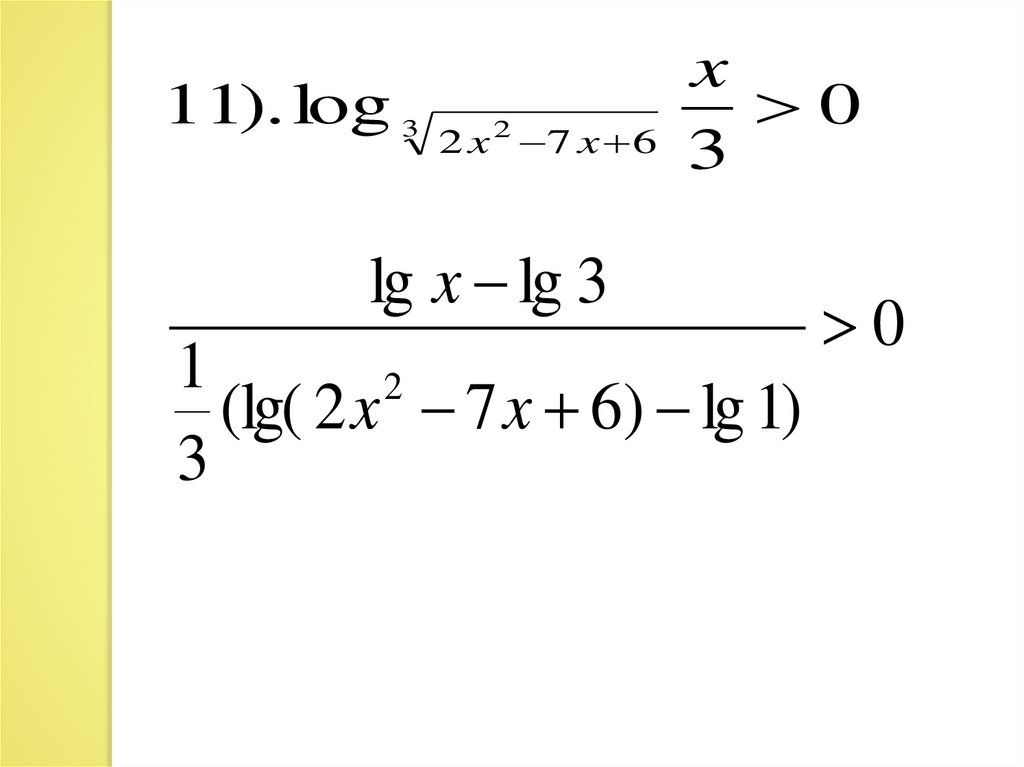



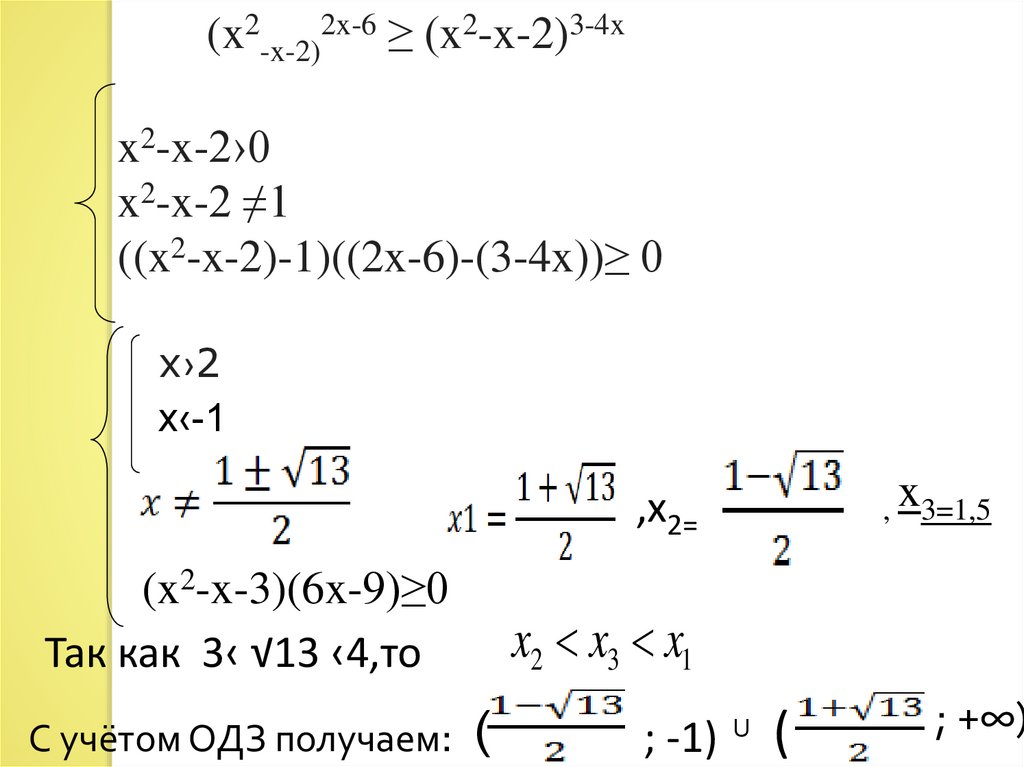



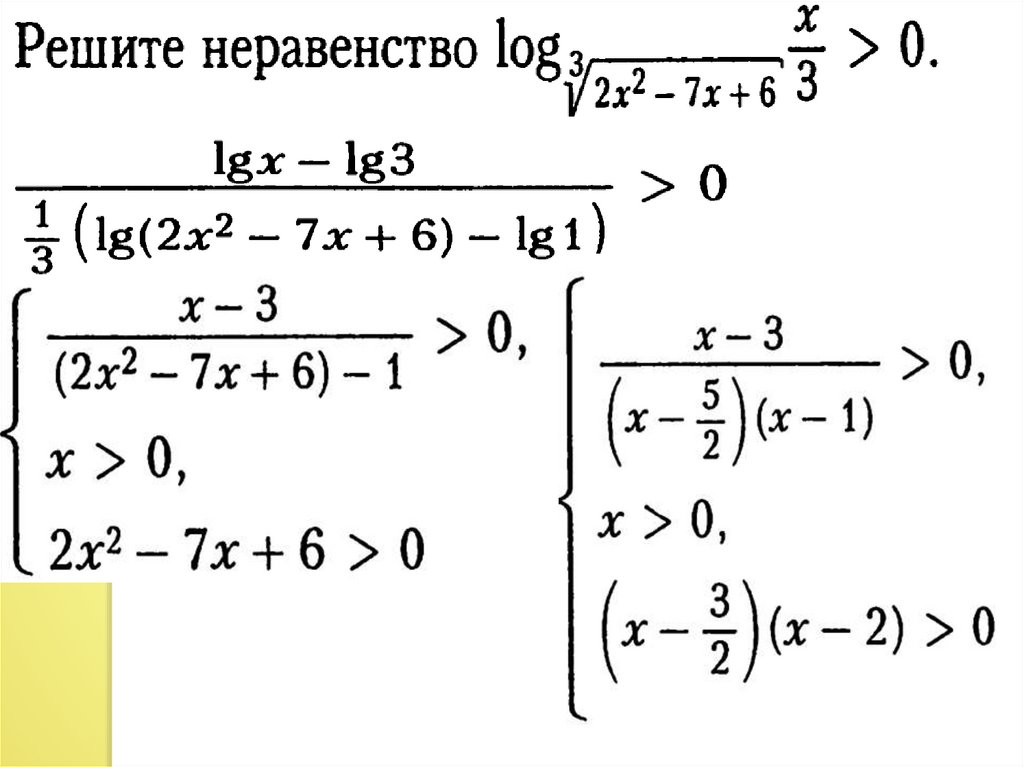

 mathematics
mathematics








