Similar presentations:
Решение неравенств. Задание № 15 на ЕГЭ по математике
1.
2.
«Метод решения хорош,Если с самого начала
мы можем предвидеть –
И впоследствии подтвердить,
Что, следуя этому методу,
Мы достигнем цели.»
Лейбниц
.
3.
Решить неравенство: x log5 3 x x 2 0.Решение:
1)Определим ОДЗ:
3+х−х² >0,
х²-х-3<0,
f(x)= х²-х-3,
х²-х-3=0,
х1
х2
1
13
2
1
13
2
,
.
1 13
1 13
x
2
2
3 13 4
4 13 3
4 1 13 5
3 1 13 2
2
1 13
2 ,5
2
1 ,5
1 13
1
2
2)Упрощаем неравенство, используя метод рационализации, в
котором logn f n 1 f 1
х(5-1)(3+х−х²−1)≥0,
4х(-х²+х+2)≥0 ·(-0,25)
х(х²−х−2)≤0
х(х-2)(х+1) ≤0,
4.
f(x)= х(х-2)(х+1),х(х-2)(х+1)=0,
x=0 или х=2 или х=-1
ııııııııııııııııııı
1
хЄ(-∞;-1]
ııııııııııııııııııı
0
[0;2]
2
х
Пересечение с ОДЗ дает решение
ııııııııııııııııııı
1
ııııııııııııııııııı
0
2
ııııııııııııııııııııııııııııııııııııııııııııııııııııı
1 13
1 13
2
2
1 13
х
; 1 0 ;2
2
1 13
Ответ :
; 1 0 ;2
2
х
х
5.
СамостоятельноРешить неравенство:
2
5
x
13
log
x
6 x 10 0
2 x 5
Решение:
x 2 ,5 ,
2 x 5 ,
x 2 ,5 ,
2 x 6 ,
x 3,
2 x 5 1,
x 3.
2
2
2
x 6 x 10 0 x 6 x 9 1 0 x 3 1 0
2).Применим метод рационализации.
1).Найдем ОДЗ: 2 х 5 0 ,
(5х-13)(2х-5-1)(х²-6х+10-1)≥0;
(5х-13)(2х-6)(х-3)² ≥0;
2·(5х-13)(х-3)(х-3)² ≥0;
(5х-13)(х-3)³ ≥0;
Получаем следующие точки на числовой оси: х=2,6 и х=3
ııııııııııııııııııııı
2,6
х 2 ,6
х 3
ıııııııııııııııııııı
3
х
6.
Пересечение с ОДЗ дает решениеıııııııııııııııııııı
2,6
ıııııııııııııııııııı
х
3
ıııııııııııııııııııııııııııııııııııııııııııııııııı
х
3
2,5
2 ,5 x 2 ,6
x 3
Ответ:(2,5;2,6] (3;+∞).
7.
Решите неравенство log2 x x 2 log x 3 3 x 0Решение.
ОДЗ:
2 x 0 , х 2 ,
2 x 1, x 1,
x 2 0 , x 2 ,
x 3 0 , x 3 ,
x 3 1 , x 2 ,
3 x 0 ; x 3
-3
-2
1
2
x 2; 1 1; 2 .
log2 x x 2 log x 3 3 x 0
(2−х−1)(х+2 − 1)(х+3 −1)(3 −х −1)≤0,
(1−х)(х+1)(х+2)(2 −х)≤0,
(х−1)(х+1)(х+2)(х −2)≤0,
Получаем следующие точки на числовой оси:
+
−
ııııııııııııı
-2
-1
+
−
ııııııııııııı
1
x 2 ; 1 1;2
2
+
х
х 2 ,
х 1 ,
х 1,
х 2
3
x
8.
C учетом ОДЗ , имеемııııııııııııı
ııııııııııııı
2
х
ıııııııııııııııııııııııııııııııııııııııııııı
х
-2
-2
-1
1
1
x 2; 1 1; 2 .
Ответ : 2 ; 1 1; 2 .
2
9.
Решить неравенство:Решение.
log3 9 x log4 64 x
0.
2
5x x
x 0
x 0,
x
0
,
2
2
1
5 x x 0 ; 5 x x 0 ; x 5 x 1 0 ; x 5 .
Найдем ОДЗ: x 0 ,
хЄ(0;0,2)U(0,2;+∞)
Воспользуемся методом рационализации, в котором
loga f 0
a 0 ,a 0
a 1 f 1 0
при х>0
х х,
f 0
log3 9 x log4 64 x
0;
5 х2 х
log3 9 x log4 64 x
0;
х 5 х 1
3 1 9 x 1 4 1 64 x 1 0 ;
х( 5 x 1 )
6 9 x 1 64 x 1
1
0 ;
х( 5 x 1 )
6
имеем:
9 x 1 64 x 1 0 ;
х( 5 x 1 )
10.
11
1
1
9 x x 64
x
x
5
9
64
9
64
Получим:
0
0;
1
1
9 64
5 x x
x x
5
5
Получаем следующие точки на числовой оси:
х
х
х
х
1
0
x
64
1 x 1
5
9
ııııııııııııııııı
0
0
1
64
1
9
1
5
1
64
ııııııııııııııııı
1
9
Пересечение с ОДЗ дает решение
1 1
х 0 ; ;0 ,2 .
64 9
1 1
Ответ : 0 ; ;0 ,2 .
64 9
1
5
х
11.
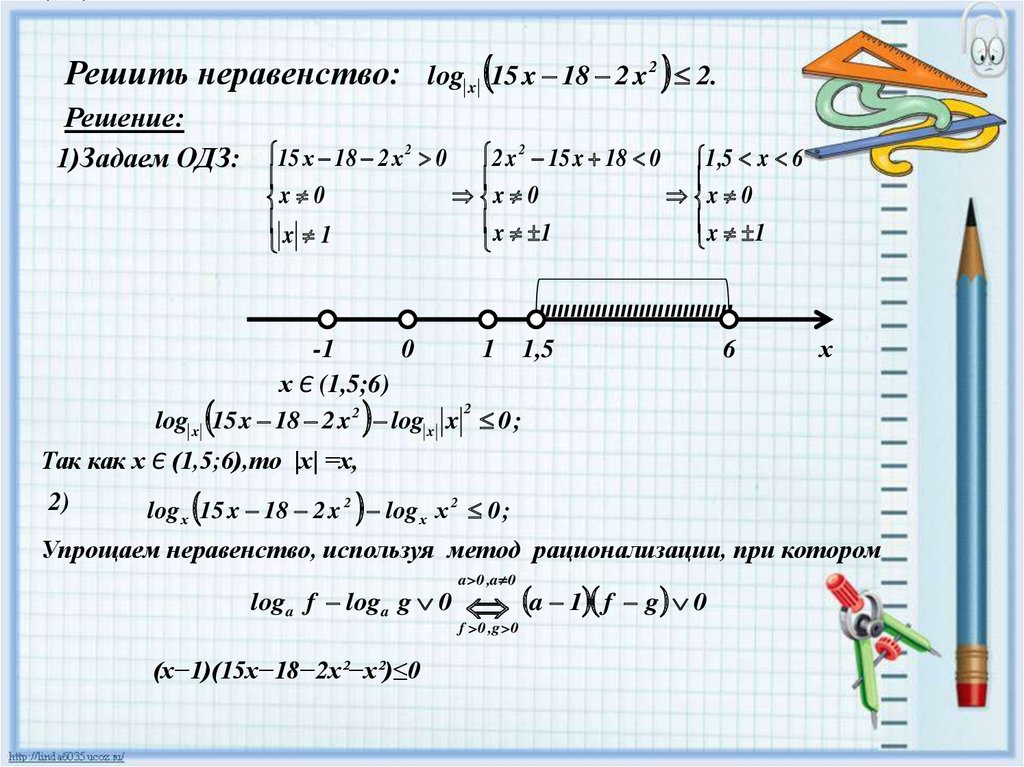
Решить неравенство: log x 15 x 18 2 x 2 2.Решение:
1)Задаем ОДЗ: 15 х 18 2 х 2 0
x 0
x 1
2 x 2 15 x 18 0 1 ,5 x 6
x 0
x 0
x 1
x 1
ııııııııııııııııııııııııııııııı
-1
0
1 1,5
х Є (1,5;6)
2
log x 15 x 18 2 x 2 log x x 0 ;
6
х
Так как х Є (1,5;6),то |х| =х,
2)
log х 15 x 18 2 x 2 log х х 2 0 ;
Упрощаем неравенство, используя метод рационализации, при котором
loga f loga g 0
(х−1)(15х−18−2х²−х²)≤0
a 0 ,a 0
a 1 f g 0
f 0 ,g 0
12.
(х−1)(15х−18−3х²)≤ 01
· 3
(х-1)(х²-5х+6)≥0,
(х-1)(х-2)(х-3)≥0.
Получаем точки, делящие числовую ось:
х 1,
х 2,
х 3
1
2
3
х
Пересечение с ОДЗ дает решение данного неравенства
ııııııııııııııııııııı
1
2
ıııııııııııııııı
3
ııııııııııııııııııııııııııııııııııııııı
1,5
6
x Є(1,5;2] [3;6);
Ответ: (1,5;2]
[3;6).
х
х
13.
Решить неравенство:log52 25 x 2 3 log5 25 x 2 2 0.
Решение:
1) .Найдем ОДЗ: 25 x 2 0 ;
x 2 25 0 ;
x 5 x 5 0 ;
ııııııııııııııııııııııııııııııı
х
-5
5
хЄ(-5;5)
log5 25 x 2 t , получим t 2 3 t 2 0
2).Делаем замену
t 2 3t 2 0
t 1 1; t 2 2
t 1 t 2 0
ıııııııııııııııı
1
ıııııııııııııııı
2
t
14.
Переходя к х, имеем:2
2
t 1 log5 25 x 1 log5 25 x log5 5
t 2
2
2
log5 25 x 2 log5 25 x log5 25
5 1 25 х 2 5 0
х 2 20 0
2
2
5 1 25 х 25 0
х 0
Пересечение с ОДЗ дает решение
ııııııııııııııııııııııııııııııııııııııı
ıııııııııııııııııııııııııııııııııııııı
2 5
0
х
2 5
ıııııııııııııııııııııııııııııııııııııııııııııııııııııııııııııııı
5
5
х ( 5 ; 2 5 ] { 0 } [ 2 5 ;5 ).
Ответ:
х 2 5 х 2 5 0
х 0
( 5 ; 2 5 ] { 0 } [ 2 5 ;5 ).
х
15.
Решить неравенство:5
x
125 log x 1 x log x 1 3
x 2x
2
x 10
2
x 8 x
0.
Решение:
5
x
5 3 log x 1 x log x 1 3
x 2x
2
x 10 x 8 x
2
0.
Упрощаем неравенство, используя метод рационализации
x 0,
x 1 0,
x 1 1,
x 3 x 1 1 x 3
0
2
2
2
2
x 2 x x 10 x 8 x
x 1;
x 2;
2
x 2
x
3
0;
x 2 2 x x 2 10 x 8 x x 8 x
х 1;
x 2;
2
x 2 0 ;
x
3
2 8 x 5 x 4
16.
х 1;x 2;
x 3 2 x 2 0 ;
x 5 x 4
ııııııııııııııııııııııııııııııııııııııııııııııııııııııııııııııııııııııııııııııııı
1
2
ıııııııııııııııııııııııı
2
!
3
ııııııııııııııııı
5
4
1 x 2
x 3
4 x 5
Ответ:(1;2) {3} (4;5).
х
х
17.
Решить неравенство: log logx 2 x 5 x 2 0.Решение:
1)Найдем ОДЗ
2
х
,
5
5 x 2 0 ,
x 0,
x 0 ,4 ,
0 ,4 x 0 ,5
log
2
x
0
,
x
1
,
x
1
,
x
x 1
log 2 x 1
x 1 2 x 1 0 ,
x 1
x
x 1 2x x 0
x 0 ,5
2)
log x 2 x 1 5 x 2 1 0 ,
x 1 2 x x 5 x 3 0 ,
x x 1 5 x 3 0 ,
f x x x 1 5 x 3 ,
x 1 0 , x 2 1 , x 3 0 ,6
0
0,6
1
х
18.
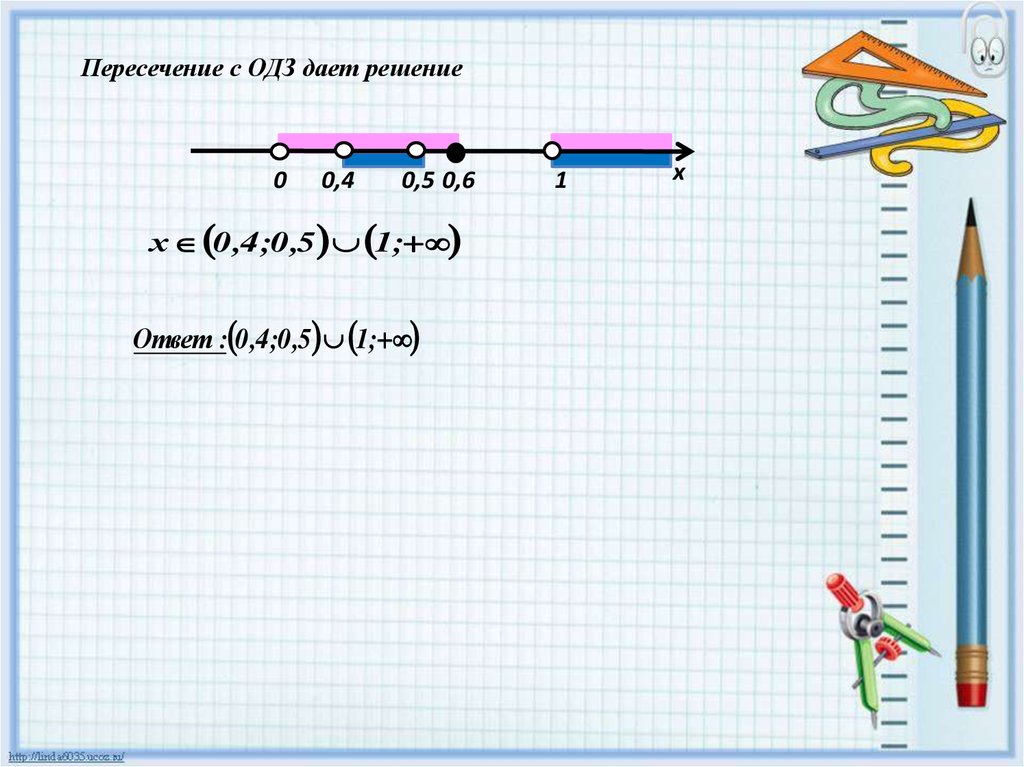
Пересечение с ОДЗ дает решение0
0,4
0,5 0,6
х 0 ,4 ;0 ,5 1;
Ответ : 0 ,4 ;0 ,5 1;
1
х
19.
Решить неравенство:log 3 x 1 2 x 2 x 1 log 3 x 1 11 x 6 3 x 2 ,
x 2
x 2
Решение.
1)Найдем ОДЗ:
2 х 2 х 1 0 ,
2
11 x 6 3 x 0 ,
3x 1
0,
x 2
3x 1
1.
x 2
Решим по отдельности каждое неравенство
a)2x²+x-1>0,
f(x)=2x²+x-1,
2x²+x-1=0
х 1 1 , х 2 0 ,5
х 0 ,5
x 1
б)11x-6-3x²>0,
f(x)=11x-6-3x²,
11x-6-3x²=0,
х 1 1 , х 2
1
х
3
x 1
1
3
20.
в)3x 1
0 3 х 1 х 2 0 ,
x 2
f x 3 х 1 х 2 ,
3 х 1 х 2 0 ,
1
; x 2 2
3
1
x
3
x 2
x1
-2
-1
1
3
г) 3 x 1
1,
x 2
3х 1 х 2,
2 х 3,
х 1 ,5
0,5
2
3
1,5
3
х
2
х ;1 ,5 1 ,5 ;3 .
3
4)Возвращаемся к исходному неравенству и воспользуемся
методом рационализации: log f log g n 1 f g
n
n
На заданном ОДЗ можем записать
3х 1
1 2 х 2 х 1 11 х 6 3 х 2 0 ,
х 2
21.
3х 11 2 х 2 х 1 11 х 6 3 х 2 0 ,
х 2
3х 1 х 2
5 х 2 10 х 5 0 ,
х 2
2х 3
1
5 х 2 10 х 5 0
х 2
5
2х 3 2
х 2х 1 0,
х 2
2х 3
х 1 2 0 ,
х 2
Получаем следующие точки на числовой оси:
-2
1
х
1,5
х ; 2 1 1,5 ;
х 2 ,
х 1 ,5 ,
х 1
Пересечение с ОДЗ дает решение:
-2
х 1 1,5 ;3 .
Ответ : 1 1,5 ;3 .
2
3
1
1,5
3
х
22.
Используемые материалы1.ЕГЭ 2018. Математика. Профильный уровень.
Под ред. И.В. Ященко.− 36вариантов. Издательство
«Национальное образование»
2.http://mathege.ru/or/ege/Main.html − Материалы
открытого банка заданий по математике
источник шаблона:
Фокина Лидия Петровна
учитель начальных классов
МКОУ «СОШ ст. Евсино»
Искитимского района
Новосибирской области
СПАСИБО АВТОРАМ ФОНОВ И КАРТИНОК




















 mathematics
mathematics