Similar presentations:
Общие методы решения уравнений
1.
Общие методырешения уравнений
2. Цели урока:
Рассмотреть общие методырешения уравнений.
Научиться применять эти методы
при решении уравнений.
Формировать навыки применение
наиболее рациональных способов
решения уравнений.
3. Рассмотрим уравнения:
1) х² - 2 х = 0;2) sin²x + sinx = 0;
3) 7
49;
2
4) log 2 x 4 log 2 x 3 0;
х 5 х
2
5)
1
х
х
4.
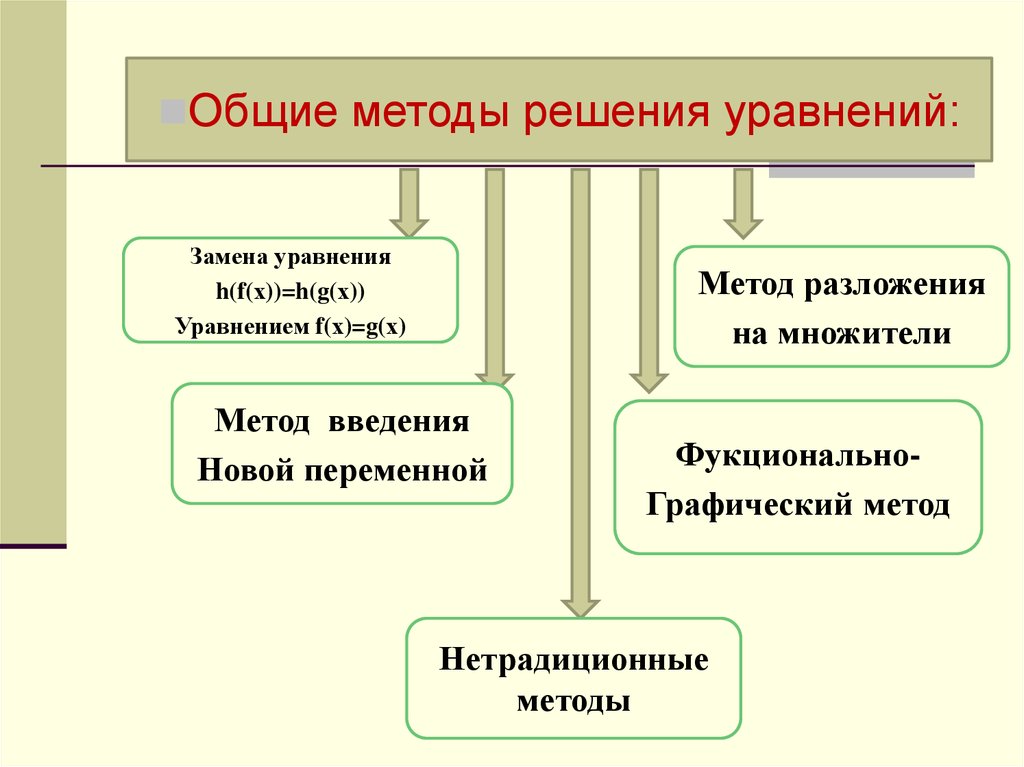
Общие методы решения уравнений:Замена уравнения
h(f(х))=h(g(х))
Уравнением f(х)=g(х)
Метод разложения
на множители
Метод введения
Новой переменной
ФукциональноГрафический метод
Нетрадиционные
методы
5. Замена уравнения более простым уравнением
Суть метода: от уравнения видаh(f(х))=h(g(х))
осуществить переход к уравнению вида
f(х)=g(х)
6. Метод применяется:
При решении показательных уравнений:a
f x
a
g x
a 1; а 0
f(x)=g(x)
При решении логарифмических уравнений:
log a f x log a g x
a 1; а 0
f(x)=g(x)
f x 0
g x 0
При решении иррациональных уравнений:
f(x)=g(x)
7. Метод применяется: Метод нельзя использовать:
Метод применяется:если функция монотонная
f(x)2 k 1 g(x)2 k 1
f(x)=g(x)
Метод нельзя использовать:
если функция
периодическая
Например,
sin (3x-1) = sin (3x+4)
Например:
(2x+3)3=(5x-9)3
2x+3=5x-9
x=4
Ответ: 4
если функция четная
Например,
(2x+7)2 = (5x -12)2
8. Пример 1:
Решить уравнение2 х 3 х 1
5
5 0
2 х 3 х 1
5
5;
2
2
2 х 3х 1 1;
2
2 х 3х 0;
х 0; х 1,5.
2
Ответ: 0; 1,5.
9. Пример 2:
log 3 x 3x 5 log 3 7 2 x ;2
х 3х 5 7 2 х;
2
х х 12 0;
х1 4, х2 3.
2
Проверка :
х 2 3х 5 0,
7 2 х 0.
х 4 посторонний
Ответ : 3.
корень
10.
2. Метод разложения намножители.
Уравнение f(x)g(x)h(x) = 0 можно заменить
совокупностью уравнений:
f ( x ) 0;
g ( x ) 0;
h( x ) 0.
Решив уравнения этой совокупности, нужно
взять те их корни, которые принадлежат
ОДЗ исходного уравнения, а остальные
отбросить как посторонние.
11. Пример 3:
Решить уравнениех 2 3 2
х 6 х 5
2
х 2 3 0;
х 2 6 х 5
1;
2
ln(
х
8
)
0
.
1 ln( х 8) 0.
х 2 9;
2
х
6
х
5
0
;
х 8 1.
12. Пример 3:
х1 7;х 1; х 5;
3
2
х 4 9.
Проверка : ОДЗ :
х 2 0,
х 8 0.
Из найденных корней этой системе
неравенств удовлетворяет только
х = 9, остальные являются
посторонними для данного уравнения.
Ответ: 9.
13.
3. Метод введения новойпеременной.
Если уравнение f(x)= 0 удалось
преобразовать к виду p(g(x)) = 0, то нужно
ввести новую переменную u = g(x), решить
уравнение p(u) = 0, а затем решить
совокупность уравнений: g ( x ) u ;
1
g ( x) u ;
2
....
g ( x) un
где и1 , и2 ,… ип - корни уравнения р(и) = 0.
14. Пример 4:
Решить уравнение1
2
7
.
2
2
х 3х 3 х 3х 1 5
Введём новую переменную
Получим:
у х 3х .
1
2
7
.
у 3 у 1 5
2
Освободившись от знаменателей,
получим:
2
7 у 29 у 4 0;
15. Пример 4:
Найдём корни квадратного1
уравнения:
у1 4; у 2
7
.
Выполним проверку корней на
выполнение условия:
5(у – 3)(у + 1) ≠ 0.
Оба корня удовлетворяют данному
условию.
16. Пример 4:
Вернёмся к замене переменной ирешим два уравнения:
х 3х 4
2
х 1 1; 4.
2
Ответ:
1; 4;
и
х3
4
1
х 3х .
7
2
21 469
.
14
21 469
.
14
17. 3. Функционально-графический метод.
Чтобы графически решитьуравнение f(x) = g(x) нужно
построить графики функций
у = f(x) и у = g(x) и найти точки их
пересечения. Корнями уравнения
служат абсциссы этих точек.
18.
1) Решить уравнениех =|x–2|
Пример 5:
1 шаг: построить графики функций у =
х иу=|x–2|
2 шаг: найти абсциссы точек (или точки) пересечения графиков
у х 2
у
х
Ответ: x1 = 1, х2 = 4
19.
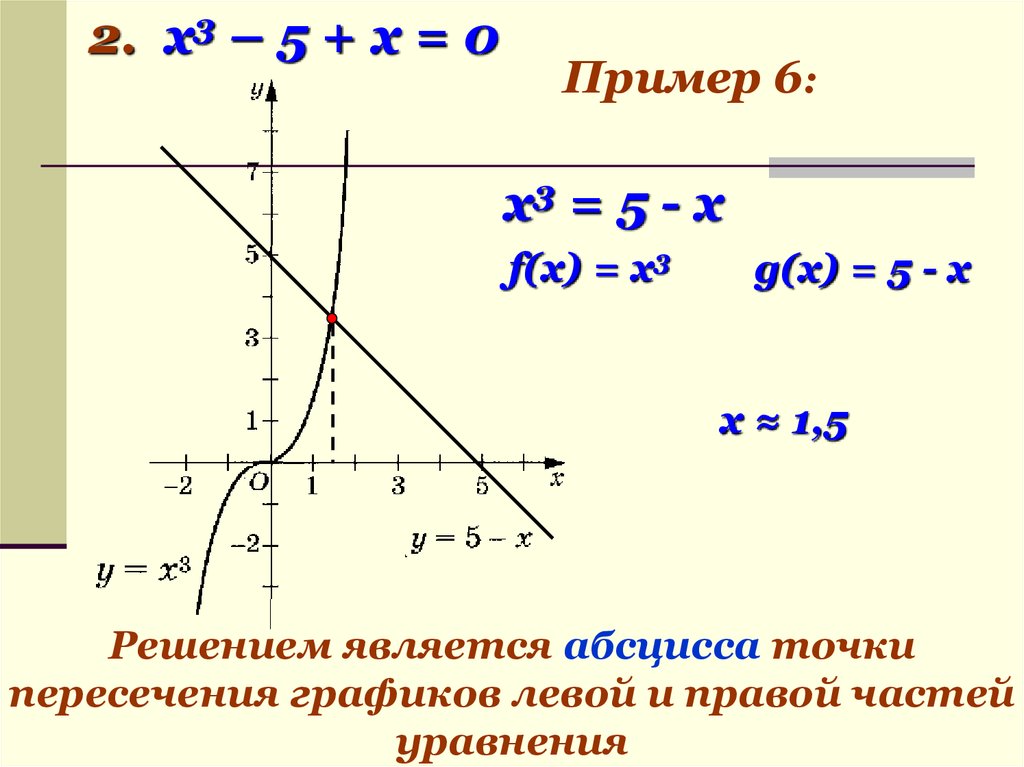
2. x3 – 5 + х = 0Пример 6:
х3 = 5 - х
f(x) = х3
g(x) = 5 - х
х ≈ 1,5
Решением является абсцисса точки
пересечения графиков левой и правой частей
уравнения
20. Пример 7:
Решить уравнениеcos 2 x х 2 х 2.
2
Рассмотрим функцию у = х² - 2х + 2.
Её графиком является парабола,
ветви которой направлены вверх.
В вершине параболы функция
достигает своего наименьшего
значения.
21. Пример 7:
Найдём координаты вершины параболы.b
х0 ; у 0 у ( х0 );
2a
(1;1)
Для функции у = х² - 2х + 2 у наим. 1.
Функция у = cos 2πx обладает
свойством: у
1.
наиб.
22. Пример 7:
Задача сводится к решению системыуравнений
х² - 2х + 2 = 1,
cos 2πx = 1.
Решив 1 уравнение получили: х = 1.
Это значение удовлетворяет и 2
уравнению системы,
следовательно, является
единственным корнем заданного
уравнения.
Ответ: 1.
23.
1. Задание13 № 501689
а) Решите уравнение
б) Найдите все корни этого уравнения, принадлежащие отрезку






























 mathematics
mathematics








