Similar presentations:
Расчет внецентренно сжатых элементов ЖБК. (Тема 11)
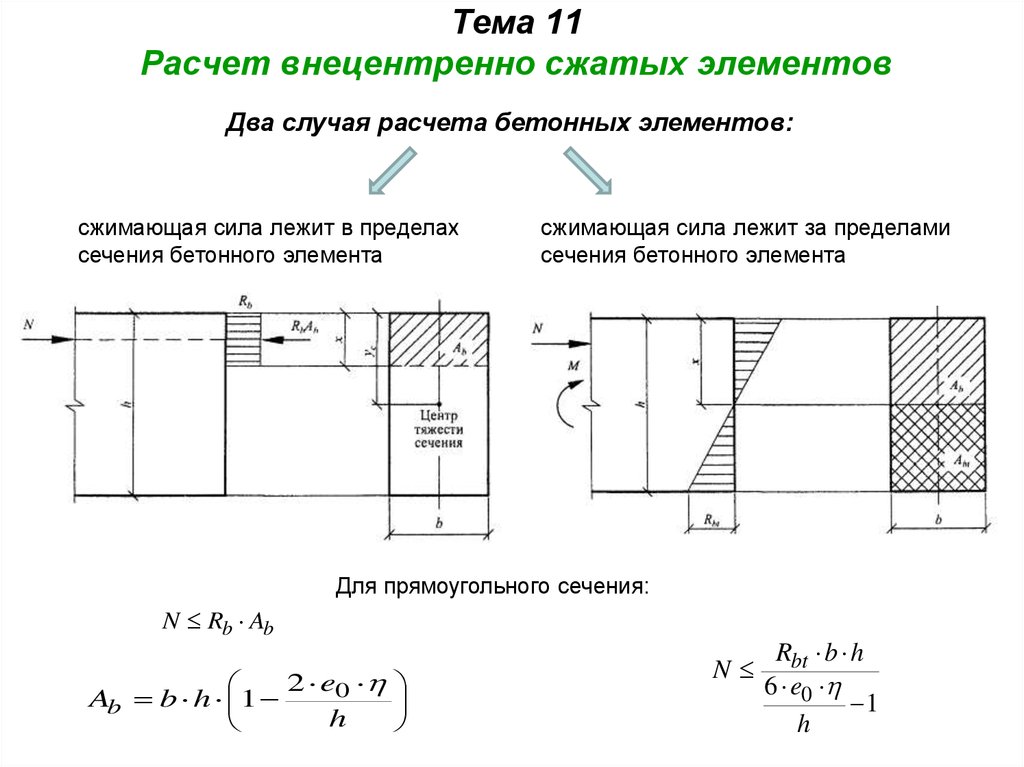
1. Тема 11 Расчет внецентренно сжатых элементов
Два случая расчета бетонных элементов:сжимающая сила лежит в пределах
сечения бетонного элемента
сжимающая сила лежит за пределами
сечения бетонного элемента
Для прямоугольного сечения:
N Rb Ab
2 e0
Ab b h 1
h
N
Rbt b h
6 e0
1
h
2.
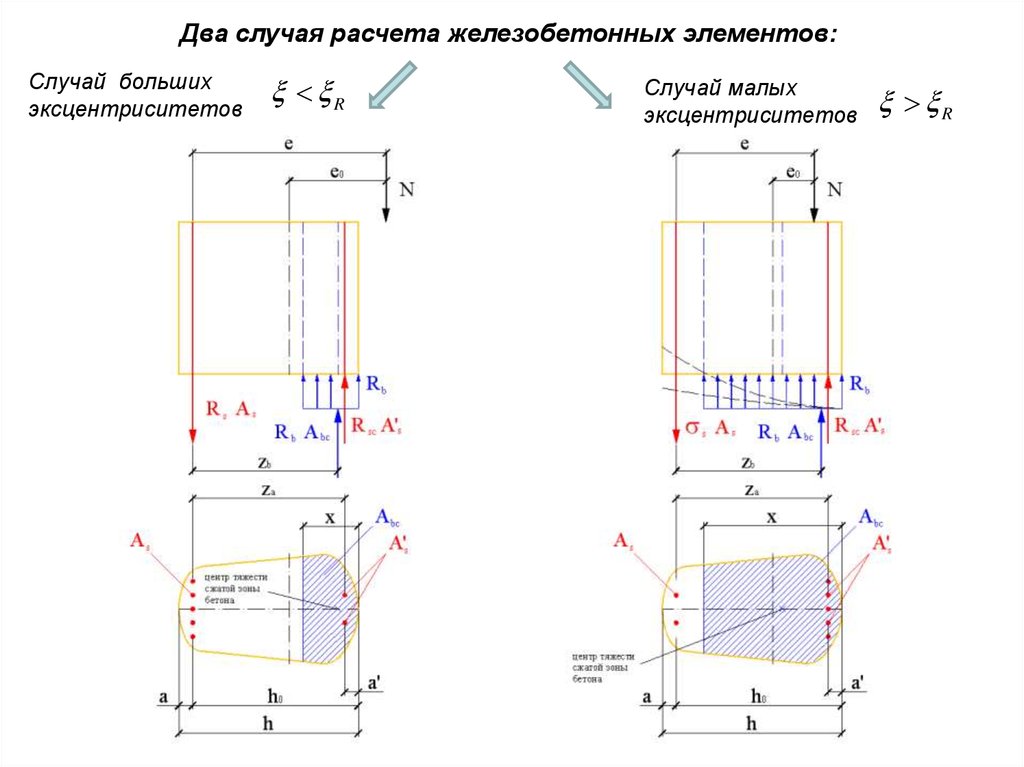
Два случая расчета железобетонных элементов:Случай больших
эксцентриситетов
R
Случай малых
эксцентриситетов
R
3.
Расчет на внецентренное сжатие:В плоскости действия момента:
Для статически
неопределимых конструкций
Для статически определимых
конструкций.
e =max( e0 ; ea)
e = ( e0 + ea)
Из плоскости действия момента:
e = ea
Случайный эксцентриситет ea
Наибольшая из 3-х величин:
• 1/600 длины элемента
Из-за искривления конструкции
1/30 высоты сечения;
Из-за неточности монтажа
Эксцентриситет от внешней нагрузки
10 мм.
Из-за неоднородности структуры.
e0
M
N
4.
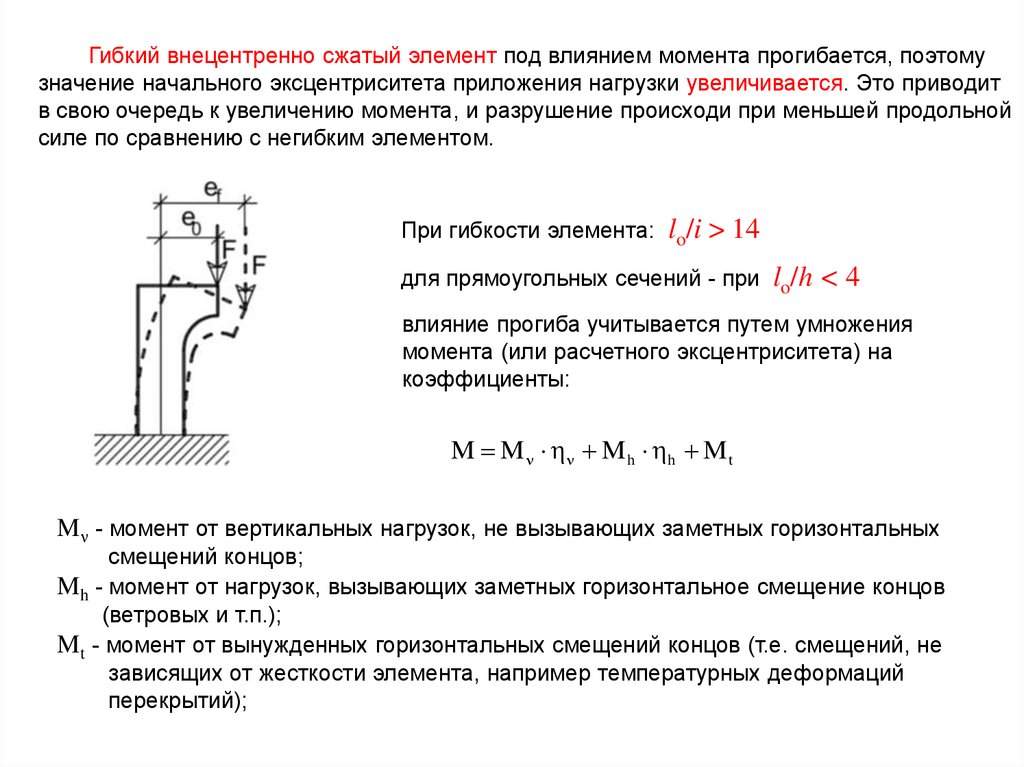
Гибкий внецентренно сжатый элемент под влиянием момента прогибается, поэтомузначение начального эксцентриситета приложения нагрузки увеличивается. Это приводит
в свою очередь к увеличению момента, и разрушение происходи при меньшей продольной
силе по сравнению с негибким элементом.
При гибкости элемента: lo/i >
14
для прямоугольных сечений - при lo/h
<4
влияние прогиба учитывается путем умножения
момента (или расчетного эксцентриситета) на
коэффициенты:
M M M h h M t
M - момент от вертикальных нагрузок, не вызывающих заметных горизонтальных
смещений концов;
Mh - момент от нагрузок, вызывающих заметных горизонтальное смещение концов
(ветровых и т.п.);
Mt - момент от вынужденных горизонтальных смещений концов (т.е. смещений, не
зависящих от жесткости элемента, например температурных деформаций
перекрытий);
5.
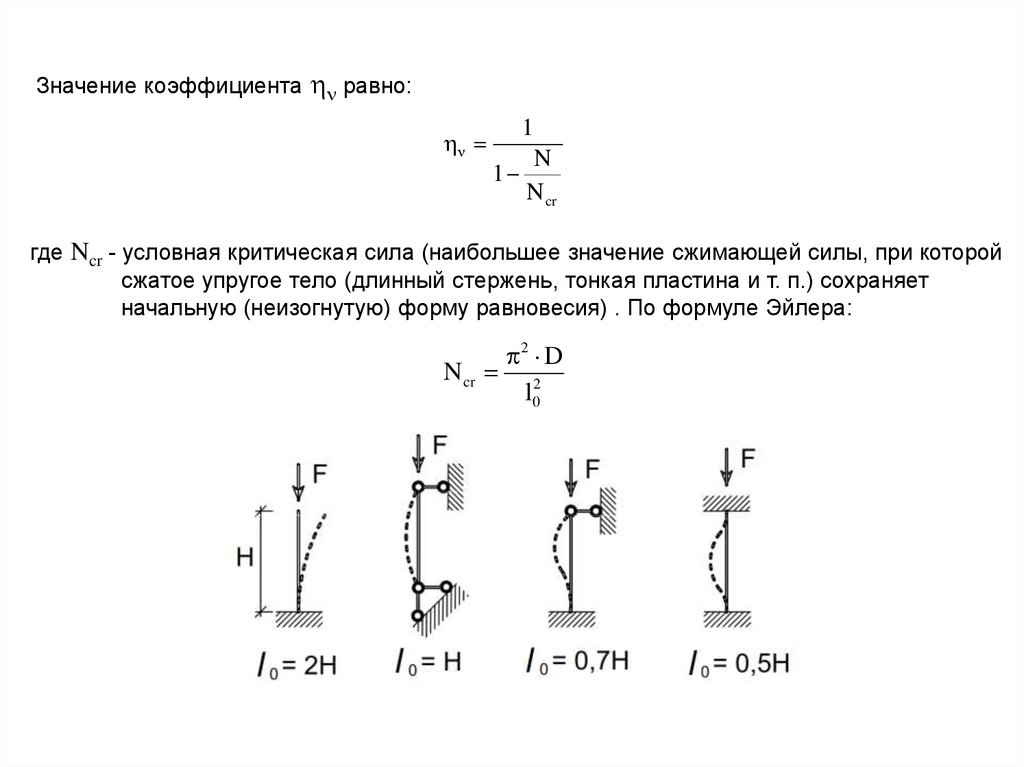
Значение коэффициентаравно:
1
1
N
N cr
где Ncr - условная критическая сила (наибольшее значение сжимающей силы, при которой
сжатое упругое тело (длинный стержень, тонкая пластина и т. п.) сохраняет
начальную (неизогнутую) форму равновесия) . По формуле Эйлера:
2 D
N cr 2
l0
6.
l0 для коэффициента , а также при расчете на действие продольной силы сослучайным эксцентриситетом
Условие опирания
Величина l0
С шарнирным опиранием по концам
1.0 l
Шарнир на одном конце и жесткая заделка на другом конце
0.7 l
Шарнир на одном конце и податливая заделка на другом конце
0.9 l
С жесткой заделкой на двух концах
0.5 l
С податливой заделкой на двух концах
0.8 l
С жесткой заделкой на одном конце и податливой заделкой на
другом
0.7 l
для коэффициента
h
Условие опирания
Величина l0
Шарнир на одном конце и жесткая заделка на другом конце
1.5 l
Шарнир на одном конце и податливая заделка на другом конце
2.0 l
С жесткой заделкой на двух концах
0.8 l
С податливой заделкой на двух концах
1.2 l
С жесткой заделкой на одном конце и податливой заделкой на
другом
1.0 l
7.
D – жесткость железобетонного элемента в предельной стадии.D K b Eb I K s E s I s
Kb и Ks – коэффициенты, определяемые по СНиП
Для произвольного сечения :
D
0.15 E b I
0.7 E s I s
l 0.3 e
Для прямоугольного сечения :
2
0.0125
h
a
'
D Eb b h
0.175 0
l 0.3 e
h
3
I и Is – момент инерции бетонного сечения и сечения всей арматуры относительно центра
тяжести бетонного сечения;
l – коэффициент, учитывающий влияние длительного действия нагрузки на прогиб
элемента;
e – коэффициент, принимаемый равным e0/h но не менее 0.15;
A s A 's E s
b h
Eb
8.
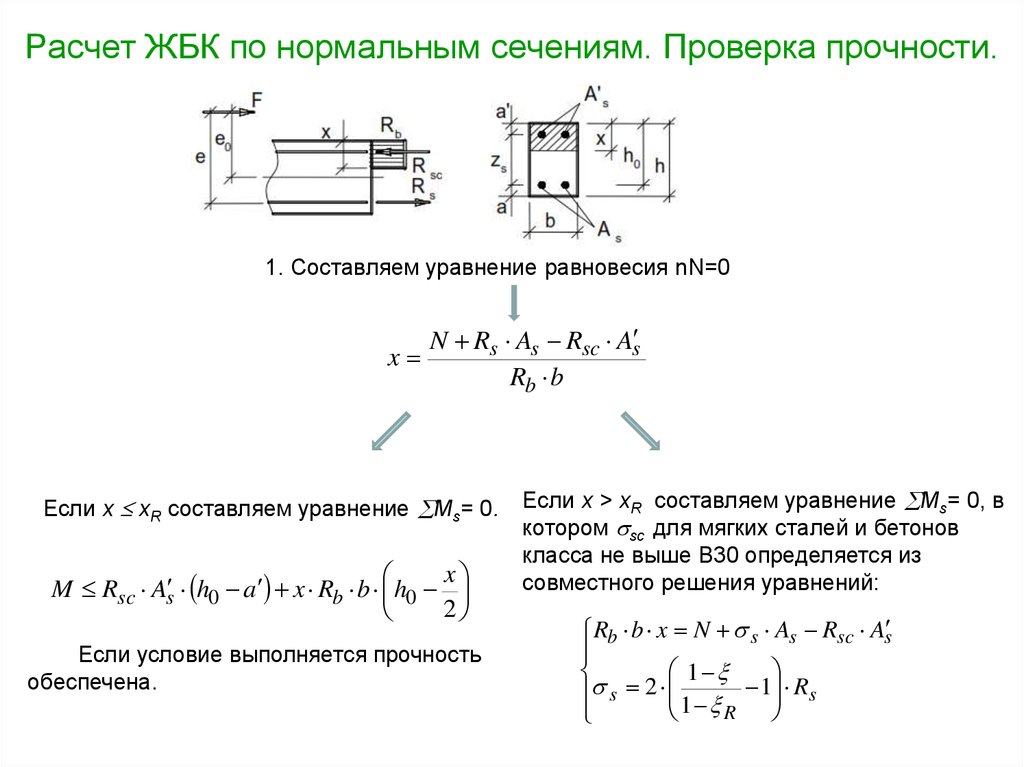
Расчет ЖБК по нормальным сечениям. Проверка прочности.1. Составляем уравнение равновесия nN=0
x
N Rs As Rsc As
Rb b
Если х хR составляем уравнение Ms= 0.
x
M Rsc As h0 a x Rb b h0
2
Если условие выполняется прочность
обеспечена.
Если х > хR составляем уравнение Ms= 0, в
котором sc для мягких сталей и бетонов
класса не выше В30 определяется из
совместного решения уравнений:
Rb b x N s As Rsc As
1
Rs
2
1
s
1
R
9. Проверка прочности сечений с симметричным армированием.
Проверку прочности прямоугольных сечений с симметричной арматурой (Rs As= Rs A’s)проводят из условия равенства нулю суммы моментов относительно центра тяжести
растянутой арматуры Ms = 0:
N
M Rb b x h0 0.5 x Rsc A's h0 a'
2
Высота сжатой зоны x находится из условия равенства 0 суммы всех продольных сил.
x
N
n h0
Rbb
При n > R
где
n
N
Rb b h0
x h0
n 1 R 2 s R
1 R 2 s
s
Rs As
Rb b h0
R определяется как для изгибаемого элемента.
10. Порядок подбора арматуры по СП.
1. Определяем величинуn
N
Rb b h0
2. При n R
m1 n 1 n
R b h0
2
As As ' b
Rs
1
3. При n > R
m1 1
R b h0
2
As As ' b
R sc
1
где
n 1 R 2 s R
1 R 2 s
s m1
a'
h0
h 0 a'
2
R b b h 02
M N
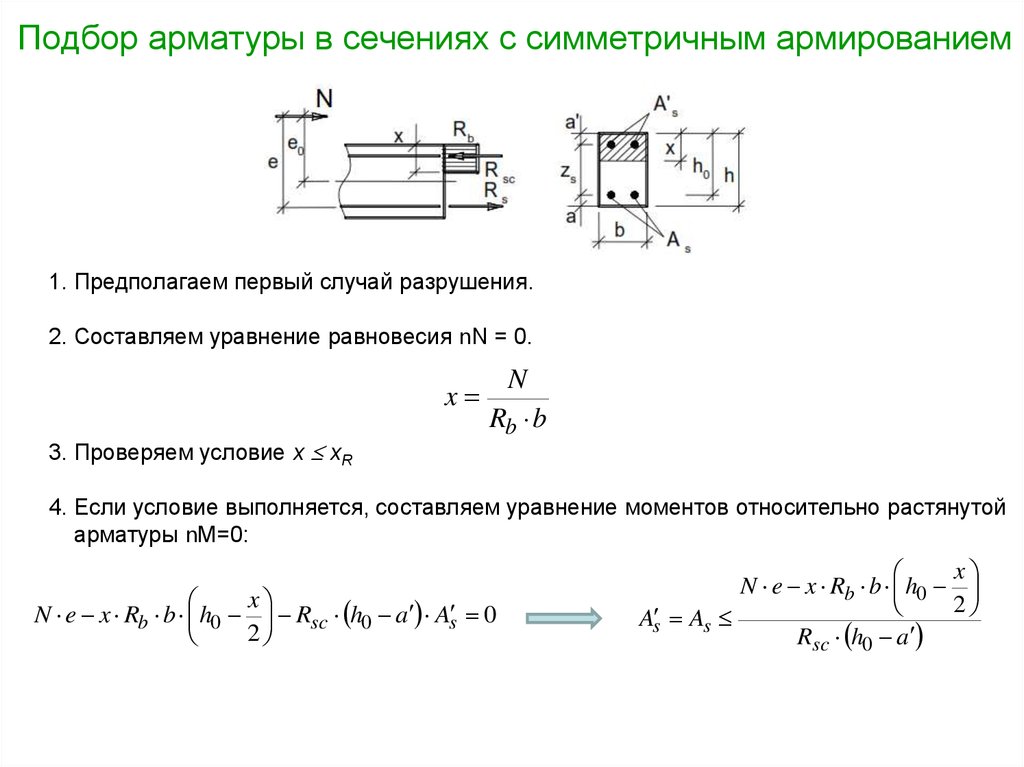
11. Подбор арматуры в сечениях с симметричным армированием
1. Предполагаем первый случай разрушения.2. Составляем уравнение равновесия nN = 0.
x
3. Проверяем условие х хR
N
Rb b
4. Если условие выполняется, составляем уравнение моментов относительно растянутой
арматуры nM=0:
x
N e x Rb b h0 Rsc h0 a As 0
2
x
N e x Rb b h0
2
As As
Rsc h0 a
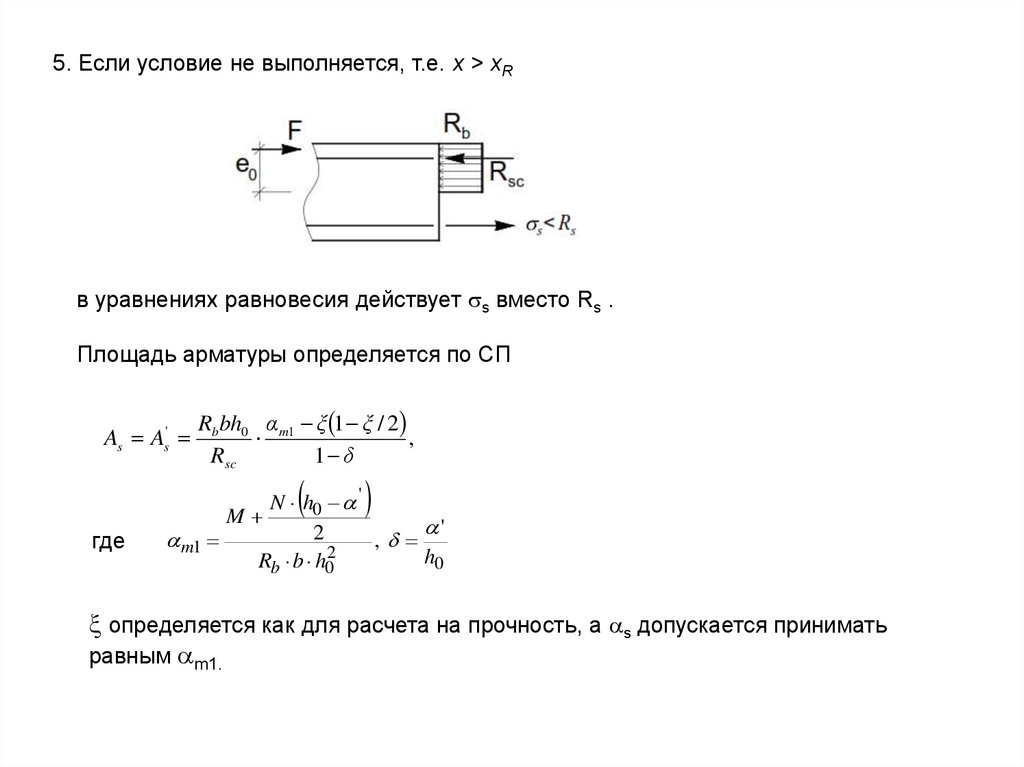
12.
5. Если условие не выполняется, т.е. х > хRв уравнениях равновесия действует s вместо Rs .
Площадь арматуры определяется по СП
As As'
Rb bh0 α m1 ξ 1 ξ / 2
,
Rsc
1 δ
где
N h0 '
M
'
2
m1
,
h0
Rb b h02
определяется как для расчета на прочность, а s допускается принимать
равным m1.
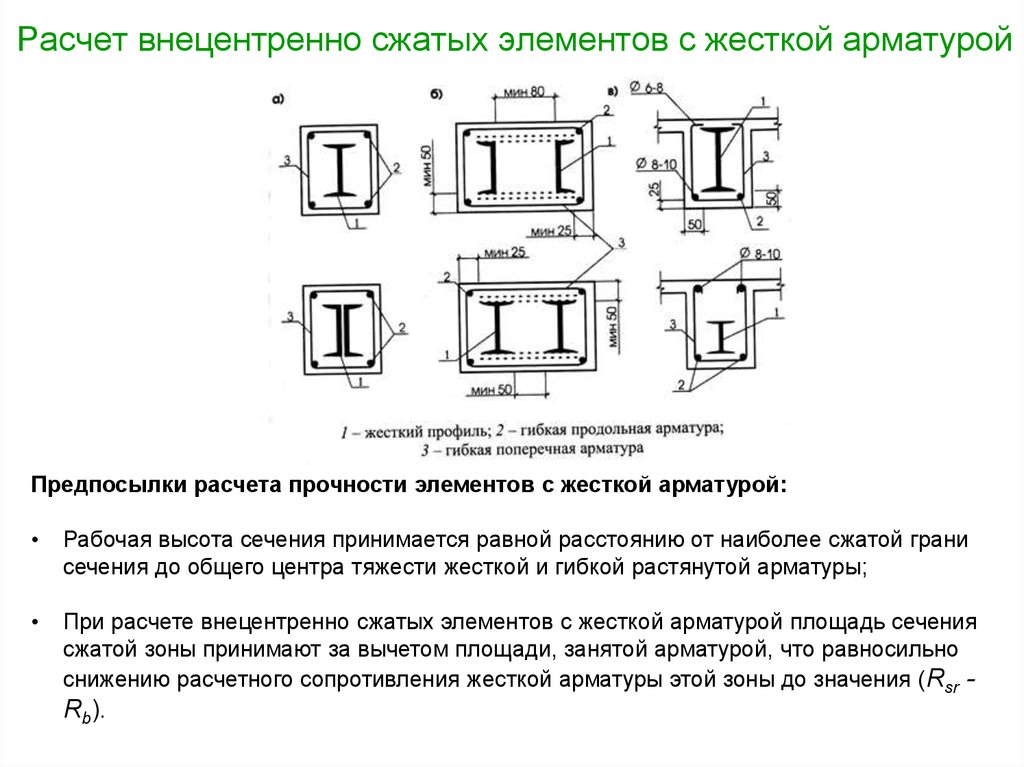
13. Расчет внецентренно сжатых элементов с жесткой арматурой
Предпосылки расчета прочности элементов с жесткой арматурой:Рабочая высота сечения принимается равной расстоянию от наиболее сжатой грани
сечения до общего центра тяжести жесткой и гибкой растянутой арматуры;
При расчете внецентренно сжатых элементов с жесткой арматурой площадь сечения
сжатой зоны принимают за вычетом площади, занятой арматурой, что равносильно
снижению расчетного сопротивления жесткой арматуры этой зоны до значения (Rsr -
Rb).
14.
При учете влияния продольного изгиба жесткость элемента определяется поформуле:
D
0.15 Eb I
0.7 Es I s sr I sr
l 0.3 e
sr
E sr
Eb
Isr – момент инерции жесткой арматуры.
Условие прочности элементов с жесткой арматурой ( Ms = 0):
N
N e1 Rb b x h0 0.5 x Rsc A' s h0 a' Rsr Rb Asr,c h0 ar
2
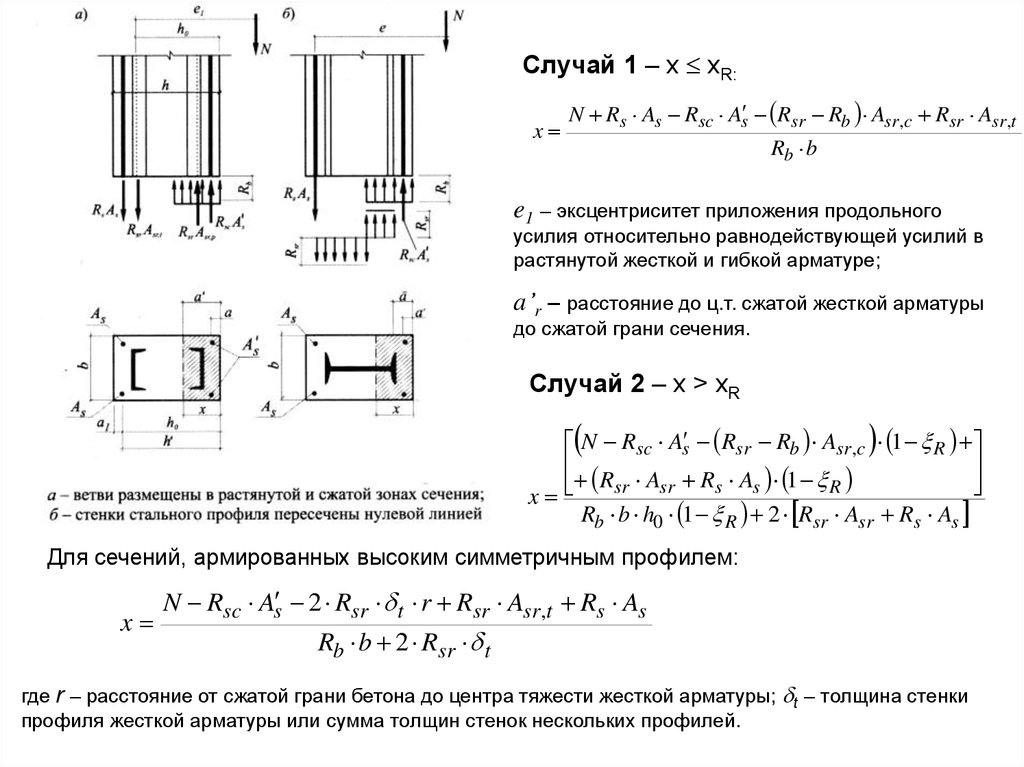
e1 – эксцентриситет приложения продольного усилия относительно
равнодействующей усилий в растянутой жесткой и гибкой арматуре;
a’r – расстояние до ц.т. сжатой жесткой арматуры до сжатой грани сечения.
15.
Случай 1 – x xR:x
N Rs As Rsc As Rsr Rb Asr,c Rsr Asr,t
Rb b
e1 – эксцентриситет приложения продольного
усилия относительно равнодействующей усилий в
растянутой жесткой и гибкой арматуре;
a’r – расстояние до ц.т. сжатой жесткой арматуры
до сжатой грани сечения.
Случай 2 – x > xR
N Rsc As Rsr Rb Asr ,c 1 R
Rsr Asr Rs As 1 R
x
Rb b h0 1 R 2 Rsr Asr Rs As
Для сечений, армированных высоким симметричным профилем:
x
N Rsc As 2 Rsr t r Rsr Asr,t Rs As
Rb b 2 Rsr t
где r – расстояние от сжатой грани бетона до центра тяжести жесткой арматуры; t – толщина стенки
профиля жесткой арматуры или сумма толщин стенок нескольких профилей.
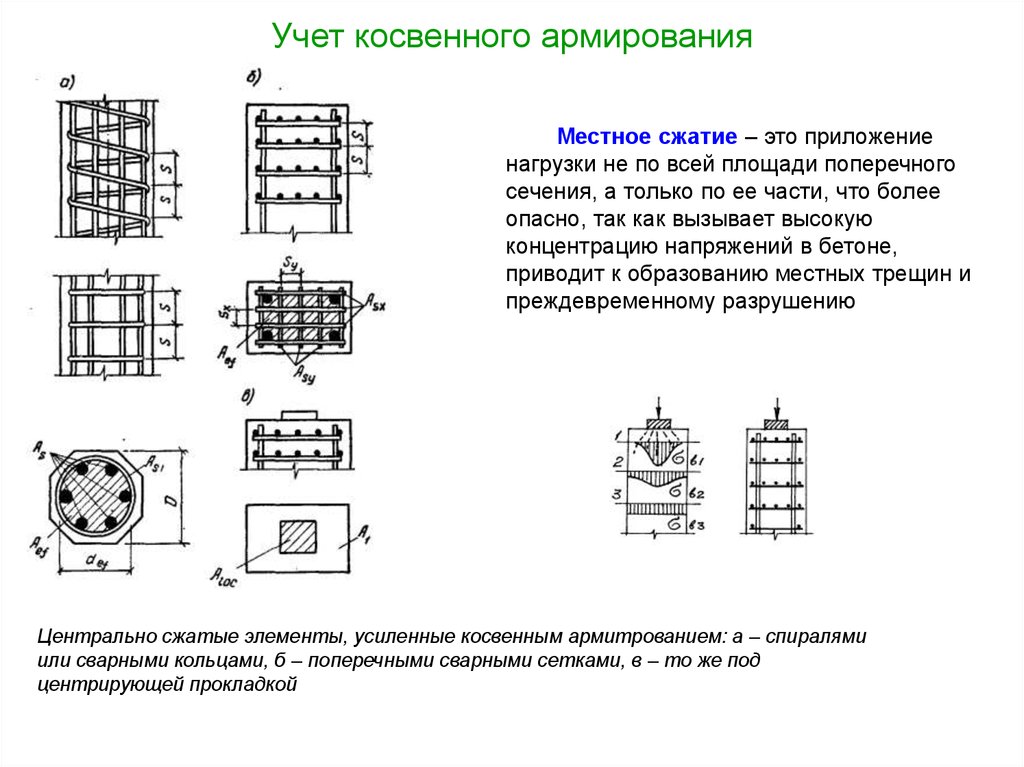
16. Учет косвенного армирования
Местное сжатие – это приложениенагрузки не по всей площади поперечного
сечения, а только по ее части, что более
опасно, так как вызывает высокую
концентрацию напряжений в бетоне,
приводит к образованию местных трещин и
преждевременному разрушению
Центрально сжатые элементы, усиленные косвенным армитрованием: а – спиралями
или сварными кольцами, б – поперечными сварными сетками, в – то же под
центрирующей прокладкой
17.
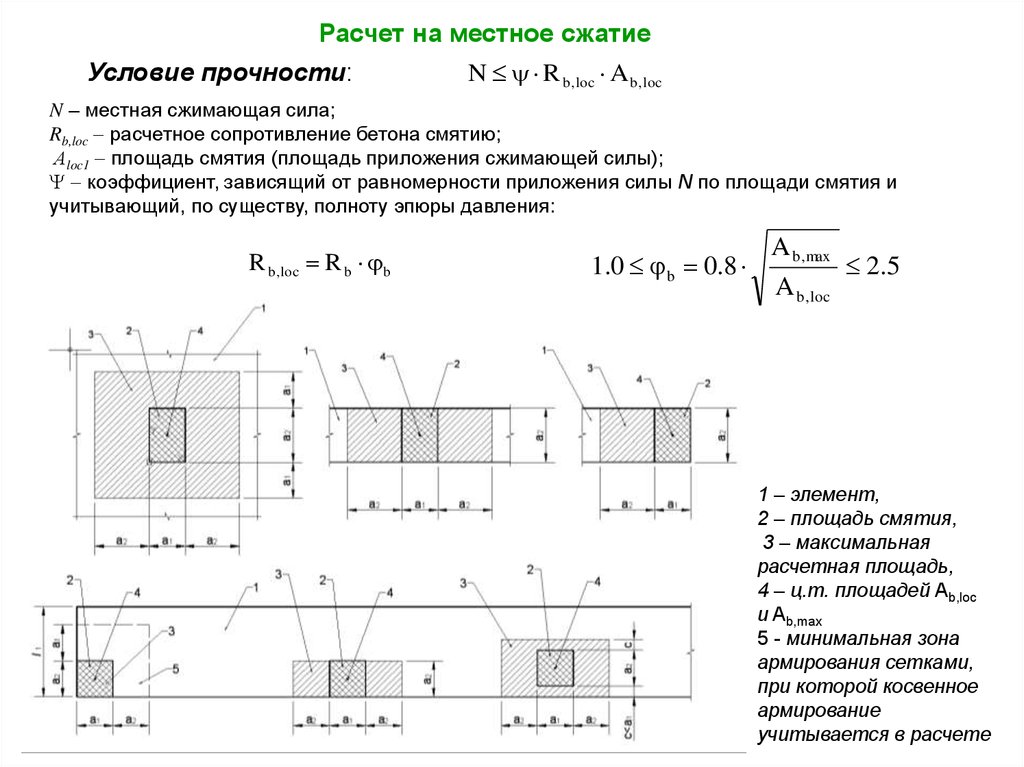
Расчет на местное сжатиеУсловие прочности:
N R b,loc A b,loc
N – местная сжимающая сила;
Rb,loc расчетное сопротивление бетона смятию;
Аloc1 площадь смятия (площадь приложения сжимающей силы);
коэффициент, зависящий от равномерности приложения силы N по площади смятия и
учитывающий, по существу, полноту эпюры давления:
R b ,loc R b b
1.0 b 0.8
A b , max
A b ,loc
2.5
1 – элемент,
2 – площадь смятия,
3 – максимальная
расчетная площадь,
4 – ц.т. площадей Ab,loc
и Ab,max
5 - минимальная зона
армирования сетками,
при которой косвенное
армирование
учитывается в расчете
18.
При наличии косвенной арматуры в виде сварных сеток вместо Rb,loc в условие прочностиподставляется Rbs,loc - расчетное сопротивление бетона сжатию, приведенное с учетом
косвенной арматуры:
Rbs,loc Rb,loc 2 s, xy Rs, xy s, xy 2 Rb,loc
s , xy - коэффициент, определяемый по формуле
s , xy
A b ,loc,ef
A b ,loc
Ab,loc,ef – площадь, заключенная внутри контура сеток косвенного армирования (считая
по их крайним стержням), но не превышающая Ab,max.
Rs,xy – расчетное сопротивление растяжению косвенной арматуры;
xy – коэффициент косвенного армирования:
xy
nx Asx l x n y Asy l y
Ab,loc ,ef s
nx, Asx, lx – число стежней, площадь сечения и длина стержня, считая в осях крайних
стержней, в направлении x;
ny, Asy, ly – то же в направлении y;
s – шаг сеток косвенного армирования.
19. Расчет условно центрально сжатых элементов
при эксцентриситете силы меньше eq < h/30 и гибкости колонны l0/h <20Условие прочности:
N Rb Ab Rsc As,tot
где
Аb – площадь сечения колонны;
As,tot – площадь всей продольной арматуры в сечении колонны;
φ - коэффициент, принимаемый по таблице 6.1 СП 52-101-2003 в зависимости от гибкости
l0/h элемента,
Требуемая площадь арматуры :
N
As ,tot
Rb Ab
Rsc
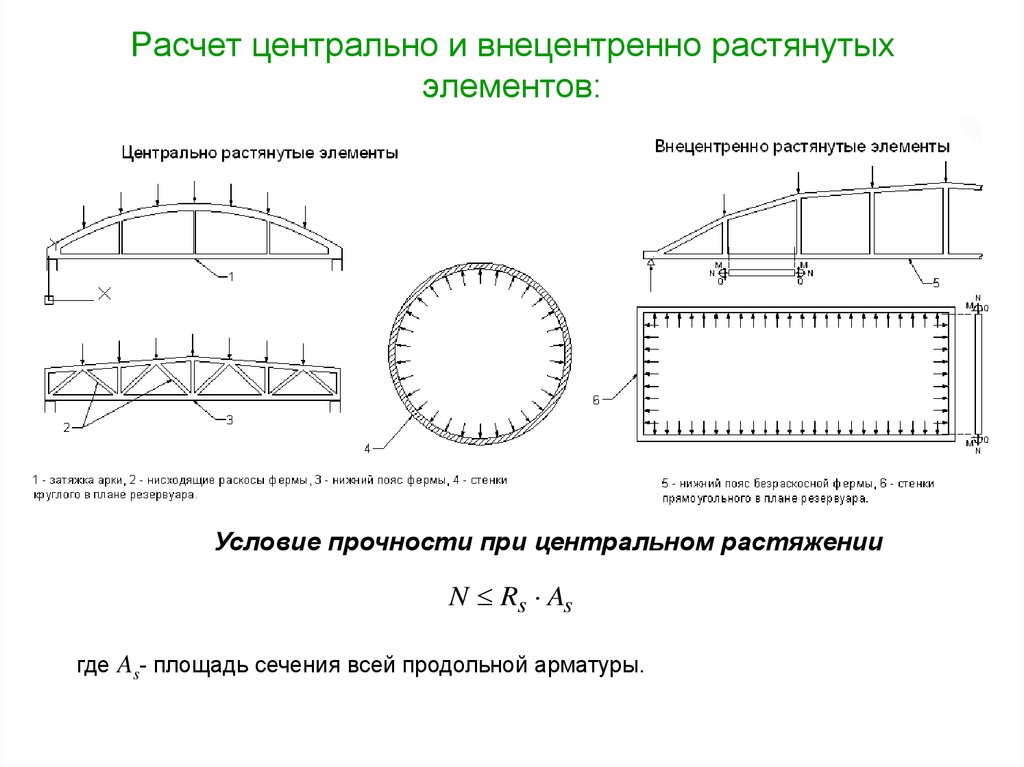
20. Расчет центрально и внецентренно растянутых элементов:
Условие прочности при центральном растяженииN Rs As
где As- площадь сечения всей продольной арматуры.
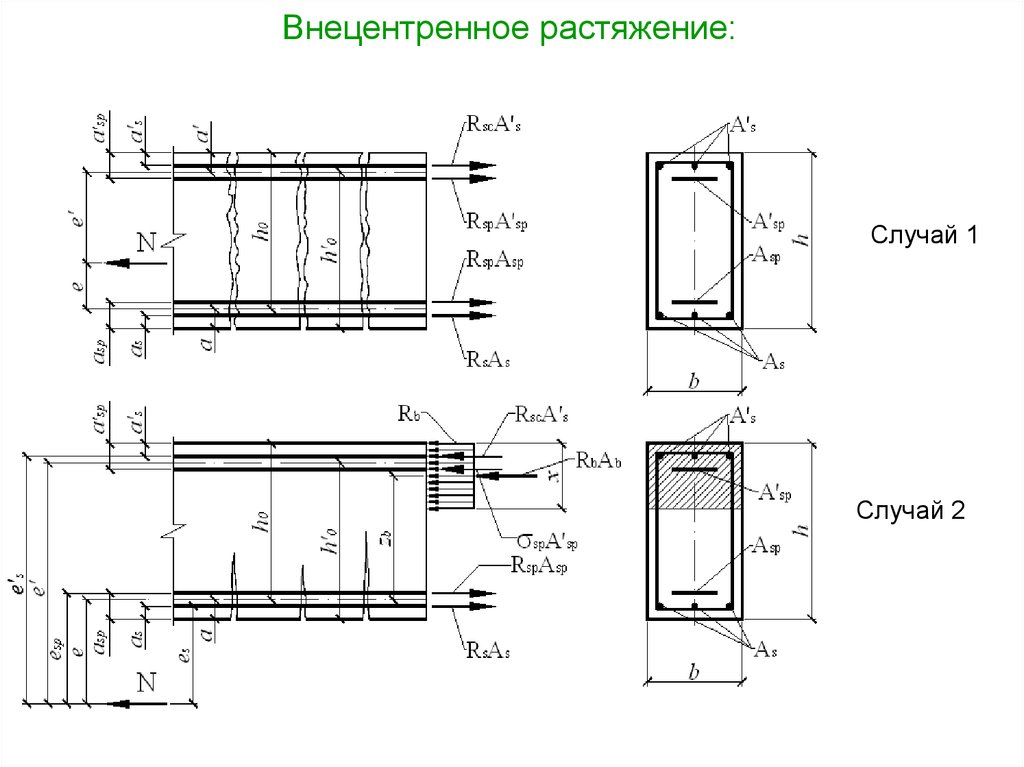
21.
Внецентренное растяжение:Случай 1
Случай 2
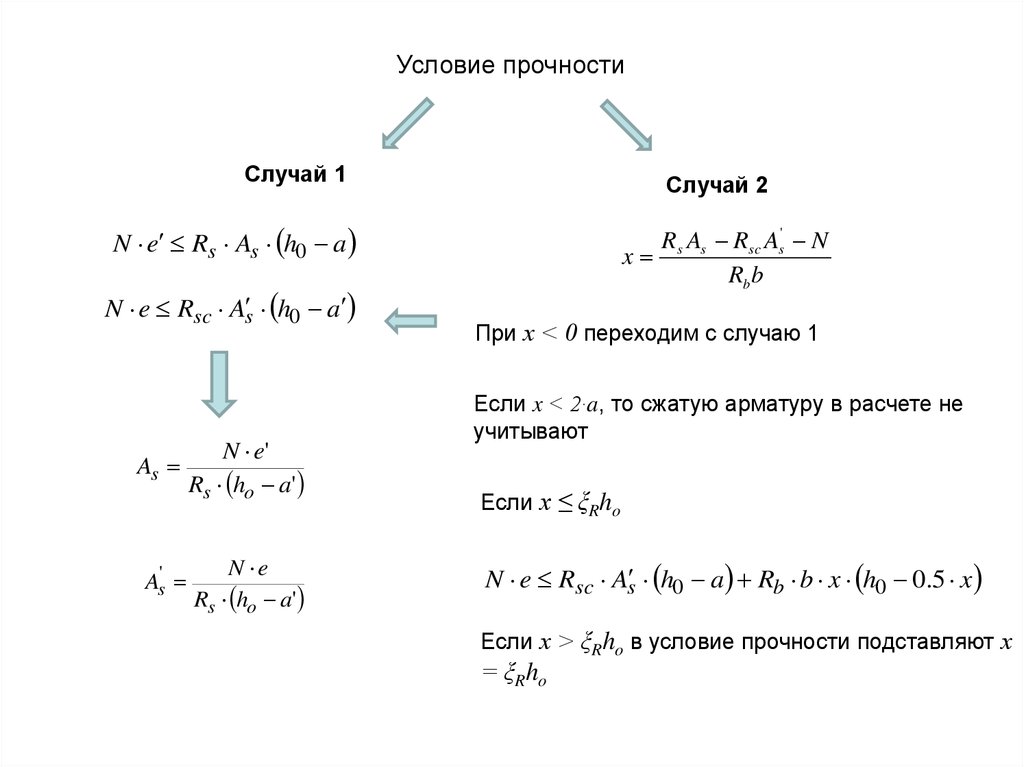
22.
Условие прочностиСлучай 1
Случай 2
N e Rs As h0 a
N e Rsc As h0 a
As
As'
N e'
Rs ho a'
N e
Rs ho a'
Rs As Rsc As' N
x
Rb b
При х < 0 переходим с случаю 1
Если x < 2∙a, то сжатую арматуру в расчете не
учитывают
Если х ≤ ξRho
N e Rsc As h0 a Rb b x h0 0.5 x
Если х > ξRho в условие прочности подставляют х
= ξRho








 Construction
Construction








