Similar presentations:
Расчет элементов прямоугольного сечения с одиночной арматурой. (Тема 9)
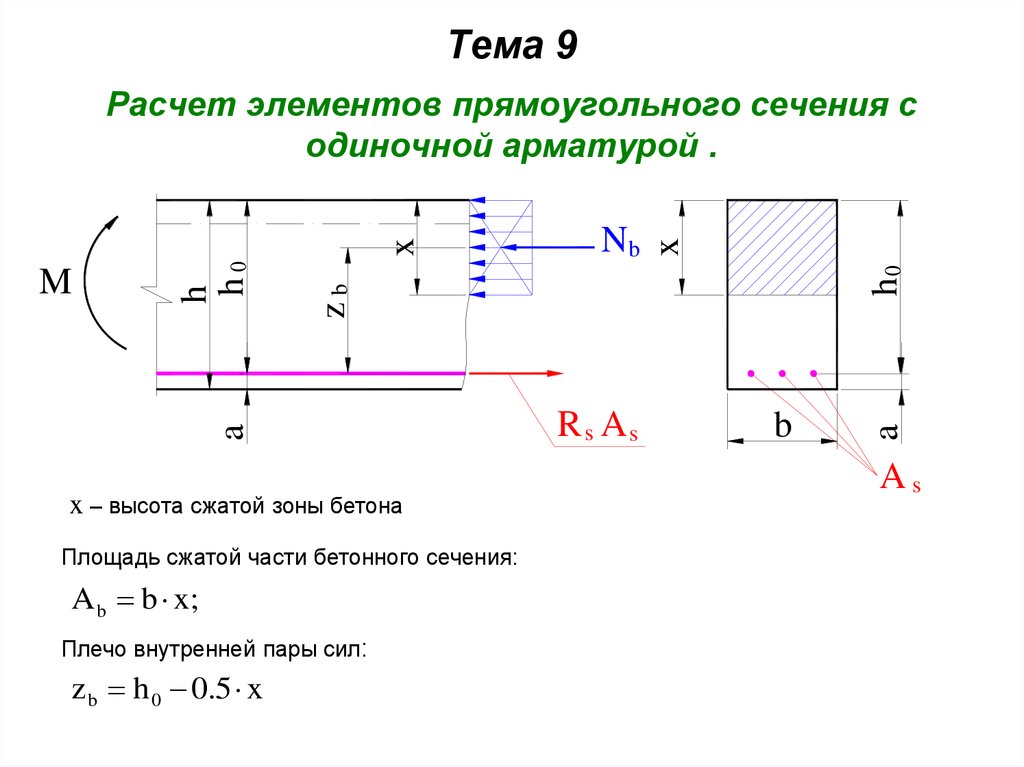
1. Тема 9 Расчет элементов прямоугольного сечения с одиночной арматурой .
Тема 9x – высота сжатой зоны бетона
Площадь сжатой части бетонного сечения:
A b b x;
Плечо внутренней пары сил:
z b h 0 0.5 x
R s As
b
a
h
x
Nb
zb
a
M
h
h
x
Расчет элементов прямоугольного сечения с
одиночной арматурой .
As
2.
Сумма проекций всех сил на ось X равна 0.R s As b x R b 0
Если
x xR -
отсюда
x
R s As
Rb b
1 случай разрушения.
Сумма моментов относительно растянутой арматуры:
Ms 0
M R b b x h 0 0.5 x ;
Сумма моментов относительно центра сжатой зоны бетона:
Mb 0
M R s As h 0 0.5 x ;
Условие прочности:
x
M Rb b x h0 0.5 x Rb b h02
h0
x
1 0.5 Rb b h02 m
h0
3.
гдеx
m
h0
0.5 x
1 0.5
1
h0
Плечо внутренней силы выражаем через коэффициент
0.5 x
h 0
z b h 0 0.5 x h 0 1
h0
Тогда уравнения равновесия примут вид:
R b b h 0 R s As ;
M R s As h 0
M m R b b h 02 ;
где
zb
h0
4.
Еслиx > xR -
2 случай разрушения.
В переармированных сечениях (из бетона класса не выше В30 и с арматурой из
мягких сталей) при увеличении количества арматуры увеличение высоты сжатой
зоны и несущей способности существенно замедляется.
Поэтому допускается принимать:
M Rb b x R h0 0.5 x R Rb b h02 R
5. Порядок расчета на прочность:
Предполагаем, что у нас первый случай разрушения.R s As
Rb b
1. Находим величину
x
2. Сравниваем величину
с величиной R.
,и
x
h0
Класс арматуры
А240
А300
А400
А500
В500
R
0.612
0.577
0.531
0.493
0.502
R
0.425
0.411
0.390
0.372
0.376
3. При
x R h 0
должно выполняться условие
M R s A s h 0 0.5 x
(В этом случае прочность обеспечена.)
4. При
x R h 0
должно выполняться условие
M R R b h 02
6. Порядок подбора арматуры
1. Предполагаем первый случай разрушения. Составляем уравнение равновесиямоментов относительно ц.т. растянутой арматуры nM =0, приравняв M=Mu.
M M u Rb b x h0 0.5 x
2. Находим из этого уравнения высоту сжатой зоны x.
3. При x R h0 составляем уравнение равновесия nN =0:
Rs As b x Rb 0
As
b x Rb
Rs
Или из суммы относительно ц.т. сжатой зоны бетона
As
4. При
M
;
Rs h0 0.5 x
x R h0 увеличиваем класс бетона или размеры сечения, или ставим
арматуру в сжатой зоне.
7. Порядок подбора арматуры по таблицам:
1. Вычисляем величину2. Если
m R
Тогда
As
3. Если
m R
m
M
R b b h 02
находим
1 1 1 2 m
R b b h0
Rs
требуется увеличить размеры сечения, повысить класс бетона или установить
сжатую арматуру.
8. Расчет прочности изгибаемых элементов прямоугольного профиля с двойной арматурой
Элементы с двойной арматурой – это элементы, в которых арматуру порасчету устанавливают и в растянутой и в сжатой зонах.
Сжатую арматуру устанавливают:
• когда прочность бетона недостаточна, т.е.
бетона и размеров сечения невозможно;
x R h 0
, а увеличение класса
• при воздействии изгибающего момента двух знаков (неразрезные балки, ригели
рам) или знакопеременных нагрузок;
• для уменьшения эксцентриситета от обжатия предварительно напряженных
элементов.
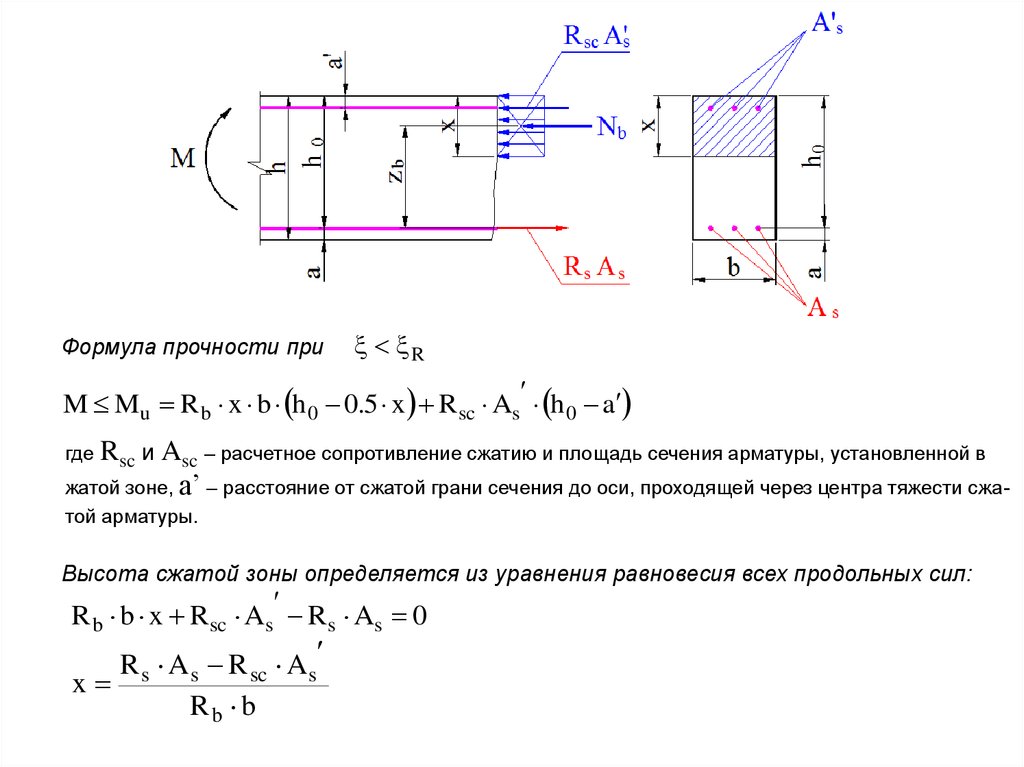
9.
Формула прочности приR
M Mu R b x b h 0 0.5 x R sc As h 0 a
Rsc и Asc – расчетное сопротивление сжатию и площадь сечения арматуры, установленной в
жатой зоне, а’ – расстояние от сжатой грани сечения до оси, проходящей через центра тяжести сжагде
той арматуры.
Высота сжатой зоны определяется из уравнения равновесия всех продольных сил:
R b b x R sc As R s As 0
R s A s R sc A s
x
Rb b
10.
При x R h0 - второй случай разрушенияzb
Nb
s R s )A s
a
M
h
h
x
a'
R sс A sс
В этом случае для бетонов класса
не выше В30 и арматуры классов А400 и
А500 применяются те же формулы
прочности с заменой x на xR:
M M u Rb x R b h0 0.5 x R
R A h a
sc
s
Если величина сжатой зоны x
2 a’, то изменяется напряженное
состояние в сечении
0
В этом случае, если приближенной
принять z = zs (расстояние между
растянутыми и сжатыми стержнями), то
из условий равновесия получим:
M 0
M u Rs As zs
При M < Mu прочность обеспечена.
11. Порядок расчета на прочность:
1. Из уравнения равновесия nN = 0 находим высоту сжатой зоны бетона:Rs As Rsc As
x
Rb b
2. Сравниваем величину
3. При
,и
x
.
h0
с величиной R.
x R h 0 должно выполняться условие:
M Rb x b h0 0.5 x Rsc As h0 a
4. При
x R h 0
должно выполняться условие
M R Rb h02 Rsc As h0 a
5. При
x 2 a должно выполняться условие:
M M u Rs As z s
12. Порядок подбора сжатой арматуры:
1. Найти предельный момент, который может воспринять прямоугольное сечение содиночной арматурой в растянутой зоне:
M umax Rb b x R h0 0.5 x R
2. Найти максимальную одиночную арматуру, соответствующую этому моменту:
As
3. Найти разницу моментов
b xR Rb
Rs
M M M umax
4. Чтобы воспринять этот момент поставить в сжатую зону дополнительную арматуру.
Из условия равновесия моментов относительно растянутой арматуры:
M Rsc As z s
Asc As
M
Rsc z s
13. Порядок подбора арматуры по нормам:
m1. Вычисляем величину
2. Если m R
M
R b b h 02
находим 1 1 2 m
Сжатая арматура по расчету не требуется.
3. Если
m R ,
M R R b b h 02
As
.
R s h 0 a
M A s R sc b h 0 a
Уточняем m
R b b h 02
R R b b h 0
As
As
Rs
Тогда
As
R b b h0
Rs
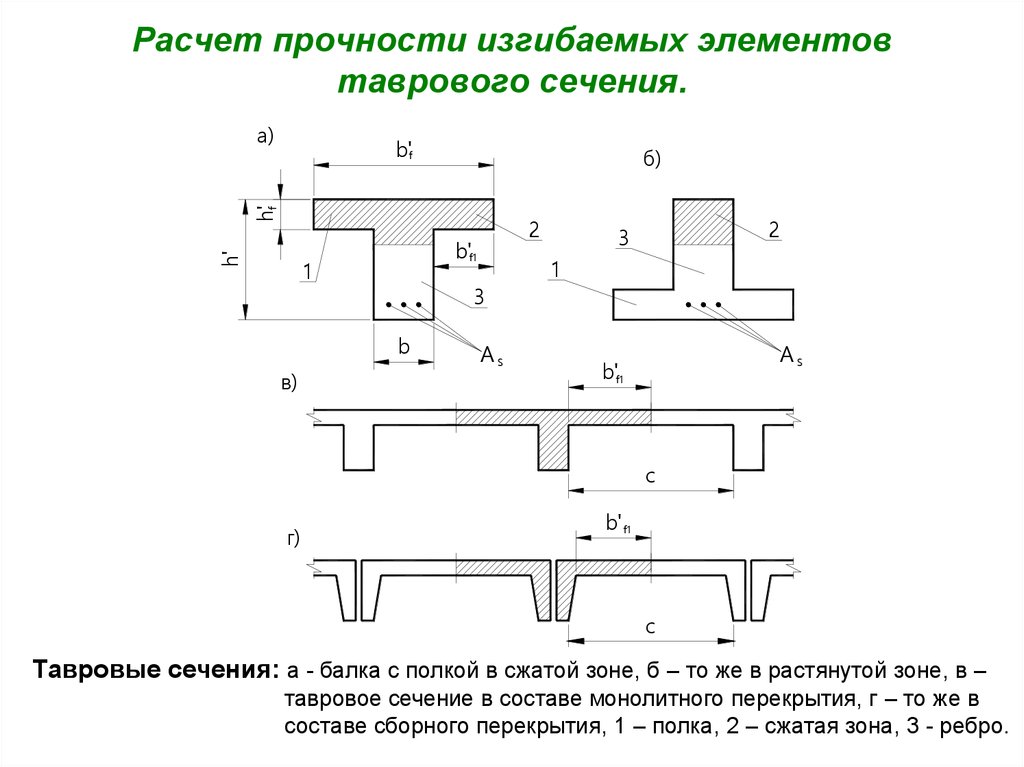
14. Расчет прочности изгибаемых элементов таврового сечения.
а)b'f
h'
h'f
б)
b'f1
1
2
3
1
3
b
в)
2
AS
AS
b'f1
c
г)
b' f1
c
Тавровые сечения: а - балка с полкой в сжатой зоне, б – то же в растянутой зоне, в –
тавровое сечение в составе монолитного перекрытия, г – то же в
составе сборного перекрытия, 1 – полка, 2 – сжатая зона, 3 - ребро.
15.
При большой ширине полок участки свесов, более удаленные от ребра напряженыменьше. Поэтому в расчет вводят эквивалентную ширину свесов полки:
bf b 2 bf 1
Ширина свеса полки в каждую сторону от ребра принимается не более 1/6 пролета:
а) при наличии поперечных ребер или при
h f 0.1 h не более 1/2 расстояния в свету
между продольными ребрами;
б) при отсутствии поперечных ребер (или при расстояниях между ними больших, чем
расстояния между продольными ребрами) и
h f 0.1 h – не более 6 h f ;
в) при консольных свесах полки:
• при
• при
• при
h f 0.1 h - не более 6 h f ;
0.05 h h f 0.1 h - не более 3 h f ;
h 0.05 h - свесы не учитываются.
f
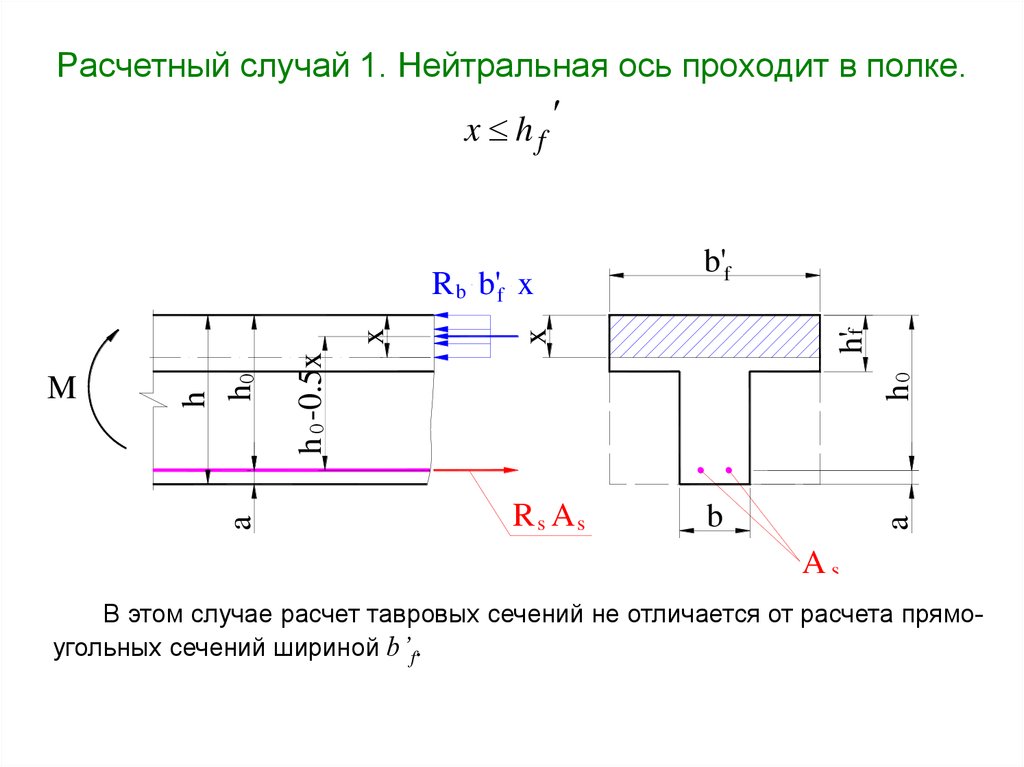
16. Расчетный случай 1. Нейтральная ось проходит в полке.
x hf
h'f
x
h
h -0.5x
R s As
b
a
a
M
h
h
x
R b b'f x
b'f
As
В этом случае расчет тавровых сечений не отличается от расчета прямоугольных сечений шириной b’f.
17.
Условие прочности:M Mu R b bf x h 0 0.5 x
или
M Mu R b bf h 02 m
Высота сжатой зоны определяется из выражения:
R b bf x R s As 0
откуда
R s As
x
R b
b
Заменив
f
x
на
h 0 получим уравнение:
R b bf h 0 R s As 0
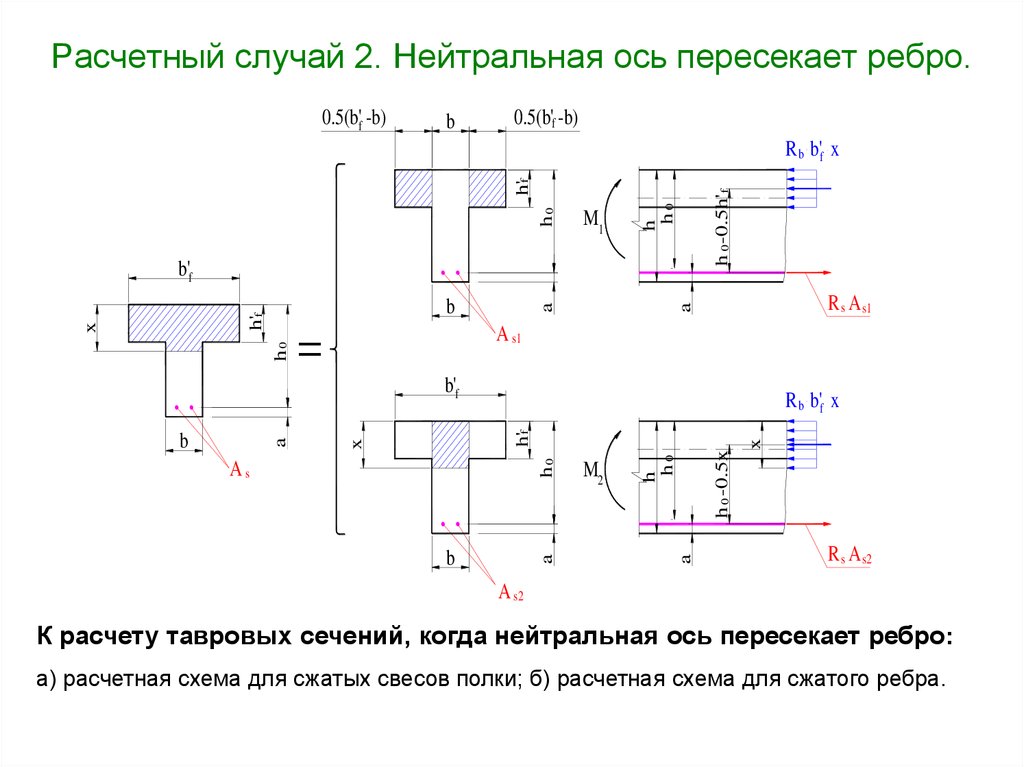
18. Расчетный случай 2. Нейтральная ось пересекает ребро.
0.5(b'f -b)b
0.5(b'f -b)
h -0.5h' f
M1
h
h
h
h'f
R b b'f x
h
x
h'f
a
b
R s A s1
a
b'f
A s1
b'f
a
b
h -0.5x
M2
a
As
h
h
h
x
h'f
x
a
b
R b b'f x
R s A s2
A s2
К расчету тавровых сечений, когда нейтральная ось пересекает ребро:
а) расчетная схема для сжатых свесов полки; б) расчетная схема для сжатого ребра.
19.
Условие прочности:M Mu M1 M2 R b bf b h f h 0 0.5 h f R b b x h 0 0.5 x
Высота сжатой зоны определяется из уравнения равновесия
Nx 0 , при этом
A s A s1 A s 2
R b bf b h f R b b x R s As 0
Используя соотношение x h 0
формулы прочности преобразуются к виду:
M M u R b b f b h f h 0 0.5 h f m R b b h 02
R b b f b h f R b b h 0 R s A s 0
20. Определение положения нейтральной оси.
h'fh
x
x
b
a
R s As
a
h
h
M
h -0.5h'f
R b b'f x
b'f
As
Если изгибающий момент от расчетных нагрузок оказывается меньше момента внутренних сил, воспринимаемых сжатой полкой таврового сечения, относительного центра
тяжести растянутой арматуры или равен ему, то нейтральная ось проходит в полке, т.е.
M Mu R b bf h f h 0 0.5 h f
x hf
Если условие не выполняется, то нейтральная ось пересекает ребро.
21.
Если изгибающий момент от расчетных нагрузок неизвестен, но известны вседанные о сечении, включая площадь растянутой арматуры As, положение нейтральной
оси необходимо определять из суммы проекций всех сил на продольную ось элемента
Nx 0
Полагается, что ось проходит по нижней грани полки:
R s As R b bf h f
Если условие выполняется, нейтральная ось проходит в полке
22. Порядок расчета на прочность тавровых сечений:
1. Проверяем условиеR s As R b bf h f R sc As .
2. Если условие выполняется, то граница сжатой зоны проходит в полке, и считаем
как прямоугольное сечение шириной bf ’.
3. Если условие не выполняется, и граница сжатой зоны проходит в ребре, то определяем высоту сжатой зоны бетона по формуле:
R s As R sc As R b b f b h f
x
Rb b
4. Если x R h 0 проверяем прочность сечения по условию:
M Mult R b b x h 0 0.5 x R b bf b h f h 0 0.5 h f R sc As h a
5. Если
x R h 0
принимаем
x R h 0
23.
Порядок подбора арматуры в тавровых сечениях:1. Предполагаем 1 случай разрушения (т.е. не учитываем сжатую арматуру). Проверяем
условие:
M R b h h 0.5 h
b
f
f
0
f
2. Если условие выполняется, то граница сжатой зоны проходит в полке, и подбор
арматуры проводится как для прямоугольного сечения шириной bf’.
3. Если условие не выполняется, то определяем момент, воспринимаемый свесами
полок (относительно растянутой арматуры):
M ov Rb b f b h f h0 0.5 h f
4. Найдем продольную арматуру, необходимую для восприятия момента (из суммы
продольных сил)
Rb b f b h f
As,ov
Rs
5. Найдем момент воспринимаемый ребром: M web M M ov
6. Подбор арматуры в ребре проводим как для прямоугольного сечения на момент Mweb
M web
m
Rb b h02
7. Если
m R находим As,web
8. Если
m R имеем второй случай разрушения и либо увеличиваем класс бетона
As As,web As,ov
или размеры сечения, либо устанавливаем сжатую арматуру.
24. Порядок подбора арматуры в тавровых сечениях по нормам:
1. Площадь сжатой арматуры подбираем из условия (предполагая, что нейтральнаяось проходит в ребре):
M R R b b h 02 R b b f b h f h 0 0.5 h f
As
R sc h 0 a
2. Проверяем условие
M R b bf h f h 0 0.5 h f R sc As h 0 a
3. Если условие выполняется, то граница сжатой зоны проходит в полке, и подбор
арматуры проводится как для прямоугольного сечения шириной bf ’.
4. Если условие не выполняется, то площадь растянутой арматуры определяется по
формуле:
R b b h 0 1 1 2 m R b b f b h f R sc A s
As
Rs
где
Если
m
M R b b f b h f h 0 0.5 h f R sc A s h 0 a
R b b h 02
m R , требуется увеличить размеры сечения, повысить класс бетона.



















 Construction
Construction








