Расчет прочности изгибаемых элементов по наклонным сечениям. (Тема 10)

1. Тема 10 Расчет прочности изгибаемых элементов по наклонным сечениям

Разрушение происходит по одной из трех схем:
а) Раздавливание тонкой стенки (ребра) по наклонной полосе между трещинами от
действия главных сжимающих напряжений mc ;
б) Взаимный сдвиг двух частей изгибаемого элемента, разделенных наклонной
трещиной под действием поперечной силы Q;
О двух частей изгибаемого элемента, разделенных наклонной трещиной, который вызывается действием изгибающего момента М .
в) Взаимный поворот относительно точки

2.

Характер разрушения изгибаемого элемента по наклонному сечению: при действии
сосредоточенных сил; при загружении конструкции равномерно распределенной нагрузкой
1 - критическая наклонная трещина, 2 – дополнительные наклонные трещины, 3 – продольная
трещина, 4 – раздавленный участок сжатой зоны бетона, с – расстояние от внутренней грани опоры
до вершины до вершины наклонной трещины.

3.

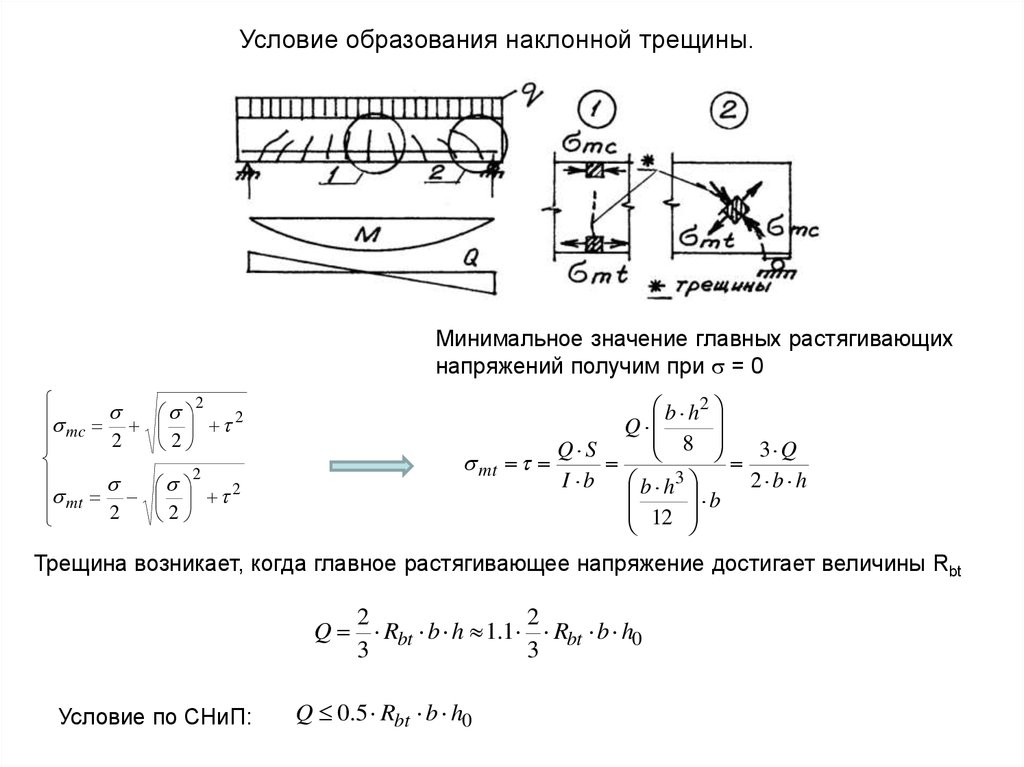
Условие образования наклонной трещины.
Минимальное значение главных растягивающих
напряжений получим при = 0
mc
2
mt
2
b h2
Q
8
Q S
3 Q
mt
I b b h3
2 b h
b
12
2
2
2
2
2
2
Трещина возникает, когда главное растягивающее напряжение достигает величины Rbt
Q
Условие по СНиП:
2
2
Rbt b h 1.1 Rbt b h0
3
3
Q 0.5 Rbt b h0

4. Расчет на действие поперечной силы по наклонной полосе между трещинами.

Установлено, что предельная сила Q, воспринимаемая бетонным блоком,
пропорциональна его ширине b и рабочей высоте сечения h0.
Т.к. бетон в этом случае разрушается в основном от сжатия в расчетную
формулу вводится прочность бетона на сжатие Rb. А т.к. полоса бетона между
наклонными трещинами находится в условиях двухосного напряженного состояния
(растяжение-сжатие), то прочность бетона в этом случае будет ниже, чем при
одноосном напряженном состоянии.
Условие прочности на действие поперечной силы
Q в нормальном сечении,
расположенном не менее чем на расстоянии h0 от опоры:
Q 0.3 Rb b h0

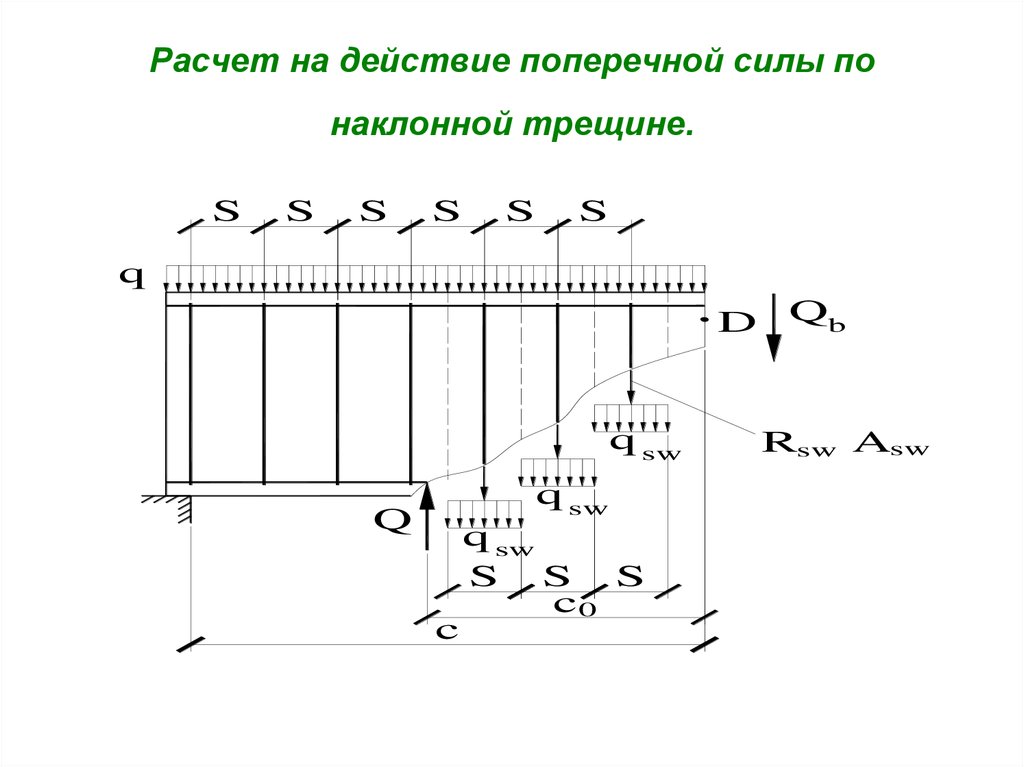
5. Расчет на действие поперечной силы по наклонной трещине.

S
S
S
S
S
S
q
D
q sw
q sw
Q
c
q sw
S S S
c0
Qb
Rsw Asw

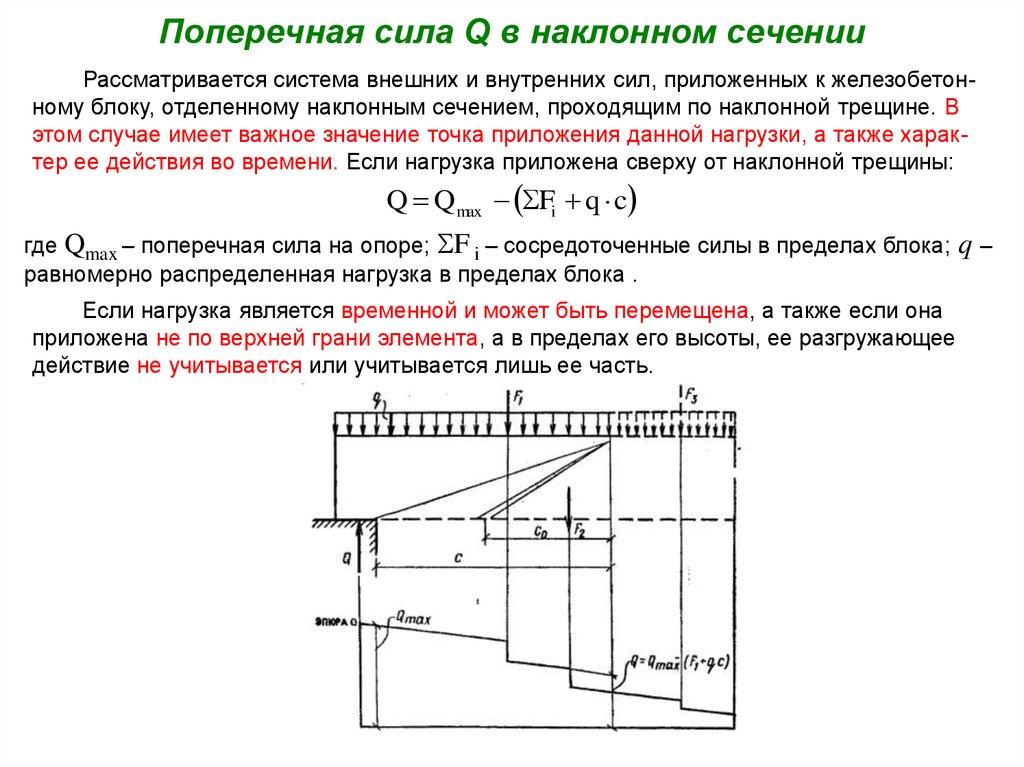
6. Поперечная сила Q в наклонном сечении

Рассматривается система внешних и внутренних сил, приложенных к железобетонному блоку, отделенному наклонным сечением, проходящим по наклонной трещине. В
этом случае имеет важное значение точка приложения данной нагрузки, а также характер ее действия во времени. Если нагрузка приложена сверху от наклонной трещины:
Q Qmax Fi q c
где Qmax – поперечная сила на опоре; F i – сосредоточенные силы в пределах блока;
равномерно распределенная нагрузка в пределах блока .
Если нагрузка является временной и может быть перемещена, а также если она
приложена не по верхней грани элемента, а в пределах его высоты, ее разгружающее
действие не учитывается или учитывается лишь ее часть.
q–

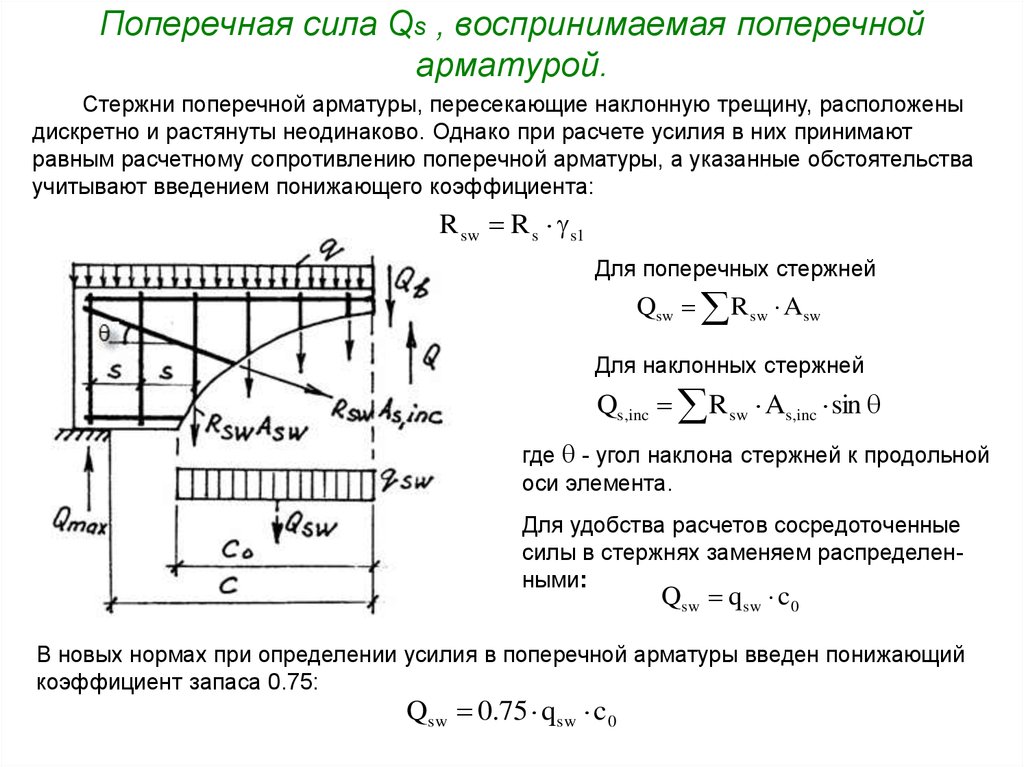
7. Поперечная сила Qs , воспринимаемая поперечной арматурой.

Стержни поперечной арматуры, пересекающие наклонную трещину, расположены
дискретно и растянуты неодинаково. Однако при расчете усилия в них принимают
равным расчетному сопротивлению поперечной арматуры, а указанные обстоятельства
учитывают введением понижающего коэффициента:
R sw R s s1
Для поперечных стержней
Qsw R sw Asw
Для наклонных стержней
Qs,inc R sw As,inc sin
где - угол наклона стержней к продольной
оси элемента.
Для удобства расчетов сосредоточенные
силы в стержнях заменяем распределенными:
Qsw q sw c 0
В новых нормах при определении усилия в поперечной арматуры введен понижающий
коэффициент запаса 0.75:
Qsw 0.75 q sw c0

8. Поперечная сила Qb , воспринимаемая бетоном.

Поперечная сила, воспринимаемая бетоном зависит от размеров сечения (b и h),
прочности бетона на растяжение Rbt, а также от так называемого пролета среза (с/h0). C
увеличением этой величины происходит резкое падение Qb приблизительно по гиперболической зависимости.
1.5 R bt b h 0 1.5 R bt b h 02 M b
Qb
c
c
c
h0
По результатам экспериментов установлено, что при малых и больших значениях
относительного пролета среза значение Qb сохраняет значения близкие к постоянным.
По нормам поперечная сила, воспринимаемая бетоном принята не более
2.5 Rbt b h0
и не менее
0.5 Rbt b h0

9. Влияние продольной силы на несущую способность.

При сжатии несущая способность сечения по поперечной силе увеличивается,
а при растяжении - наоборот, снижается.
Влияние сжимающих и растягивающих напряжений при расчете по полосе
между наклонными сечениями и по наклонным сечениям согласно СП 63.1330.2012
учитывается с помощью коэффициента φn.
при 0 σcp 0.25∙Rb;
при 0.25∙Rb σср 0.75∙Rb;
1.25
при 0.75∙Rb σср Rb;
при 0 σt 2Rbt
где σср - среднее сжимающее напряжение в бетоне от воздействия продольных сил,
принимаемое положительным.
σt - среднее растягивающее напряжение в бетоне от воздействия продольных сил,
принимаемое положительным

10. Расчетная длина проекции опасного наклонного сечения и проекция наклонной трещины

Действие распределенной нагрузки:
Случай 1
Случай 2

11.

В случае 1 длина наклонной трещины с0 совпадает с пролетом среза с. Найдем
величину пролета среза, при которой несущая способность отсеченного трещиной
элемента минимальна:
d
Q 0
dc
Mb
0.75 qsw q 0
c2
c0 c
Mb
qsw 0.75 q
В случае 2 начало и вершина опасной трещины неизвестны. Чтобы определить
положение сечения с наименьшим запасом прочности, нужно приравнять к нулю первую
производную.
При дифференцировании производная от Qsw как от постоянной величины
равна 0. в этом случае:
c
Mb
,
q
Увеличение и уменьшение наклонной трещины не может быть бесконечным, поэтому на
основе эмпирических данных ее значение ограничено: не больше 2 h0 и не меньше h0.

12. Граница между двумя случаями:

По нормам при действии равномерно распределенной нагрузки с принимается:
c
в случае если
Mb
0.75 qsw q1
Mb
2 h0
q1 1 0.5 qsw
Rbt b
или
qsw
2
Rbt b
В противном случае проекция опасного сечения принимается равной:
c
Mb
q1
Значение нагрузки q1 принимается равным q, если действует сплошная распределенная
нагрузка.
Если нагрузка q включает в себя временную нагрузку, которая приводится к эквивалентной по
моменту равномерно распределенной нагрузке qv (т.е. когда эпюра моментов М от принятой нагрузки
qv всегда огибает эпюру М от фактической временной нагрузки), то
q1 q 0.5 qv
Так как нагрузка часто бывает приложена не равномерно, а сосредоточена в отдельных
местах, то можно вычислить с по формуле (приняв q=0):
c
Mb
0.75 qsw

13.

Действие сосредоточенной силы:
Случай 2
Случай 1
c a
при a h 0
c h0
c a
c0 c
при
c0 2 h 0
Mb
c
0.75 q sw
Mb
c0
0.75 q sw
при a 2 h0
но не меньше h0
при
Mb
c
0.75 q sw
c c0
Mb
0.75 q sw
c 2 h0

14.

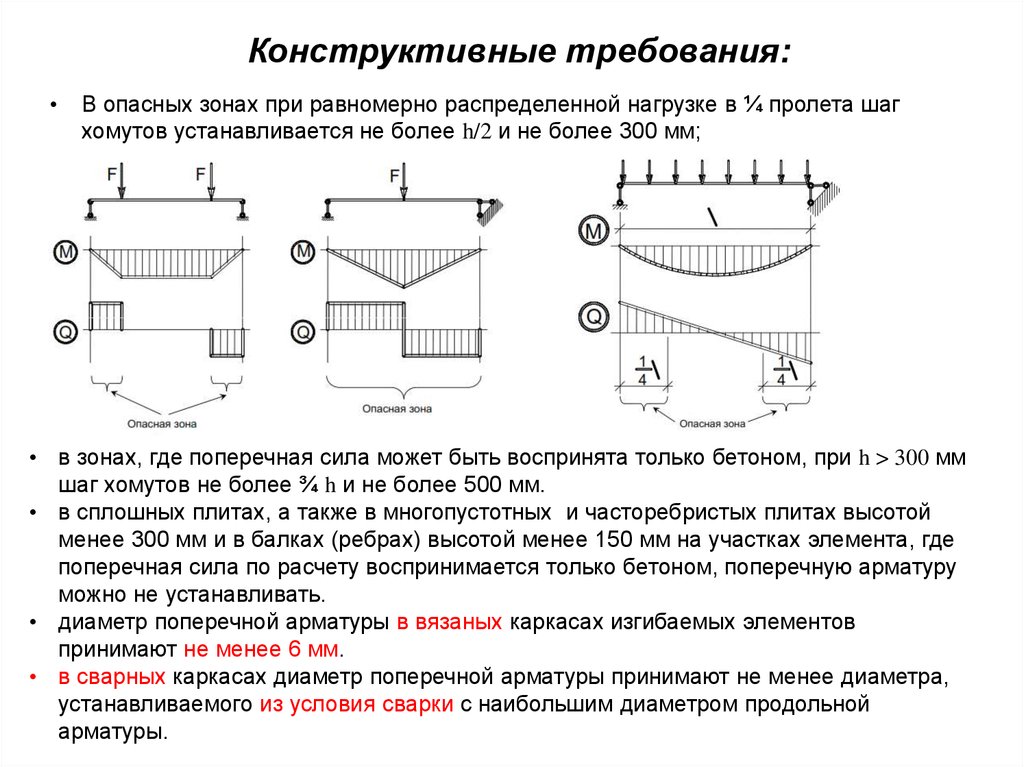
Конструктивные требования:
В опасных зонах при равномерно распределенной нагрузке в ¼ пролета шаг
хомутов устанавливается не более h/2 и не более 300 мм;
• в зонах, где поперечная сила может быть воспринята только бетоном, при h > 300 мм
шаг хомутов не более ¾ h и не более 500 мм.
• в сплошных плитах, а также в многопустотных и часторебристых плитах высотой
менее 300 мм и в балках (ребрах) высотой менее 150 мм на участках элемента, где
поперечная сила по расчету воспринимается только бетоном, поперечную арматуру
можно не устанавливать.
• диаметр поперечной арматуры в вязаных каркасах изгибаемых элементов
принимают не менее 6 мм.
• в сварных каркасах диаметр поперечной арматуры принимают не менее диаметра,
устанавливаемого из условия сварки с наибольшим диаметром продольной
арматуры.

15.

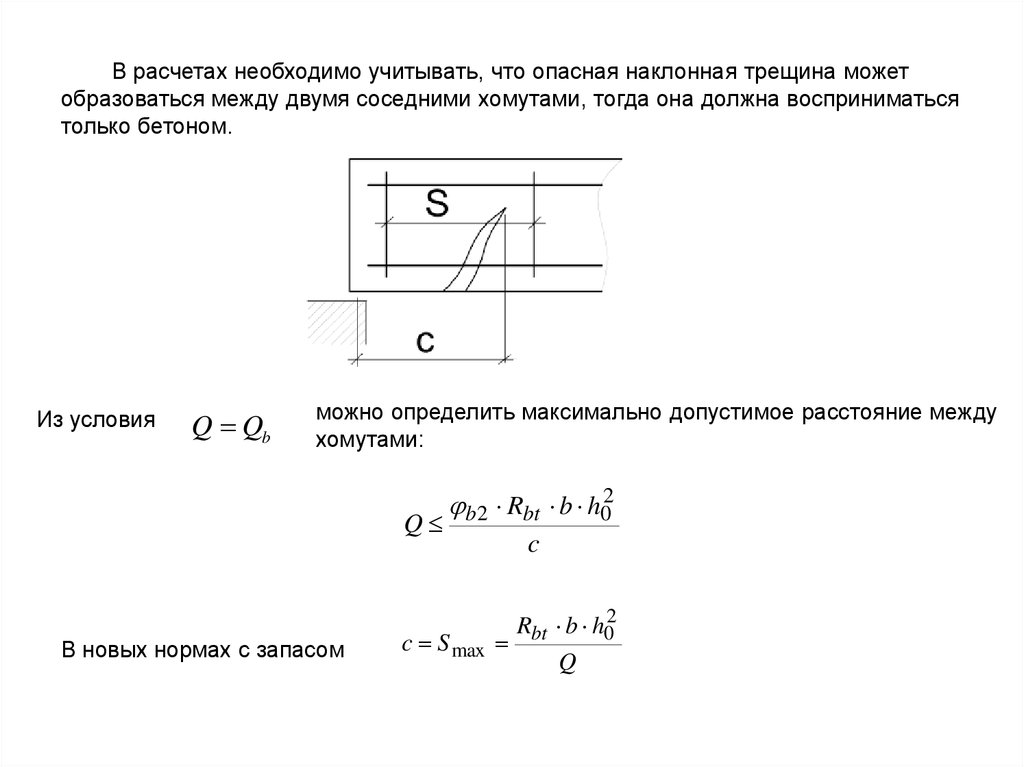
В расчетах необходимо учитывать, что опасная наклонная трещина может
образоваться между двумя соседними хомутами, тогда она должна восприниматься
только бетоном.
Из условия
Q Qb
можно определить максимально допустимое расстояние между
хомутами:
Q
В новых нормах с запасом
b2 Rbt b h02
c
Rbt b h02
c S max
Q

16. Порядок расчета на прочность по наклонным сечениям:

Rsw Asw
, при этом S должно быть меньше Smax
S
2. Проверяем условие qsw 0.25 Rbt b Если условие не выполняется, то хомуты не
1. Определяем величину
qsw
учитываются и элемент рассчитывается как балка без арматуры.
M b 1.5 Rbt b h02
3. Определяем момент, воспринимаемый бетоном сжатой зоны
4. Определяем величину проекции опасного наклонного сечения:
а. При действии сосредоточенных сил определяем величину пролета среза:
с – равно расстоянию от опоры до точки приложения силы, но не больше
не больше 3∙ h0 и не менее h0;
Mb
0.75 qsw
M
b
Но если
б. При действии сплошной равномерно распределенной нагрузки c
q
Mb
2 h0
q
M
sw
b
или
2 , то c
не больше 3∙ h0 и не менее h0;
q1 1 0.5 qsw
Rbt b
q 0.75 qsw
Rbt b
5. Определяем величину проекции наклонной трещины с0=с, но не меньше h0 и не
больше 2 h0 .
6. Определяем величины
M b 1.5 Rbt b h02
Qb
c
c
и
Qsw 0.75 q sw c0
7. Проверяем условие: Q Qb Qsw если условие выполняется – прочность обеспечена.

17. Порядок подбора поперечной арматуры при действии равномерно распределенной нагрузки.

1. Проверяем необходимость установки поперечной арматуры из условия:
Qmax 0.5 Rbt b h0
2. Проверяем условие прочности по бетонной полосе между наклонными сечениями:
Q 0.3 Rb b h0
3. Вычисляем величину
если
2 Mb
Qb1
Qmax
h0
если Qb1
если
Qb1 2 M b q1
2 Mb
Qmax
h0
Qb1 Rbt b h0
2
Qmax
Qb21
тогда qsw
3 Mb
тогда qsw
тогда
Qmax Qb1
1.5 h0
qsw
Qmax 0.5 b h0 3 h0 q1
1.5 h0

18.

4. Проверяем условие
qsw 0.25 Rbt b
Если оно не выполняется, то пересчитываем требуемую арматуру по формуле:
2
Qmax
Qmax
8 q1
8 q1
2
h
h
Qmax
qsw 0
0
1.5 h0
1.5
1.5
но не менее
Qmax
3 q1
h0
3. 5
5. Задаемся шагом хомутов S. Проверяем максимально допустимый шаг хомутов по
конструктивным требованиям и по формуле:
Smax
Rbt b h02
Q
6. Определяем требуемую площадь хомутов:
Asw
qsw S
Rsw

19. Порядок подбора поперечной арматуры при действии сосредоточенных сил.

1. Проверяем необходимость установки поперечной арматуры из условия:
Qmax 0.5 Rbt b h0
2. Проверяем условие прочности по бетонной полосе между наклонными сечениями:
Q 0.3 Rb b h0
3. Задаемся начальной величиной поперечного армирования . Для этого вычисляем вели-
чину:
ci
h0
(принимая сi равным расстоянию от опоры до точки приложения силы).
Qi
1.5
0.187 0
При
i
zp
Rbt b h0
При
где
i zp
принимаем
qsw Rbt b
0 - меньшее из значений
принимаем
zp
qsw 0.25 Rbt b
1.5
0.75 0
и 2.
4. Проверяем прочность по поперечной силе и конструктивные требования, как указано
выше.

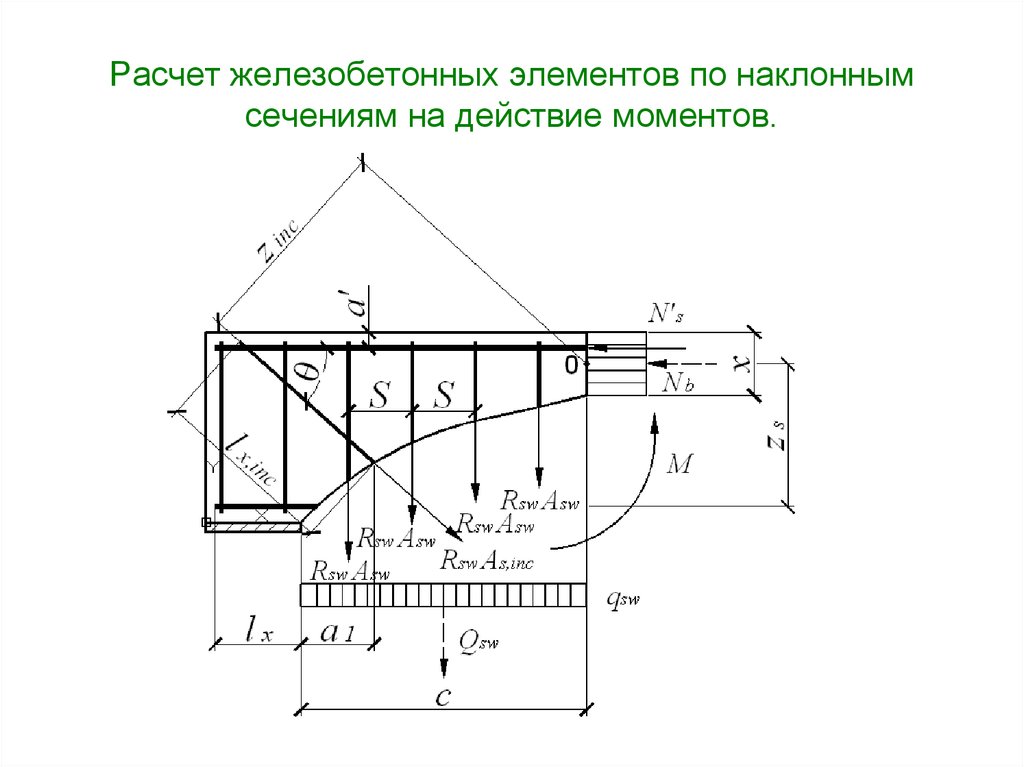
20. Расчет железобетонных элементов по наклонным сечениям на действие моментов.

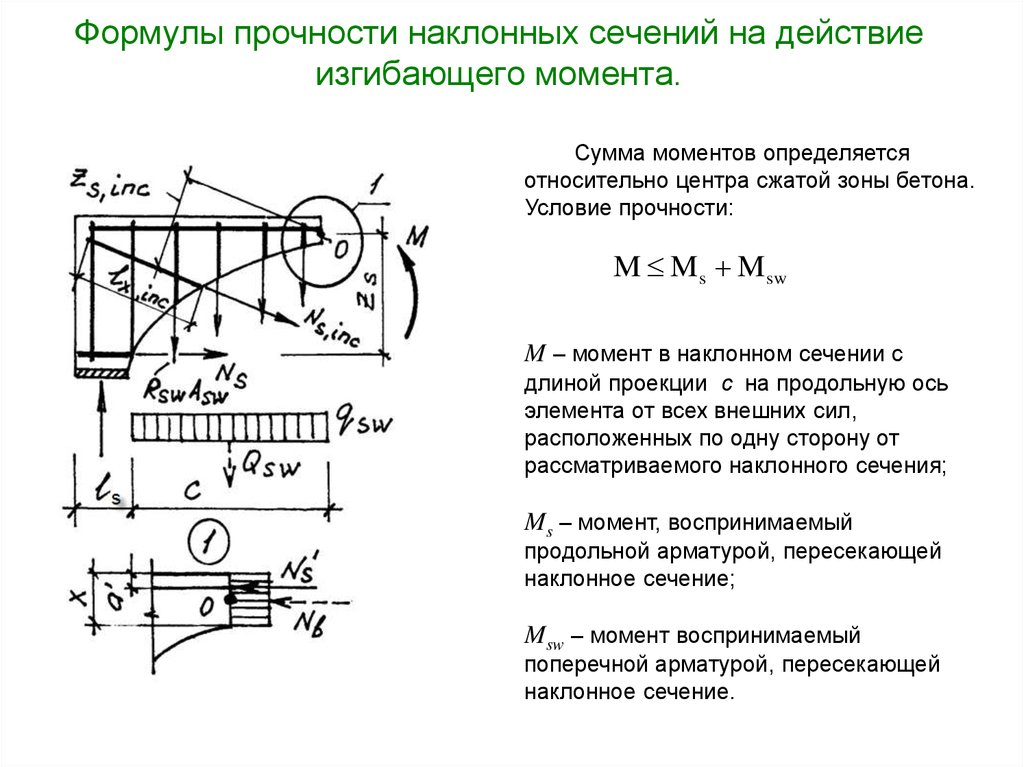
21. Формулы прочности наклонных сечений на действие изгибающего момента.

Сумма моментов определяется
относительно центра сжатой зоны бетона.
Условие прочности:
M Ms Msw
M – момент в наклонном сечении с
длиной проекции c на продольную ось
элемента от всех внешних сил,
расположенных по одну сторону от
рассматриваемого наклонного сечения;
Ms – момент, воспринимаемый
продольной арматурой, пересекающей
наклонное сечение;
Msw – момент воспринимаемый
поперечной арматурой, пересекающей
наклонное сечение.

22.

Ms Ns zs
Ns – усилие в продольной растянутой арматуре, при отсутствии анкеров в пределах
зоны анкеровки (т.е. если анкеровка не обеспечена) принимаемое равным:
Ns R s As
ls
l an
ls – расстояние от конца арматуры до точки пересечения с ней наклонного сечения;
lan – длина зоны анкеровки
Плечо внутренней пары сил zs определяется по формуле:
z s h0 0.5 x h0
Ns
2 Rb b
Можно определять zs по упрощенной формуле:
z s 0.9 h 0
M sw 0.5 q sw c 2

23. Определение проекции расчетного сечения.

1.
При расчете прочности на М наклонное сечение и наклонную трещину не
разделяют, а пользуются единой проекцией с.
2. Имеется ограничение: с 2ho.
3. Расчетное сечение определяется из условия минимума несущей способности по
изгибаемому моменту
d M u M
0
dc
а) Так как Ms = Ns zs = const, при действии равномерно распределенной нагрузки:
c
Qmax
q sw q
б) При действии сосредоточенной силы значение c принимается наименьшему из двух
величин: расстояния от опоры до точки приложения сосредоточенных сил или
Qmax
q sw

24.

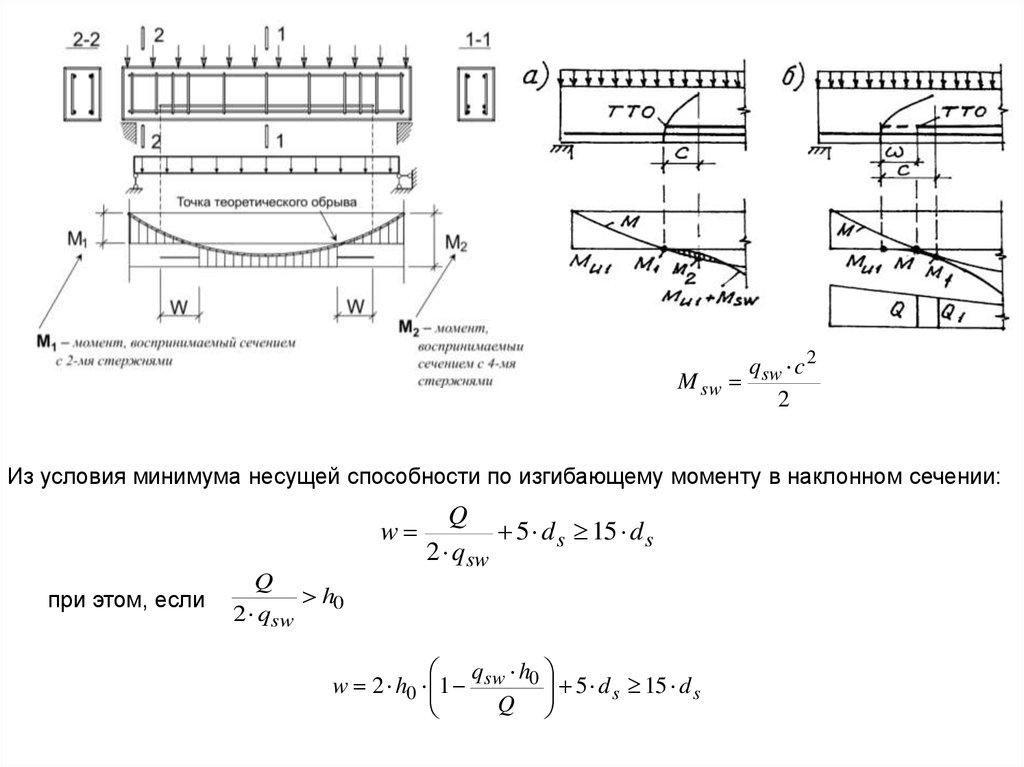
qsw c 2
M sw
2
Из условия минимума несущей способности по изгибающему моменту в наклонном сечении:
w
при этом, если
Q
5 d s 15 d s
2 qsw
Q
h0
2 qsw
q h
w 2 h0 1 sw 0 5 d s 15 d s
Q