Конструктивные особенности изгибаемых железобетонных элементов

1. Конструктивные особенности изгибаемых железобетонных элементов

Наиболее распространенные изгибаемые элементы –
плиты и балки.
1

2. Конструктивные особенности изгибаемых железобетонных элементов

Наиболее распространенные изгибаемые элементы –
плиты и балки.
Плиты – плоские элементы, толщина которых
значительно меньше длины и ширины.
Балки – линейные элементы, длина которых
значительно превышает поперечные размеры.
Плиты и балки могут быть однопролетными и
многопролетными.
2

3. Конструктивные особенности изгибаемых железобетонных элементов

Наиболее распространенные изгибаемые элементы – плиты и балки.
Плиты – плоские элементы, толщина которых значительно меньше длины и ширины.
Балки – линейные элементы, длина которых значительно превышает поперечные
размеры.
Плиты и балки могут быть однопролетными и многопролетными.
Плиты армируют сварными сетками.
Сетки укладывают так, чтобы стержни их рабочей
арматуры воспринимали растягивающие усилия,
возникающие при изгибе, в соответствии с эпюрами
изгибающих моментов.
3

4. Конструктивные особенности изгибаемых железобетонных элементов

Плиты армируют сварными сетками.
Сетки укладывают так, чтобы стержни их рабочей
арматуры воспринимали растягивающие усилия,
возникающие при изгибе, в соответствии с эпюрами
изгибающих моментов.
В плитах сетки размещаются понизу, а в
многопролетных
плитах
и
поверху,
над
промежуточных опорах.
4

5. Конструктивные особенности изгибаемых железобетонных элементов

Плиты армируют сварными сетками.
Сетки укладывают так, чтобы стержни их рабочей арматуры воспринимали
растягивающие усилия, возникающие при изгибе, в соответствии с эпюрами
изгибающих моментов.
В плитах сетки размещаются понизу, а в многопролетных плитах и поверху, над
промежуточных опорах.
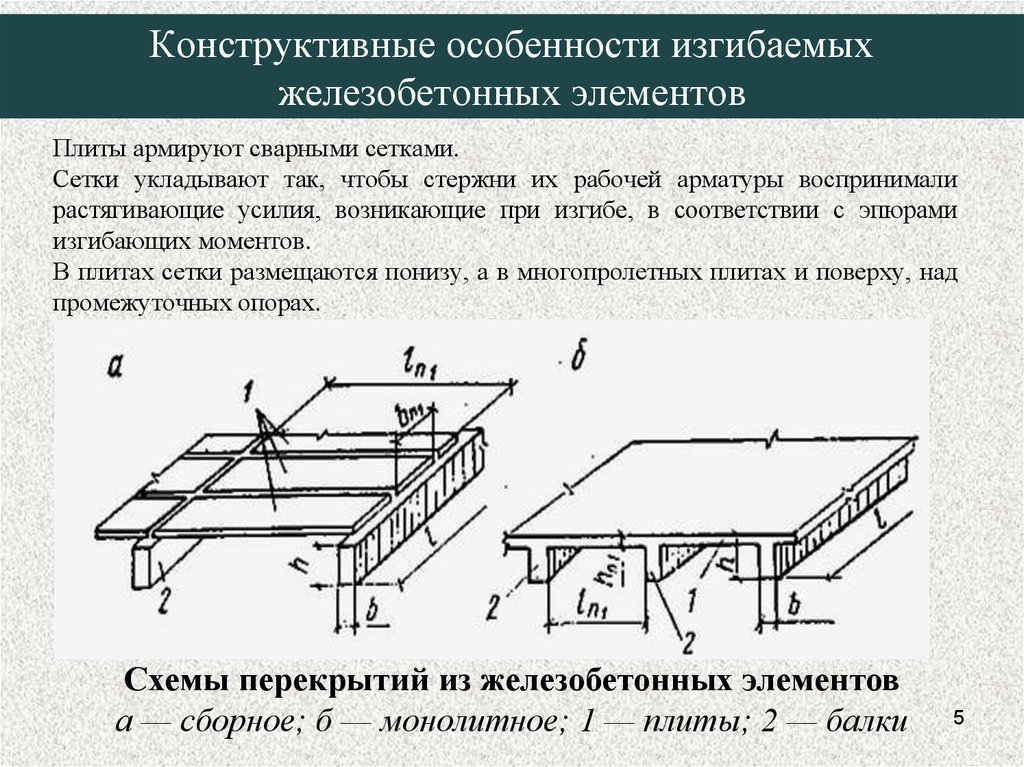
Схемы перекрытий из железобетонных элементов
а — сборное; б — монолитное; 1 — плиты; 2 — балки
5

6. Конструктивные особенности изгибаемых железобетонных элементов

Стержни рабочей арматуры принимают диаметром
3…10мм, с шагом 100…200мм. Защитный слой бетона
для рабочей арматуры принимают не менее диаметра и
не менее 10мм, а в толстых плитах (толще 100мм) не
менее 15 мм.
6

7. Конструктивные особенности изгибаемых железобетонных элементов

Стержни рабочей арматуры принимают диаметром 3…10мм, с шагом 100…200мм.
Защитный слой бетона для рабочей арматуры принимают не менее диаметра и не
менее 10мм, а в толстых плитах (толще 100мм) не менее 15 мм.
Поперечные стержни сеток (распределительная
арматура) устанавливают для обеспечения проектного
положения рабочих стержней, уменьшения усадочных
и
температурных
деформаций
конструкции,
распределения местного воздействия сосредоточенных
нагрузок.
7

8. Конструктивные особенности изгибаемых железобетонных элементов

Стержни рабочей арматуры принимают диаметром 3…10мм, с шагом 100…200мм.
Защитный слой бетона для рабочей арматуры принимают не менее диаметра и не
менее 10мм, а в толстых плитах (толще 100мм) не менее 15 мм.
Поперечные стержни сеток (распределительная арматура) устанавливают для
обеспечения проектного положения рабочих стержней, уменьшения усадочных и
температурных деформаций конструкции, распределения местного воздействия
сосредоточенных нагрузок.
Общее сечение поперечных стержней принимают не
менее 10% сечения рабочей арматуры.
Шаг поперечных стержней –250…350мм.
8

9. Конструктивные особенности изгибаемых железобетонных элементов

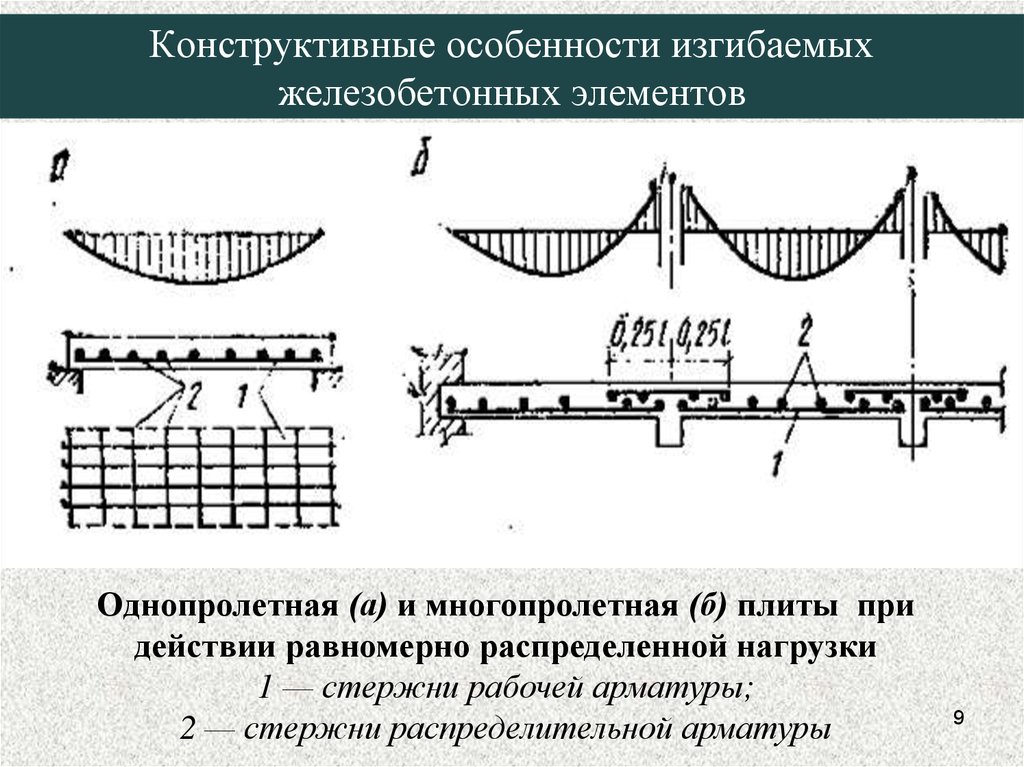
Однопролетная (а) и многопролетная (б) плиты при
действии равномерно распределенной нагрузки
1 — стержни рабочей арматуры;
2 — стержни распределительной арматуры
9

10. ЖЕЛЕЗОБЕТОННЫЕ БАЛКИ

Железобетонные балки могут быть сборными,
монолитными и сборно-монолитными, по форме
поперечного сечения – прямоугольного, таврового
двутаврового, трапециевидного и т. д.
10

11. ЖЕЛЕЗОБЕТОННЫЕ БАЛКИ

Железобетонные балки могут быть сборными, монолитными и сборномонолитными, по форме поперечного сечения – прямоугольного, таврового
двутаврового, трапециевидного и т. д.
Высота сечения балок может быть 1/10…1/20 от
пролета и назначается кратной 50мм, если она не
более 600мм, и кратной 100мм – при h>600мм и ≤
800мм, затем 1000мм и 1200мм и далее кратные
300мм.
11

12. ЖЕЛЕЗОБЕТОННЫЕ БАЛКИ

Железобетонные балки могут быть сборными, монолитными и сборномонолитными, по форме поперечного сечения – прямоугольного, таврового
двутаврового, трапециевидного и т. д.
Высота сечения балок может быть 1/10…1/20 от пролета и назначается кратной
50мм, если она не более 600мм, и кратной 100мм – при h>600мм и ≤ 800мм,
затем 1000мм и 1200мм и далее кратные 300мм.
Ширину
прямоугольных
сечений
принимают
b=(0,30…0,5)h. Ширина сечения балок зависит от
диаметра продольной арматуры и крупности
заполнителя. Рекомендуемая ширина сечения балок
b=100, 150, 200, 220, 250мм и далее кратно 50мм.
12

13. ЖЕЛЕЗОБЕТОННЫЕ БАЛКИ

Железобетонные балки могут быть сборными, монолитными и сборномонолитными, по форме поперечного сечения – прямоугольного, таврового
двутаврового, трапециевидного и т. д.
Высота сечения балок может быть 1/10…1/20 от пролета и назначается кратной
50мм, если она не более 600мм, и кратной 100мм – при h>600мм и ≤ 800мм,
затем 1000мм и 1200мм и далее кратные 300мм.
Ширину прямоугольных сечений принимают b=(0,30…0,5)h. Ширина сечения балок
зависит от диаметра продольной арматуры и крупности заполнителя. Рекомендуемая
ширина сечения балок b=100, 150, 200, 220, 250мм и далее кратно 50мм.
Число продольных рабочих гибких стержней,
заводимых за грань опоры балки, должно быть не
менее двух.
При ширине b≤150мм допускается установка одного
стержня.
13

14.

Поперечное сечение балок и схемы армирования
а — прямоугольное; б — тавровое; в — двутавровое; г — трапециевидное
1 — продольные стержни; 2 — поперечная арматура
14

15. ЖЕЛЕЗОБЕТОННЫЕ БАЛКИ

Расстояние в свету между стержнями продольной
арматуры, должно быть не менее наибольшего
диаметра стержней, при этом для нижних
горизонтальных (при бетонировании) - не менее 25мм,
а для верхних стержней – не менее 30мм.
15

16. ЖЕЛЕЗОБЕТОННЫЕ БАЛКИ

Расстояние в свету между стержнями продольной арматуры, должно быть не менее
наибольшего диаметра стержней, при этом для нижних горизонтальных (при
бетонировании) - не менее 25мм, а для верхних стержней – не менее 30мм.
При расположении нижней арматуры более чем в два
раза по высоте сечения расстояние между стержнями,
расположенными в третьем и следующих рядах,
должно быть не менее 50мм.
В стесненных условиях стержни можно располагать
попарно без зазоров.
16

17.

Размещение арматуры в поперечном сечении балок
al — защитный слой бетона для рабочей арматуры; aw — то же для поперечной
арматуры; d — наибольший диаметр рабочих стержней; a1 — расстояние в свету
между нижними (при бетонировании) продольными стержнями; a/1 — то же, между
верхними (при бетонировании) стержнями; a2 — расстояние в свету между рядами
продольных стержней
17

18.

Размещение арматуры в поперечном сечении балок
Продольную рабочую арматуру в балках (и плитах)
укладывают согласно эпюрам изгибающих моментов в
растянутых зонах.
Для экономии стали часть продольных арматурных
стержней можно не доводить до опор и обрывать в
пролете в месте, где они по расчету на восприятие
изгибающего момента не требуется.
18

19.

Размещение арматуры в поперечном сечении балок
Продольную рабочую арматуру в балках (и плитах) укладывают согласно эпюрам
изгибающих моментов в растянутых зонах.
Для экономии стали часть продольных арматурных стержней можно не доводить до
опор и обрывать в пролете в месте, где они по расчету на восприятие изгибающего
момента не требуется.
Диаметр стержней рабочей арматуры балок d≥10мм.
Желательно
назначать
все
рабочие
стержни
одинакового диаметра и не более 32мм.
При назначении рабочей арматуры для элементов из
легкого бетона предпочтение рекомендуется отдавать
мелким диаметрам (d≤18мм).
19

20.

Размещение арматуры в поперечном сечении балок
При высоте сечения более
700мм у боковых граней
должны ставиться монтажные
продольные
стержни
с
площадью сечения не менее
0,1% от площади Аb1.
20

21.

Схемы армирования балок сварными каркасами (а) и
вязаной арматурой (б)
1 — продольные рабочие стержни (стержни второго ряда не доведены до
опор); 2 — поперечные стержни каркасов; 3 — продольные монтажные
стержни; 4 — поперечные соединительные стержни; 5 — рабочие стержни
с отгибами; 6 — хомуты вязаных каркасов
21

22.

Размещение арматуры в поперечном сечении балок
Продольную и поперечную арматуру объединяют в
сварные или вязаные каркасы.
Вязаные каркасы весьма трудоемки и применяются в
случаях, если изготовление сварных каркасов
невозможно.
22

23.

Размещение арматуры в поперечном сечении балок
Продольную и поперечную арматуру объединяют в сварные или вязаные каркасы.
Вязаные каркасы весьма трудоемки и применяются в случаях, если изготовление
сварных каркасов невозможно.
Плоские
сварные
каркасы
объединяют
в
пространственные
с
помощью
горизонтальных
поперечных стержней, устанавливаемых через 1…1,5 м.
При армировании вязаными каркасами хомуты в балках
прямоугольного сечения делают замкнутыми.
23

24.

Размещение арматуры в поперечном сечении балок
Продольную и поперечную арматуру объединяют в сварные или вязаные каркасы.
Вязаные каркасы весьма трудоемки и применяются в случаях, если изготовление
сварных каркасов невозможно.
Плоские сварные каркасы объединяют в пространственные с помощью горизонтальных
поперечных стержней, устанавливаемых через 1…1,5 м.
При армировании вязаными каркасами хомуты в балках прямоугольного сечения
делают замкнутыми.
В балках шириной более 350мм устанавливают
многоветвевые хомуты.
Диаметр хомутов вязаных каркасов принимают не
менее 6 мм при высоте балок до 800мм и не менее
8 мм при большей высоте.
24

25.

Размещение арматуры в поперечном сечении балок
Продольную и поперечную арматуру объединяют в сварные или вязаные каркасы.
Вязаные каркасы весьма трудоемки и применяются в случаях, если изготовление
сварных каркасов невозможно.
Плоские сварные каркасы объединяют в пространственные с помощью горизонтальных
поперечных стержней, устанавливаемых через 1…1,5 м.
При армировании вязаными каркасами хомуты в балках прямоугольного сечения
делают замкнутыми.
В балках шириной более 350мм устанавливают многоветвевые хомуты.
Диаметр хомутов вязаных каркасов принимают не менее 6 мм при высоте балок до
800мм и не менее 8 мм при большей высоте.
Поперечную арматуру следует устанавливать исходя из
расчета на восприятие усилий, а также с целью
ограничения развития трещин, удержания продольных
стержней в проектном положении и закрепления их от
бокового выпучивания в любом направлении.
25

26.

Размещение арматуры в поперечном сечении балок
Плоские сварные каркасы объединяют в пространственные с помощью горизонтальных
поперечных стержней, устанавливаемых через 1…1,5 м.
При армировании вязаными каркасами хомуты в балках прямоугольного сечения
делают замкнутыми.
В балках шириной более 350мм устанавливают многоветвевые хомуты.
Диаметр хомутов вязаных каркасов принимают не менее 6 мм при высоте балок до
800мм и не менее 8 мм при большей высоте.
Поперечную арматуру следует устанавливать исходя из расчета на восприятие усилий,
а также с целью ограничения развития трещин, удержания продольных стержней в
проектном положении и закрепления их от бокового выпучивания в любом
направлении.
Поперечную арматуру устанавливают у всех
поверхностей железобетонных элементов, вблизи
которых ставится продольная арматура.
При этом расстояния между поперечными стержнями у
каждой поверхности элемента должны быть не более
600 мм и не более удвоенной ширины грани элемента.26

27.

Размещение арматуры в поперечном сечении балок
В балках шириной более 350мм устанавливают многоветвевые хомуты.
Диаметр хомутов вязаных каркасов принимают не менее 6 мм при высоте балок до
800мм и не менее 8 мм при большей высоте.
Поперечную арматуру следует устанавливать исходя из расчета на восприятие усилий,
а также с целью ограничения развития трещин, удержания продольных стержней в
проектном положении и закрепления их от бокового выпучивания в любом
направлении.
Поперечную арматуру устанавливают у всех поверхностей железобетонных элементов,
вблизи которых ставится продольная арматура.
При этом расстояния между поперечными стержнями у каждой поверхности элемента
должны быть не более 600 мм и не более удвоенной ширины грани элемента.
Шаг и диаметр поперечной арматуры в балках
устанавливается по расчету на действие поперечной
силы. Диаметр поперечной арматуры в вязаных
каркасах изгибаемых элементов принимают не менее
6 мм.
27

28.

Размещение арматуры в поперечном сечении балок
При этом по конструктивным условиям на приопорных
участках балок длиной ¼ пролета при равномерно
распределенной
нагрузке
расстояние
между
поперечными стержнями (или хомутами) в элементах
без отгибов должно быть:
• В железобетонных элементах, в которых поперечная
сила по расчету не может быть воспринята только
бетоном,
следует
предусматривать
установку
поперечной арматуры с шагом не более 0,5h0 и не
более 300 мм.
28

29.

Размещение арматуры в поперечном сечении балок
При этом по конструктивным условиям на приопорных участках балок длиной ¼
пролета при равномерно распределенной нагрузке расстояние между поперечными
стержнями (или хомутами) в элементах без отгибов должно быть:
• В железобетонных элементах, в которых поперечная сила по расчету не может быть
воспринята только бетоном, следует предусматривать установку поперечной
арматуры с шагом не более 0,5h0 и не более 300 мм.
• В сплошных плитах, а также в многопустотных и
часторебристых плитах высотой менее 300 мм и в
балках (ребрах) высотой менее 150 мм на участке
элемента, где поперечная сила по расчету
воспринимается только бетоном, поперечную арматуру
можно не устанавливать.
29

30.

Размещение арматуры в поперечном сечении балок
При этом по конструктивным условиям на приопорных участках балок длиной ¼
пролета при равномерно распределенной нагрузке расстояние между поперечными
стержнями (или хомутами) в элементах без отгибов должно быть:
• В железобетонных элементах, в которых поперечная сила по расчету не может быть
воспринята только бетоном, следует предусматривать установку поперечной
арматуры с шагом не более 0,5h0 и не более 300 мм.
• В сплошных плитах, а также в многопустотных и часторебристых плитах высотой
менее 300 мм и в балках (ребрах) высотой менее 150 мм на участке элемента, где
поперечная сила по расчету воспринимается только бетоном, поперечную арматуру
можно не устанавливать.
• В балках и ребрах высотой 150 мм и более, а также в
часторебристых плитах высотой 300 мм и более на
участках элемента, где поперечная сила по расчету
воспринимается
только
бетоном,
следует
предусматривать установку поперечной арматуры с
шагом не более 0,75h0 и не более 500 мм.
30

31.

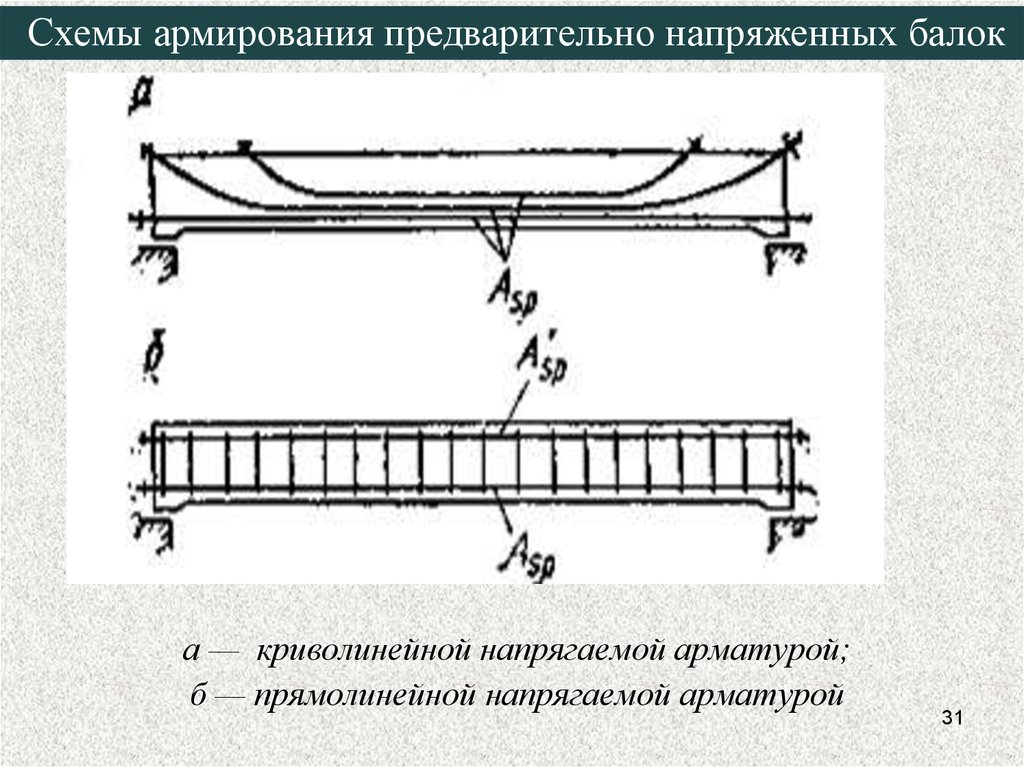
Схемы армирования предварительно напряженных балок
а — криволинейной напрягаемой арматурой;
б — прямолинейной напрягаемой арматурой
31

32.

Примеры армирования растянутой зоны балки
32

33.

Схемы местного усиления концевых участков
предварительно напряженных балок
а — поперечными сварными сетками;
б — хомутами или сварной сеткой в обхват
33

34. Расчет по нормальному сечению изгибаемых железобетонных элементов прямоугольного профиля без предварительного напряжения с

одиночным армированием
Железобетонными
элементами
с
одиночным
армированием называются такие элементы, у которых
расчетная продольная рабочая арматура расположена
у растянутой грани.
34

35. Расчет по нормальному сечению изгибаемых железобетонных элементов прямоугольного профиля без предварительного напряжения с

одиночным армированием
Железобетонными элементами с одиночным армированием называются такие
элементы, у которых расчетная продольная рабочая арматура расположена у
растянутой грани.
Расчет
прочности
по
нормальным
сечениям
изгибаемых железобетонных элементов ведется по III
стадии напряженно-деформированного состояния
(стадии разрушения).
Возможны два случая разрушения изгибаемых
элементов по нормальным сечениям.
35

36. Расчет по нормальному сечению изгибаемых железобетонных элементов прямоугольного профиля без предварительного напряжения с

одиночным армированием
Первый вариант разрушения носит пластический
характер
Разрушение элемента начинается при достижении в
растянутой арматуре физического или условного
предела текучести.
Появляются и раскрываются трещины в бетоне
растянутой зоны, после чего происходит дробление
сжатой зоны бетона.
36

37. Расчет по нормальному сечению изгибаемых железобетонных элементов прямоугольного профиля без предварительного напряжения с

одиночным армированием
Первый вариант разрушения носит пластический
характер
Разрушение элемента начинается при достижении в
растянутой арматуре физического или условного
предела текучести.
Появляются и раскрываются трещины в бетоне
растянутой зоны, после чего происходит дробление
сжатой зоны бетона.
Процесс разрушения протекает плавно.
Прочностные
характеристики
арматуры
используются полностью.
37

38. Расчет по нормальному сечению изгибаемых железобетонных элементов прямоугольного профиля без предварительного напряжения с

одиночным армированием
При втором варианте разрушение носит хрупкий,
катастрофический
характер
и
начинается
дроблением бетона сжатой зоны
Трещины в бетоне растянутой зоны либо не
образуются, либо ширина их раскрытия в момент
разрушения не превышает предельно допустимой.
38

39. Расчет по нормальному сечению изгибаемых железобетонных элементов прямоугольного профиля без предварительного напряжения с

одиночным армированием
При втором варианте разрушение носит хрупкий,
катастрофический
характер
и
начинается
дроблением бетона сжатой зоны
Трещины в бетоне растянутой зоны либо не
образуются, либо ширина их раскрытия в момент
разрушения не превышает предельно допустимой.
Напряжения в растянутой арматуре не достигают
физического или условного предела текучести,
следовательно, прочностные свойства арматуры
используются не полностью.
39

40. Расчет по нормальному сечению изгибаемых железобетонных элементов прямоугольного профиля без предварительного напряжения с

одиночным армированием
Характер разрушения определяется величиной
относительной высоты сжатой зоны, которая зависит
от коэффициента армирования, класса бетона и
арматуры.
40

41.

Основные предпосылки и допущения расчета по
нормальным сечениям изгибаемых
железобетонных элементов
• предельное состояние наступает в случае, если
сжатый бетон или растянутая арматура достигает
своего предельного состояния;
41

42.

Основные предпосылки и допущения расчета по
нормальным сечениям изгибаемых
железобетонных элементов
• предельное состояние наступает в случае, если сжатый бетон или растянутая
арматура достигает своего предельного состояния;
• разрушение элемента определяется в большинстве
случаев разрушением бетона в сжатой зоне;
42

43.

Основные предпосылки и допущения расчета по
нормальным сечениям изгибаемых
железобетонных элементов
• предельное состояние наступает в случае, если сжатый бетон или растянутая
арматура достигает своего предельного состояния;
• разрушение элемента определяется в большинстве случаев разрушением бетона в
сжатой зоне;
• расчет элементов производится из условия
равновесия внешних сил и предельных внутренних
усилий;
43

44.

Основные предпосылки и допущения расчета по
нормальным сечениям изгибаемых
железобетонных элементов
• предельное состояние наступает в случае, если сжатый бетон или растянутая
арматура достигает своего предельного состояния;
• разрушение элемента определяется в большинстве случаев разрушением бетона в
сжатой зоне;
• расчет элементов производится из условия равновесия внешних сил и предельных
внутренних усилий;
• сопротивление
равным нулю;
бетона
растяжению
принимается
44

45.

Основные предпосылки и допущения расчета по
нормальным сечениям изгибаемых
железобетонных элементов
• предельное состояние наступает в случае, если сжатый бетон или растянутая
арматура достигает своего предельного состояния;
• разрушение элемента определяется в большинстве случаев разрушением бетона в
сжатой зоне;
• расчет элементов производится из условия равновесия внешних сил и предельных
внутренних усилий;
• сопротивление бетона растяжению принимается равным нулю;
• бетон в сжатой зоне представляет собою жесткопластический материал;
• напряжения в бетоне сжатой зоны равномерно
распределены по высоте сечения расчетной сжатой
зоны и равны призменной прочности бетона расчетному сопротивлению бетона осевому сжатию
для предельных состояний I группы;
45

46.

Основные предпосылки и допущения расчета по
нормальным сечениям изгибаемых
железобетонных элементов
• предельное состояние наступает в случае, если сжатый бетон или растянутая
арматура достигает своего предельного состояния;
• разрушение элемента определяется в большинстве случаев разрушением бетона в
сжатой зоне;
• расчет элементов производится из условия равновесия внешних сил и предельных
внутренних усилий;
• сопротивление бетона растяжению принимается равным нулю;
• бетон в сжатой зоне представляет собою жесткопластический материал;
• напряжения в бетоне сжатой зоны равномерно распределены по высоте сечения
расчетной сжатой зоны и равны призменной прочности бетона - расчетному
сопротивлению бетона осевому сжатию для предельных состояний I группы;
• растягивающие напряжения в арматуре достигают расчетного сопротивления
осевому растяжению, если высота условной сжатой зоны бетона не превосходит
граничную высоту сжатой зоны бетона;
• справедлива гипотеза плоских сечений (сечение,
плоское до изгиба, остается плоским после изгиба)
(малость сдвига по сравнению с углами поворота);
46

47.

Основные предпосылки и допущения расчета по
нормальным сечениям изгибаемых
железобетонных элементов
• предельное состояние наступает в случае, если сжатый бетон или растянутая
арматура достигает своего предельного состояния;
• разрушение элемента определяется в большинстве случаев разрушением бетона в
сжатой зоне;
• расчет элементов производится из условия равновесия внешних сил и предельных
внутренних усилий;
• сопротивление бетона растяжению принимается равным нулю;
• бетон в сжатой зоне представляет собою жесткопластический материал;
• напряжения в бетоне сжатой зоны равномерно распределены по высоте сечения
расчетной сжатой зоны и равны призменной прочности бетона - расчетному
сопротивлению бетона осевому сжатию для предельных состояний I группы;
• растягивающие напряжения в арматуре достигают расчетного сопротивления
осевому растяжению, если высота условной сжатой зоны бетона не превосходит
граничную высоту сжатой зоны бетона;
• справедлива гипотеза плоских сечений (сечение,
плоское до изгиба, остается плоским после изгиба)
(малость сдвига по сравнению с углами поворота);
1
1
bi zbxi ; si z sxi ;
rx
rx
47

48.

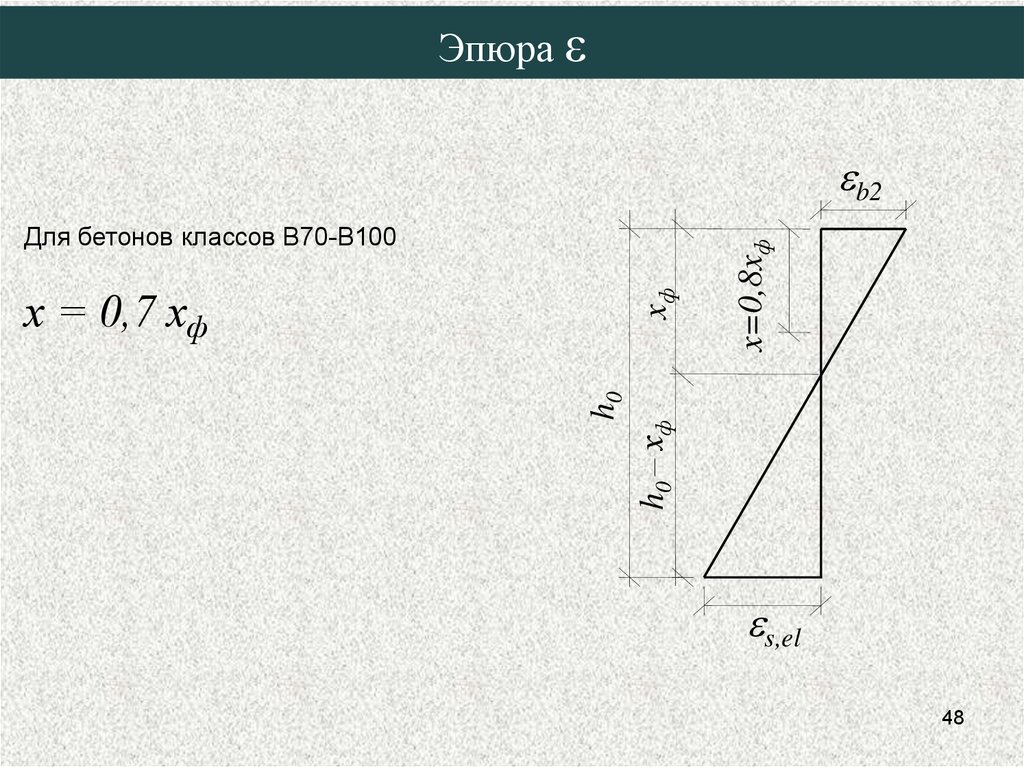
Эпюра ε
Для бетонов классов В70-В100
h0 – хф
h0
xф
х = 0,7 хф
x=0,8xф
b2
s,el
48

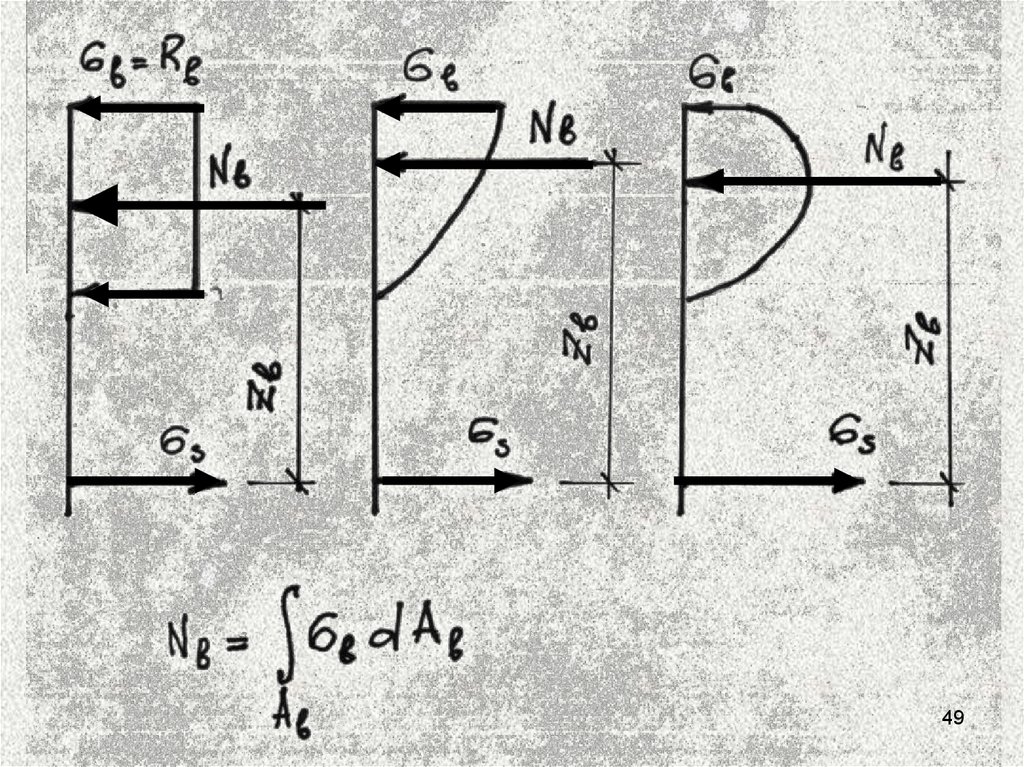
49.

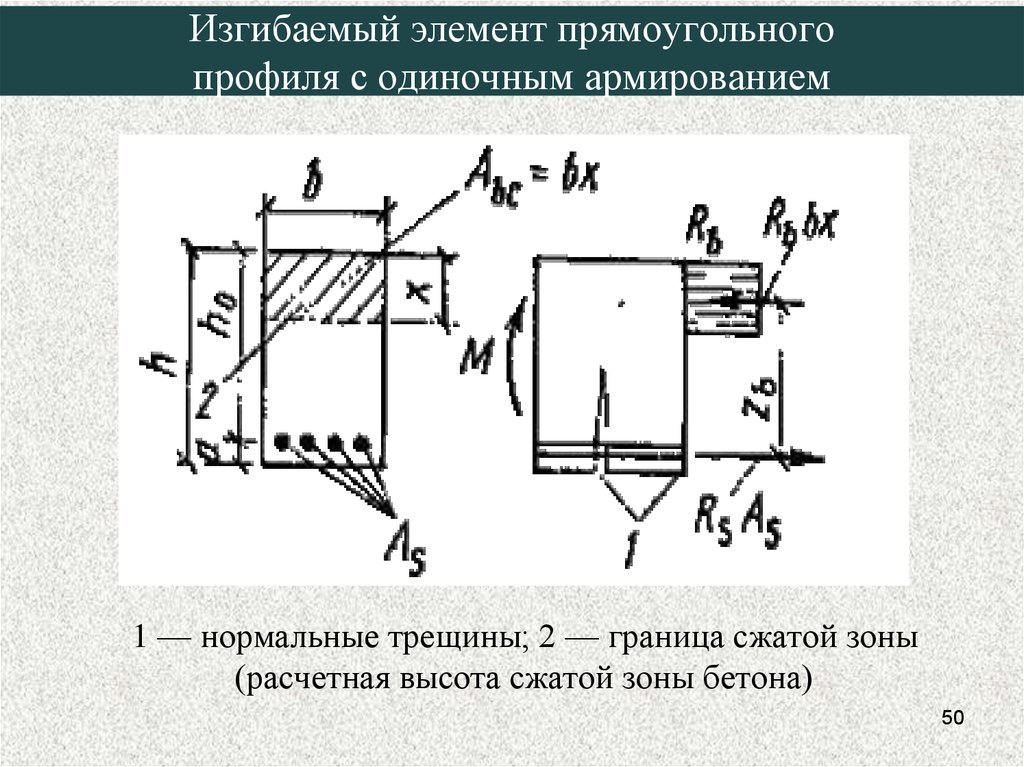
49

50. Изгибаемый элемент прямоугольного профиля с одиночным армированием

1 — нормальные трещины; 2 — граница сжатой зоны
(расчетная высота сжатой зоны бетона)
50

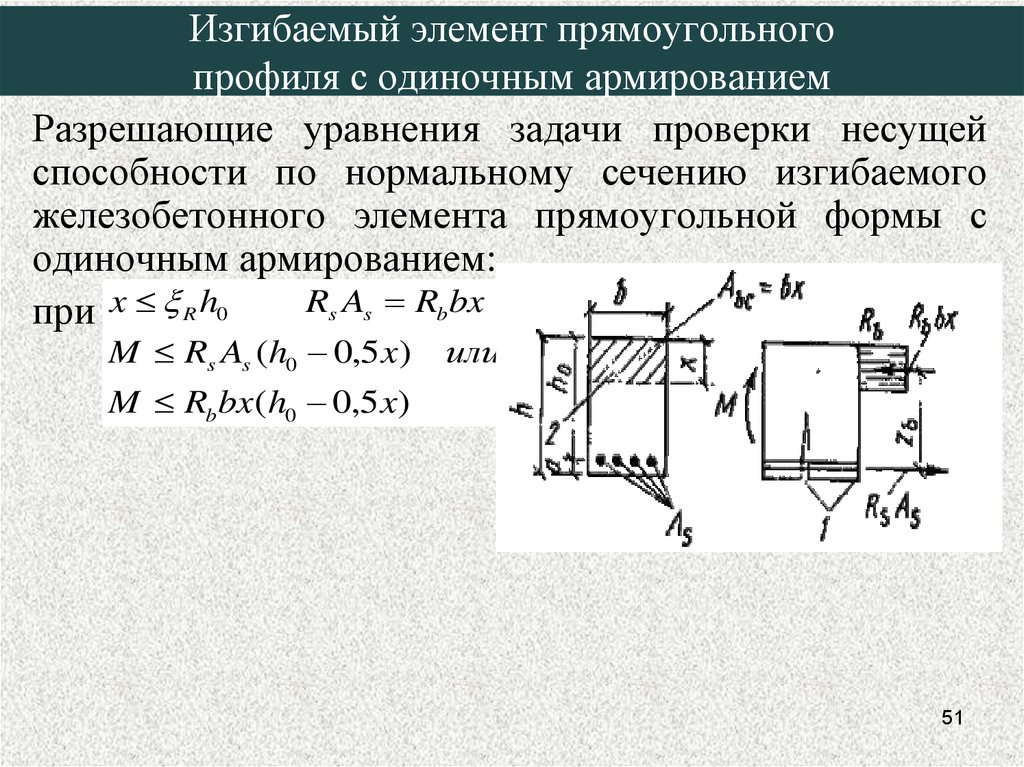
51. Изгибаемый элемент прямоугольного профиля с одиночным армированием

Разрешающие уравнения задачи проверки несущей
способности по нормальному сечению изгибаемого
железобетонного элемента прямоугольной формы с
одиночным армированием:
Rs As Rb bx
при x R h0
M Rs As (h0 0,5 x)
или
M Rb bx(h0 0,5 x)
51

52. Изгибаемый элемент прямоугольного профиля с одиночным армированием

Разрешающие уравнения задачи проверки несущей способности по нормальному
сечению изгибаемого железобетонного элемента прямоугольной формы с одиночным
армированием:
при x h
R A R bx
R 0
s
s
b
M Rs As (h0 0,5 x) или
M Rbbx(h0 0,5 x)
При расчете изгибаемых железобетонных конструкций
должно выполняться условие:
x ≤ xR
Выполнение
этого
условия
соответствует
пластическому характеру разрушения.
52

53. Изгибаемый элемент прямоугольного профиля с одиночным армированием

Разрешающие уравнения задачи проверки несущей способности по нормальному
сечению изгибаемого железобетонного элемента прямоугольной формы с одиночным
армированием:
при
x h
R A R bx
R 0
s
s
b
M Rs As (h0 0,5 x) или
M Rbbx(h0 0,5 x)
При расчете изгибаемых железобетонных конструкций должно выполняться условие:
x ≤ xR
Выполнение этого условия соответствует пластическому характеру разрушения.
Если x ≥ xR , разрушение будет иметь хрупкий
характер.
53

54. Изгибаемый элемент прямоугольного профиля с одиночным армированием

Разрешающие уравнения задачи проверки несущей способности по нормальному
сечению изгибаемого железобетонного элемента прямоугольной формы с одиночным
армированием:
при
x R h0
Rs As Rbbx
M Rs As (h0 0,5 x) или
M Rbbx(h0 0,5 x)
При расчете изгибаемых железобетонных конструкций должно выполняться условие:
x ≤ xR
Выполнение этого условия соответствует пластическому характеру разрушения.
Если x ≥ xR , разрушение будет иметь хрупкий
характер.
Невыполнение этого условия допускается только в
случае, если площадь сечения продольной растянутой
арматуры определена из расчета элемента по II группе
предельных состояний или по конструктивным
54
соображениям.

55. Изгибаемый элемент прямоугольного профиля с одиночным армированием

В этом случае, в качестве второго разрешающего
уравнения допускается использовать выражение:
M Rbbh02 R , R R 1 0,5 R ,
или
где :
M Rbbh02 0,7 R 0,3 m ,
m 1 0,5
55

56.

Изгибаемый элемент прямоугольного
профиля с двойным армированием
56

57.

Изгибаемый элемент прямоугольного
профиля с двойным армированием
Разрешающие уравнения задачи проверки несущей способности по нормальному
сечению изгибаемого железобетонного элемента прямоугольной формы с двойным
армированием:
x R h0
Rs As Rbbx Rsc As/
M Rs As (h0 0,5 x) Rsc A (0,5 x a )
/
s
/
или
M Rbbx(h0 0,5 x) Rsc As/ (h0 a / )
57

58.

Изгибаемый элемент прямоугольного
профиля с двойным армированием
Разрешающие уравнения задачи проверки несущей способности по нормальному
сечению изгибаемого железобетонного элемента прямоугольной формы с двойным
армированием: x h
R A R bx R A/
R 0
s
s
b
sc
s
M Rs As (h0 0,5 x) Rsc As/ (0,5 x a / )
или M Rbbx(h0 0,5 x) Rsc As/ (h0 a / )
В этом случае, в качестве второго разрешающего
уравнения допускается использовать выражение:
M Rbbh02 R Rsc As/ h0 a / ,
R R 1 0,5 R ,
или
M Rbbh02 0,7 R 0,3 m Rsc As/ h0 a / ,
где : m 1 0,5
58

59. Граничная относительная высота сжатой зоны бетона (СНиП 52-01-2003 АР)

;
Для бетонов классов В70-В100
x=0,8xф
Rs
; b 2 0,0035
Es
xф
s ,el
b2
h0-xф
где :
s ,el
1
b2
h0
R
0,8
х = 0,7 хф
s,el
59

60. Вывод формулы ξR (СП 52-101-2003)

xф
b ,ult
s ,el
x
xФ
, x 0,8 xФ ,
;
0,8
xФ
h0 xФ
x=0,8xф
b2
xR
0,8 h0
s ,el
1
b ,ult
h0
s ,el
1
b ,ult
xR
; R
h0
;
h0-xф
h0
xФ
b ,ult s ,el
h0
xФ s ,el xФ b ,ult h0 b ,ult ;
0,8
s ,el Es
1
b ,ult Es
0,8
,
Rs
1
700
s,el
где : b ,ult 3,5 10 3 ; Rs s ,el Es
60

61.

где :
sR
s ,cu
sR
1
1,1
Rs
Rs ; s
;
Es
0,008 Rb ;
0,85 для тяжелого бетона;
s ,cu 400 МПа при b 2 1,0;
xф
1
;
h0-xф
R
h0
b2
x=ω xф
Граничная относительная высота
сжатой зоны бетона (СНиП 2.03.01-84*)
s,el
s ,cu 500 МПа при b 2 0,9
b2
s ,cu
E s 1
1,1
61

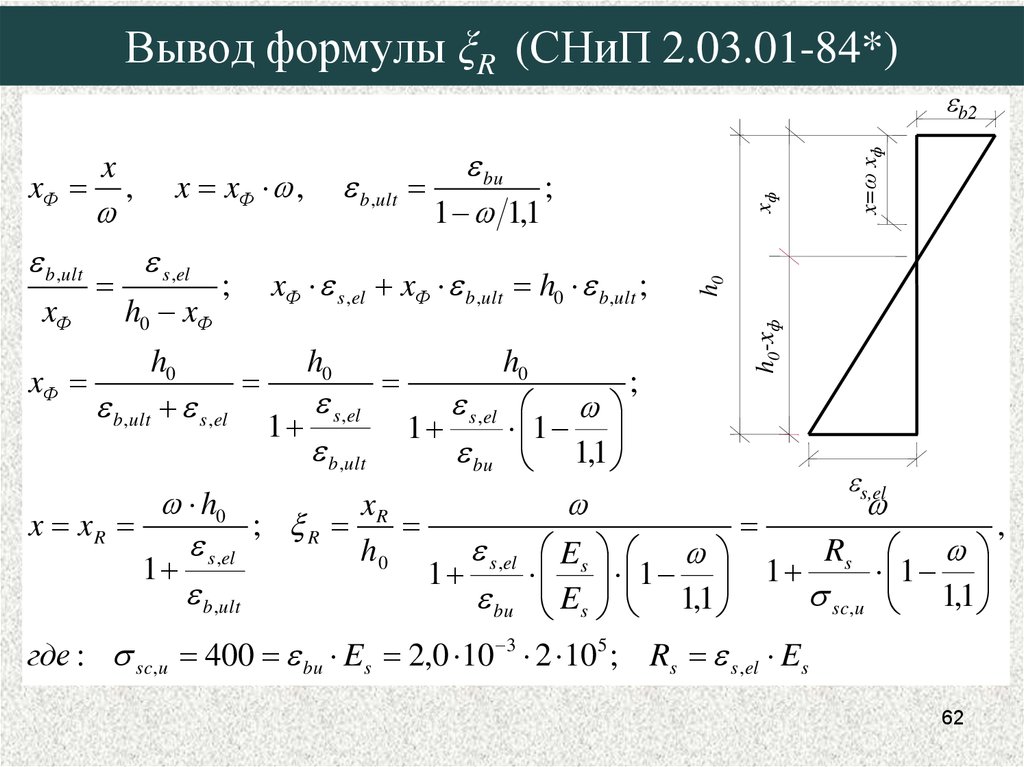
62. Вывод формулы ξR (СНиП 2.03.01-84*)

xФ
xФ
s ,el
h0 xФ
;
h0
b ,ult s ,el
b ,ult
bu
;
1 1,1
xФ s ,el xФ b ,ult h0 b ,ult ;
h0
s ,el
1
b ,ult
h0
;
s ,el
1
1
bu 1,1
h0
xR
x xR
; R
s ,el
s ,el
h0
1
1
b ,ult
bu
где : sc,u
xф
x xФ ,
,
h0-xф
b ,ult
x
h0
xФ
x=ω xф
b2
s,el
Rs
Es
1
1 1
sc,u 1,1
Es 1,1
400 bu Es 2,0 10 3 2 105 ; Rs s ,el Es
62
,

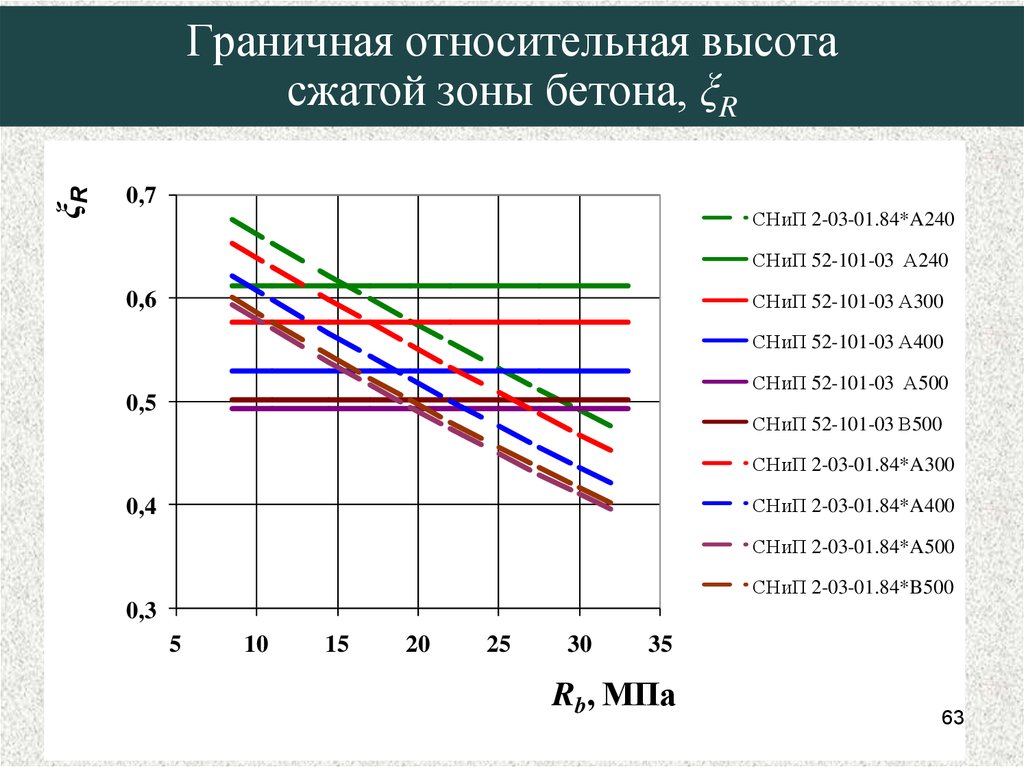
63. Граничная относительная высота сжатой зоны бетона, ξR

ξR
Граничная относительная высота
сжатой зоны бетона, ξR
0,7
СНиП 2-03-01.84*A240
СНиП 52-101-03 А240
СНиП 52-101-03 А300
0,6
СНиП 52-101-03 А400
СНиП 52-101-03 А500
0,5
СНиП 52-101-03 В500
СНиП 2-03-01.84*A300
СНиП 2-03-01.84*A400
0,4
СНиП 2-03-01.84*A500
СНиП 2-03-01.84*B500
0,3
5
10
15
20
25
30
35
Rb, МПа
63

64. График зависимости σ–ξ

Напряжения,МПа
250
0,557
200
sc,u
s
150
1
100
50
0,579 0,601
0,622
0,654 0,677
1
1,1
0,674
0,694
0,714
0,734
0,762
0,782
0
-50 0,0
0,2
0,4
0,6
0,7620,8
1,0
-100
-150
0,851
-200
0,866
0,880 0,894
0,913
0,930
-250
Относительная высота сжатой зоны бетона, ξ
В15
B20
B25
B30
B35
B40
64

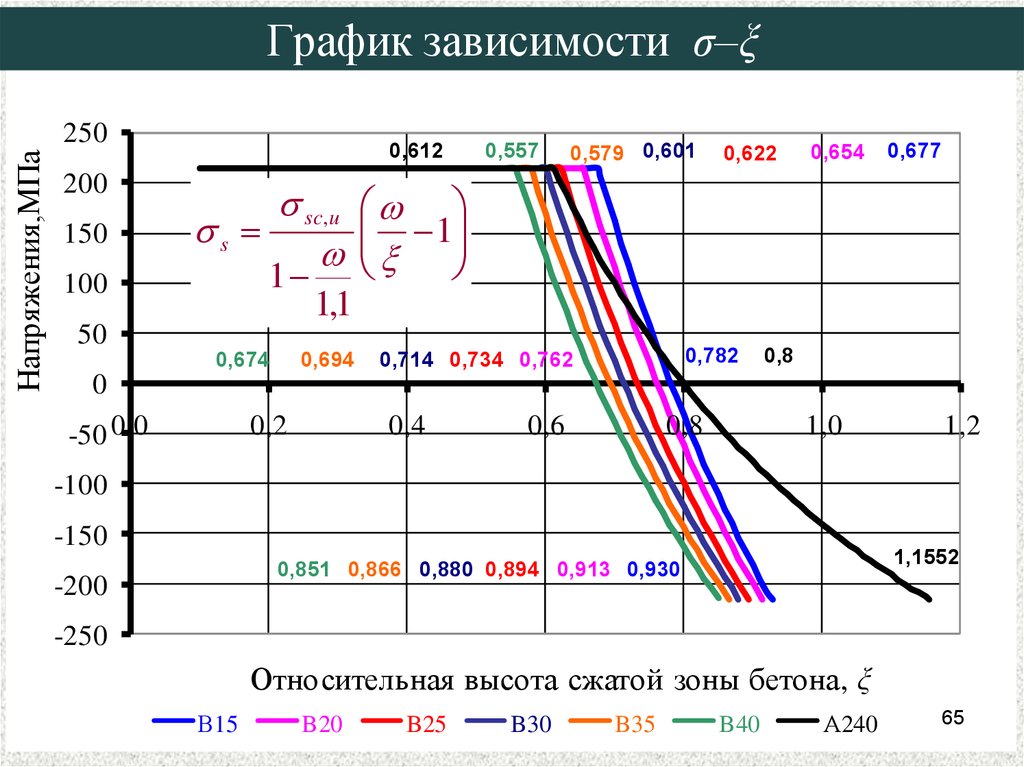
65. График зависимости σ–ξ

Напряжения,МПа
250
200
150
0,612
sc,u
s
1
100
0,557
0,579 0,601
0,654
0,677
1
1,1
50
0,674
0,622
0,694
0,782
0,714 0,734 0,762
0,8
0
-50 0,0
0,2
0,4
0,6
0,8
1,0
1,2
-100
-150
1,1552
0,851 0,866 0,880 0,894 0,913 0,930
-200
-250
Относительная высота сжатой зоны бетона, ξ
В15
B20
B25
B30
B35
B40
А240
65

66. График зависимости σ–ξ

Напряжения,МПа
400
0,502
200
sc,u
s
100
1,1
300
0
-100
1
0,674
0,0
0,694
0,714
0,2
0,523
0,599
0,544 0,567
0,622
1
0,734 0,762
0,782
0,4
0,6
0,8
1,0
1,2
-200
1,027 1,032
-300
1,037
1,042
1,048
1,052
-400
Относительная высота сжатой зоны бетона, ξ
В15
B20
B25
B30
B35
B40
66

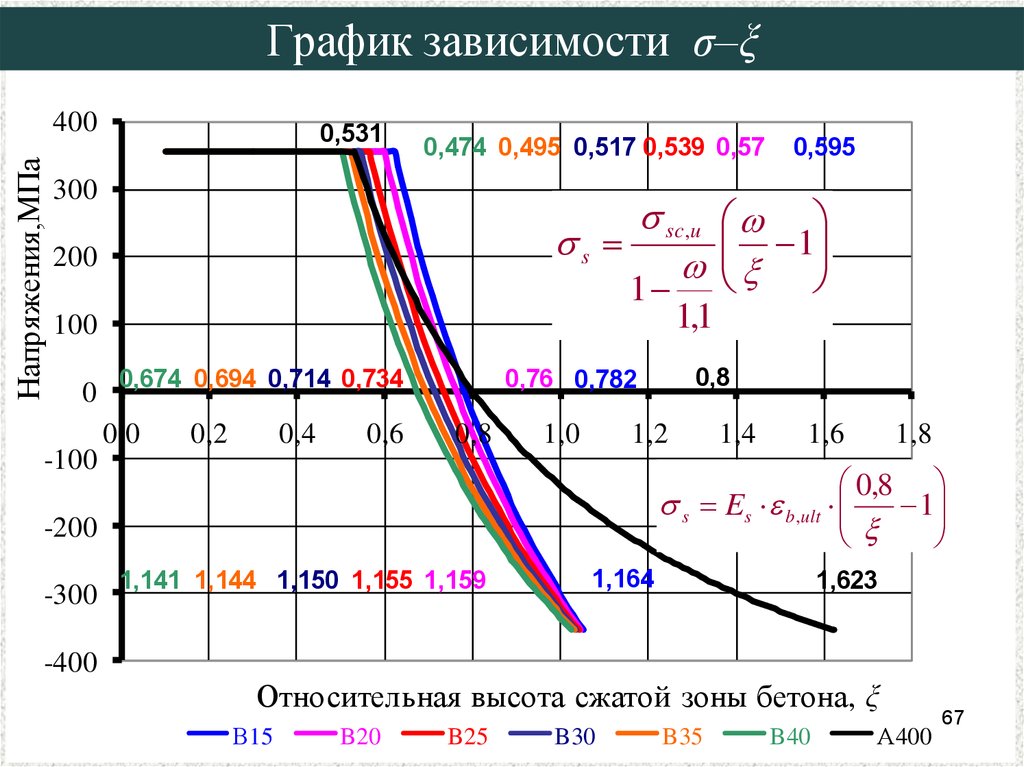
67. График зависимости σ–ξ

Напряжения,МПа
400
0,531
0,474 0,495 0,517 0,539 0,57
300
200
sc,u
s
100
1,1
1
0 0,674 0,694 0,714 0,734
0,0
0,2
0,4
0,6
-100
1,0
1,2
1,4
1,6
1,8
0,8
s Es b,ult
1
-200
-300
1
0,8
0,76 0,782
0,8
0,595
1,141 1,144 1,150 1,155 1,159
1,164
1,623
-400
Относительная высота сжатой зоны бетона, ξ
В15
B20
B25
B30
B35
B40
А400
67

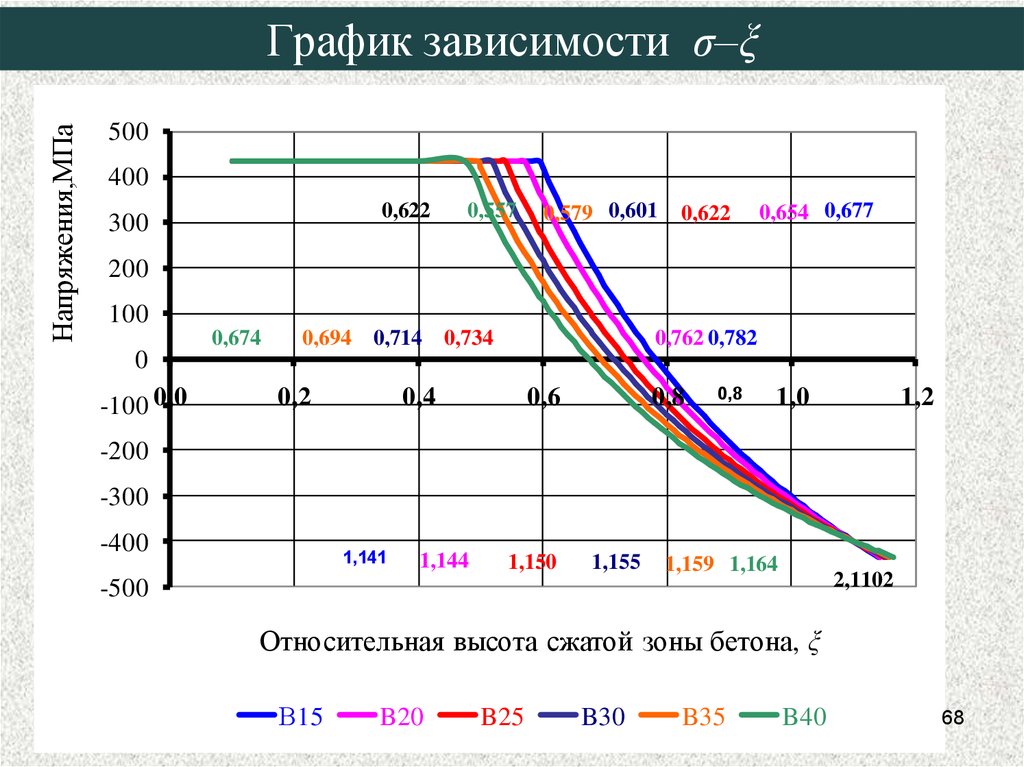
68. График зависимости σ–ξ

Напряжения,МПа
График зависимости σ–ξ
500
400
0,622
300
0,557
0,579 0,601
0,622
0,654 0,677
200
100
0,674
0,694
0,714
0,734
0,762 0,782
0
-100 0,0
0,2
0,4
0,6
0,8
0,8
1,0
1,2
-200
-300
-400
1,141
1,144
1,150
1,155
1,159 1,164
2,1102
-500
Относительная высота сжатой зоны бетона, ξ
В15
B20
B25
B30
B35
B40
68

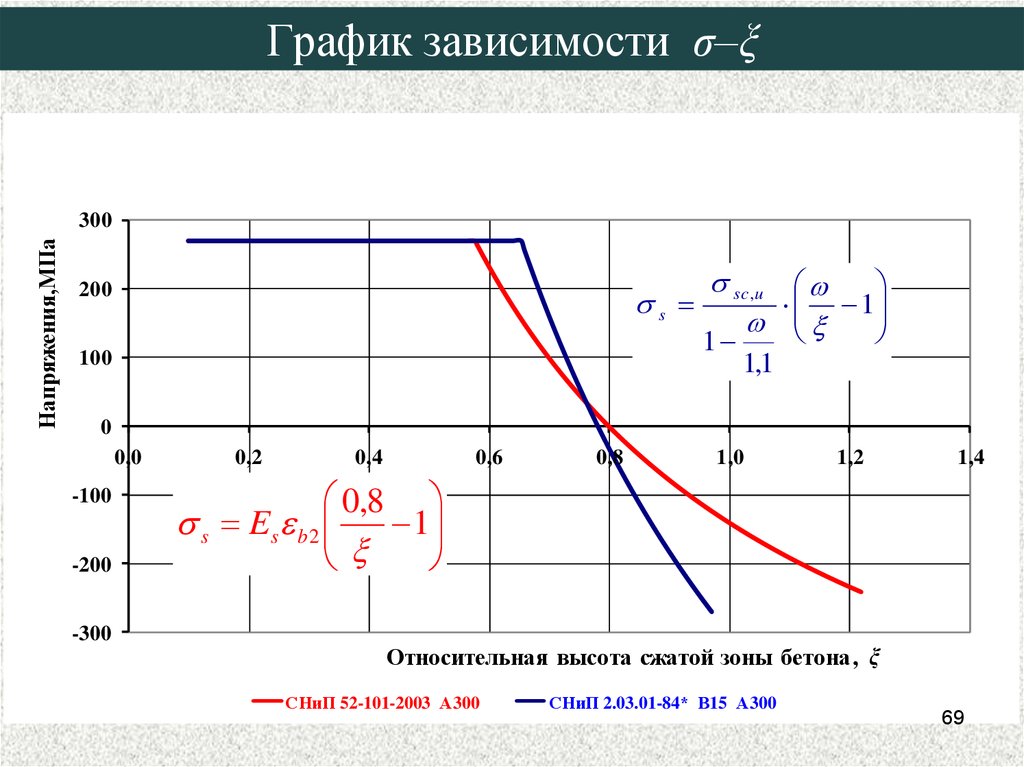
69. График зависимости σ–ξ

Напряжения,МПа
300
sc,u
s
200
1
100
1
1,1
0
0,0
-100
-200
-300
0,2
0,4
0,6
0,8
1,0
1,2
1,4
0,8
s Es b 2
1
Относительная высота сжатой зоны бетона, ξ
СНиП 52-101-2003 А300
СНиП 2.03.01-84* В15 А300
69

70. График зависимости σ–ξ

400
Напряжения,МПа
300
sc,u
s
200
1
100
1
1,1
0
0,0
0,2
0,4
0,6
0,8
1,0
1,2
1,4
1,6
1,8
-100
-200
-300
0,8
s Es b 2
1
-400
Относительная высота сжатой зоны бетона, ξ
"СНиП 52-101-2003 A400"
СНиП 2.03.01-84* В15 А400
70

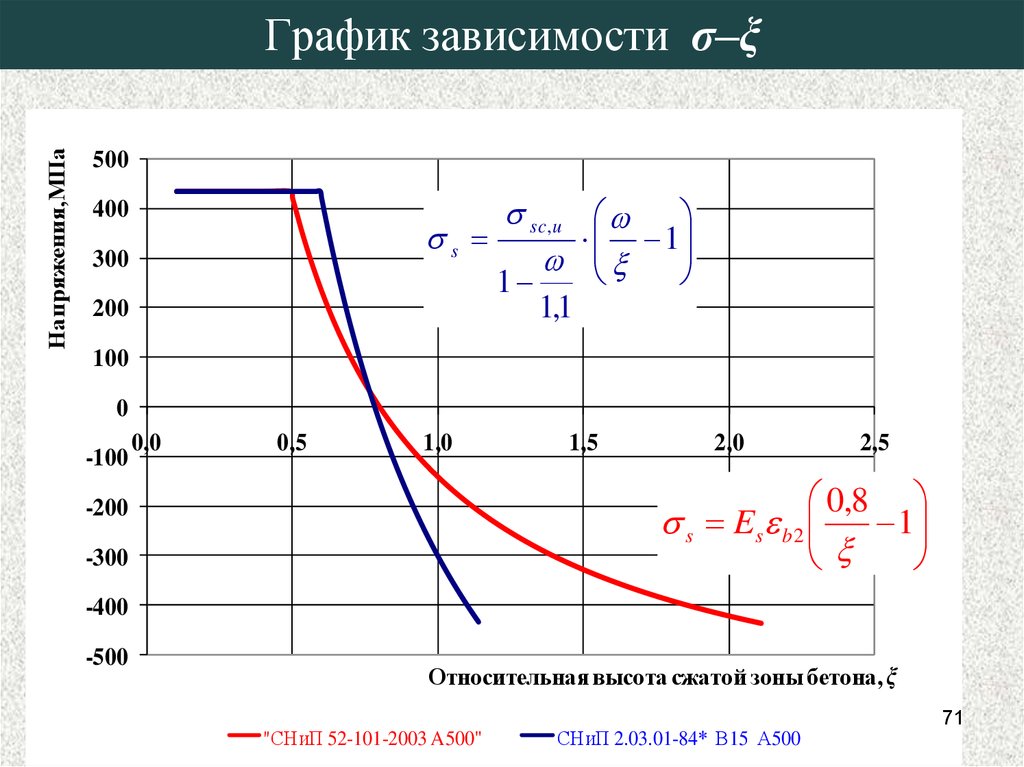
71. График зависимости σ–ξ

Напряжения,МПа
График зависимости σ–ξ
500
sc,u
s
1
1
1,1
400
300
200
100
0
-100
0,0
0,5
1,0
1,5
2,0
2,5
0,8
s Es b 2
1
-200
-300
-400
-500
Относительная высота сжатой зоны бетона, ξ
"СНиП 52-101-2003 A500"
СНиП 2.03.01-84* В15 А500
71

72.

График зависимости σ – ξ
Напряжения,МПа
500
0,493
0,474
0,495
400
0,517 0,539
0,571 0,595
sc,u
s
1
1
1,1
300
200
100
0
0,674 0,694
-100 0,0
-200
0,714
0,8
0,2
0,4
0,6
0,8
0,734 0,762 0,782
1,0
1,2
02,0
,8 2,2
s Es b 2
1
1,4
1,6
1,8
-300
-400
1,141 1,144 1,150
2,110
1,155 1,159 1,164
-500
Относительная высота сжатой зоны бетона, ξ
В15
B20
B25
B30
B35
B40
А500
72

73.

График зависимости σ – ξ
Напряжения,МПа
500
0,8
s Es b,ult
1
0,493
400
0,577
300
0,531
0,493
200
100
0,800
0
-100 0,0
0,2
0,4
0,6
0,8
1,0
1,2
1,4
1,6
1,8
2,0
2,2
1,155
-200
1,302
-300
1,623
-400
2,113
-500
Относительная высота сжатой зоны бетона, ξ
А500
А400
А300
А240
73

74.

Зависимость R от расчетного сопротивления бетона
Максимальный процент армирования, %
10
СНиП 52-101-03 А240
Rb
R R
Rs
9
8
7
СНиП 2.03.01-84* А240
СНиП 52-101-03 А300
СНиП 2.03.01-84* А300
6
5
4
3
2
1
5,0
10,0
15,0
20,0
25,0
30,0
35,0
Rb, МПа
74

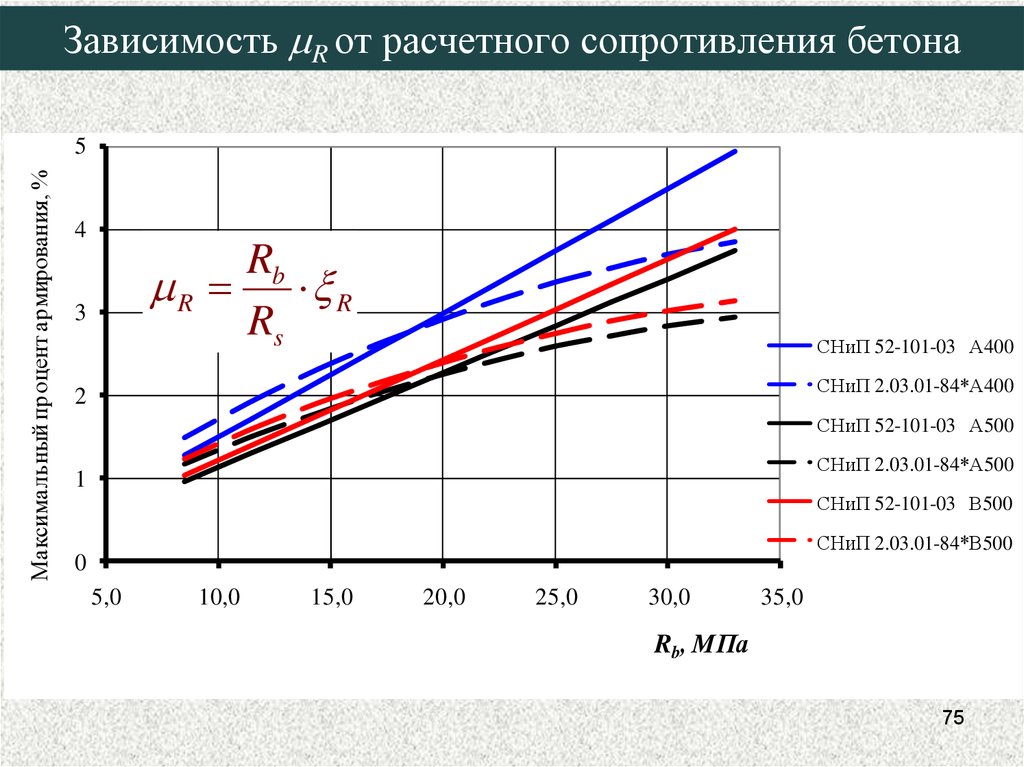
75. Зависимость mR от расчетного сопротивления бетона

Зависимость R от расчетного сопротивления бетона
Максимальный процент армирования, %
5
4
Rb
R R
Rs
3
СНиП 52-101-03 А400
СНиП 2.03.01-84*А400
2
СНиП 52-101-03 А500
СНиП 2.03.01-84*А500
1
СНиП 52-101-03 В500
СНиП 2.03.01-84*В500
0
5,0
10,0
15,0
20,0
25,0
30,0
35,0
Rb, МПа
75

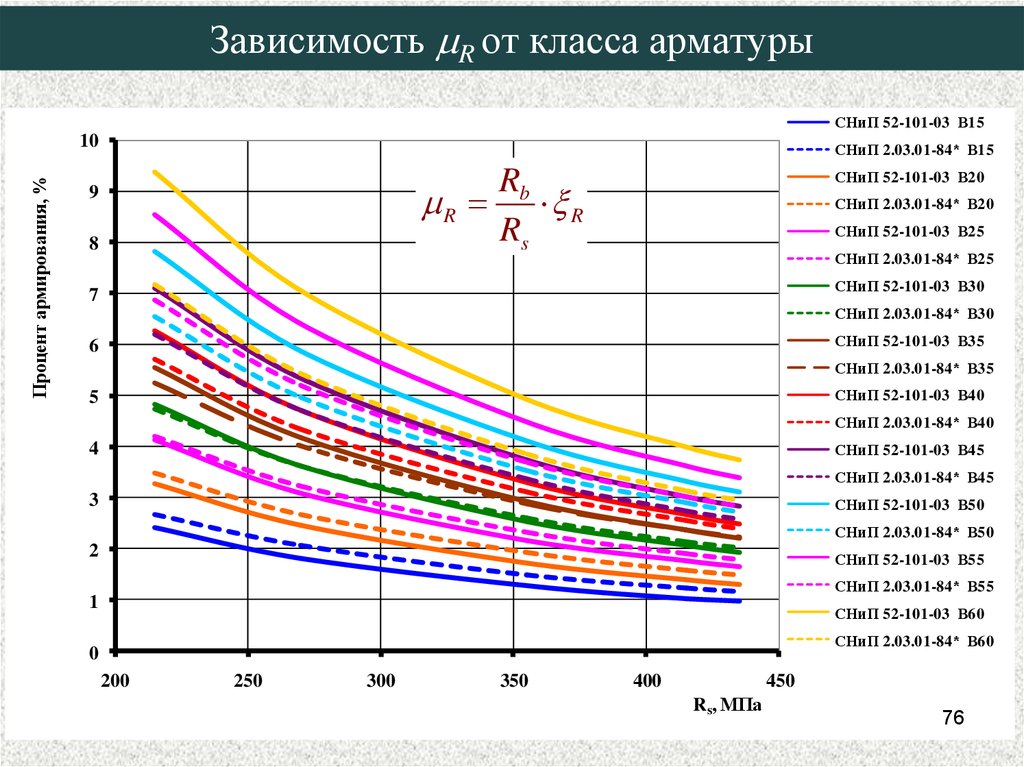
76. Зависимость mR от класса арматуры

Зависимость R от класса арматуры
СНиП 52-101-03 В15
Процент армирования, %
10
СНиП 2.03.01-84* В15
Rb
R R
Rs
9
8
СНиП 52-101-03 В20
СНиП 2.03.01-84* В20
СНиП 52-101-03 В25
СНиП 2.03.01-84* В25
СНиП 52-101-03 В30
7
СНиП 2.03.01-84* В30
СНиП 52-101-03 В35
6
СНиП 2.03.01-84* В35
СНиП 52-101-03 В40
5
СНиП 2.03.01-84* В40
4
СНиП 52-101-03 В45
СНиП 2.03.01-84* В45
3
СНиП 52-101-03 В50
СНиП 2.03.01-84* В50
2
СНиП 52-101-03 В55
СНиП 2.03.01-84* В55
1
СНиП 52-101-03 В60
СНиП 2.03.01-84* В60
0
200
250
300
350
400
450
Rs, МПа
76

77. Зависимость mR от класса арматуры

Зависимость R от класса арматуры
9
СНиП 52-101-03 В15
8
СНиП 2.03.01-84* В15
7
6
5
4
3
2
1
0
А240
А300
А400
В500
А500
77

78. Зависимость mR от класса арматуры

Зависимость R от класса арматуры
9
СНиП 52-101-03 В20
8
СНиП 2.03.01-84* В20
7
6
5
4
3
2
1
0
А240
А300
А400
В500
А500
78

79. Зависимость mR от класса арматуры

Зависимость R от класса арматуры
9
СНиП 52-101-03 В25
8
СНиП 2.03.01-84* В25
7
6
5
4
3
2
1
0
А240
А300
А400
В500
А500
79

80. Зависимость mR от класса арматуры

Зависимость R от класса арматуры
9
СНиП 52-101-03 В30
8
СНиП 2.03.01-84* В30
7
6
5
4
3
2
1
0
А240
А300
А400
В500
А500
80

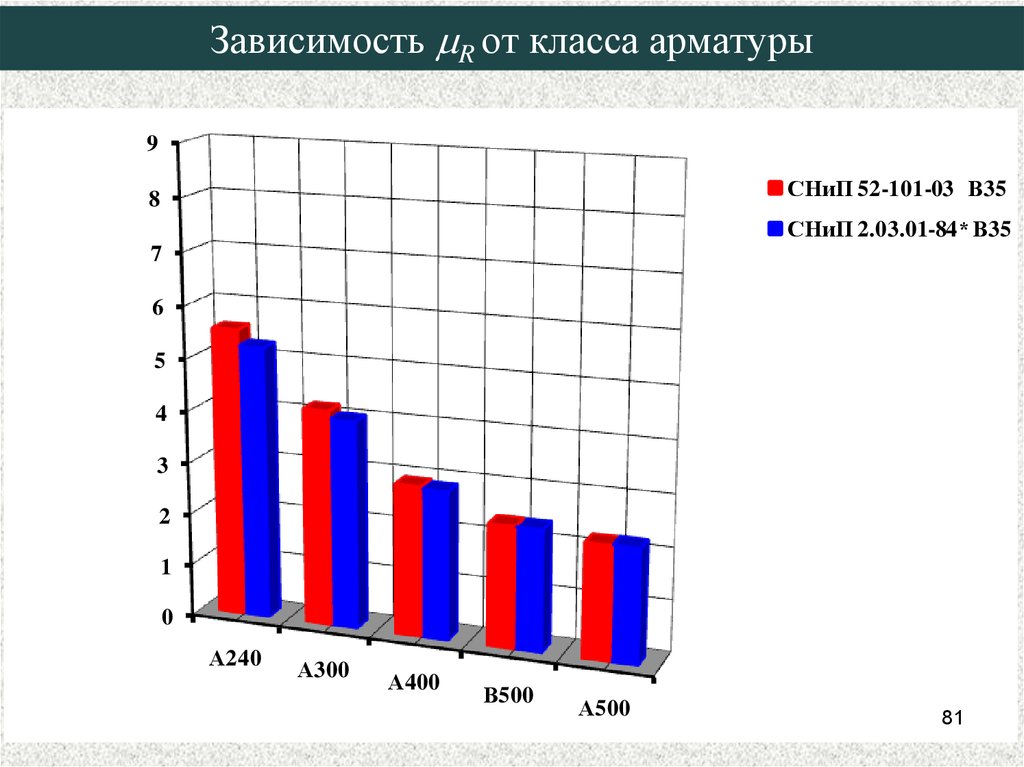
81. Зависимость mR от класса арматуры

Зависимость R от класса арматуры
9
СНиП 52-101-03 В35
8
СНиП 2.03.01-84* В35
7
6
5
4
3
2
1
0
А240
А300
А400
В500
А500
81

82.

Зависимость R от класса арматуры
9
СНиП 52-101-03 В40
8
СНиП 2.03.01-84* В40
7
6
5
4
3
2
1
0
А240
А300
А400
В500
А500
82

83. Зависимость mR от класса арматуры

Зависимость R от класса арматуры
9
СНиП 52-101-03 В45
8
СНиП 2.03.01-84* В45
7
6
5
4
3
2
1
0
А240
А300
А400
В500
А500
83

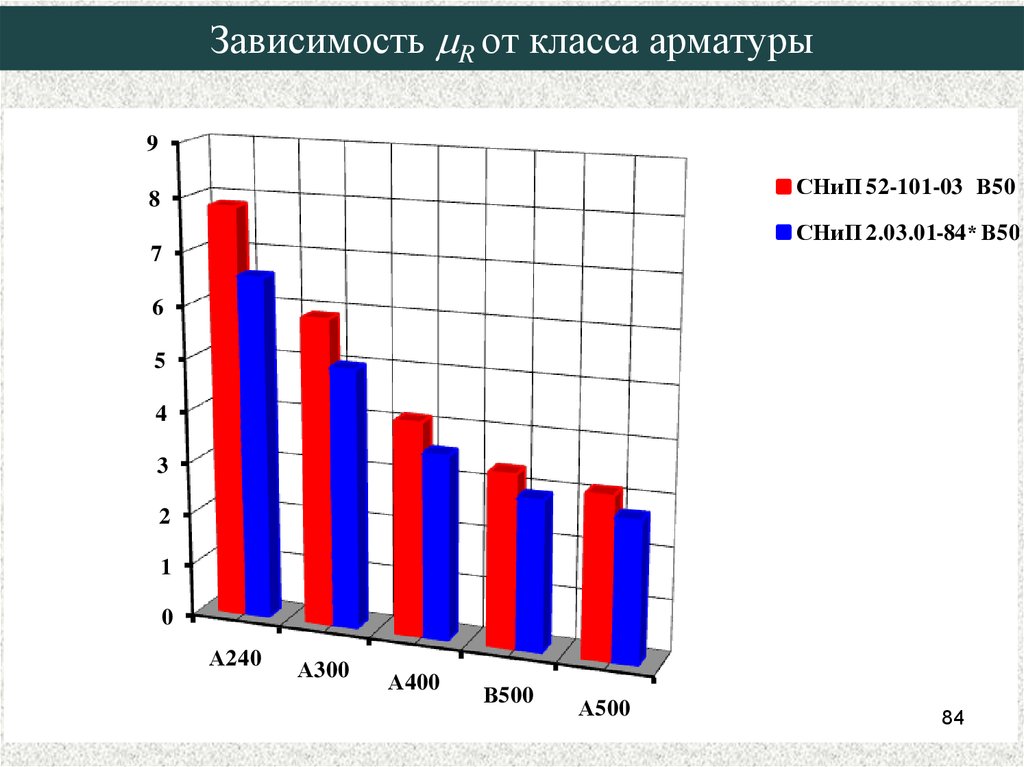
84. Зависимость mR от класса арматуры

Зависимость R от класса арматуры
9
СНиП 52-101-03 В50
8
СНиП 2.03.01-84* В50
7
6
5
4
3
2
1
0
А240
А300
А400
В500
А500
84

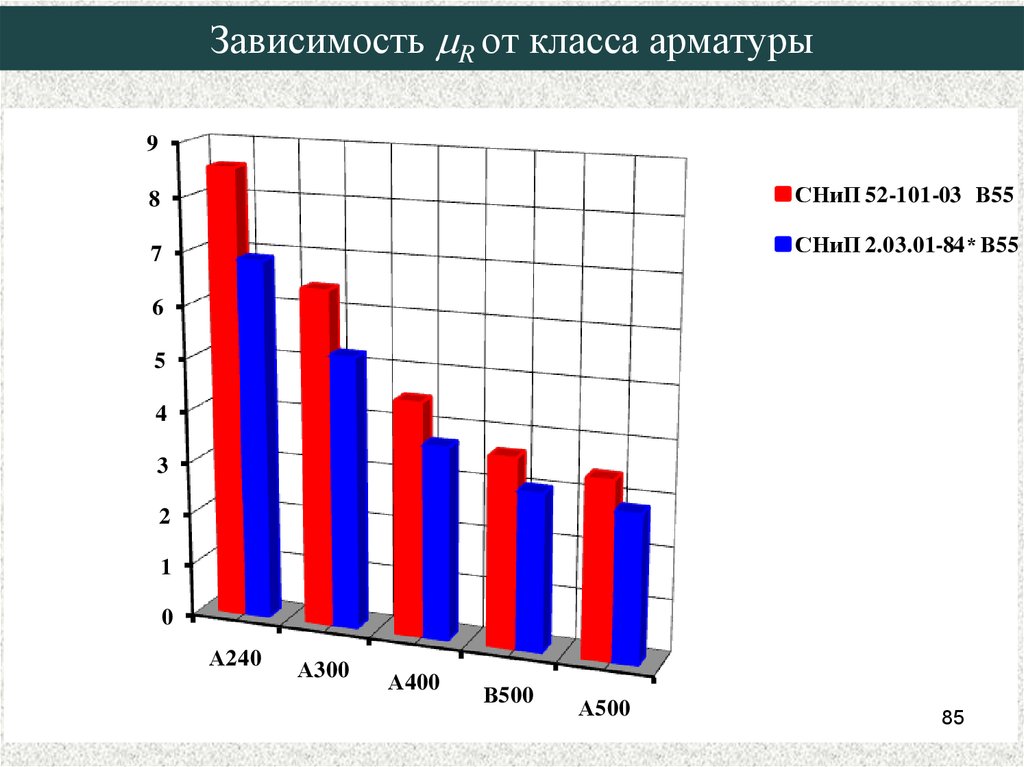
85. Зависимость mR от класса арматуры

Зависимость R от класса арматуры
9
8
СНиП 52-101-03 В55
7
СНиП 2.03.01-84* В55
6
5
4
3
2
1
0
А240
А300
А400
В500
А500
85

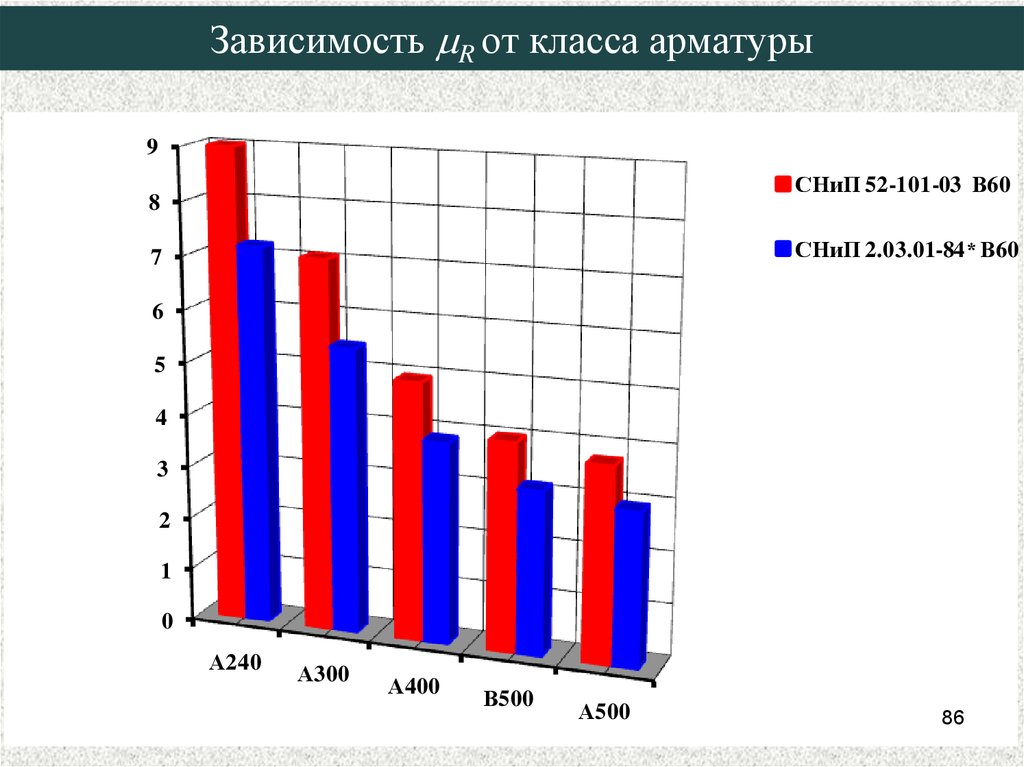
86. Зависимость mR от класса арматуры

Зависимость R от класса арматуры
9
СНиП 52-101-03 В60
8
СНиП 2.03.01-84* В60
7
6
5
4
3
2
1
0
А240
А300
А400
В500
А500
86

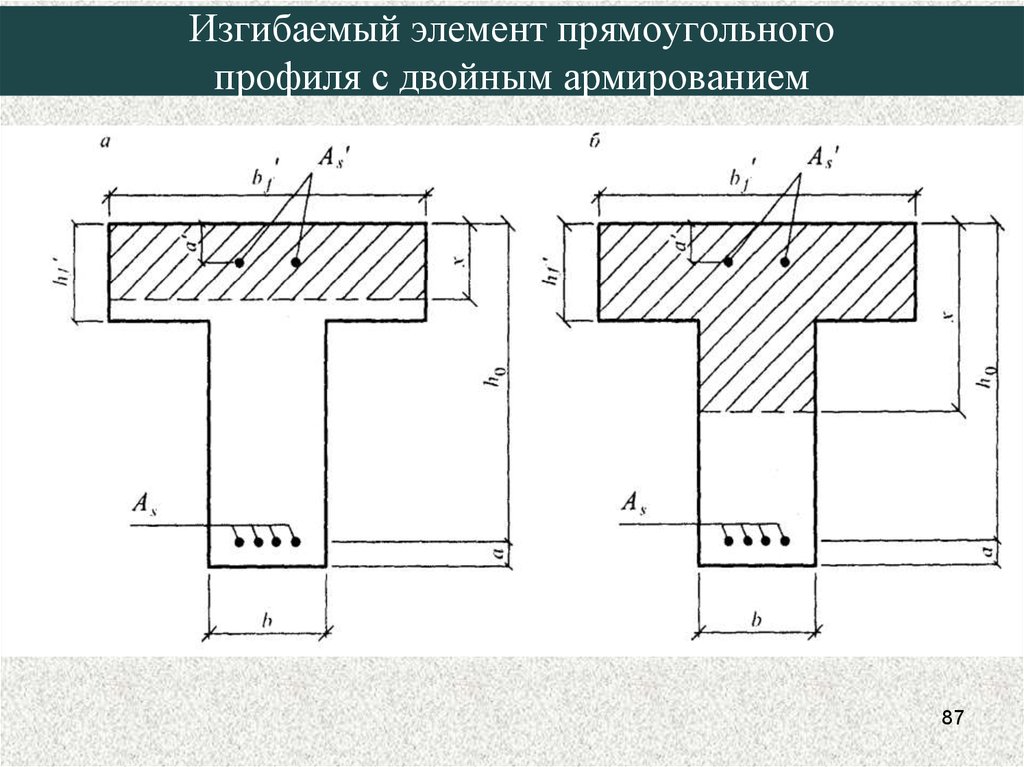
87.

Изгибаемый элемент прямоугольного
профиля с двойным армированием
87

88. Нелинейная деформационная модель расчета железобетонных конструкций по нормальным сечениям

Переход от эпюры напряжений в бетоне к обобщенным
внутренним усилиям определяют с помощью
процедуры численного интегрирования напряжений по
нормальному сечению.
88

89. Нелинейная деформационная модель расчета железобетонных конструкций по нормальным сечениям

Переход от эпюры напряжений в бетоне к
обобщенным внутренним усилиям определяют с
помощью процедуры численного интегрирования
напряжений по нормальному сечению.
Для этого нормальное сечение условно разделяют на
малые участки:
•при косом внецентренном сжатии (растяжении) и
косом изгибе - по высоте и ширине сечения;
•при внецентренном сжатии (растяжении) и изгибе
плоскости оси симметрии поперечного сечения
элемента - только по высоте сечения.
89

90. Нелинейная деформационная модель расчета железобетонных конструкций по нормальным сечениям

Переход от эпюры напряжений в бетоне к обобщенным внутренним усилиям
определяют с помощью процедуры численного интегрирования напряжений по
нормальному сечению.
Для этого нормальное сечение условно разделяют на малые участки:
– при косом внецентренном сжатии (растяжении) и косом изгибе - по высоте и
ширине сечения;
– при внецентренном сжатии (растяжении) и изгибе плоскости оси симметрии
поперечного сечения элемента - только по высоте сечения.
Напряжения в пределах малых участков принимают
равномерно распределенными (усредненными).
90

91. Нелинейная деформационная модель расчета железобетонных конструкций по нормальным сечениям

Переход от эпюры напряжений в бетоне к обобщенным внутренним усилиям
определяют с помощью процедуры численного интегрирования напряжений по
нормальному сечению.
Для этого нормальное сечение условно разделяют на малые участки:
• при косом внецентренном сжатии (растяжении) и косом изгибе - по высоте и
ширине сечения;
• при внецентренном сжатии (растяжении) и изгибе плоскости оси симметрии
поперечного сечения элемента - только по высоте сечения.
Напряжения в пределах малых участков принимают равномерно распределенными
(усредненными).
При
расчете
элементов
с
использованием
деформационной модели принимают:
• значения сжимающей продольной силы, а также
сжимающих напряжений и деформаций укорочения
бетона и арматуры - со знаком «минус»;
91

92. Нелинейная деформационная модель расчета железобетонных конструкций по нормальным сечениям

Переход от эпюры напряжений в бетоне к обобщенным внутренним усилиям
определяют с помощью процедуры численного интегрирования напряжений по
нормальному сечению.
Для этого нормальное сечение условно разделяют на малые участки:
• при косом внецентренном сжатии (растяжении) и косом изгибе - по высоте и
ширине сечения;
• при внецентренном сжатии (растяжении) и изгибе плоскости оси симметрии
поперечного сечения элемента - только по высоте сечения.
Напряжения в пределах малых участков принимают равномерно распределенными
(усредненными).
При расчете элементов с использованием деформационной модели принимают:
• значения сжимающей продольной силы, а также сжимающих напряжений и
деформаций укорочения бетона и арматуры - со знаком «минус»;
• значения растягивающей продольной силы, а также
растягивающих напряжений и деформаций удлинения
бетона и арматуры - со знаком «плюс».
92

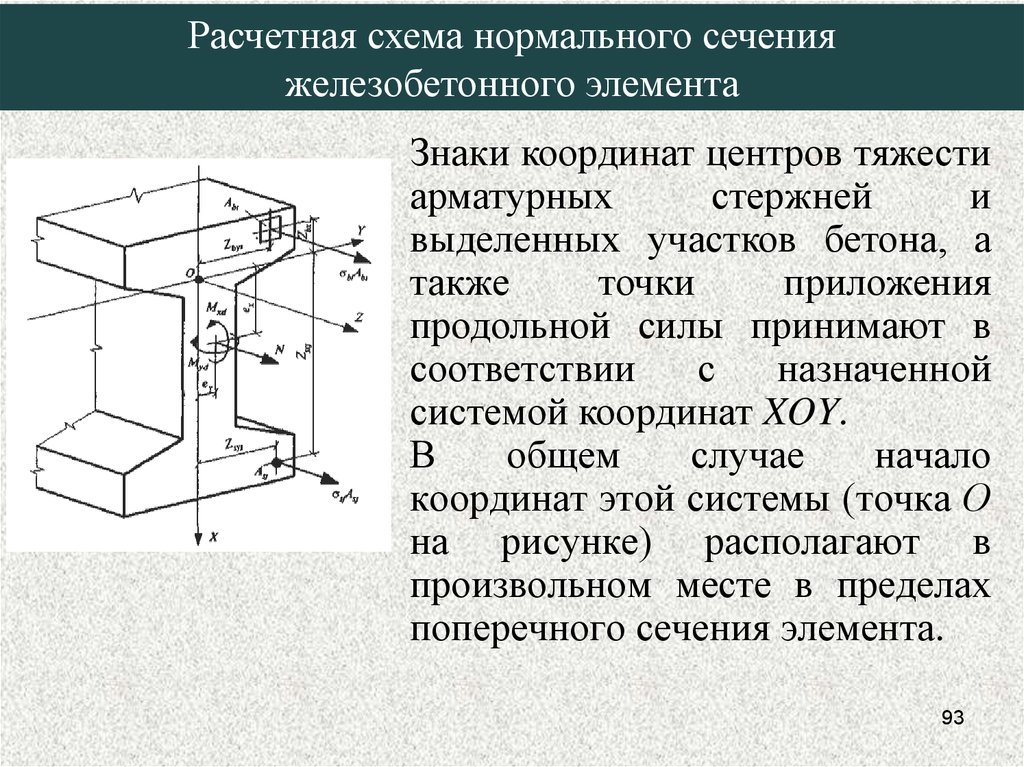
93.

Расчетная схема нормального сечения
железобетонного элемента
Знаки координат центров тяжести
арматурных
стержней
и
выделенных участков бетона, а
также
точки
приложения
продольной силы принимают в
соответствии
с
назначенной
системой координат XOY.
В
общем
случае
начало
координат этой системы (точка О
на рисунке) располагают в
произвольном месте в пределах
поперечного сечения элемента.
93

94. РАСЧЕТ ПРОЧНОСТИ НОРМАЛЬНЫХ СЕЧЕНИЙ НА ОСНОВЕ НЕЛИНЕЙНОЙ ДЕФОРМАЦИОННОЙ МОДЕЛИ

При расчете по прочности усилия и деформации в
сечении, нормальном к продольной оси элемента,
определяют на основе нелинейной деформационной
модели,
использующей
уравнения
равновесия
внешних сил и внутренних усилий в сечении
элемента, а также следующие положения:
94

95. РАСЧЕТ ПРОЧНОСТИ НОРМАЛЬНЫХ СЕЧЕНИЙ НА ОСНОВЕ НЕЛИНЕЙНОЙ ДЕФОРМАЦИОННОЙ МОДЕЛИ

При расчете по прочности усилия и деформации в
сечении, нормальном к продольной оси элемента,
определяют на основе нелинейной деформационной
модели,
использующей
уравнения
равновесия
внешних сил и внутренних усилий в сечении
элемента, а также следующие положения:
• распределение относительных деформаций бетона и
арматуры по высоте сечения элемента принимают по
линейному закону (гипотеза плоских сечений);
95

96. РАСЧЕТ ПРОЧНОСТИ НОРМАЛЬНЫХ СЕЧЕНИЙ НА ОСНОВЕ НЕЛИНЕЙНОЙ ДЕФОРМАЦИОННОЙ МОДЕЛИ

При расчете по прочности усилия и деформации в сечении, нормальном к
продольной оси элемента, определяют на основе нелинейной деформационной
модели, использующей уравнения равновесия внешних сил и внутренних усилий в
сечении элемента, а также следующие положения:
• распределение относительных деформаций бетона и арматуры по высоте сечения
элемента принимают по линейному закону (гипотеза плоских сечений);
• связь
между
осевыми
напряжениями
и
относительными деформациями бетона и арматуры
принимают
в
виде
диаграмм
состояния
(деформирования) бетона и арматуры;
96

97. РАСЧЕТ ПРОЧНОСТИ НОРМАЛЬНЫХ СЕЧЕНИЙ НА ОСНОВЕ НЕЛИНЕЙНОЙ ДЕФОРМАЦИОННОЙ МОДЕЛИ

При расчете по прочности усилия и деформации в сечении, нормальном к продольной
оси элемента, определяют на основе нелинейной деформационной модели,
использующей уравнения равновесия внешних сил и внутренних усилий в сечении
элемента, а также следующие положения:
• распределение относительных деформаций бетона и арматуры по высоте сечения
элемента принимают по линейному закону (гипотеза плоских сечений);
• связь между осевыми напряжениями и относительными деформациями бетона и
арматуры принимают в виде диаграмм состояния (деформирования) бетона и
арматуры;
• сопротивление бетона растянутой зоны допускается
не учитывать, принимая при εbi ≥ 0 напряжения σbi = 0.
97

98. РАСЧЕТ ПРОЧНОСТИ НОРМАЛЬНЫХ СЕЧЕНИЙ НА ОСНОВЕ НЕЛИНЕЙНОЙ ДЕФОРМАЦИОННОЙ МОДЕЛИ

При расчете по прочности усилия и деформации в сечении, нормальном к продольной
оси элемента, определяют на основе нелинейной деформационной модели,
использующей уравнения равновесия внешних сил и внутренних усилий в сечении
элемента, а также следующие положения:
• распределение относительных деформаций бетона и арматуры по высоте сечения
элемента принимают по линейному закону (гипотеза плоских сечений);
• связь между осевыми напряжениями и относительными деформациями бетона и
арматуры принимают в виде диаграмм состояния (деформирования) бетона и
арматуры;
• сопротивление бетона растянутой зоны допускается не учитывать, принимая при εbi
≥ 0 напряжения σbi = 0.
В отдельных случаях (например, изгибаемые и
внецентренно сжатые бетонные конструкции, в
которых не допускают трещины) расчет по прочности
производят с учетом работы растянутого бетона.
98

99. РАСЧЕТ ПРОЧНОСТИ НОРМАЛЬНЫХ СЕЧЕНИЙ НА ОСНОВЕ НЕЛИНЕЙНОЙ ДЕФОРМАЦИОННОЙ МОДЕЛИ

При расчете нормальных сечений по прочности в
общем случае используют:
• уравнения равновесия внешних сил и
внутренних усилий в нормальном сечении
элемента:
99

100. РАСЧЕТ ПРОЧНОСТИ НОРМАЛЬНЫХ СЕЧЕНИЙ НА ОСНОВЕ НЕЛИНЕЙНОЙ ДЕФОРМАЦИОННОЙ МОДЕЛИ

При расчете нормальных сечений по прочности в общем случае используют:
• уравнения равновесия внешних сил и внутренних усилий в нормальном сечении
элемента:
• уравнения, определяющие распределение деформаций
по сечению элемента:
1
1
bi 0 Z bxi Z byj
rx
ry
si 0
1
1
Z sxi Z syj
rx
ry
100

101. РАСЧЕТ ПРОЧНОСТИ НОРМАЛЬНЫХ СЕЧЕНИЙ НА ОСНОВЕ НЕЛИНЕЙНОЙ ДЕФОРМАЦИОННОЙ МОДЕЛИ

При расчете нормальных сечений по прочности в общем случае используют:
• уравнения равновесия внешних сил и внутренних усилий в нормальном сечении
элемента:
• уравнения, определяющие распределение деформаций по сечению элемента:
bi 0
1
1
1
1
Z bxi Z byj si 0 Z sxi Z syj
rx
ry
rx
ry
• зависимости, связывающие напряжения и
относительные деформации бетона и арматуры:
bi Eb bi bi sj Es sj sj
101

102. РАСЧЕТ ПРОЧНОСТИ НОРМАЛЬНЫХ СЕЧЕНИЙ НА ОСНОВЕ НЕЛИНЕЙНОЙ ДЕФОРМАЦИОННОЙ МОДЕЛИ

При расчете нормальных сечений по прочности в общем случае используют:
• уравнения равновесия внешних сил и внутренних усилий в нормальном сечении
элемента:
• уравнения, определяющие распределение деформаций по сечению элемента:
1
1
1
1
bi 0 Z bxi Z byj
si 0 Z sxi Z syj
rx
ry
rx
ry
• зависимости, связывающие напряжения и относительные деформации бетона и
арматуры:
E E
bi
M x M xd Nex
b bi bi
sj
M y M yd Ney
s sj sj
bi
si
bi
si
Eb bi
Es si
Расчет нормальных сечений железобетонных элементов
по прочности производят из условий
b,max b 2
s ,max s 2
102