ДЗ

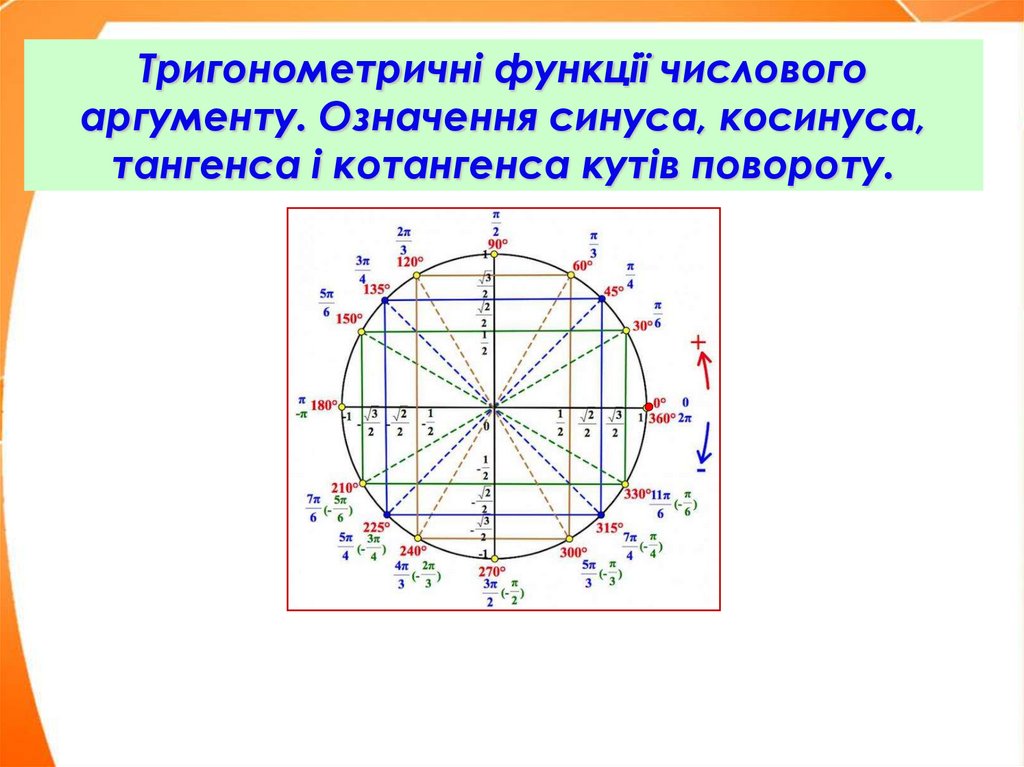
1. Тригонометричні функції числового аргументу. Означення синуса, косинуса, тангенса і котангенса кутів повороту.

2.

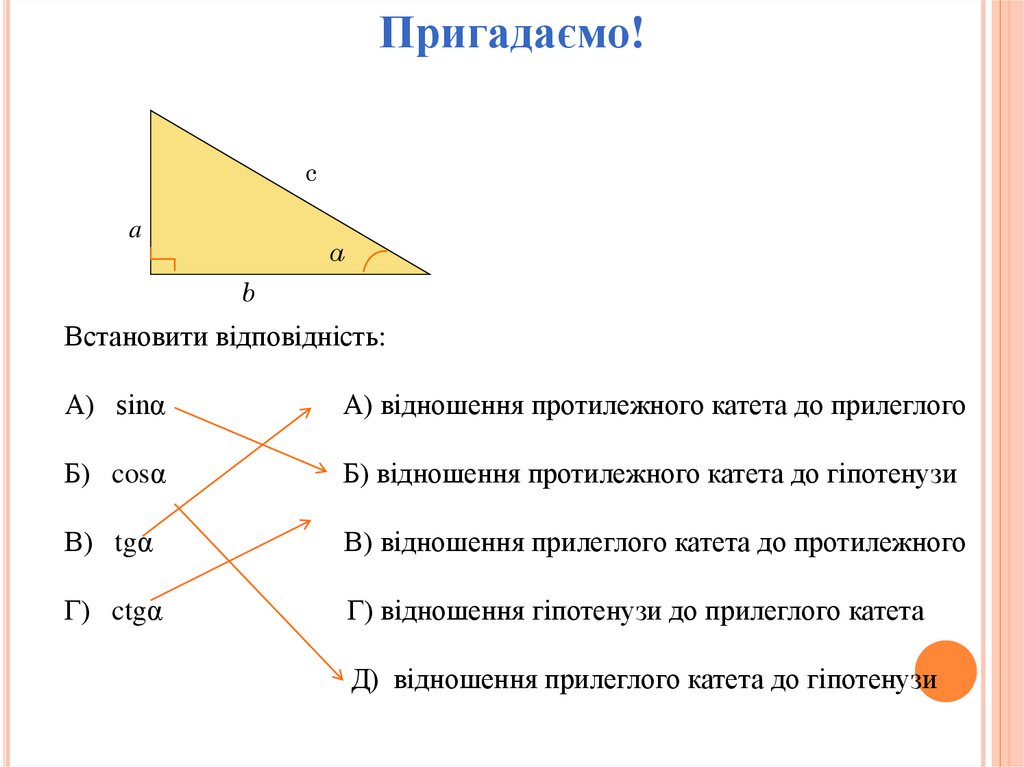
Пригадаємо!
c
a
α
b
Встановити відповідність:
А) sinα
А) відношення протилежного катета до прилеглого
Б) cosα
Б) відношення протилежного катета до гіпотенузи
В) tgα
В) відношення прилеглого катета до протилежного
Г) ctgα
Г) відношення гіпотенузи до прилеглого катета
Д) відношення прилеглого катета до гіпотенузи

3.

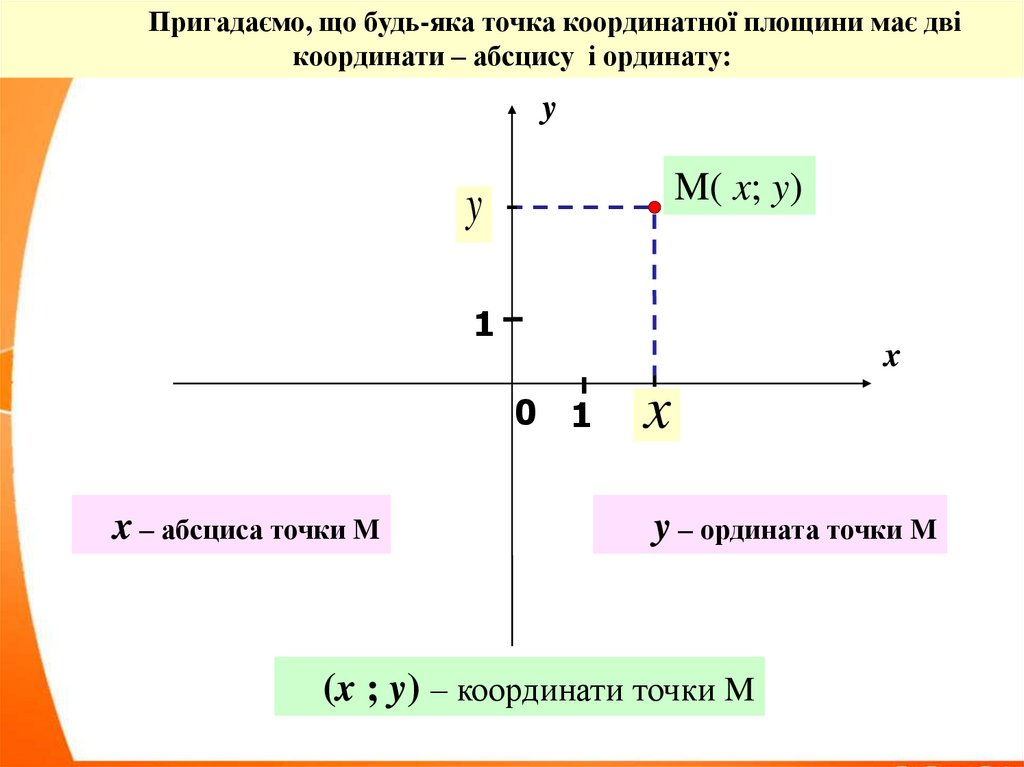
Пригадаємо, що будь-яка точка координатної площини має дві
координати – абсцису і ординату:
y
M( x; y)
y
1
x
0 1
x – абсциса точки M
x
y – ордината точки M
(x ; y) – координати точки M

4.

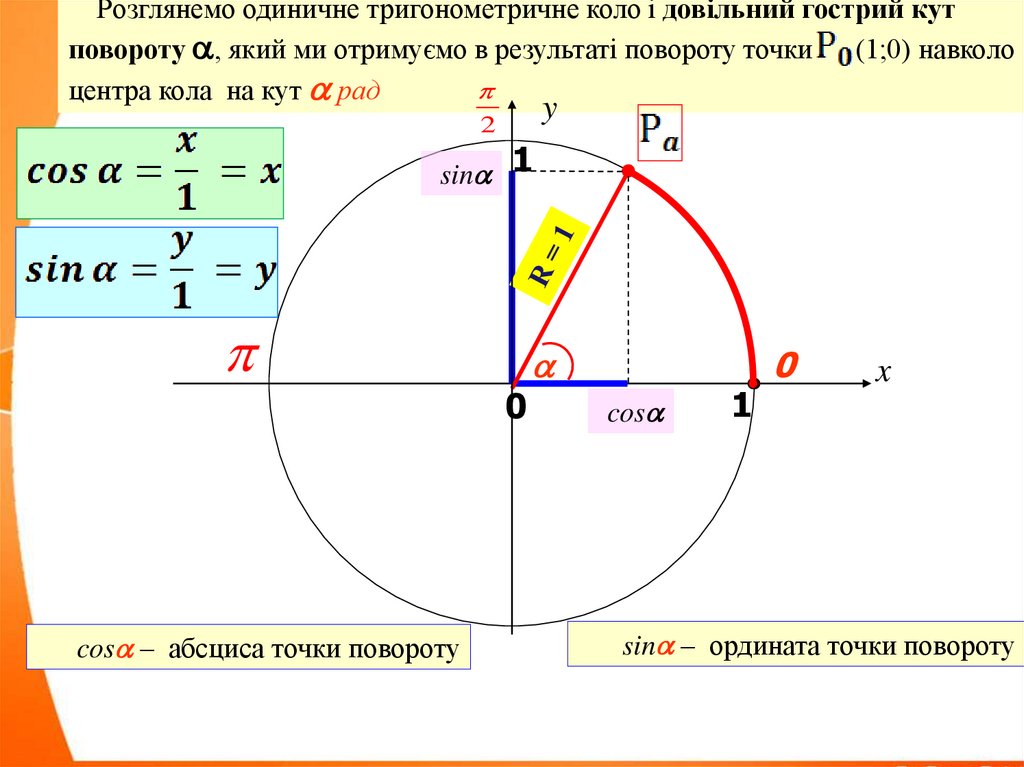
Розглянемо одиничне тригонометричне коло і довільний гострий кут
повороту , який ми отримуємо в результаті повороту точки (1;0) навколо
центра кола на кут рад
y
2
sin 1
0
cos – абсциса точки повороту
cos
1
0
x
sin – ордината точки повороту

5.

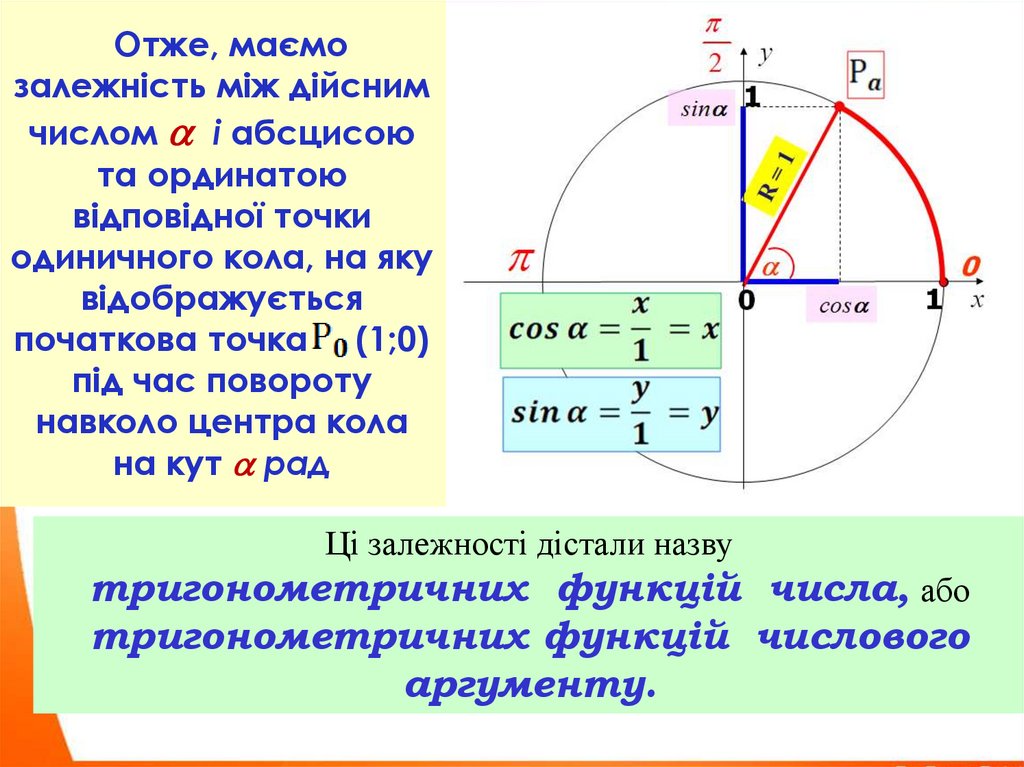
Отже, маємо
залежність між дійсним
числом і абсцисою
та ординатою
відповідної точки
одиничного кола, на яку
відображується
початкова точка (1;0)
під час повороту
навколо центра кола
на кут рад
Ці залежності дістали назву
тригонометричних функцій числа, або
тригонометричних функцій числового
аргументу.

6.

Синусом числа
називається ордината точки
одиничного кола, в яку переходить
початкова точка (1;0) під час
повороту навколо центра кола на
кут рад, і позначається sin .
Косинусом числа називається абсциса точки
одиничного кола, в яку переходить початкова точка
(1;0) під час повороту навколо центра кола на
кут рад, і позначається cos .
Тангенсом числа називається відношення
а котангенсом числа відношення
, і
позначаються вони відповідно tg і ctg .

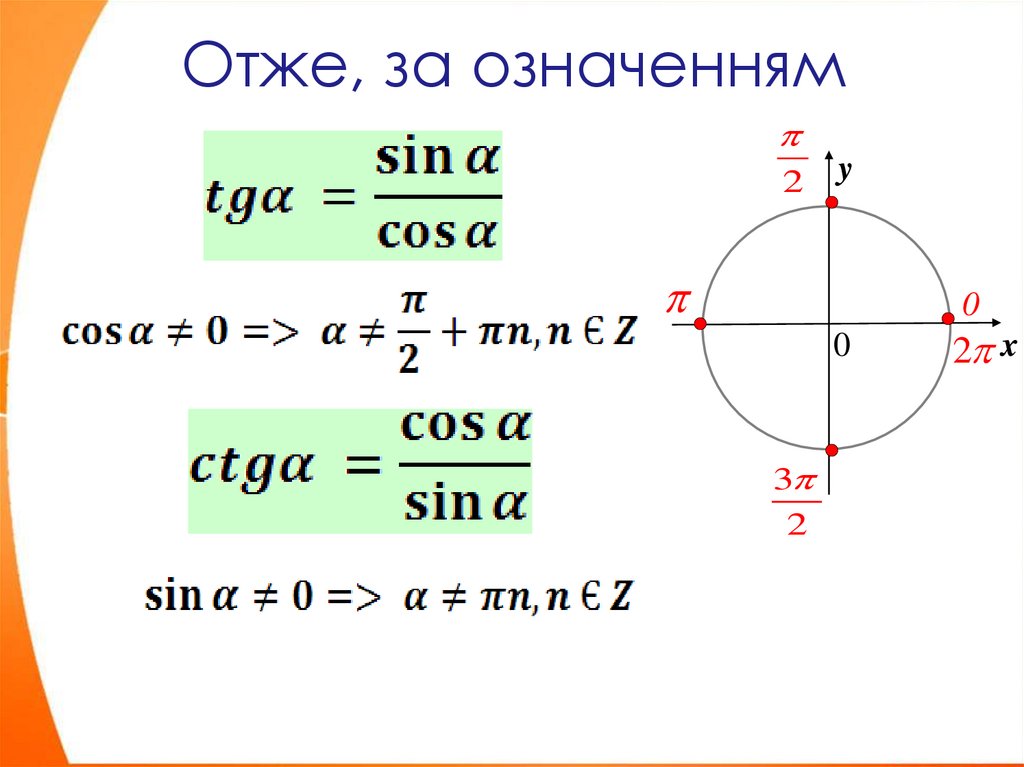
7. Отже, за означенням

2
y
0
0
3
2
2 x

8.

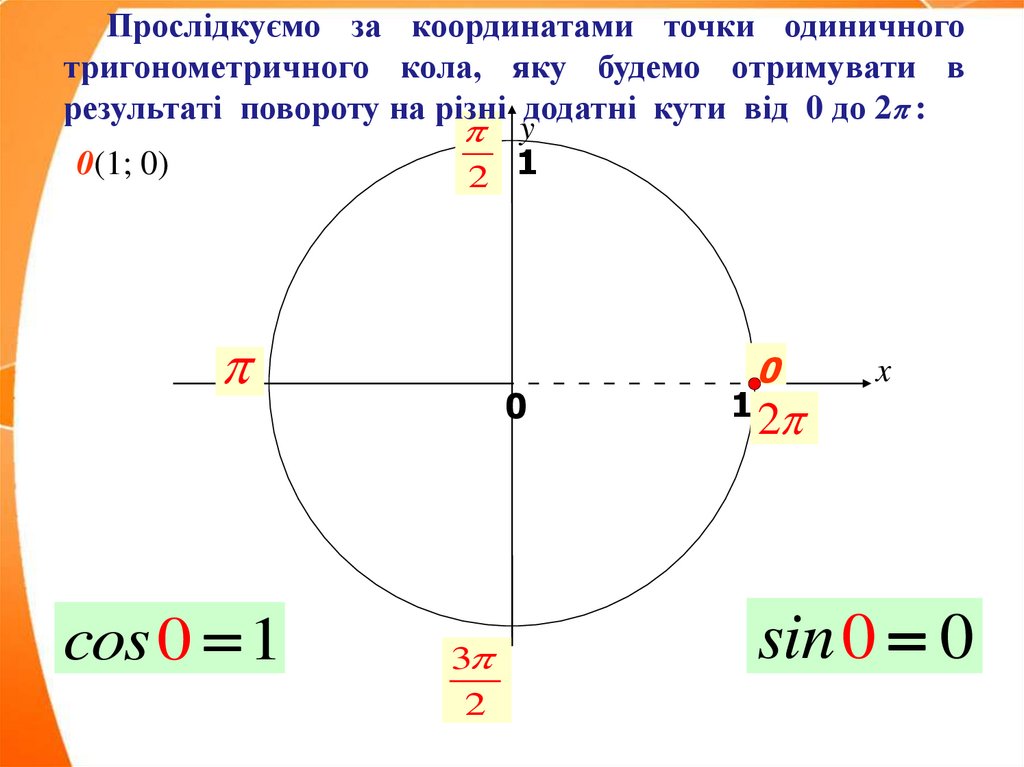
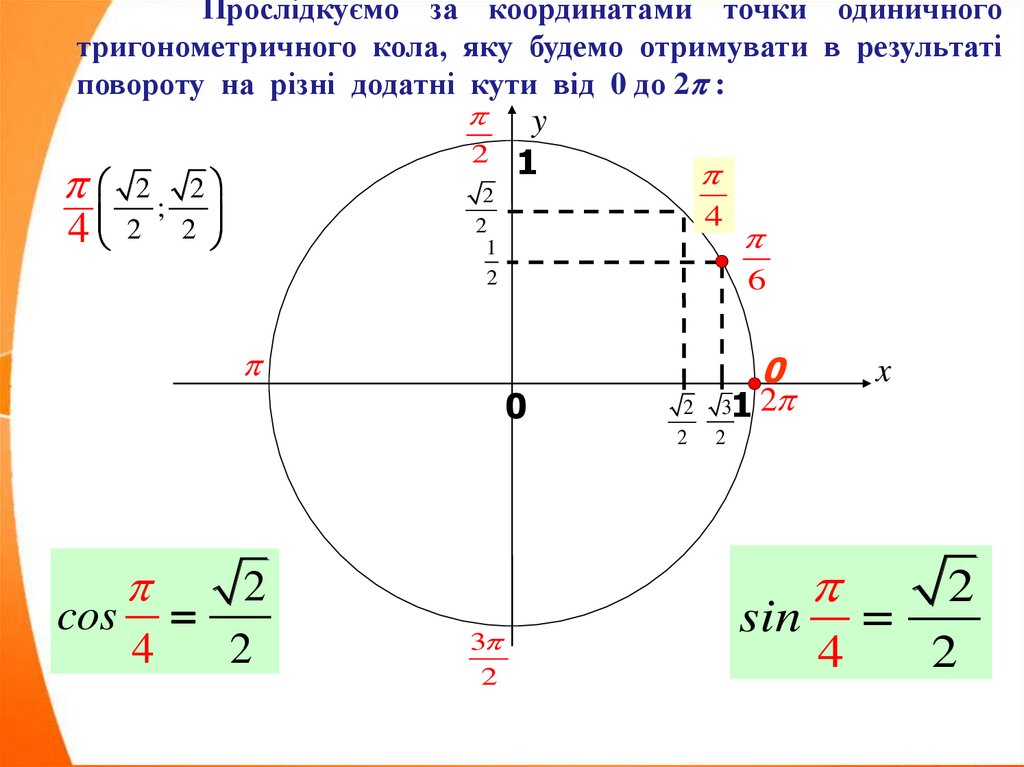
Прослідкуємо за координатами точки одиничного
тригонометричного кола, яку будемо отримувати в
результаті повороту на різні додатні кути від 0 до 2 :
y
0(1; 0)
2 1
cos 0 1
0
3
2
1
0
2
x
sin 0 0

9.

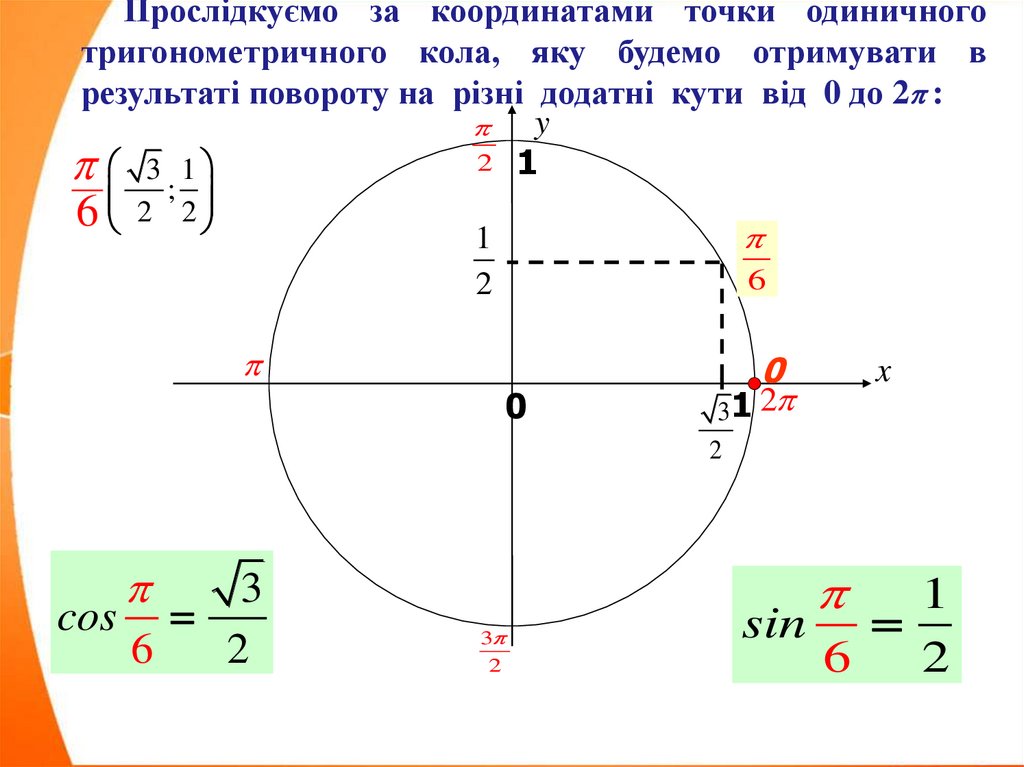
Прослідкуємо за координатами точки одиничного
тригонометричного кола, яку будемо отримувати в
результаті повороту на різні додатні кути від 0 до 2 :
y
2 1
3 1
;
6 2 2
1
2
6
0
0
3 1 2
x
2
3
cos
6
2
3
2
1
sin
6
2

10.

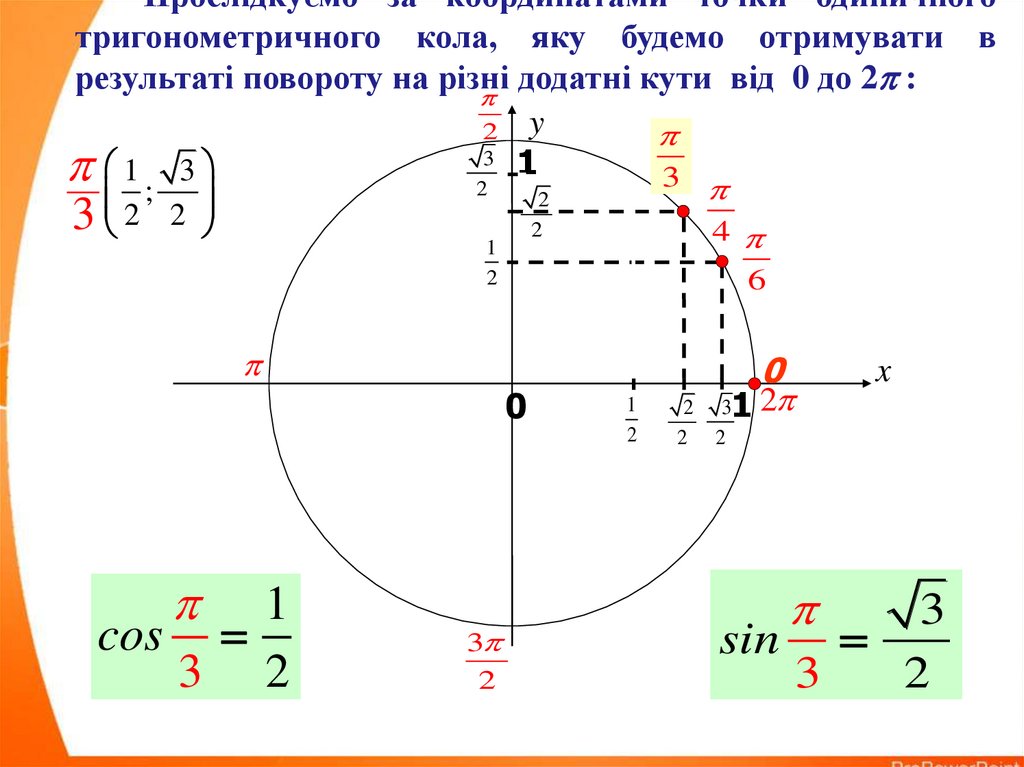
Прослідкуємо за координатами точки одиничного
тригонометричного кола, яку будемо отримувати в результаті
повороту на різні додатні кути від 0 до 2 :
2
2 ; 2
4 2
y
1
2
2
1
2
2
4
6
0
2
2
0
31 2
x
2
2
cos
4
2
3
2
2
sin
4
2

11.

Прослідкуємо за координатами точки одиничного
тригонометричного кола, яку будемо отримувати в
результаті повороту на різні
додатні кути від 0 до 2 :
2 y
3 1
1 3
3
;
2
2
3
2
2
2
1
2
4
6
0
1
cos
3 2
3
2
1
2
2
2
0
31 2
x
2
3
sin
3
2

12.

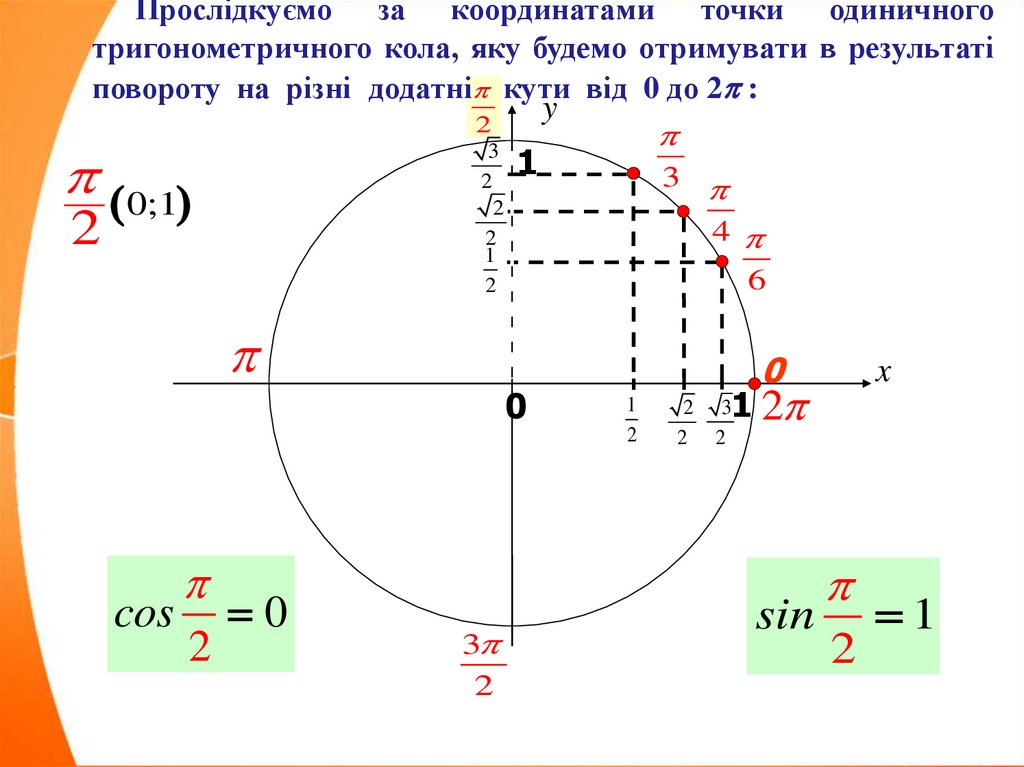
Прослідкуємо за координатами точки одиничного
тригонометричного кола, яку будемо отримувати в результаті
повороту на різні додатні кути від 0 до 2 :
y
2
0;1
3
2
2
2
1
2
2
1
3
4
6
0
cos
2
0
3
2
0
1
2
2
2
x
1 2
3
2
sin
2
1

13.

2
3 3
4
3
4
0
1
2
2
2
2
-1
3
2
6
1
2
-1 2
2
2
1
2
3
2
1
3
2
5
6
y
2
1
2
3
2
0
2 3 1 2
2
2
x

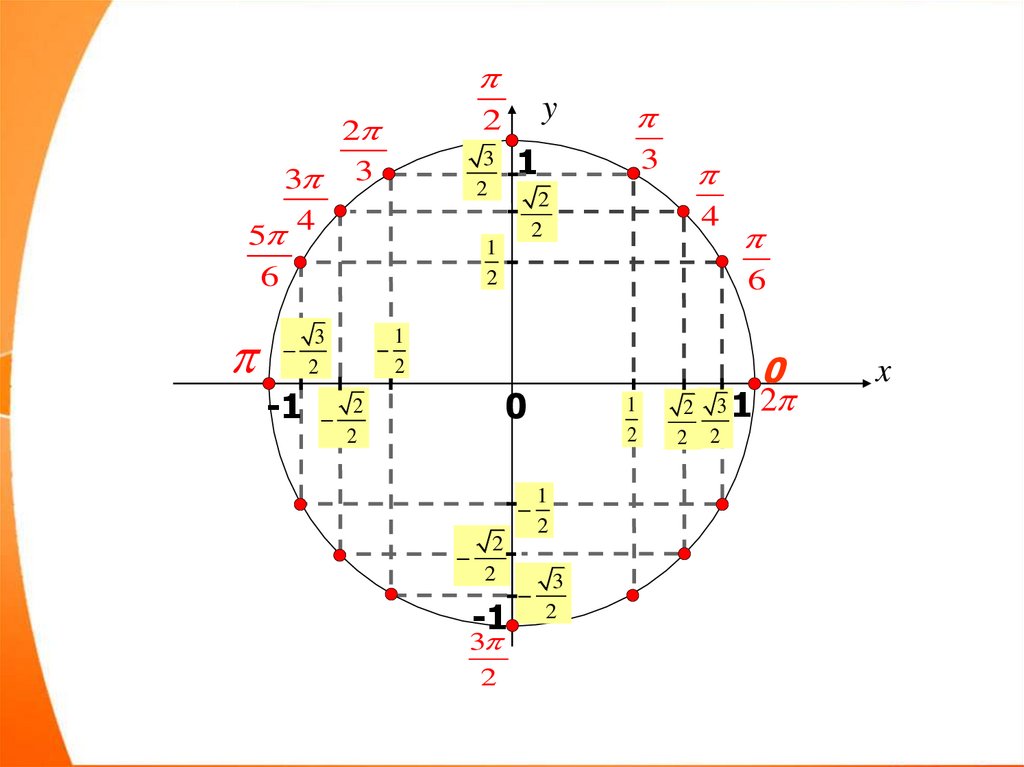
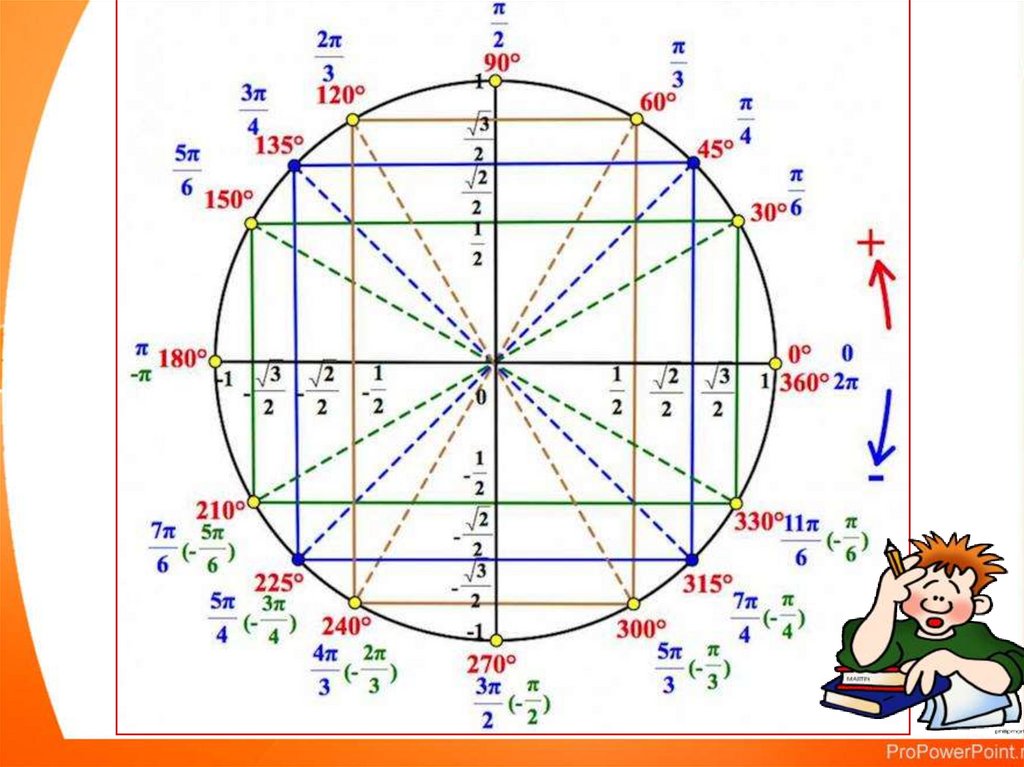
14. Перевірте:

3
6 2
2 2
4 2
1
2 1 3
3 2
3
4 2
0
7 3
6 2
5 2
2
4 2
6 2
4 1
3
3 2
3
1
2
5 1
3
3 2
7 2
2
4 2
11 3
6 2
0 0
2
1
3
3 2 2
3
2 2 5

15.

16.

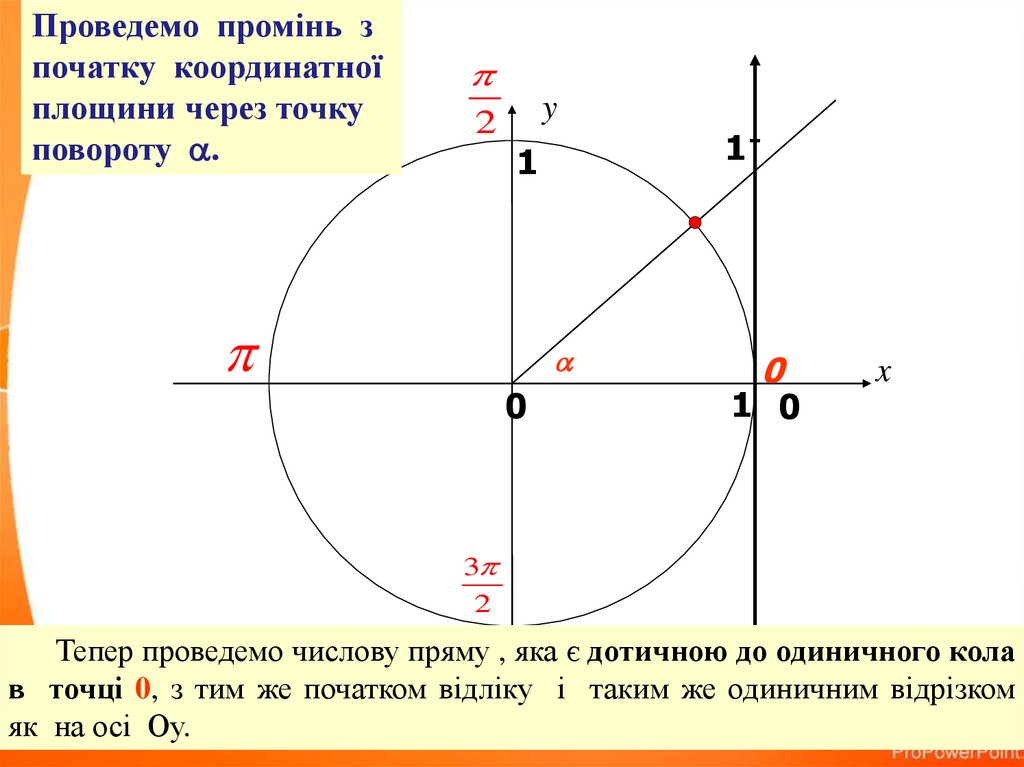
Проведемо промінь з
початку координатної
площини через точку
повороту .
2
y
1
0
1
0
1 0
x
3
2
Тепер проведемо числову пряму , яка є дотичною до одиничного кола
в точці 0, з тим же початком відліку і таким же одиничним відрізком
як на осі Оу.

17.

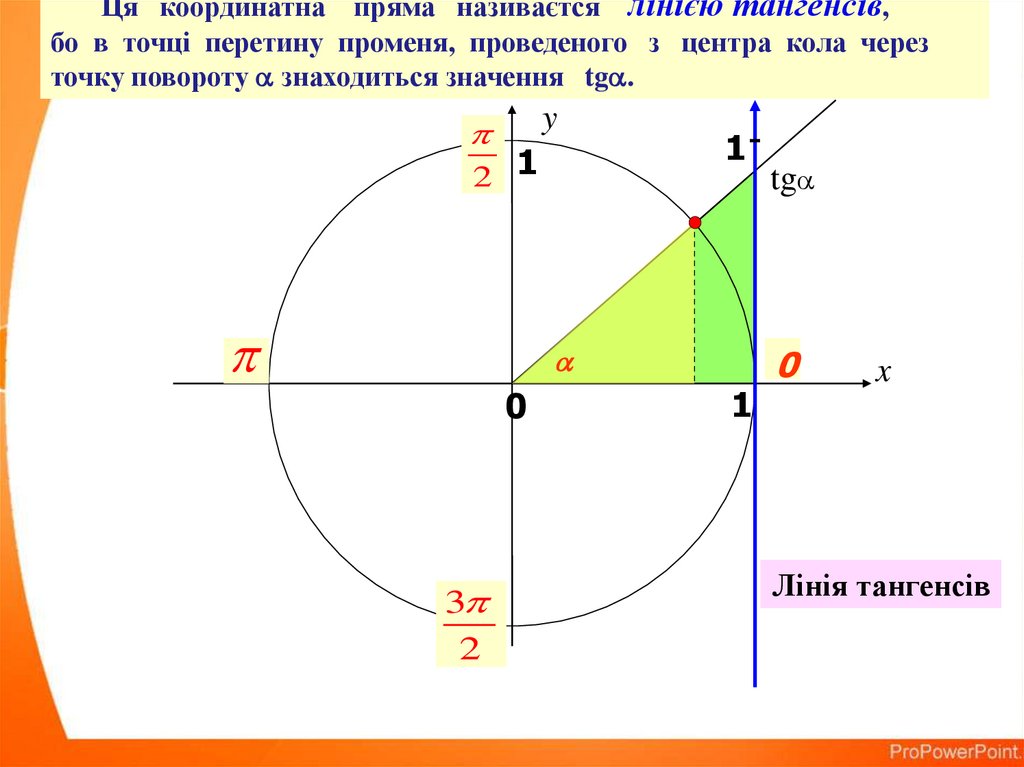
Ця координатна пряма називаєтся лінією тангенсів,
бо в точці перетину променя, проведеного з центра кола через
точку повороту знаходиться значення tg .
y
2 1
1
0
3
2
1
tg
0
x
Лінія тангенсів

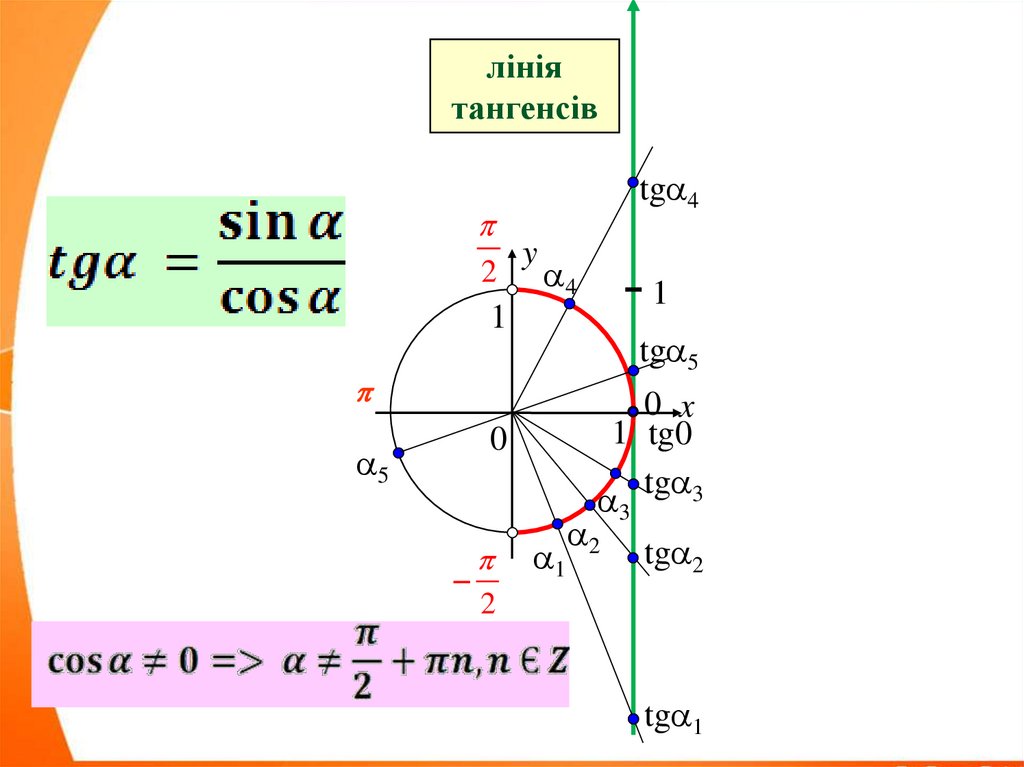
18.

лінія
тангенсів
tg 4
y
2 4
1
1
tg 5
0 x
1 tg0
tg 3
3
0
5
1
2
tg 2
2
tg 1

19.

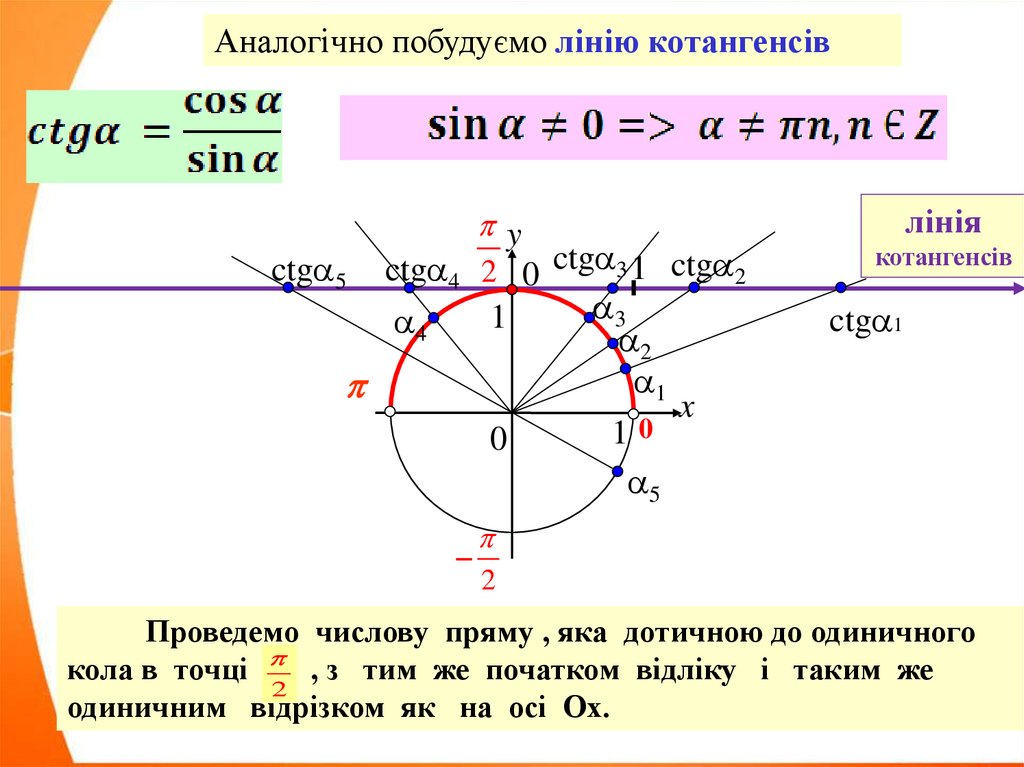
Аналогічно побудуємо лінію котангенсів
y
ctg 5 ctg 4 2 0 ctg 3 1 ctg 2
3
1
4
2
1
x
10
0
5
лінія
котангенсів
ctg 1
2
Проведемо числову пряму , яка дотичною до одиничного
кола в точці , з тим же початком відліку і таким же
2
одиничним відрізком як на осі Ох.

20.

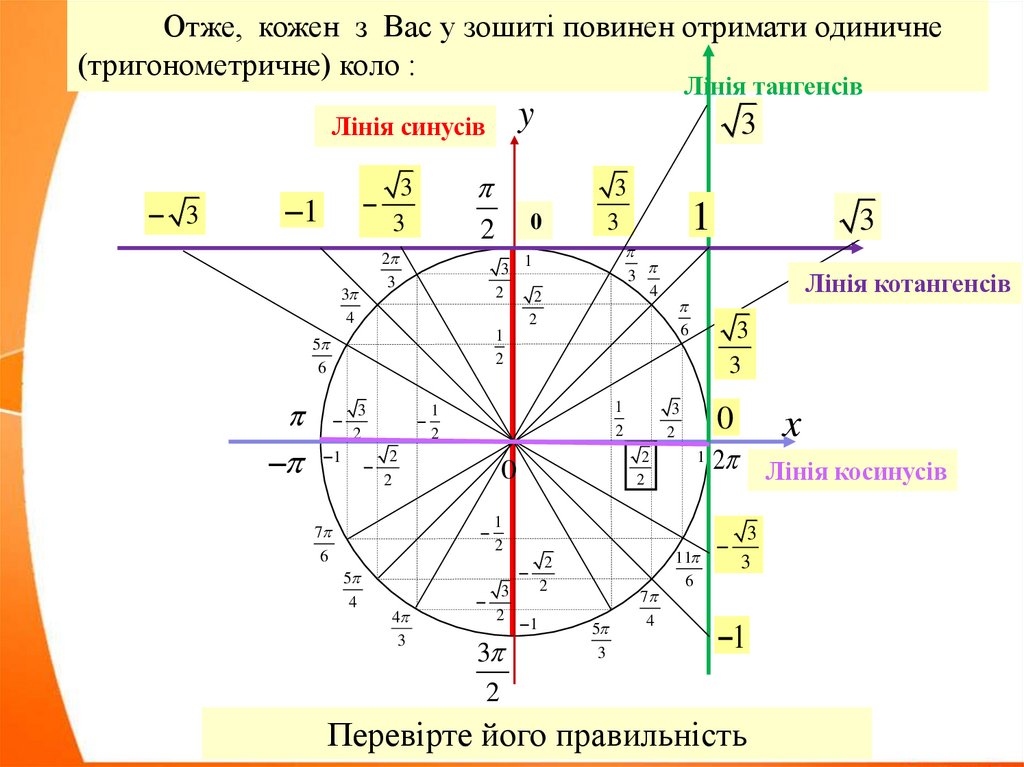
Отже, кожен з Вас у зошиті повинен отримати одиничне
(тригонометричне) коло :
y
Лінія синусів
3
1
3
4
3
3
2
2
3
Лінія тангенсів
3
0
3
2
3
3
1
3
4
1
2
2
1
2
5
6
1
23
2
1 22
7
6
1
2
5
4
4
3
3
2
3
2
1
3
3
3
2
1
2
Лінія котангенсів
6
0
2
2
0
3
1
2 Лінія косинусів
3
11
3
2
2
5
3
7
4
x
6
1
Перевірте його правильність

21.

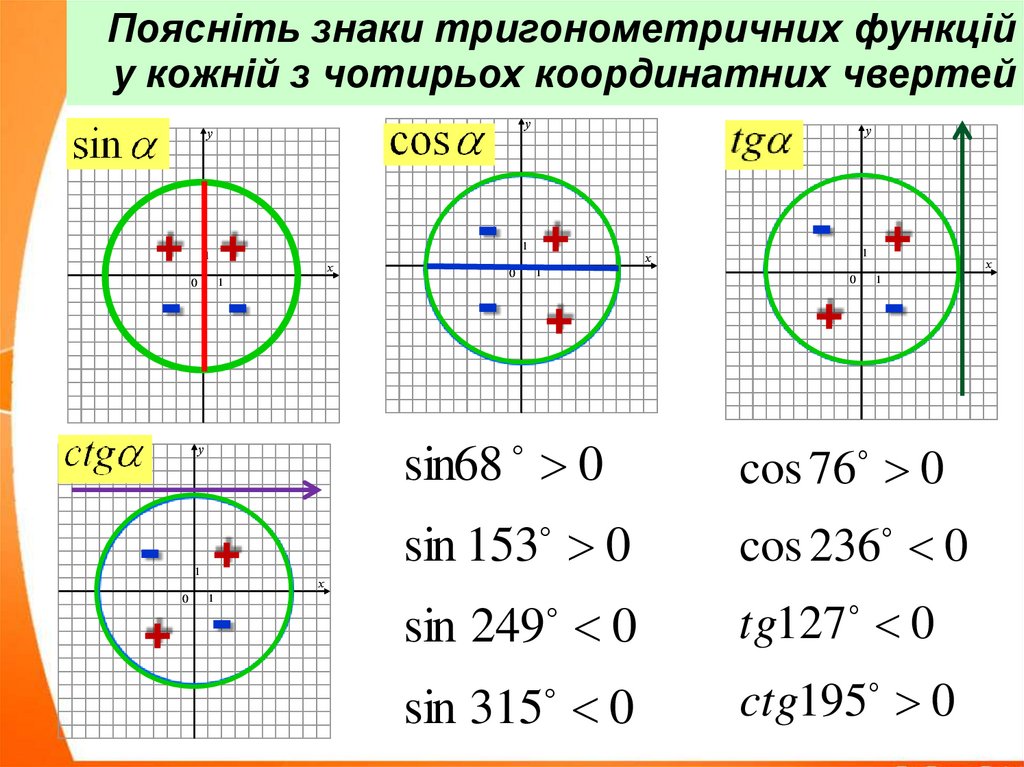
Поясніть знаки тригонометричних функцій
у кожній з чотирьох координатних чвертей
у
у
+ +
х
1
- -
0
1
- +
+ 1
1
х
- +
+ 1
1
0
sin68 0
cos 76 0
sin 153 0
cos 236 0
sin 249 0
tg127 0
sin 315 0
ctg195 0
у
0
- +
- +
1
1
0
у
х
х

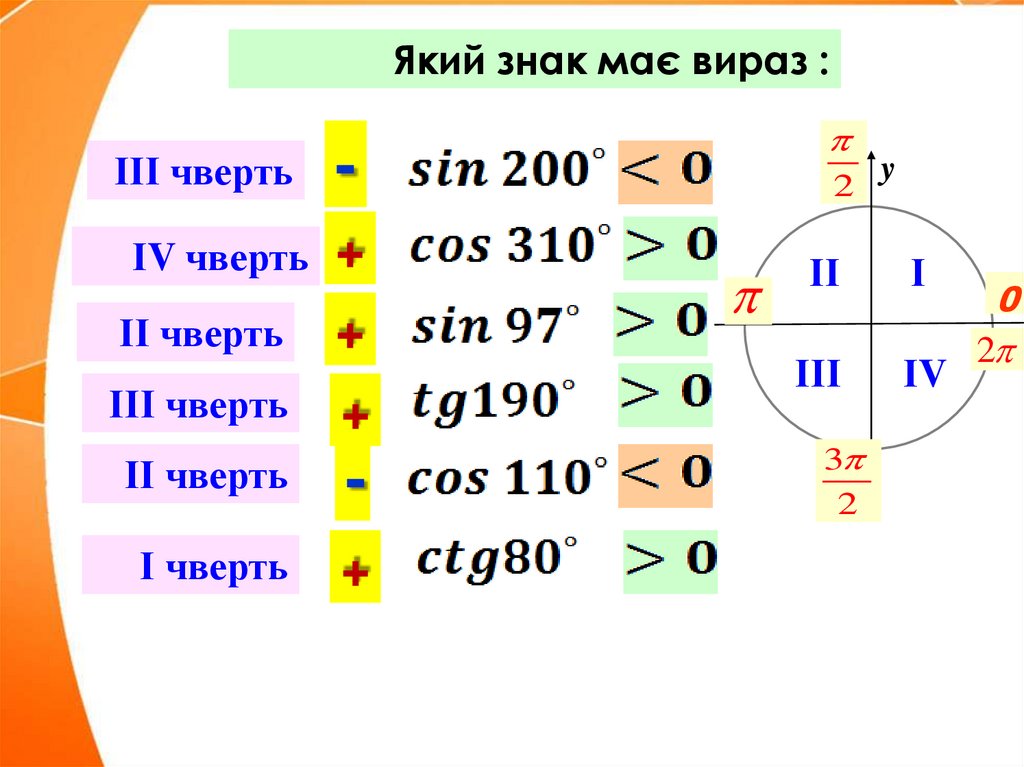
22.

Який знак має вираз :
ІІІ чверть
-
ІV чверть +
ІІ чверть
+
ІІІ чверть
+
ІІ чверть
-
І чверть
+
2
y
ІІ
І
ІІІ
ІV
3
2
0
2