Лекції 9-11 Тригонометричні функції числового аргументу

1.

Тригонометричні
функції
числового аргументу

2. Радіанна та градусна міри кутів

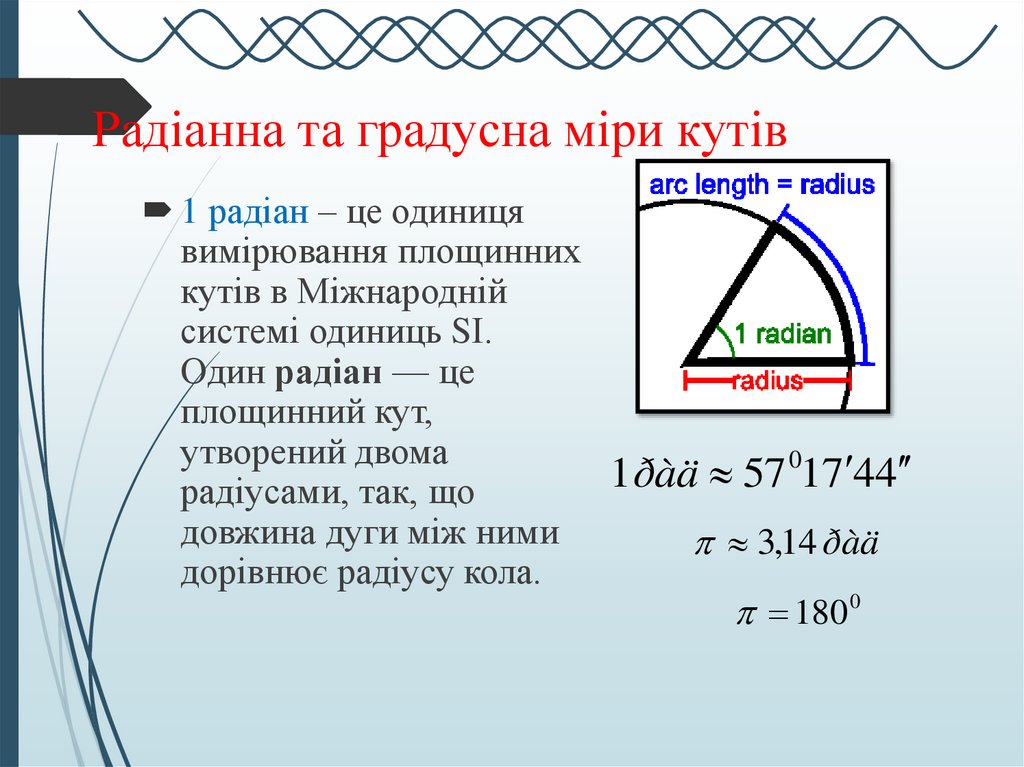
1 радіан – це одиниця
вимірювання площинних
кутів в Міжнародній
системі одиниць SІ.
Один радіан — це
площинний кут,
утворений двома
0
1
ðàä
57
17 44
радіусами, так, що
довжина дуги між ними
3,14 ðàä
дорівнює радіусу кола.
180 0

3.

4.

5.

6.

7.

8. Радіанна та градусна міри кутів

0
0
n
n
0
180
180
90 0
2
2
180
60 0
3
3
180 0
45 0
4
4
180 0
30 0
6
6
0
0
120 0
120
180 0
0
2
3
0
135
0
3
135
180 0
4

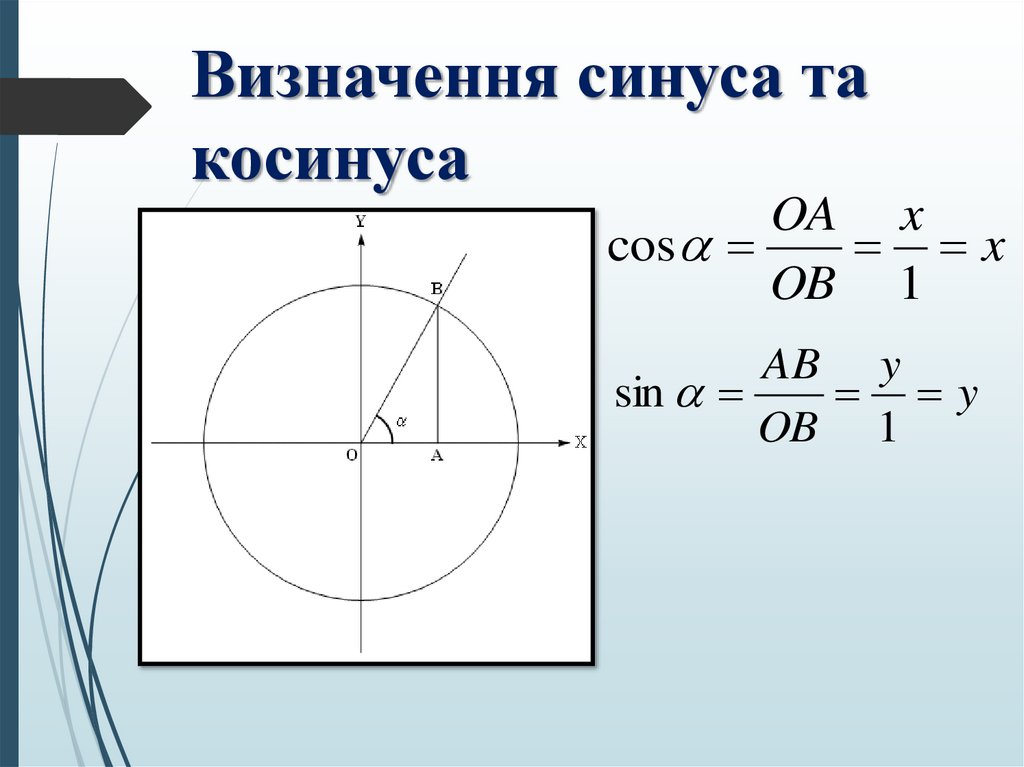
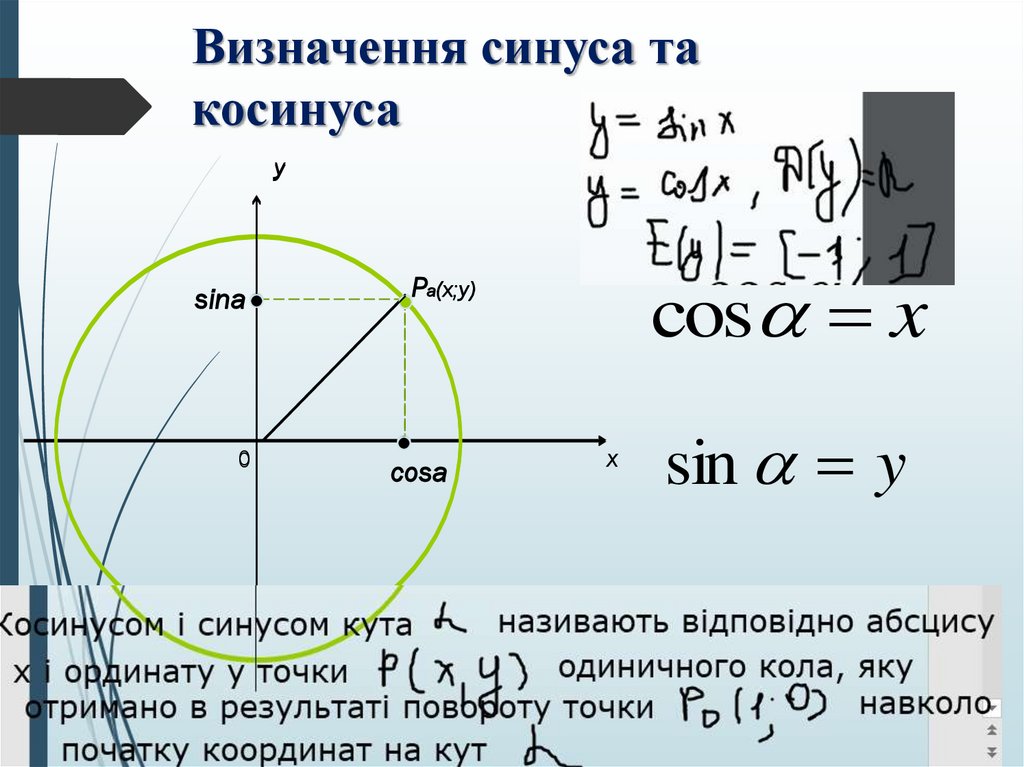
9. Визначення синуса та косинуса

OA x
cos
x
OB 1
AB y
sin
y
OB 1

10. Визначення синуса та косинуса

y
sinа
0
cos x
Pа(x;y)
cosа
x
sin y

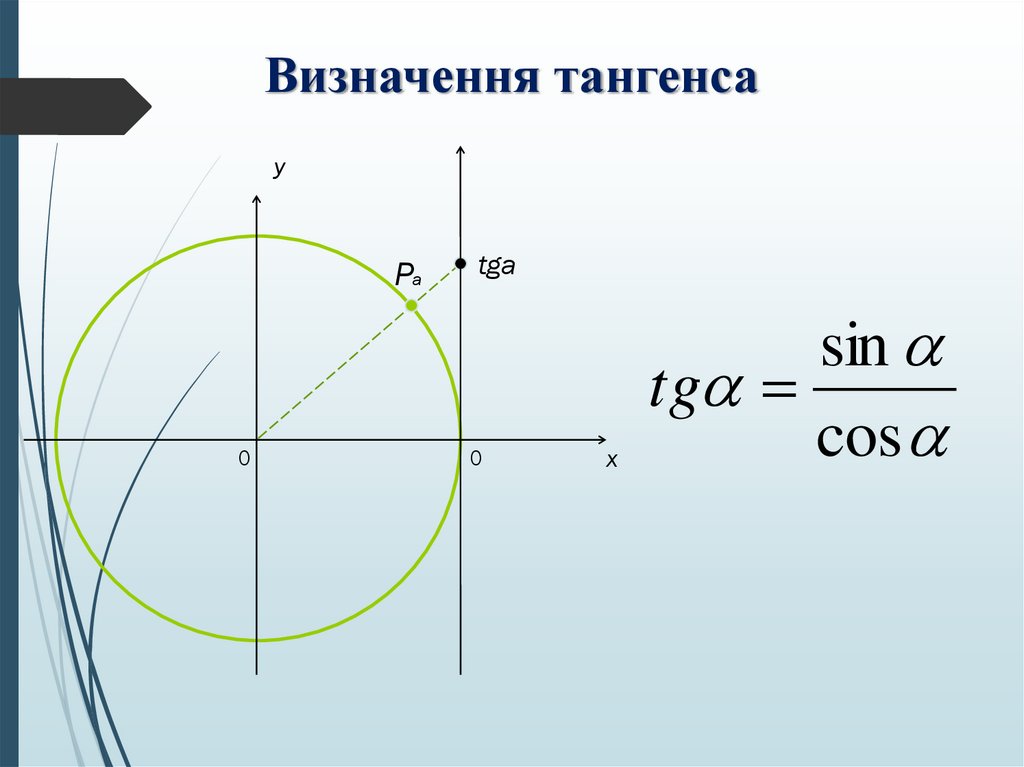
11. Визначення тангенса

y
Pa
0
tga
0
x
sin
tg
cos

12.

Визначення котангенса
y
ctga
0
Pa
0
x
cos
ctg
sin

13.

03 жовтня
Основні співвідношення між
тригонометричними функціями
одного аргументу

14.

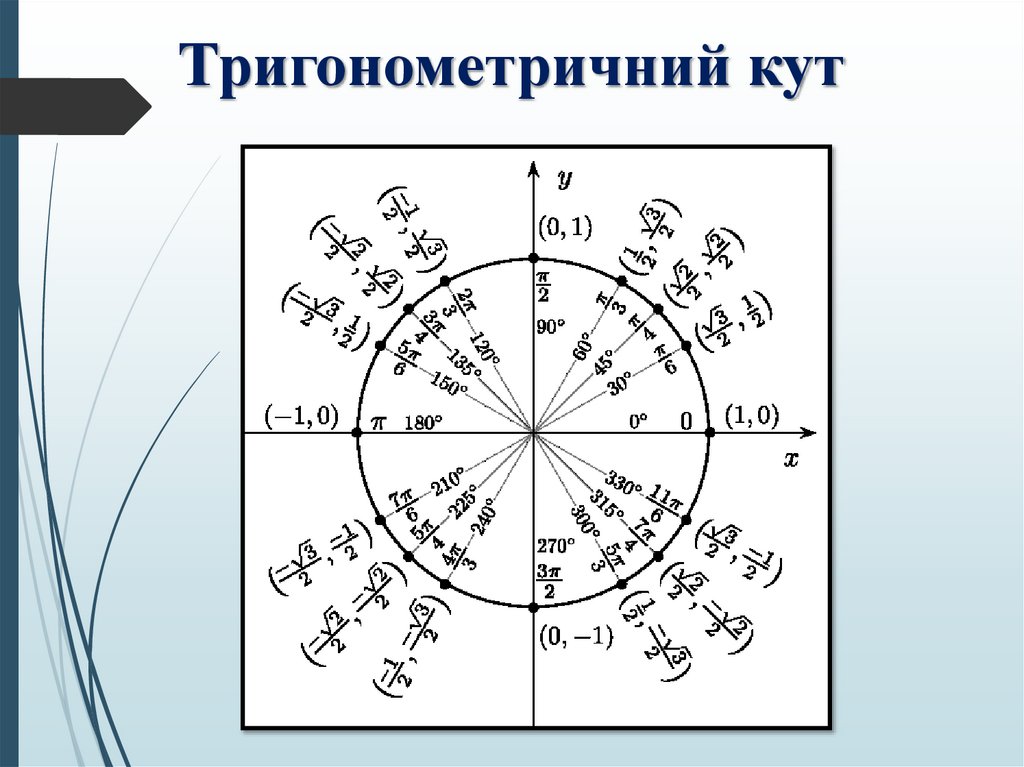
Тригонометричний кут

15. Графічний диктант

1. Кут 390 -кут ___ чверті;
2. tg(-110 )____0;
3. Обчислити
2 sin
6
2 cos
;
3
4. Відомо, що sin та cos від’ємні. Чи може
кут α бути кутом IV чверті?
5. Відомо, cosβ<0, а ctgβ>0. Кутом якої
чверті є кут β?
3
0
sin 750
6. Чи правильно, що
2
?

16.

y
0
0
x

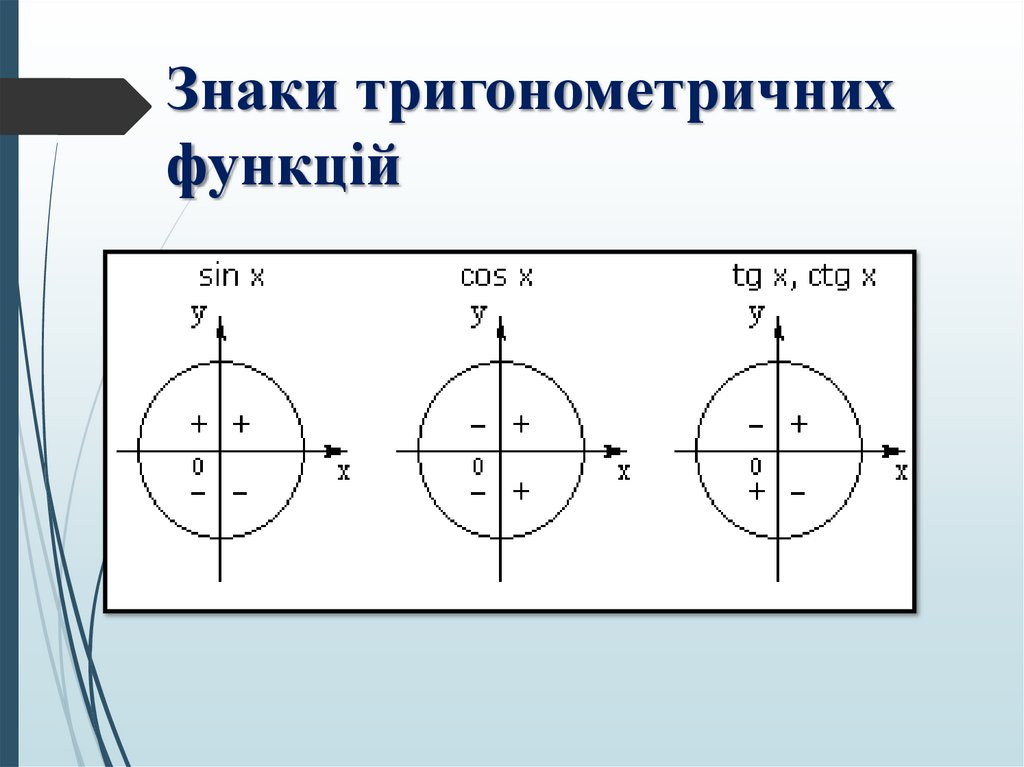
17. Знаки тригонометричних функцій

18.

Основна тригонометрична
тотожність
sin cos 1
2
2
sin 2 1 cos 2
sin 1 cos 2
cos 2 1 sin 2
cos 1 sin 2

19.

Зв’язок між тригонометричними
функціями одного аргументу
tg ctg 1
tg
ñtg
1
ctg
1
tg
1
2
1
tg
2
cos
1
2
1 ctg
2
sin

20.

Парність тригонометричних
функцій
sin sin
cos cos
tg tg
ctg ctg

21. Періодичність тригонометричних функцій

sin 2 n sin
cos 2 n cos
tg n tg
ctg n ctg

22.

23.

Домашнє завдання:
Виконати тест за посиланням:
https://vseosvita.ua/test/start/ykj496