Синус, косинус, тангенс, радіанне вимірювання кутів

1. “Синус, косинус, тангенс, радіанне вимірювання кутів”

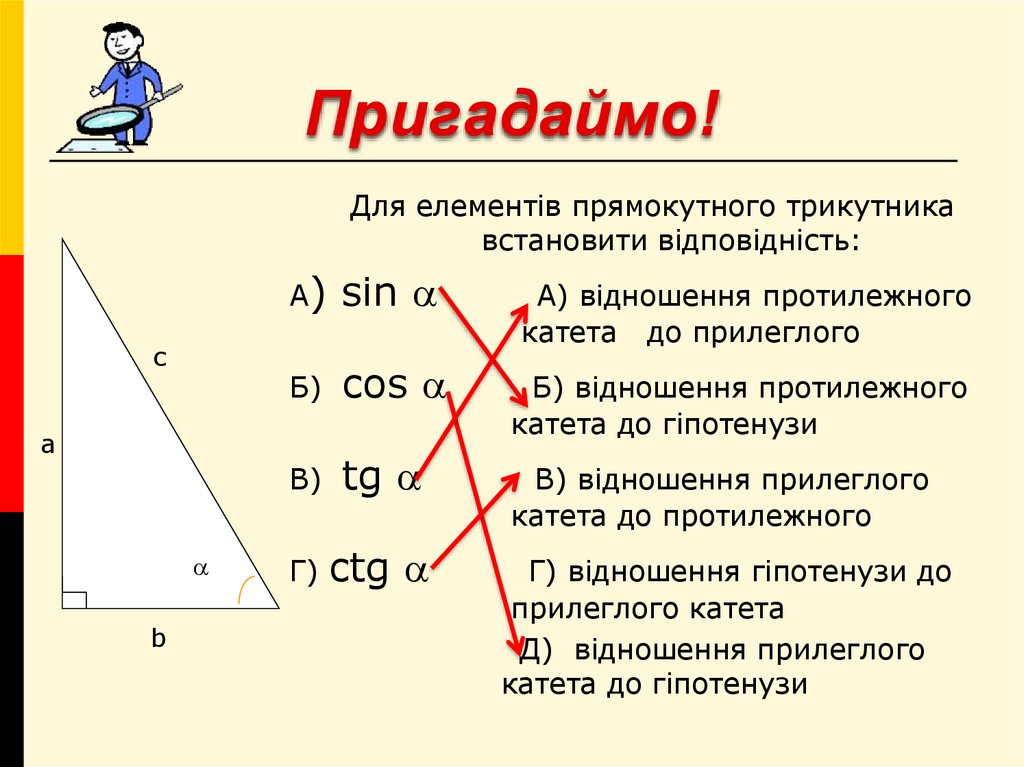
2. Пригадаймо!

Для елементів прямокутного трикутника
встановити відповідність:
с
А) sin
А) відношення протилежного
катета до прилеглого
Б)
cos
Б) відношення протилежного
катета до гіпотенузи
В)
tg
В) відношення прилеглого
катета до протилежного
a
b
Г) ctg
Г) відношення гіпотенузи до
прилеглого катета
Д) відношення прилеглого
катета до гіпотенузи

3.

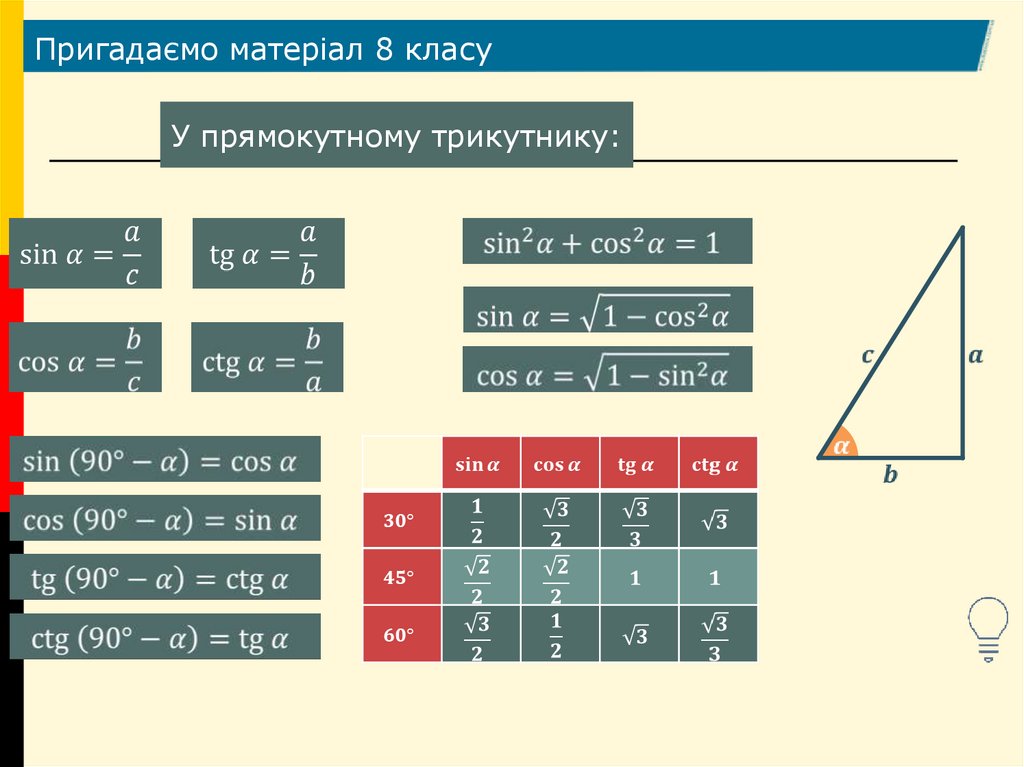
Пригадаємо матеріал 8 класу
У прямокутному трикутнику:

4.

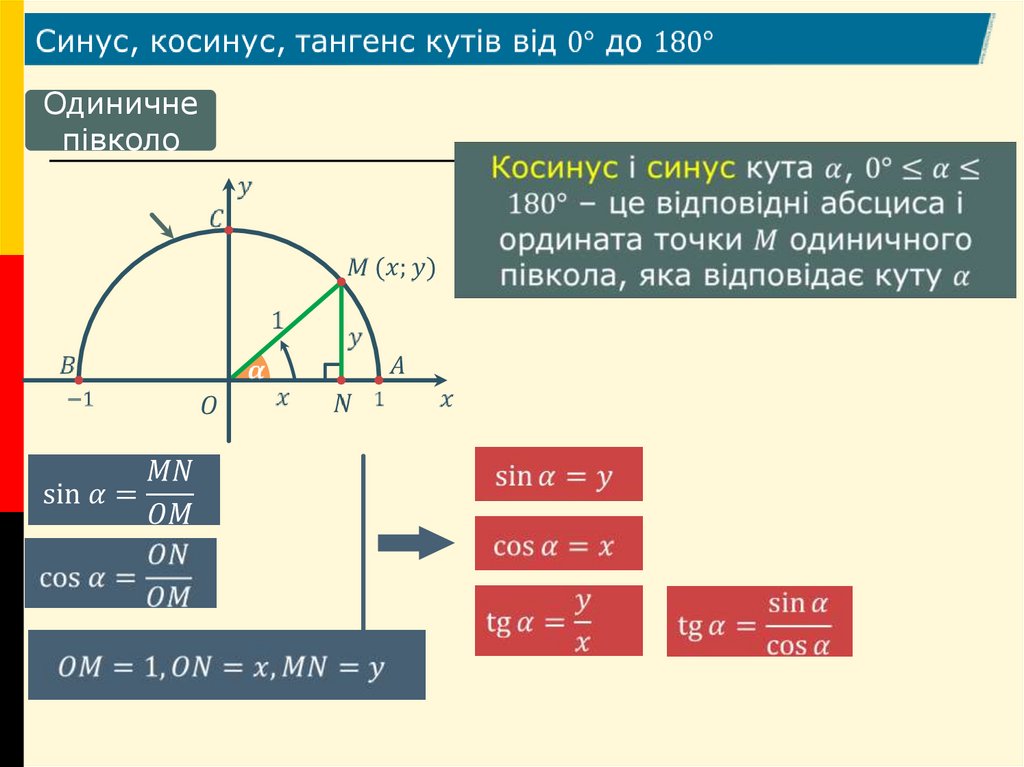
Одиничне
півколо

5.

не
існує

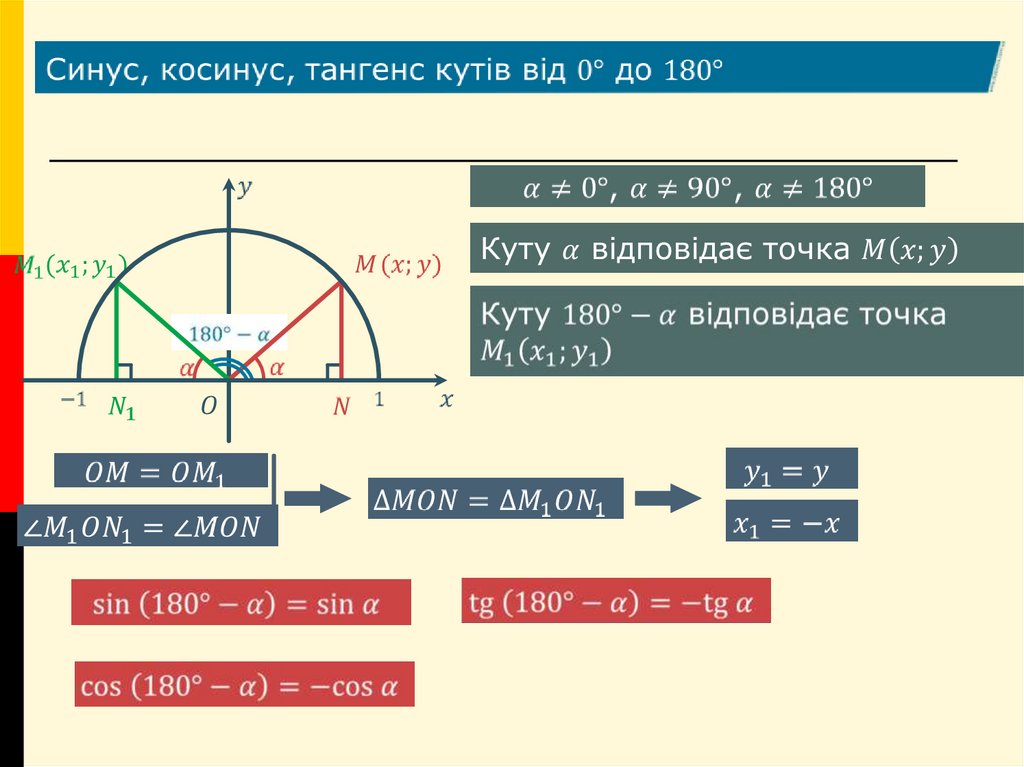
6.

7.

Основна тригонометрична тотожність
Відомо з 8 класу
не
існує

8. Пригадаймо!

Коло – це геометрична фігура, яка
складається з усіх точок площини,
розміщених на даній відстані від даної
точки (центр кола)

9. Пригадаймо!

Радіус кола – це відрізок, що
сполучає центр кола з якою-небудь
його точкою.
O
R

10. Пригадаймо!

Кут - це два промені, що виходять з
однієї точки

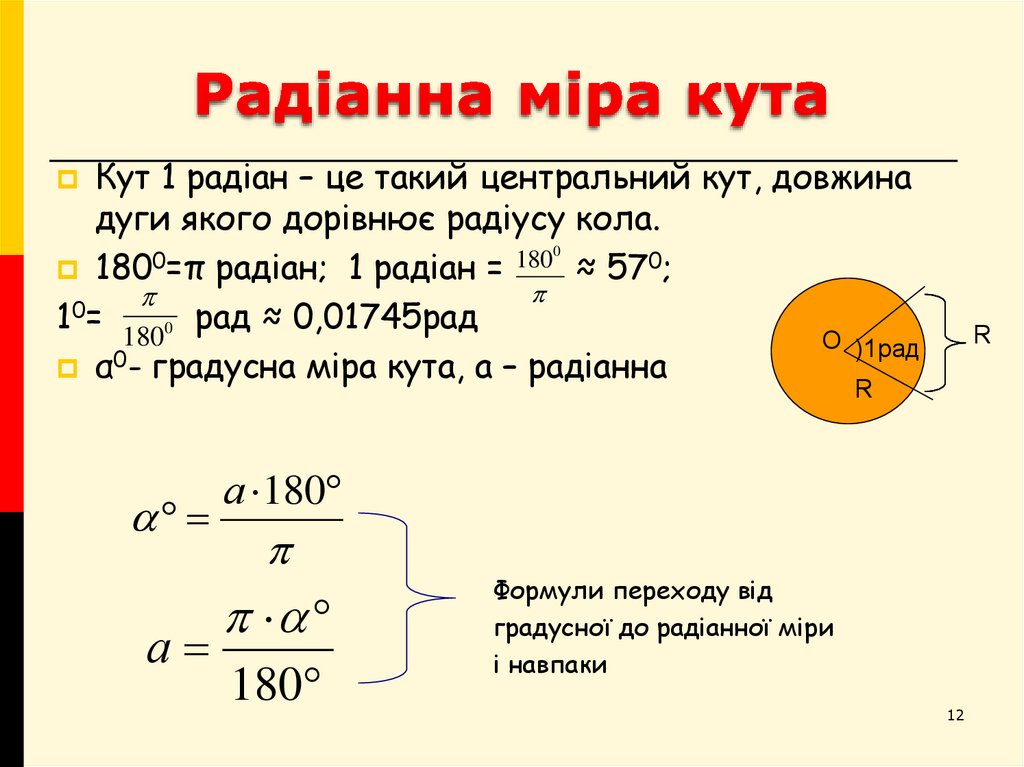
11. Радіанна міра кута

У математиці, астрономії, фізиці
використовують радіанну міру
вимірювання кутів. Перше
видання яке містило термін
“радіан”, вийшло в 1873 р в
Англії.
“Радіан” походить від
латинського radian (спиця,
промінь).

12. Радіанна міра кута

Кут 1 радіан – це такий центральний кут, довжина
дуги якого дорівнює радіусу кола.
0
180
0
180 =π радіан; 1 радіан =
≈ 570;
0
1 =
рад ≈ 0,01745рад
1800
α0- градусна міра кута, а – радіанна
а
R
О )1рад
R
а 180
180
Формули переходу від
градусної до радіанної міри
і навпаки
12

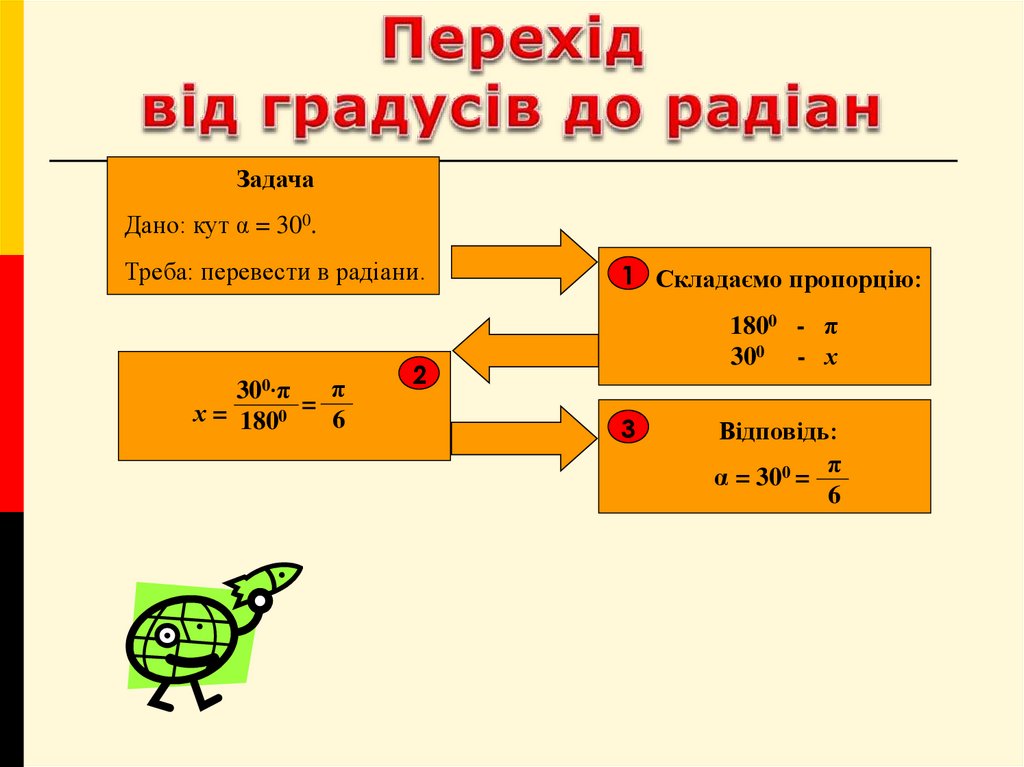
13. Перехід від градусів до радіан

Задача
Дано: кут α = 300.
Треба: перевести в радіани.
π
300∙π
=
х = 1800
6
1 Складаємо пропорцію:
1800 - π
300 - х
2
3
Відповідь:
π
α = 300 =
6

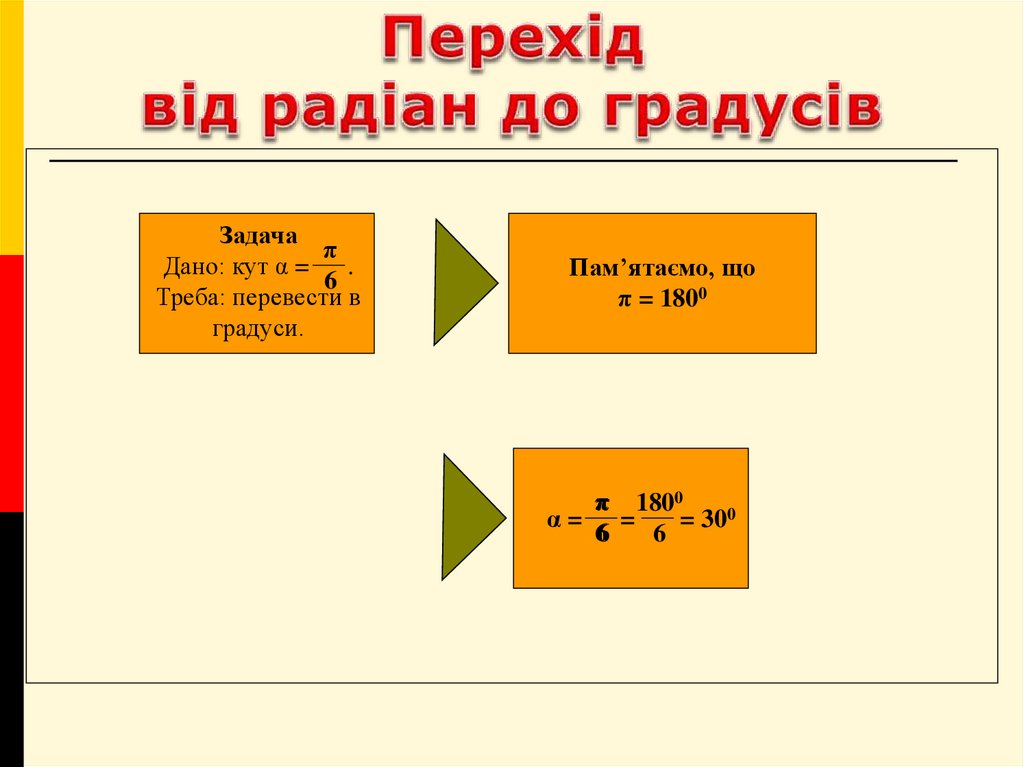
14. Перехід від радіан до градусів

Задача
π
Дано: кут α =
.
6
Треба: перевести в
градуси.
Пам’ятаємо, що
π = 1800
π 1800
α= =
= 300
6
6

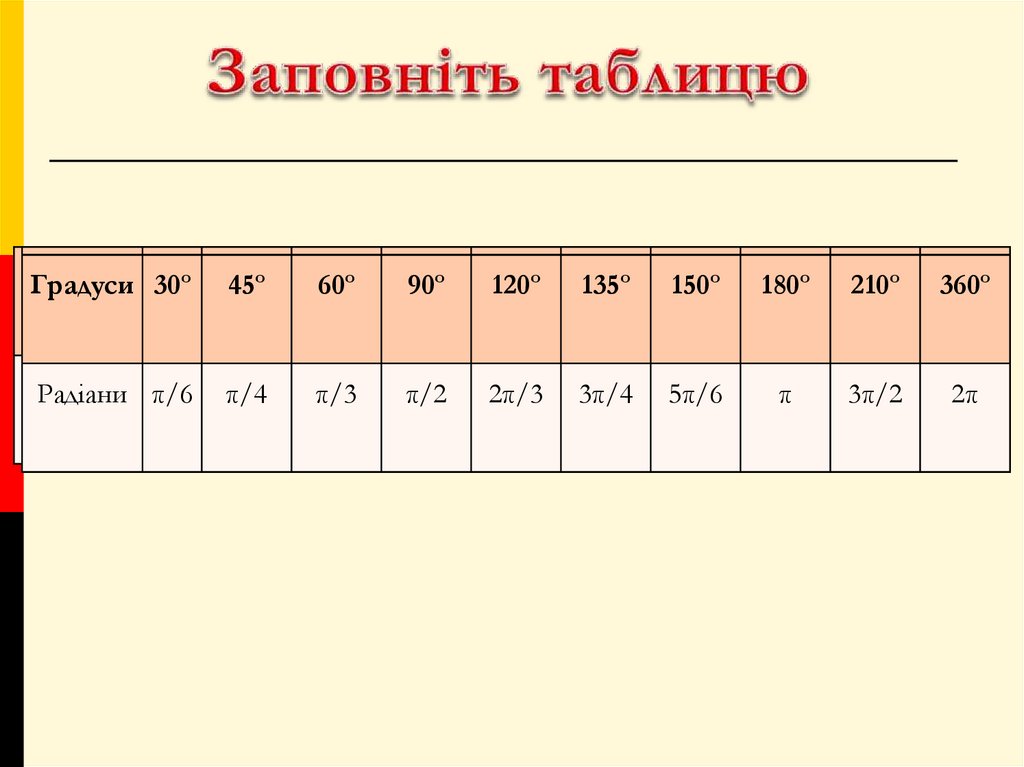
15. Заповніть таблицю

Градуси
Градуси
30º
Градуси 30º
30º
45º
45º
45º
60º
60º
90º
90º
120º
120º
135º
135º
150º
180º
180º
210º
360º
360º
Радіани
Радіани
π/6
π/4
Радіани π/6
π/6 π/4
π/4
π/3
π/3
π/2
π/2
2π/3
2π/3
3π/4
3π/4
5π/6
5π/6
π
3π/2
3π/2
2π