Радіанне вимірювання кутів. Графіки тригонометричних функцій і їх властивості

1. “Радіанне вимірювання кутів. Графіки тригонометричних функцій і їх властивості.”

2. Радіанна міра кута

У математиці, астрономії, фізиці
використовують радіанну міру
вимірювання кутів. Перше
видання яке містило термін
“радіан”, вийшло в 1873 р в
Англії.
“Радіан” походить від
латинського radian (спиця,
промінь).

3. Радіанна міра кута

Кут 1 радіан – це такий центральний кут, довжина
дуги якого дорівнює радіусу кола.
0
180
1800=π радіан; 1 радіан =
≈ 570;
0
1 =
рад ≈ 0,01745рад
0
180
R
О )1рад
R
α0- градусна міра кута, а – радіанна
а
а 180
180
Формули переходу від
градусної до радіанної міри
і навпаки
3

4.

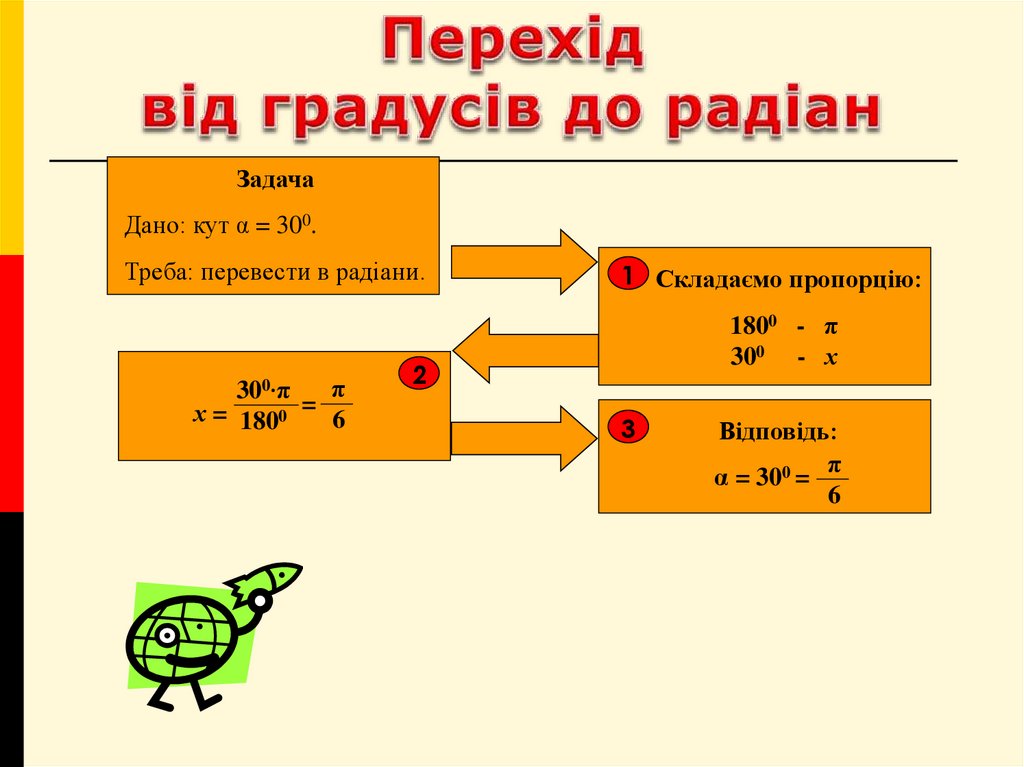
5. Перехід від градусів до радіан

Задача
Дано: кут α = 300.
Треба: перевести в радіани.
π
300∙π
=
х = 1800
6
1 Складаємо пропорцію:
1800 - π
300 - х
2
3
Відповідь:
π
α = 300 =
6

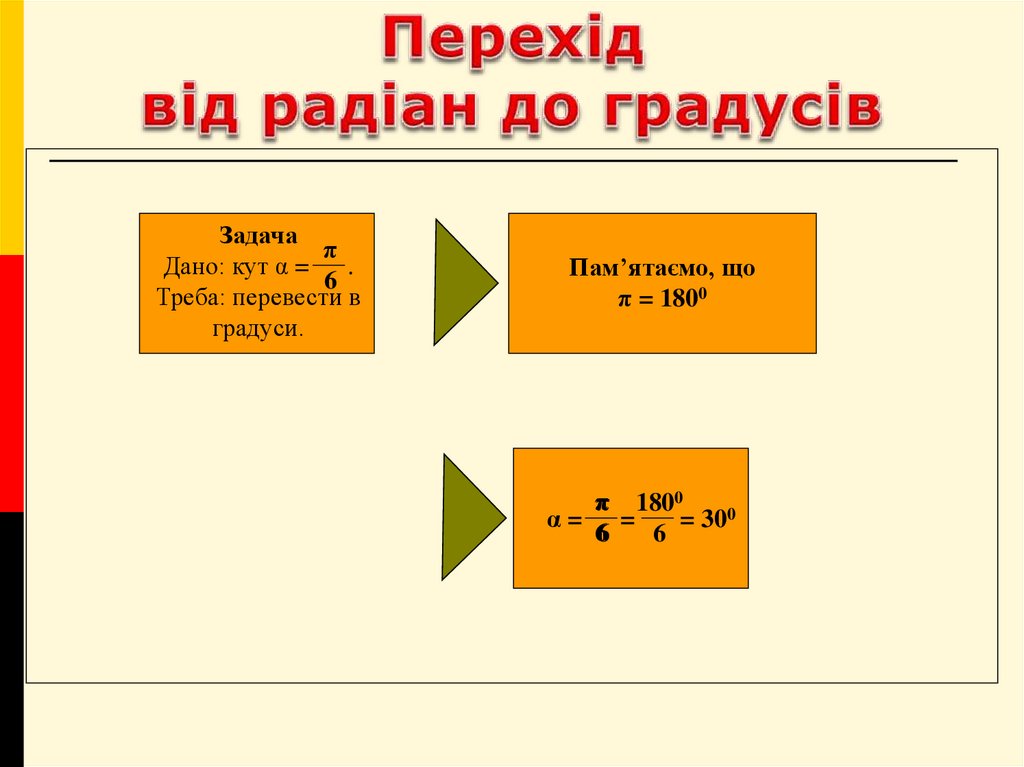
6. Перехід від радіан до градусів

Задача
π
Дано: кут α =
.
6
Треба: перевести в
градуси.
Пам’ятаємо, що
π = 1800
π 1800
α= =
= 300
6
6

7.

Виконати завдання
на с.80 підручника

8. Заповніть таблицю

Градуси
Градуси
30º
Градуси 30º
30º
45º
45º
45º
60º
60º
90º
90º
120º
120º
135º
135º
150º
180º
180º
210º
360º
360º
Радіани
Радіани
π/6
π/4
Радіани π/6
π/6 π/4
π/4
π/3
π/3
π/2
π/2
2π/3
2π/3
3π/4
3π/4
5π/6
5π/6
π
3π/2
3π/2
2π
l – довжина дуги;
α – кут в радіанах(радіанна міра дуги);
R – радіус

9.

10.

11.

Одиничне коло
№8.6; 8.8; 8,10; 8.12.

12.

13.

14.

15.

16.

17. Домашнє завдання

За підручником О.С.Істер
Математика 10кл
§ 8. Радіанна міра кутів, с.77-80;
§11 с.102-105; §12 с.109-117.
№ № 8.2, 8.4, 8.6, 8.10, 8.11, 8.15
с.80-81;
11.4, 11.6, 11.8 с.106;
12.2 с.118