Similar presentations:
лекция 7_НСВ_основные характеристики
1. Теория вероятностей и математическая статистика
7. НЕПРЕРЫВНЫЕСЛУЧАЙНЫЕ ВЕЛИЧИНЫ
2. НЕПРЕРЫВНАЯ СЛУЧАЙНАЯ ВЕЛИЧИНА (НСВ)
• - это случайная величина, которая можетпринимать любое значение из некоторого
конечного или бесконечного промежутка.
• Случайная величина Х называется непрерывной,
если ее функция распределения F(x) непрерывна
в любой точке х числовой оси.
• Функция распределения F(x) непрерывной
случайной величины обладает всеми свойствами,
которые справедливы для дискретной величины.
3. Функция распределения
повторимФункция распределения
• Функцией распределения случайной величины
Х называется функция F(x), значение которой для
любого действительного числа х равно
вероятности события «X<x», то есть вероятность
того, что случайная величина Х принимает
значения меньшие х: F(x)=P(X<x).
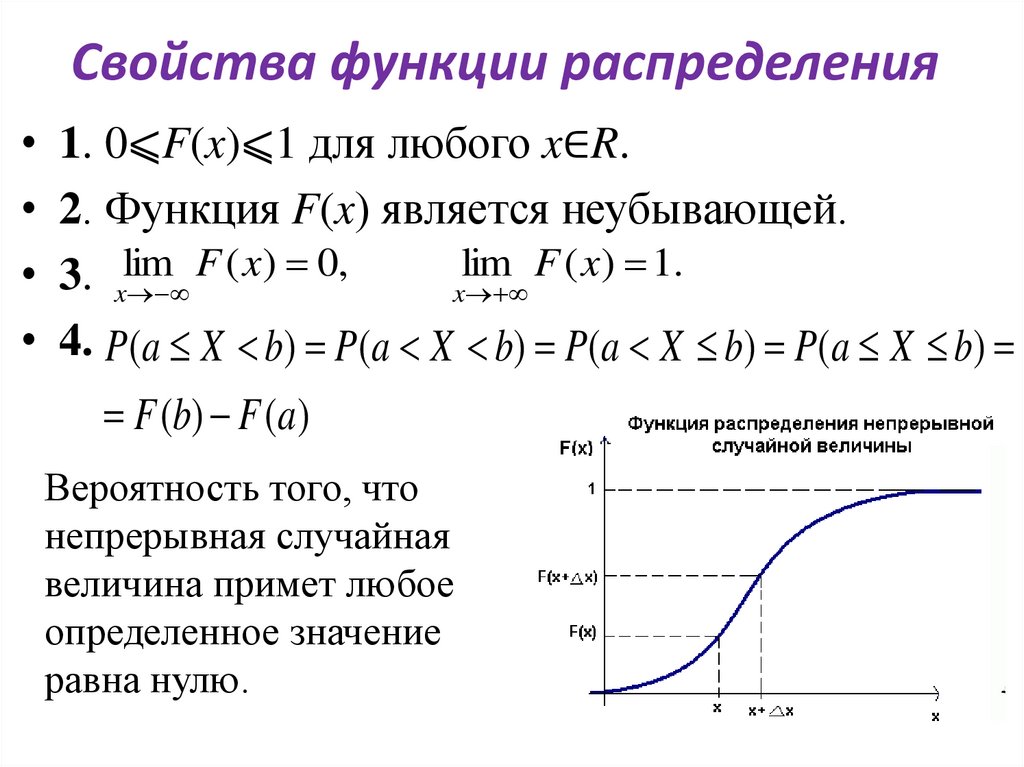
Свойства функции распределения
• 1. 0⩽F(x)⩽1 для любого x∈R.
• 2. Функция F(x) является неубывающей.
F ( x) 0,
lim F ( x) 1.
• 3. xlim
x
• 4. P(a⩽X<b)=F(b) – F(a)
• 5. Функция F(x) непрерывна слева в любой точке.
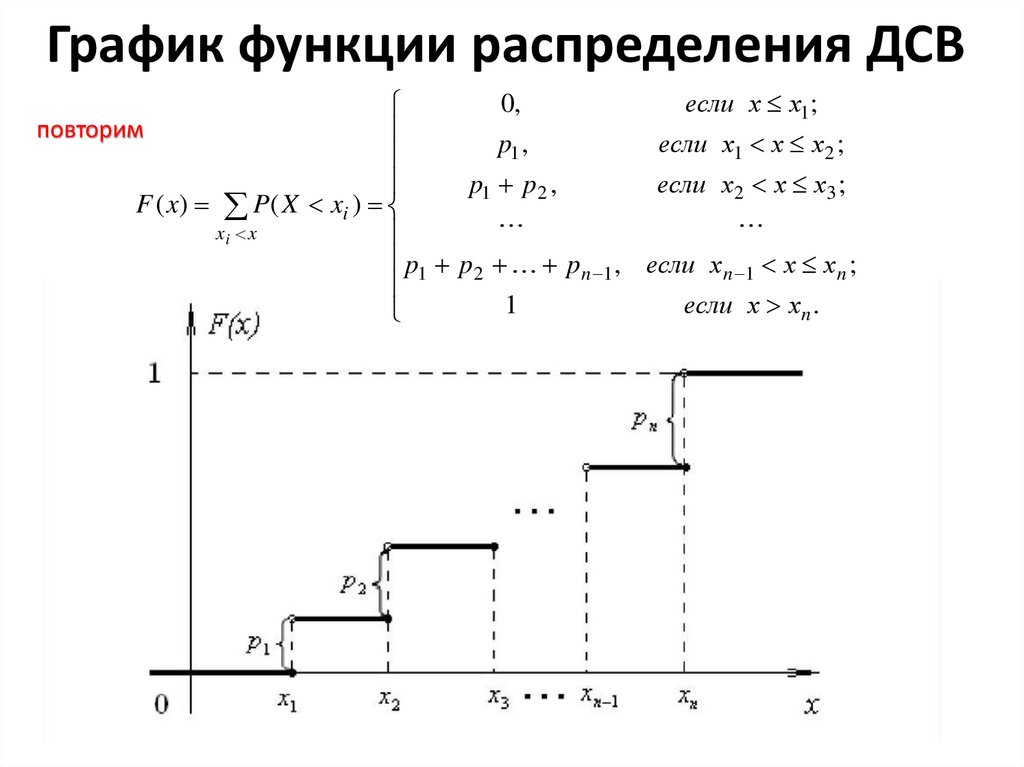
4. График функции распределения ДСВ
0,если х х1 ;
повторим
p1 ,
если х1 х х2 ;
p1 p2 ,
если х2 х х3 ;
F ( x) P( X xi )
xi x
p1 p2 pn 1 , если хn 1 х хn ;
1
если х хn .
5.
Свойства функции распределения• 1. 0⩽F(x)⩽1 для любого x∈R.
• 2. Функция F(x) является неубывающей.
F ( x) 0,
lim F ( x) 1.
• 3. xlim
x
• 4. P(a X b) P(a X b) P(a X b) P(a X b)
F (b) F (a)
Вероятность того, что
непрерывная случайная
величина примет любое
определенное значение
равна нулю.
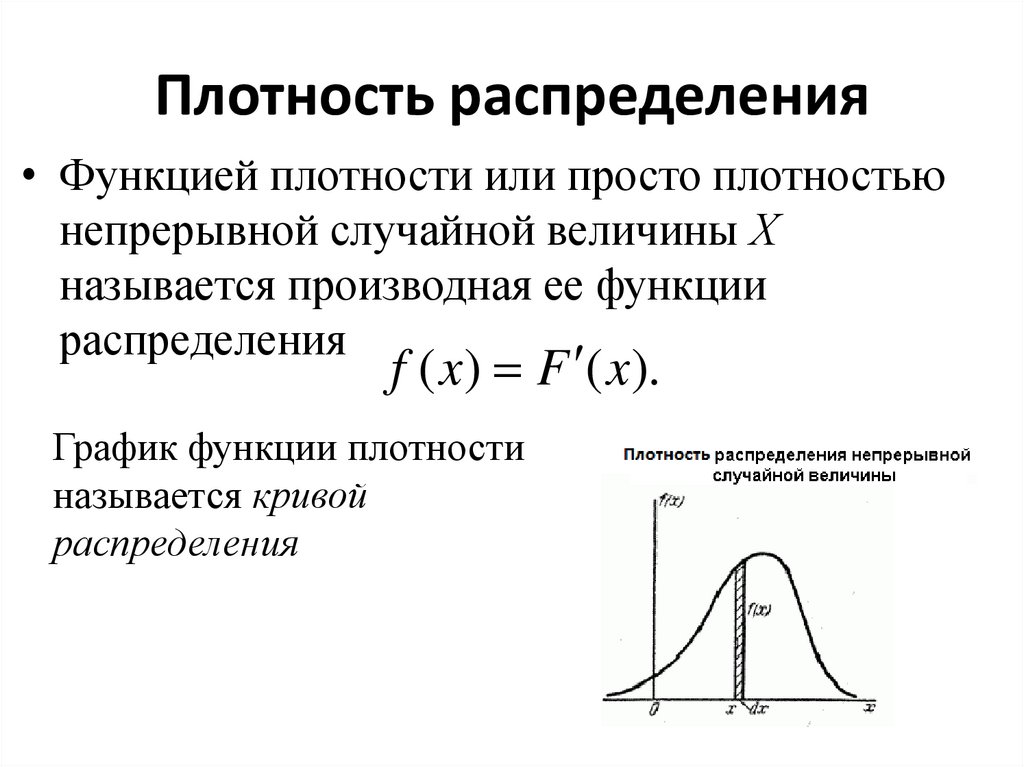
6. Плотность распределения
• Функцией плотности или просто плотностьюнепрерывной случайной величины Х
называется производная ее функции
распределения
f ( x) F ( x).
График функции плотности
называется кривой
распределения
7. Свойства функции плотности
f ( x) F ( x).f ( x) 0.
• 1)
f ( x)dx 1.
• 2)
x
• 3)
F ( x) f (t )dt.
b
• 4) P(a X b) f ( x)dx.
a
f(x)
f(x)
f(x)
b
S=1
S= f (x)dx
S=F(x)
a
0
x
0
x
a 0
b
x
8. Основные числовые характеристики СВ
• Математическое ожиданиеM ( X ) xi pi .
i 1
M ( X ) x f ( x)dx.
• Дисперсия D( X ) M ( X M ( X ))
2
D( Х ) M ( X 2 ) M 2 ( X )
n
D( X ) xi M ( X ) pi xi2 pi ( MX ) 2
2
i 1
i 1
DX ( x MX ) 2 f ( x)dx.
n
DX x 2 f ( x)dx ( MX ) 2
• Среднее квадратическое отклонение
X D(X )
9.
• Непрерывная случайная величина задана функциейраспределения. Найти функцию плотности и вычислить
числовые характеристики случайной величины:
f ( x) F ( x).
x 0,
0,
1 2
F ( x) x , 0 x 3,
9
x 3.
1,
x 0,
0 ,
x 0,
0,
1
f ( x) F ( x) x 2 , 0 x 3, 2 x, 0 x 3,
9
9
x 3
x 3
(1) ,
0,
0, х (0;3],
f ( x) 2
x, x (0;3].
9
10.
x 0,0,
1
F ( x) x 2 , 0 x 3,
9
x 3.
1,
0, х (0;3],
f ( x) 2
x, x (0;3].
9
M ( X ) x f ( x)dx.
3
3 3
3
2
2 x
2 2
M ( X ) x x dx x dx
9
9 3
9
0
0
2
3
3
(
3
0
) 2
9 3
0
DX x 2 f ( x)dx ( MX ) 2
3
3
4 3
2
M ( X 2 ) x 2 x dx 2 x 3dx 2 x 2 (34 0 4 ) 4,5
9
9
9 4 0 9 4
0
0
DX M ( X 2 ) ( MX ) 2 4,5 2 2 0,5.
11.
x 0,0,
1 2
F ( x) x , 0 x 3,
9
x 3.
1,
0, х (0;3],
f ( x) 2
x, x (0;3].
9
1
2
1
1
P(0 X 1) f ( x)dx F (1) F (0)
0
9 2 9
12.
• Найти значение параметра а и функциюраспределения при известной плотности
распределения:
если 0 x 2;
ax,
f ( x)
0, если x 0 или x 2.
• Вычислить вероятность попадания случайной
величины на отрезок [ 1;1.
f ( x)dx 1.
2
f ( x)dx axdx 1
0
ax
2
2 2
1
0
а
1
2
2
( 2 0 ) 1 2a 1 a
2
2
x
, если 0 x 2;
f ( x) 2
0, если x 0 или x 2.
x
F ( x) f (t )dt.
13.
• Найти значение функцию распределения приизвестной плотности распределения:
x
, если 0 x 2;
f ( x) 2
0, если x 0 или x 2.
x 0
x 2
F ( x) f (t )dt.
x
F ( x) 0 dt 0
0 x 2
x
0
x
x
x
2
2
t
t
x
F ( x) f (t )dt 0 dt dt 0
2
40 4
0
x
0
2
x
2
2
2
t
t
2
F ( x) f (t )dt 0 dt dt 0 dt 0
0 1
2
40
4
0
2
0, если x 0;
x 2
F ( x) , если 0 x 2;
4
1, если x 2.
14.
• Вычислить вероятность попадания случайнойвеличины на отрезок [ 1;1]
0, если x 0;
x 2
F ( x) , если 0 x 2;
4
1, если x 2.
P( 1 X 1) F (1) F ( 1)
1
0
1
2
1
1
0
4
4
2 1
x
1 x
1 2
1
2
P( 1 X 1) f ( x)dx 0dx dx 0
(1 0 ) .
2 2 0 4
4
1
1
02
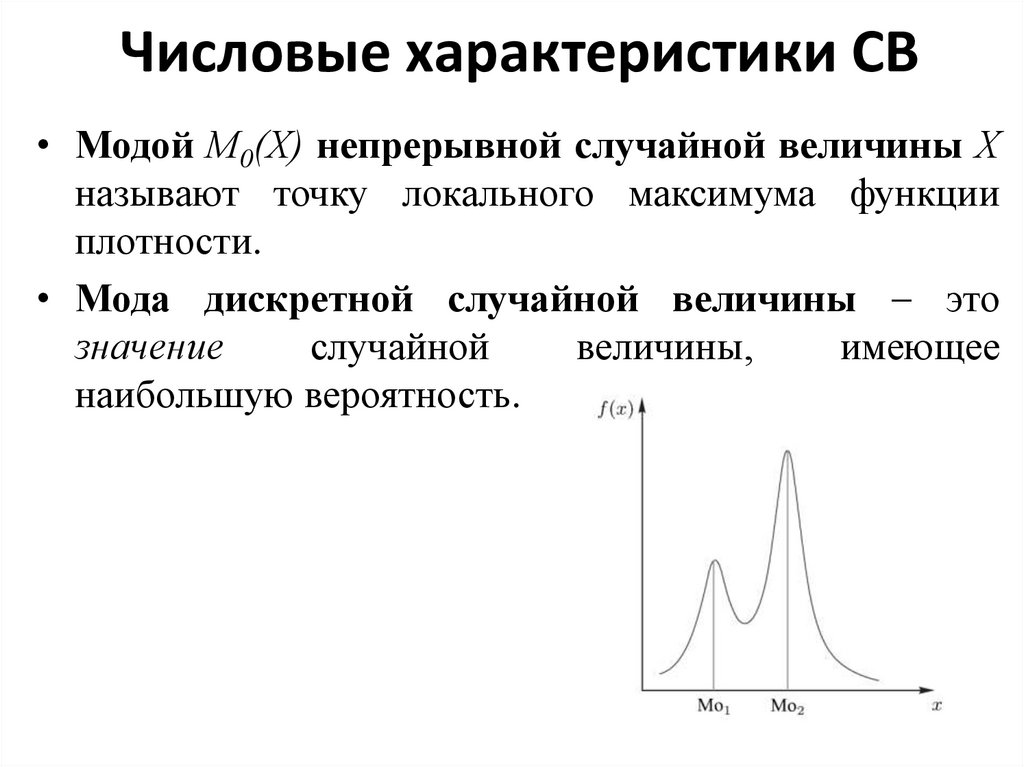
15. Числовые характеристики СВ
• Модой М0(Х) непрерывной случайной величины Хназывают точку локального максимума функции
плотности.
• Мода дискретной случайной величины это
значение
случайной
величины,
имеющее
наибольшую вероятность.
16. Числовые характеристики СВ
• Коэффициент вариации V(X) :V (Х )
X
MX
100%
• Он показывает степень изменчивости по отношению
к среднему значению.
1 X 2 X
1 X
V1 ( Х )
100%
M (X )
M1( X ) M 2 ( X )
X
V1 ( Х )
100%
M1( X )
2X
100%
M (X )
V2 ( Х )
X
V2 ( Х )
100%
M2(X )
Вариация - многообразие, колеблемость, изменяемость величины
признака у отдельных единиц совокупности






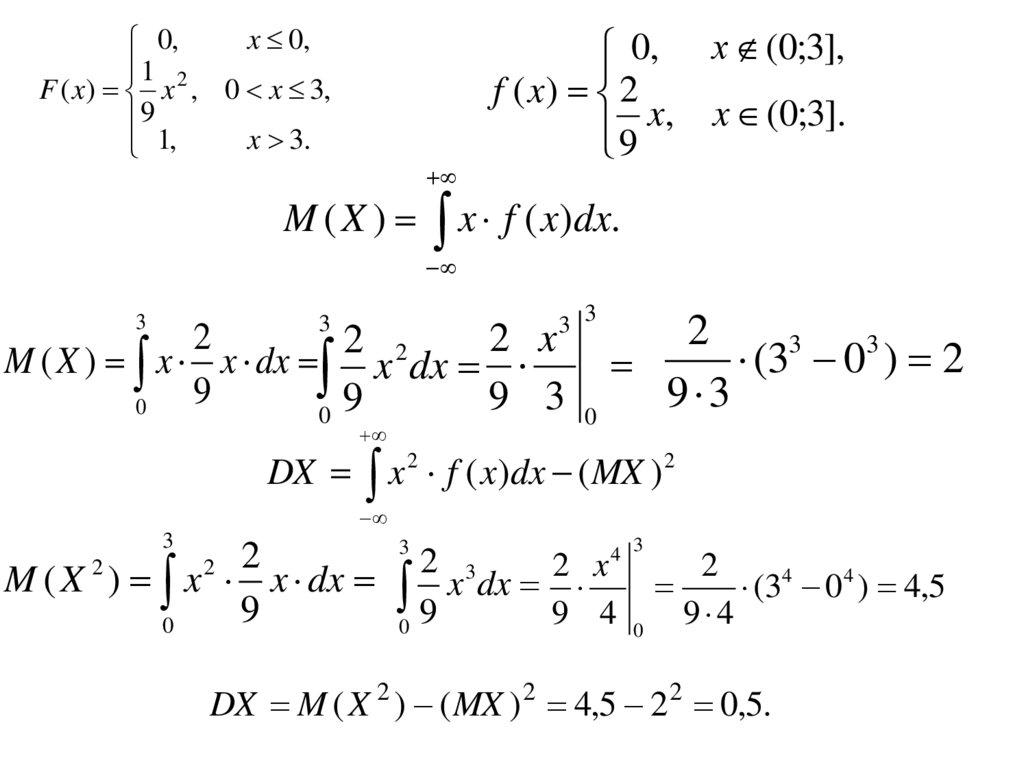
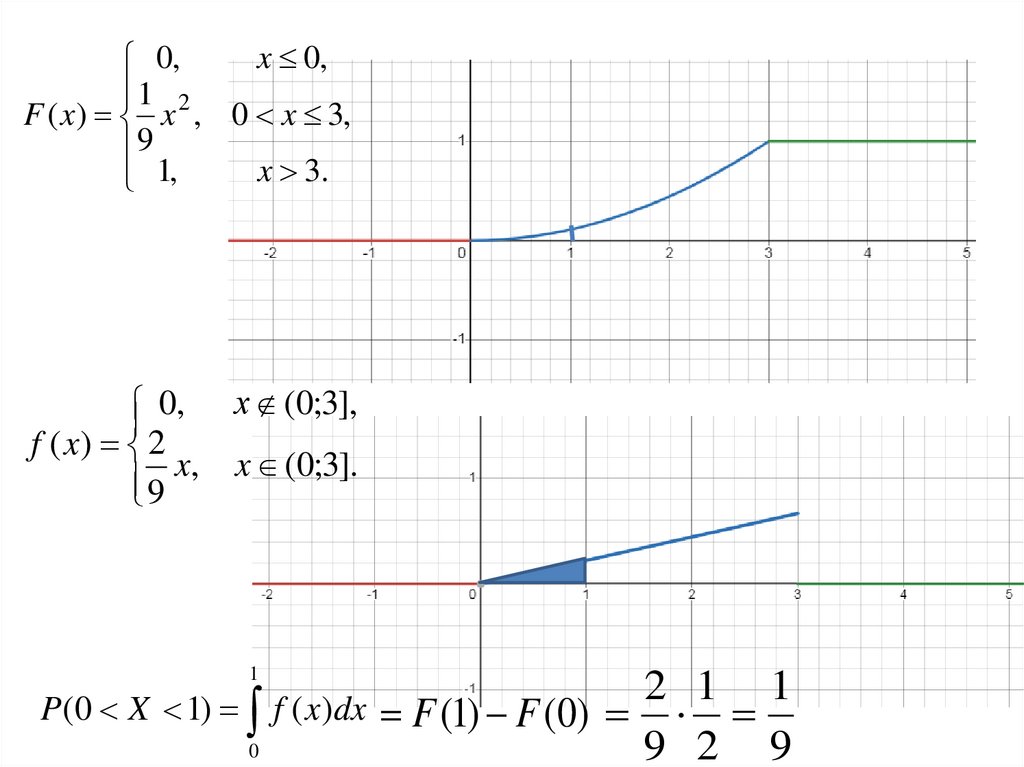




 mathematics
mathematics