Similar presentations:
Типовые законы распределения
1.
Типовые законы распределенияИндикатор случайного события А – это дискретная случайная
величина X, которая равна 1 при осуществлении события А и 0 при
осуществлении А:
1 , A
X
0 , A
Ряд распределения вероятностей индикатора случайного события:
xi
0
1
pi
q
p
где p – вероятность осуществления А;
q =1-p – вероятность осуществления А.
Числовые характеристики индикатора случайного события:
mX p, DX qp
(6.1)
2.
Геометрическое распределение имеет дискретная случайная величина Х,если она принимает значения 0, 1, … , с вероятностями:
p ( X i ) pi q p
i
(6.2)
где p – параметр распределения (0 ≤ p ≤1), q=1-p.
Числовые характеристики геометрического распределения:
2
X
X
(6.3)
m q / p, D q / p
Биномиальное распределение имеет дискретная случайная величина X,
если она принимает значения 0, 1, … , n со следующими вероятностями:
n!
p( X i) pi
p i q n i
i !(n i)!
где
n, p – параметры распределения (0 ≤ p ≤1), q=1 - p.
(6.4)
3.
Числовые характеристики биномиального распределения:mX np, DX nqp
(6.5)
Распределение Пуассона имеет дискретная случайная
величина Х, если она принимает значения 0, 1, … , со
следующими вероятностями:
i
a (6.6)
i
a
p( X i ) p e
i!
где a – параметр распределения (a >0 ).
Числовые характеристики пуассоновской случайной величины:
mX a, DX a
(6.7)
4. Условия возникновения:
1.Данное распределение является предельным случаембиномиального, когда число опытов n →∞
(неограниченно увеличивается), а p →0 (вероятность
события в одном опыте стремится к 0) .
2. Физические условия возникновения.
Поток случайных событий- Рассмотрим
временную ось, на которой будем отмечать моменты
возникновения случайных событий
(например,
отказы компонентов в сложном техническом
устройстве, заявки на обслуживание).
Поток с.с. называется стационарным, если число
событий, приходящихся на интервал в общем случае
не зависит от расположения этого участка на
временной оси и определяется только его
длительностью, т.е. среднее число событий в единице
времени ( ) (интенсивность потока) постоянно.
5.
Поток с.с. называется ординарным, есливероятность попадания в некоторый участок t двух и
более с.с. значительно меньше, чем вероятность
попадания 1-го события.
В потоке отсутствует последействие, если
вероятность попадания событий на участок не
зависит от того, сколько событий попало на другие
участки, не пересекающиеся с данным.
Поток с.с. называется простейшим, или
Пуассоновским, если он является стационарным,
ординарным и без последействия. Для
Пуассоновского потока число событий поступивших
в течение интервала является дискретной с.с. с
распределением Пуассона с параметром а =
6.
ТИПОВЫЕ ЗАКОНЫ РАСПРЕДЕЛЕНИЯ Н.С.В.РАВНОМЕРНОЕ РАСПРЕДЕЛЕНИЕ
Н.С.В. Х равномерно распределена в интервале
а; b], если ее плотность вероятности в этом интервале
постоянна, т.е. если все значения в этом интервале
равновероятны.
Плотность вероятности:
c, a x b
f (x)
0 , x a , x b
Так как
1 / (b a), a x b
f (x )
0, x a, x b
b
a
1 f ( x )dx 0 cdx 0 c( b a )
7.
числовые характеристики:M(X )
a
b
a
b
x
dx
b
a
xp( x )dx xp(x )dx xp(x )dx xp(x )dx
2 b
1 x
b2 a 2 b a
b a 2 a 2( b a )
2
a
b
a
b
D( X ) ( x mx )2 f ( x)dx ( x mx )2 f ( x)dx ( x mx )2 f ( x)dx ( x mx )2 f ( x)dx
b
a b )3 (b a b )3 (a a b )3
(
x
2
(x mx )
(
b
a
)
1 (x mx
2
2
2
dx
b a
b a
3(b a)
12
3 a 3(b a)
a
b
)3
2
x
b
b a
2 3
a
8.
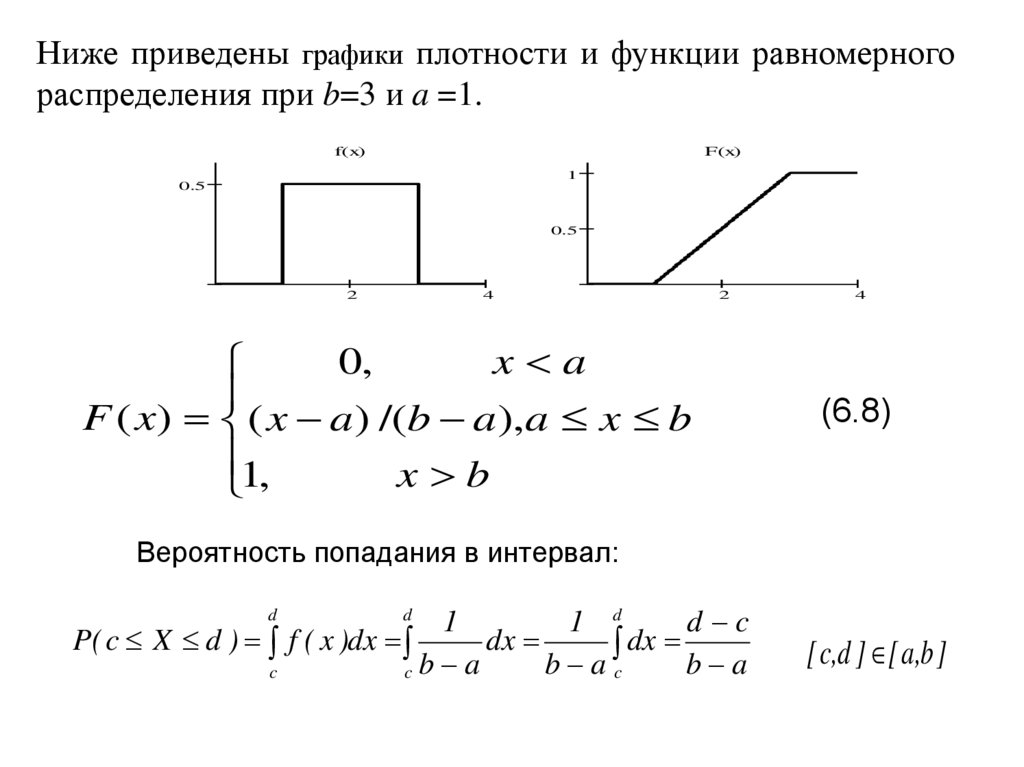
Ниже приведены графики плотности и функции равномерногораспределения при b=3 и a =1.
f(x)
F(x)
1
0.5
0.5
2
4
2
0,
x a
F ( x) ( x a) /(b a),a x b
1,
x b
4
(6.8)
Вероятность попадания в интервал:
1
1 d
d c
P( c X d ) f ( x )dx
dx
dx
b ac
b a
c
cb a
d
d
[ c,d ] [ a ,b ]
9.
Числовые характеристики равномерно распределенной случайной величины:mX
a b
(b a ) 2 b a
x
, DX
2 3
2
12
(6.9)
При необходимости определения параметров a и b по известным m(X),
D(X) используют следующие формулы:
a mx 3 x , b mx 3 x
(6.10)
Условия возникновения: Случайная величина Х - ошибки округления при
ограниченной разрядной сетке: ошибка при округлении счета до
ближайшего целого деленияОкругление до меньшего целогоX=[-1,0], m(X)=-0,5
Округление до большего целогоX=[0,1], m(X)=0,5
Округление до ближайшего целогоX=[-0,5;0,5],
m(X)=0, где 1 – вес
младшего разряда.
10. Экспоненциальное распределение
имеет непрерывная случайная величина T, принимающаятолько положительные значения, если ее плотность
вероятности и функция распределения равны:
1 e t , t 0,
F (t )
0, t 0.
t
e , t 0,
f (t )
0, t 0.
,
где – параметр распределения ( >0).
x
x
Т-положительная величина.
t 0 F ( t ) f ( t )dt 0 dt 0
t
0
t
t 0 F (t ) f ( x )dx 0 dx e dx e
0
x
(6.11)
x t
0
( e t e0 ) 1 e t
11.
Графикиплотности
и
распределения при =1.
функции
экспоненциального
f(x)
F(x)
1
1
0.5
0.5
2
4
0
2
4
Числовые характеристики экспоненциальной случайной
величины:
mT 1/ , DT 1/
2
(6.12)
Условия возникновения. Случайная величина T – интервал
времени между двумя соседними событиями в простейшем или
Пуассоновском потоке случайных событий, причем параметр
распределения – интенсивность потока.
12. Нормальное распределение (распределение Гаусса)
имеет непрерывная случайная величина Х, если ее плотностьвероятности и функция распределения равны:
( x m )2
x m
f (x )
exp
F ( x) 0.5
2
2 2
1
(6.13)
где m, σ - параметры распределения ( σ >0),
( x)
1
2
x
e
t2
2
dt
- функция Лапласа.
0
Числовые характеристики нормальной случайной величины:
mX m, DX
2
13.
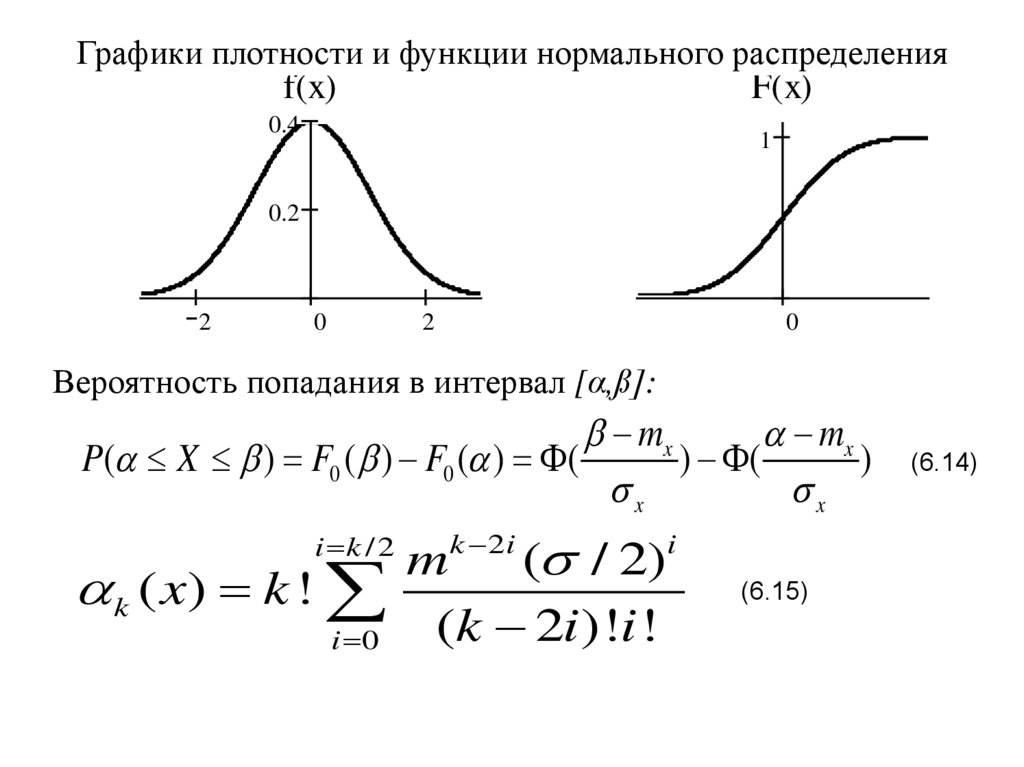
Графики плотности и функции нормального распределенияf(x)
F(x)
0.4
1
0.2
2
0
2
0
Вероятность попадания в интервал [α,ß]:
mx
mx
P( X ) F0 ( ) F0 ( ) (
) (
)
x
x
i k / 2
k ( x) k !
i 0
mk 2i ( / 2)i
(k 2i)!i !
(6.15)
(6.14)
14.
0, k нечетное,k ( x) k ! 2 k / 2
, k четное.
(k / 2)! 2
(6.16)
• Например, нормальный закон распределения имеют:
• - погрешности измерительных приборов; при этом
откалибрированный прибор не имеет
систематической погрешности, т.е. m=0, а величина
σ определяется классом точности измерительного
прибора;
• - параметры радиоэлектронных компонентов
(резисторов, конденсаторов, т.п.), причем m –
номинальное значение, указанное на маркировке, а
σ определяется классом точности.












 mathematics
mathematics








