Непрерывные случайные величины

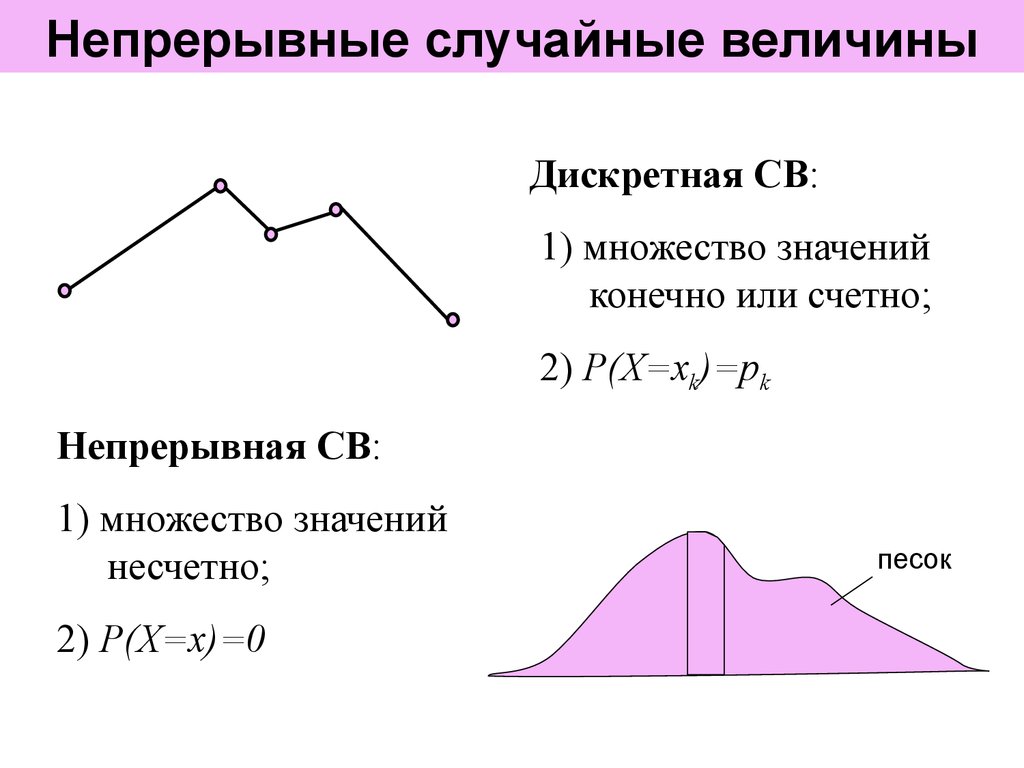
1. Непрерывные случайные величины

Дискретная СВ:
1) множество значений
конечно или счетно;
2) Р(Х=хk)=pk
Непрерывная СВ:
1) множество значений
несчетно;
2) P(X=x)=0
песок

2. Функция распределения НСВ

F x
F x P X x
1
х
0
Свойства функции распределения
1. 0 F x 1 x ;
2. x1 x2 F x1 F x2
3. F x
F x0
x x0
4. F 0,
F 1
5. Ð c X d
F d F c

3. Плотность распределения НСВ

f (x)
х
f ( x ) F x
x
P( x X x x ) F x x F ( x )
P x x P x
f ( x ) lim
x
x 0
P( x X x x) f ( x) x o( x)

4. Плотность распределения НСВ

P ( x X x x) f ( x) x o( x)
Свойства плотности распределения
x
1. f ( x ) 0
2.
f ( x)dx 1
3. F ( x)
f (t )dt
4. f ( x) F ( x)
5. P (c X d )
d
f ( x)dx
c

5. Преобразование случайной величины

Теорема 1. Пусть f X x - плотность распределения
с.в. Х, а с.в. Y=a+bX. Тогда
1
y a
f Y x f X
b
b
y a
F X b , если b 0
FY y
1 F y a , если b 0
X
b

6. Преобразование случайной величины

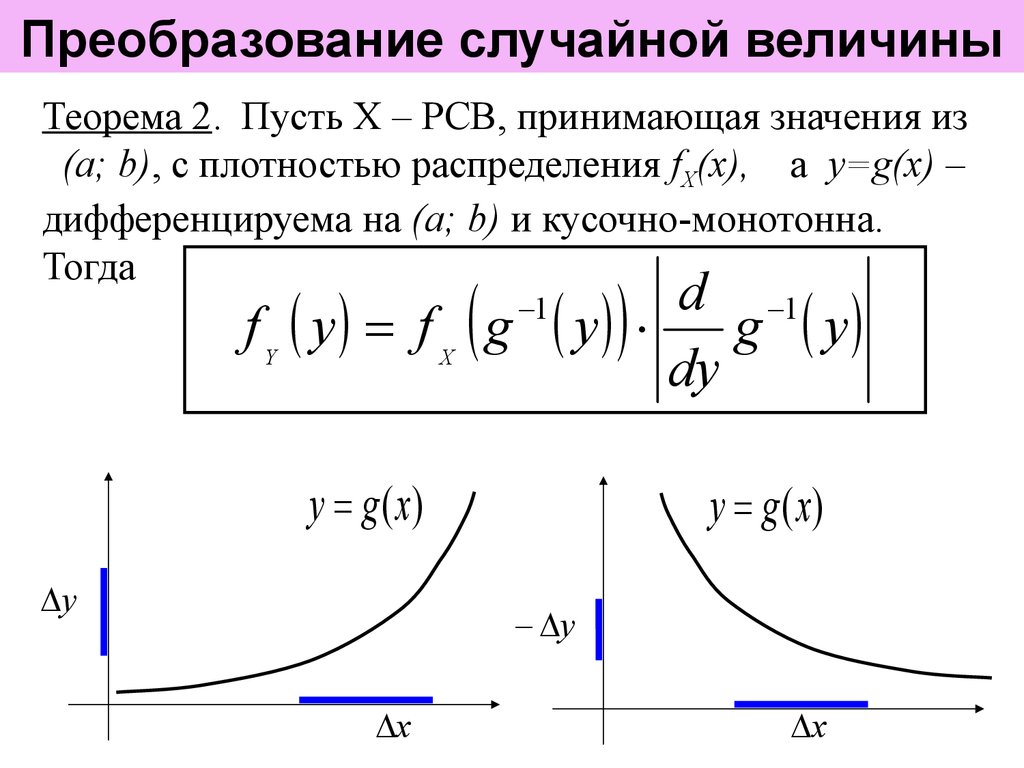
Теорема 2. Пусть Х – РСВ, принимающая значения из
(a; b), с плотностью распределения fХ(x), а y=g(x) –
дифференцируема на (a; b) и кусочно-монотонна.
Тогда
d 1
f Y y f X g y
g y
dy
1
y g (x)
y
y g (x)
y
x
x

7. Числовые характеристики

Название
Математич
еское
ожидание
Начальны
й момент
Центральн
ый момент
Дисперсия
ДСВ
Определение
mX M X
mr
s
M X
M X s
xi pi
i
r
x
i pi
r
D M X2
i
s
(
x
m
)
pi
i
i
2
(
x
m
)
pi
i
i
При условии
Ряды
абсолютно
сходятся
НСВ
x
f ( x ) dx
r
x
f ( x)dx
s
(
x
m
)
f ( x)dx
2
(
x
m
)
f ( x)dx
Интегралы
абсолютно
сходятся

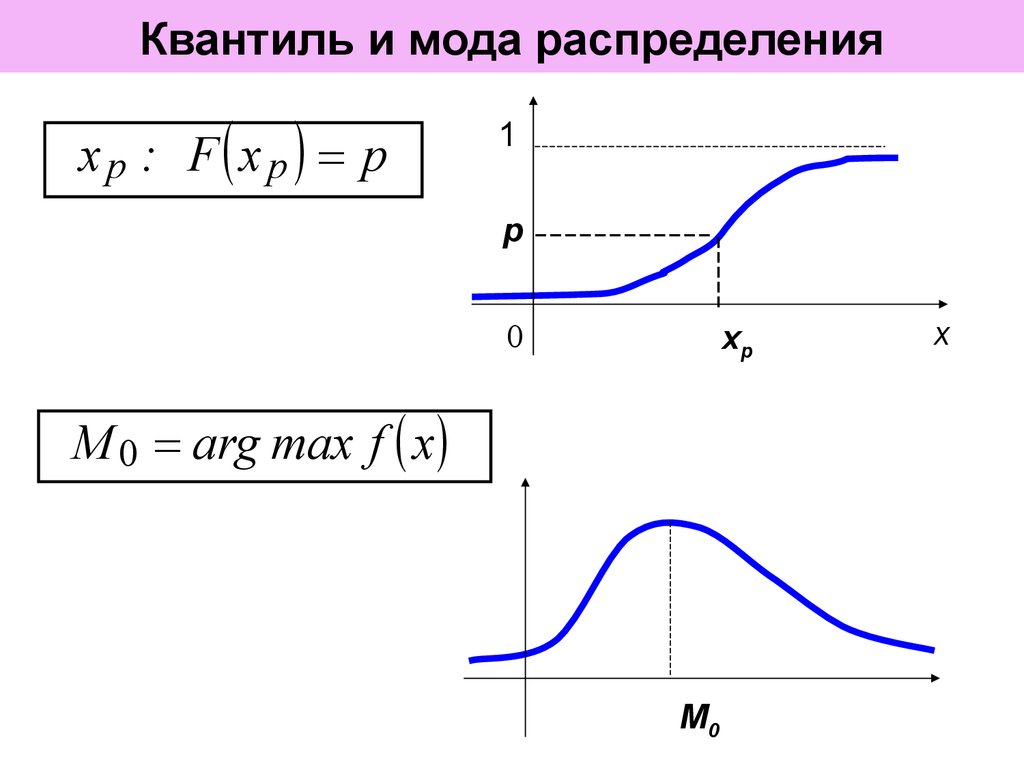
8. Квантиль и мода распределения

xp : F xp p
1
р
0
хр
М 0 arg max f x
М0
х

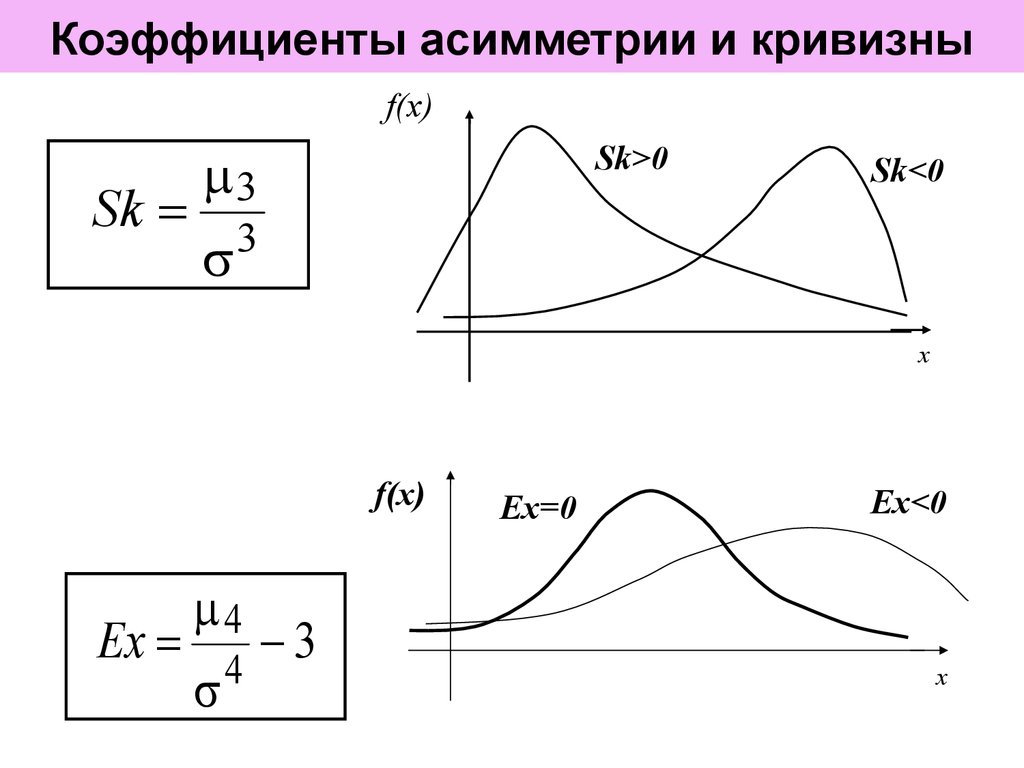
9. Коэффициенты асимметрии и кривизны

f(x)
Sk
Sk>0
3
Sk<0
3
x
f(x)
Εx
4
4
3
Ex=0
Ex<0
x