Similar presentations:
Числовые характеристики случайных величин. Математическое ожидание
1.
2.
Срез знаний1 вариант
1)
2)
3)
3 вариант
Следует ли для непрерывных случайных
величин, что если Р(Х=С)=0, то это событие
невозможно? Почему?
Приведите пример дискретной случайной
величины.
Случайная величина Х задана функцией
распределения: 0,
при
x 1,
1) Что называется плотностью вероятности
случайной величины?
2) Что
называют законом распределения
дискретной случайной величины?
F ( X ) a ( x 1) 2 , при 1 x 2,
1,
при
x 2.
Найти значение a, построить графики F(x) и f(x).
2 вариант
1) Что представляет собой величина
F ( x x) F ( x)
x
2)
3)
Что
называется
многоугольником
распределения?
Кривая распределения н.с.в. Х имеет вид,
указанный на рисунке.
4 вариант
1)
Как определяется произведение случайных
величин?
Какая случайная величина называется
дискретной?
3) Кривая распределения н.с.в. Х имеет вид,
указанный на рисунке.
2)
3.
Лекция 4. Числовые характеристики случайных величинЧисловые характеристики случайных величин – числовые параметры,
характеризующие отдельные существенные свойства (черты) закона
распределения случайных величин.
Рассматриваются две основные группы числовых характеристик
случайных величин:
1) Характеристики положения:
– математическое ожидание (M[X], mx):
– мода (Мо);
– медиана (Me);
2) Характеристики рассеивания (разброса):
– дисперсия (D[X], Dx);
– среднее квадратическое отклонение .
4.
Математическим ожиданием д.с.в. Х, имеющей законраспределения
x1
p1
x2
…
xn
p2
…
pn
называется число, равное сумме произведений всех ее значений
на соответствующие им вероятности.
Математическое ожидание случайной величины x обозначается
MХ, М(Х), ЕХ, mХ, aХ или М[Х].
Расчетная формула:
n
M [ X ] xi pi
i 1
где X – дискретная случайная величина.
5.
Среднее арифметическое значений,принимаемых случайной величиной в
длинной серии опытов, приближенно
равно ее математическому ожиданию.
6.
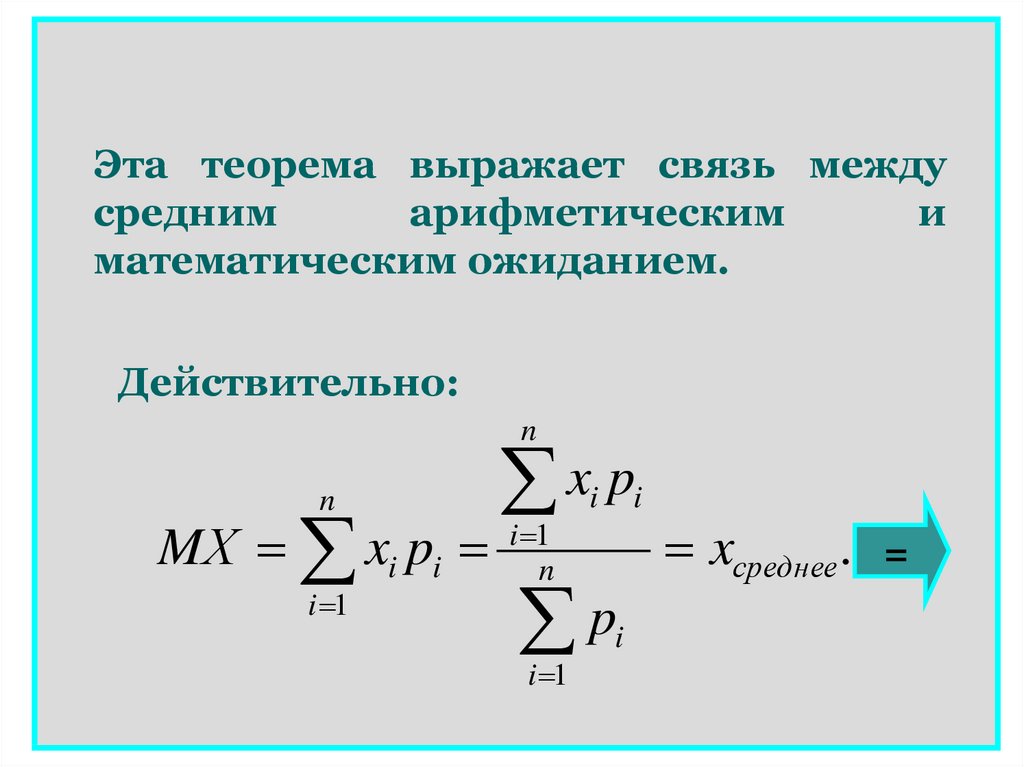
Эта теорема выражает связь междусредним
арифметическим
и
математическим ожиданием.
Действительно:
n
n
MХ xi pi
i 1
x p
i 1
n
i
i
p
i 1
i
xсреднее.
=
7.
Математическим ожиданием н.с.в. Х с плотностьювероятности f(x), называется число
M [ X ] x f ( x)dx.
Интеграл предполагается абсолютно сходящимся.
Смысл математического ожидания остается таким же, как и
в случае дискретных случайных величин. Меняется вид
формулы путем замены:
xi x
pi f ( x)dx
8.
СВОЙСТВАМАТЕМАТИЧЕСКОГО
ОЖИДАНИЯ
1
Математическое ожидание от
постоянной величины равно
этой постоянной величине:
М[C]=C, C=const
9.
Рассмотримряд
распределения
случайной величины Х=С:
С
1
Тогда математическое ожидание будет
равно
М[C]=C
10.
2Постоянную величину можно
выносить за знак математического
ожидания:
М[с X]=с M[X], где с=cоnst.
11.
Используем определение мат. ожидания:M [сX ] с хi pi
=
i
Постоянную с можно вынести за знак
суммы:
=
с xi pi с M [ X ]
i
12.
3Математическое ожидание суммы
случайных величин Х и У равно
сумме математических ожиданий
этих величин:
М[X+Y]=M[X]+M[Y]
13.
Распишем математическое ожиданиесуммы двух случайных величин по
определению:
n
m
n
m
M [ X Y ] ( xi y j ) pij xi pij
i 1 j 1
i 1 j 1
n
m
n
m
n
m
i 1
j 1
j 1
i 1
y j pij xi pij y j pij
i 1 j 1
n
m
i 1
j 1
xi pi y j p j MX MY .
14.
4Математическое ожидание отклонения
случайной величины Х от ее
математического ожидания равно
нулю, т.е.:
М[X-MX]=0.
15.
Согласно свойствам 1 и 3, имеем:M [ X MX ] MX M [ MX ] MX MX 0.
Разность Х-МХ называется отклонением
с.в. Х от ее математического ожидания и
обозначается:
X X MX .
X -
центрированная
величина.
случайная
16.
5Математическое ожидание
произведения
независимых случайных величин
Х и У равно произведению
математических ожиданий этих
величин:
М[XY]=M[X]M[Y]
17.
Распишем математическое ожиданиепо определению:
M [ XY ] с p( XY c) a b p( X a, Y b) =
с
a ,b
Для независимых случайных величин:
p( X a, Y b) p( X a) p(Y b)
Тогда:
=
a p( X a) b p( X b) M [ X ] M [Y ]
a
b
18.
Свойства математического ожидания, доказанные для д.с.в.,остаются справедливыми и для непрерывных с.в.
Например,
Mсс сx f ( x)dx с x f ( x)dx сMX .
19.
20.
Функция распределения непрерывнойслучайной величины задана выражением:
0, x 0
2
F ( x) ax , 0 x 1
1, x 1
Найти величину a, плотность вероятности,
вероятность попадания на участок (0.25-0.5) и
математическое ожидание.
21.
1.Так как функция распределения F(x)
непрерывна,
то
при
х=1
ax2=1,
следовательно, a=1.
2. Плотность вероятности находится, как
производная от функции распределения:
0, x 0
f ( x) F ( x) 2 x, 0 x 1
0, x 1
22.
3. Вычисление вероятности попадания на заданныйучасток может быть произведено двумя
способами: с помощью функции распределения и
с помощью плотности вероятности.
1 способ.
Используем формулу нахождения вероятности
через функцию распределения:
p (0.25 x 0.5) F (0.5) F (0.25)
0.5 0.25 0.1875
2
2
23.
2 способ.Используем формулу нахождения вероятности
через плотность вероятности:
0.5
p(0.25 X 0.5)
2 xdx x
2 0.5
0.25
0.1875
0.25
4. Находим математическое ожидание:
M [ X ] x f ( x)dx
1
2x
M [ X ] x 2 xdx
3
0
3 1
0
2
3
24.
Случайная величина Х подчиняетсязакону распределения
ax, 0 x 1
f ( x)
0, x 0, x 1
Найти величину a и функцию распределения.
25.
1. Для нахождения параметра a используемсвойство плотности распределения:
f ( x ) dx 1
1
ax
0 a x dx 2
2 1
0
a
1
2
a 2
2.
Функция распределения находится
интегрирования плотности вероятности:
путем
26.
xF ( x)
x
f ( x)dx
2
2
xdx
x
0
При 0<x<1. Тогда:
0, x 0
2
F ( x) x , 0 x 1
1, x 1
27.
1. Что называется математическим ожиданием дискретной случайной величины?2. Свойства математического ожидания.
3. Доказать, что математическое ожидание числа появлений события А в одном
испытании равно вероятности появления р события А.
4. Доказать, что математическое ожидание дискретной случайной величины Х –
числа появлений события А в n независимых испытаниях, в каждом из которых
вероятность появления события равна р – равно произведению числа
испытаний на вероятность появления события в одном испытании, т. е. доказать,
что M ( X ) = np.
5. Доказать, что M (Y ) = aM ( X ) + b, если Y = aX + b.
6. Доказать, что M ( X − M ( X )) = 0.
7. Доказать, что M (M ( X )) = M ( X ).
8. Доказать, что математическое ожидание дискретной случайной величины
заключено между наименьшим и наибольшим её возможными значениями.
9. Доказать, что если случайные величины X1 , X 2 ,..., X n независимы,
положительны и одинаково распределены, то
10. Случайная величина задана плотностью распределения. Найти математическое
ожидание случайной величины.


























 mathematics
mathematics








