Числовые характеристики случайных величин

1. Урок 15

Числовые характеристики
случайных величин
Презентацию подготовил
студент группы ПОВ 54/2
Фомин Евгений
2011 год

2. Числовые характеристики случайных величин

Назначение числовых характеристик случайной величины – в
сжатой форме выразить наиболее важные черты распределения.
Математическое ожидание
Свойства математического ожидания
Дисперсия
Свойства дисперсии
Тесты

3. Математическое ожидание

X
x1
x2
…
xi
…
xn
P(X)
p1
p2
…
pi
…
pn
Математическим ожиданием М(X) дискретной случайной величины Х
называется сумма произведений всех возможных значений
случайной величины на соответствующие вероятности значений:
n
M (X) = x1p1 + ….+ xnpn = xi pi
i 1
Пример:
X
2
5
8
19
P
0,2
0,3
0,4
0,1
M (X) = 2 0,2 + 5 0,3 + 8 0,4 + 19 0,1 = 7.

4.

Свойства математического ожидания
1. Математическое ожидание постоянной величины равно самой постоянной
M (const) = const.
2. Постоянный множитель случайной величины может быть вынесен за знак
математического ожидания
M (const X) = const M (X).
3. Математическое ожидание алгебраической суммы двух случайных величин Х и У
равно алгебраической сумме их математических ожиданий
M (X × Y) = M (X) + M (Y).
4. Математическое ожидание произведения двух независимых случайных величин
X и Y равно произведению их математических ожиданий
M (X × Y) = M (X) × M (Y).
5. Математическое ожидание отклонения X–M[X] случайной величины X от ее
математического ожидания M[X] равно нулю
M (X – M (X)) = 0.

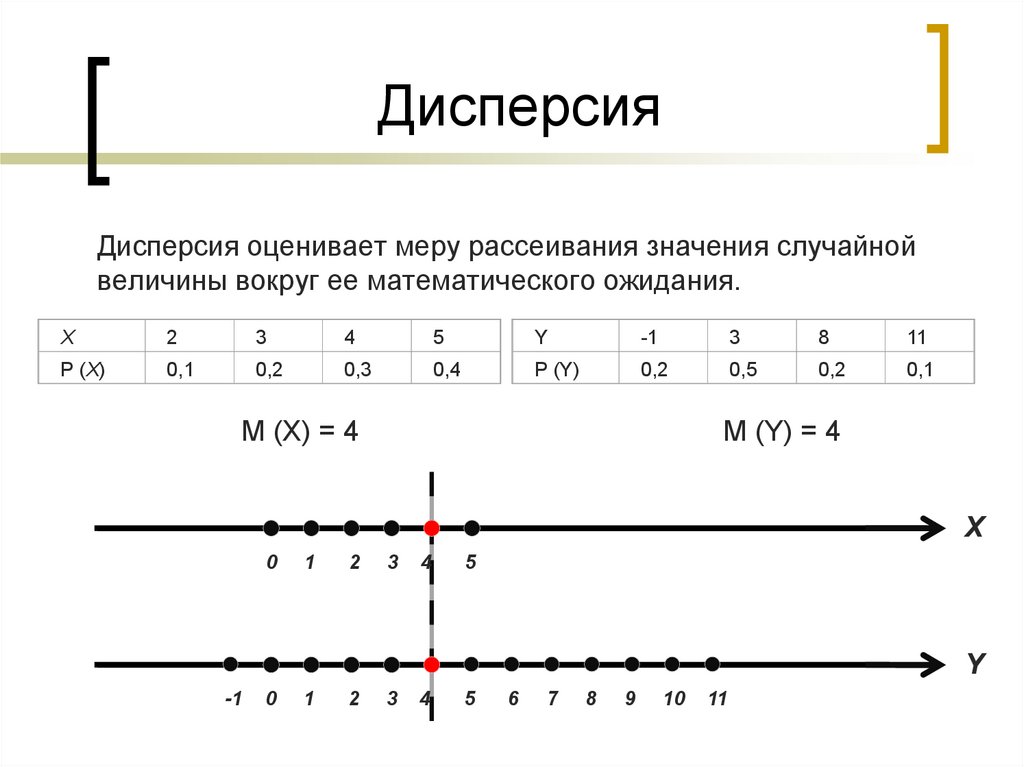
5. Дисперсия

Дисперсия оценивает меру рассеивания значения случайной
величины вокруг ее математического ожидания.
X
2
3
4
5
Y
-1
3
8
11
P (X)
0,1
0,2
0,3
0,4
P (Y)
0,2
0,5
0,2
0,1
M (X) = 4
M (Y) = 4
X
0
1
2
3
4
5
Y
-1
0
1
2
3
4
5
6
7
8
9
10
11

6. Дисперсия

Дисперсией случайной величины Х называют Математическое
ожидание квадрата отклонения случайной величины Х от ее
математического ожидания M (X).
Для дискретной случайной величины:
n
2
D ( X ) ( X i M ( X )) Pi
i 1
Для непрерывной случайной величины :
2
D ( X ) ( X M ( X )) f ( X ) dx
Среднее квадратическое отклонение:
( X ) D( X )

7. Свойства дисперсии

1.
Дисперсия постоянной величины равна нулю
D (const) = 0.
2.
Постоянный множитель случайной величины можно выносить за знак дисперсии,
предварительно возведя его в квадрат
D (const X) = const2 D (X).
3.
Дисперсия алгебраической суммы двух независимых случайных величин Х и Y равна
сумме дисперсий этих величин
D (X Y) = D(X) + D(Y).
4.
Дисперсия случайной величины Х равна разности между математическим
ожиданием квадрата случайной величины и квадратом ее математического
ожидания.
D (X) = M (X2) – (M (X))2

8. Единицы измерения

Среднеквадратичное отклонение
измеряется в той же единице
измерения что и случайная величина.
Дисперсия измеряется в той же
единице измерения что и случайная
величина, но в квадрате.

9. Пример

Для случайной величины X задан ряд
распределения:
xi
0
2
4
pi
0.3
0.3
0.4

10. Пример

Найдем математическое ожидание
M(X) = 0 ∙ 0.3 + 2 ∙ 0.3 + 4 ∙ 0.4 = 2.2
M(X2) = 02 ∙ 0.3 + 22 ∙ 0.3 + 42 ∙ 0.4 = 7.6
дисперсию:
D(X) = M(x2) - (M(x))2 = 7.6 - 4.84 = 2.76.

11. Пример

Отсюда можем найти
среднеквадратичное отклонение:
σ = √D(X) = √2.76 ≈ 1.66;
Теперь отметим всё это на графике…

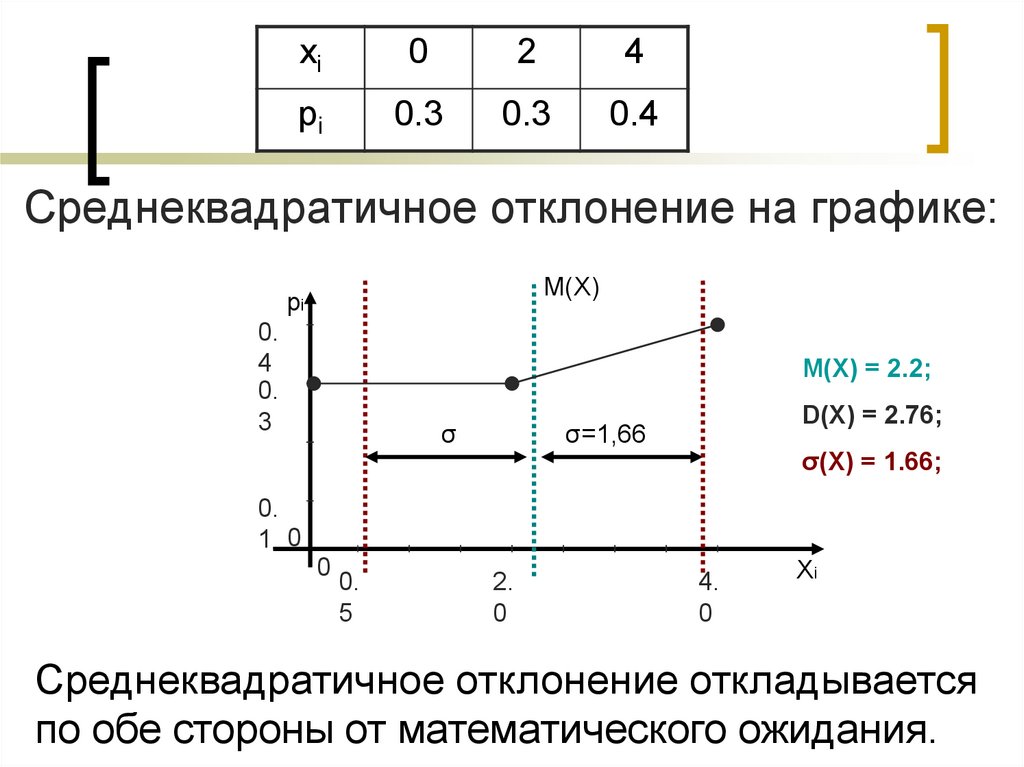
12.

xi
0
2
4
pi
0.3
0.3
0.4
Среднеквадратичное отклонение на графике:
M(X)
pi
0.
4
0.
3
M(X) = 2.2;
D(X) = 2.76;
σ=1,66
σ
σ(X) = 1.66;
0.
1 0
0
0.
5
2.
0
4.
0
Xi
Среднеквадратичное отклонение откладывается
по обе стороны от математического ожидания.

13.

14. Тесты

15. 1. Чему равно математическое ожидание постоянной величины (M (const))?

1.
M (const) = 0
2.
M (const) = M (X)
3.
M (const) = const
4.
M (const) = M (Y)

16. 2. Чему равно математическое ожидание отклонения X – M [X] случайной величины X от ее математического ожидания M [X]

1.
M (X – M (X)) = М (Х)
2.
M (X – M (X)) = - X
3.
M (X – M (X)) = 1
4.
M (X – M (X)) = 0

17. 3. Чему равно среднее квадратическое отклонение?

1.
2.
3.
4.
(X ) M (X )
(X )
D( X )
( X ) D( X )
(X ) 0

18. 4. Чему равна дисперсия постоянной величины (D (const))?

1.
D (const) = const
2.
D (const) = 0
3.
D (const) = M (X)
4.
D (const) = 1

19. 5. Вам понравилась моя презентация?

1.
Да
2.
Презентация?!
3.
Нет
4.
Я не смотрел

20. Спасибо за внимание!