Числовые характеристики случайных величин. Лекция 6

1.

ФГБОУ ВО «УлГПУ им. И.Н. Ульянова»
Теория вероятностей и математическая статистика
лектор Макеева О.В.
Лекция 6
Числовые
характеристики
случайных величин
1. Математическое ожидание
2. Дисперсия и среднее квадратичное отклонение
3. Мода и медиана
4. Начальные и центральные моменты
5. Асимметрия и эксцесс
6. Числовые характеристики распределений

2.

Пролог
Закон
распределения
дискретной
случайной
величины или функция, задающая непрерывную
случайную
величину
(функция
распределения,
плотность вероятности) дают полную информацию о
случайной величине. Однако на практике иногда
бывает удобнее использовать краткую (неполную)
характеристику случайной величины с помощью числа.
К таким числовым характеристикам случайных
величин относятся: математическое ожидание,
дисперсия, среднее квадратичное отклонение, мода,
медиана (для непрерывных величин), начальные и
центральные моменты, асимметрия и эксцесс.
Лекция 6. Характеристики случайных величин 2

3.

§1. Математическое ожидание
Математическое
ожидание
(среднее
значение)
случайной
величины
является
характеристикой её положения и определяет центр
распределения.
Математическое ожидание M(X) дискретной
случайной величины X равно сумме произведений
возможных значений величины xi на соответствующие
им вероятности pi:
n
M X xi pi .
i 1
(1)
Лекция 6. Характеристики случайных величин 3

4.

§1. Математическое ожидание
Математическое ожидание M(X) дискретной
случайной величины X с бесконечным счётным числом
значений равно сумме ряда:
M X xi pi .
i 1
(1 )
Математическое ожидание M(X) непрерывной
случайной величины равно несобственному интегралу
от произведения непрерывно изменяющегося значения
величины x на элемент вероятности (x)dx, где (x) –
плотность вероятности случайной величины X:
M X x x dx.
(2)
Лекция 6. Характеристики случайных величин 4

5.

§1. Математическое ожидание
Свойства математического ожидания.
1. Математическое ожидание константы (постоянной
величины) равно самой величине:
M С С.
(3)
2. Постоянный множитель можно выносить за знак
математического ожидания:
M k X k M X .
Утверждение
следует
математического ожидания:
из
n
n
i 1
i 1
(4)
определения
M k X k xi pi k xi pi k M X .
Лекция 6. Характеристики случайных величин 5

6.

§1. Математическое ожидание
Свойства математического ожидания.
3. Математическое ожидание алгебраической суммы
конечного числа случайных величин равно такой же
сумме их математических ожиданий:
M X Y M X M Y .
Утверждение
следует
математического ожидания:
из
(5)
определения
M X Y xi y j pij xi pij y j pij
n
m
i 1 j 1
n
m
i 1 j 1
n
m
i 1 j 1
x p y p M X M Y ; p P X x Y y .
n
i 1
m
i
i
j 1
j
j
ij
i
j
Лекция 6. Характеристики случайных величин 6

7.

§1. Математическое ожидание
Свойства математического ожидания.
4. Математическое ожидание произведения конечного
числа независимых случайных величин равно
произведению их математических ожиданий:
M X Y M X M Y .
Утверждение
следует
математического ожидания:
из
(6)
определения
M X Y xi y j pij xi y j pi p j
n
m
n
i 1 j 1
n
m
i 1 j 1
m
x p y p M X M Y ;
p P X x Y y P X x P Y y p p .
i 1
ij
i
i
i
j 1
j
j
j
i
j
i
j
Лекция 6. Характеристики случайных величин 7

8.

§1. Математическое ожидание
Свойства математического ожидания.
5. Математическое ожидание отклонения случайной
величины от её математического ожидания равно
нулю:
M X M X 0.
Утверждение следует из
математического ожидания:
свойств
(7)
(1)
и
(3)
M X M X M X M M X
M X M X 0.
Лекция 6. Характеристики случайных величин 8

9.

§2. Дисперсия
Определение 1. Дисперсия случайной величины
это математическое ожидание квадрата отклонения
случайной величины от её математического ожидания:
D X M X M X .
(8)
D X xi a pi ,
(9)
2
Дисперсия (лат. dispersio – рассеяние) случайной
величины является характеристикой распределения её
вероятностей.
Формулы для вычисления дисперсии дискретной и
непрерывной случайны величины X с математическим
ожиданием а имеют вид: n
2
i 1
D X x a x dx.
2
(10)
Лекция 6. Характеристики случайных величин 9

10.

§2. Дисперсия
Свойства дисперсии.
1. Дисперсия константы равна нулю:
D C 0.
(11)
Утверждение следует из определения дисперсии:
D С M C M C M C C M 0 0.
2
2
2. Постоянный множитель можно выносить за знак
дисперсии, возводя его в квадрат:
D k X k D X .
2
Утверждение
следует
математического ожидания:
из
(12)
свойства
(2)
D k X M kX M kX M kX kM X
2
2
2
2
M k X M X k M X M X k 2 D X .
Лекция 6. Характеристики случайных величин 10
2
2

11.

§2. Дисперсия
Свойства дисперсии.
3. Дисперсия случайной величины равна разности
математического ожидания квадрата этой величины
и квадрата её математического ожидания:
D X M X M X . (13)
2
2
Утверждение следует из определения дисперсии:
D X M X M X M X 2 X M X M X
2
2
M X M 2 X M X M M X
2
2
M X 2M X M X M X
2
2
2
M X M X .
2
2
Лекция 6. Характеристики случайных величин 11

12.

§2. Дисперсия
Свойства дисперсии.
4. Дисперсия алгебраической суммы конечного числа
независимых случайных величин равна сумме их
дисперсий:
D X Y D X D Y .
(14)
Утверждение следует из свойства (3) дисперсии:
D X Y M X Y M X Y
2
2
M X 2 XY Y M X M Y
M X 2 2M XY M Y 2
2
2
2
M X 2M X M Y M Y
2
2
2
2
M X M X M Y M Y D X D Y .
2
2
Лекция 6. Характеристики случайных величин 12

13.

§2. Дисперсия
Дисперсия случайной величины имеет размерность
квадрата этой величины, что не всегда удобно. Поэтому
в качестве показателя рассеяния используют также
величину D X .
Определение 2.
Среднее квадратичное отклонение случайной
величины – это арифметическое значение квадратного
корня из её дисперсии:
X D X .
(15)
Лекция 6. Характеристики случайных величин 13

14.

Пример 1
Эксперимент: выбрать наугад деталь для проверки
качества.
N=10 – число всех деталей в партии (объектов);
M=4 – число бракованных деталей в партии (объектов,
обладающих заданным свойством);
n=3 – число деталей, отобранных для проверки
качества.
Величина Х: число бракованных деталей среди
отобранных для проверки качества.
CMm CNn mM
P X m
CNn
xi
0
1
2
3
pi
20/120
60/120
36/120
4/120
Лекция 6. Характеристики случайных величин 14

15.

Пример 1
Величина Х: число бракованных
отобранных для проверки качества.
i
1
2
3
4
xi
0
1
2
3
pi
20/120
60/120
36/120
4/120
деталей
среди
4
M X xi pi
i 1
20
60
36
4
0
1
2
3
120
120
120
120
0 60 72 12 144 12 6
1, 2 1.
120
120 10 5
Лекция 6. Характеристики случайных величин 15

16.

Пример 1
Величина Х: число бракованных
отобранных для проверки качества.
i
1
2
3
4
xi
0
1
2
3
pi
20/120
60/120
36/120
4/120
4
D X x pi M X
i 1
2
i
деталей
среди
2
20 2 60
4
2 36
2
0
1
2
3
1, 22
120
120
120
120
0 60 144 36
240
1, 44
1, 44 2 1, 44 0,56.
120
120
2
Лекция 6. Характеристики случайных величин 16

17.

Пример 1
Величина Х: число бракованных
отобранных для проверки качества.
i
1
2
3
4
xi
0
1
2
3
pi
20/120
60/120
36/120
4/120
деталей
среди
X D X 0,56 0,7.
Лекция 6. Характеристики случайных величин 17

18.

Пример 2
Эксперимент:
выбрать наугад
время
прихода
пассажира на остановку в диапазоне [0; 2].
(Диапазон
определяется
графиком
регулярного
(равномерного) движения транспорта).
Событие A: время ожидания пассажиром автобуса
составит не больше полминуты.
Величина Х: время ожидания пассажиром автобуса.
1
при 0 x 2,
x 2
0 при x 0, x 2.
Лекция 6. Характеристики случайных величин 18

19.

Пример 2
Величина Х: время ожидания пассажиром автобуса.
1
при 0 x 2,
x 2
0 при x 0, x 2.
M X x x dx
2
2
2 2
1
1
1 x
1 2 2
1
x dx xdx
2 0 4 1.
2
2 0
2 2 0 4
4
0
Лекция 6. Характеристики случайных величин 19

20.

Пример 2
Величина Х: время ожидания пассажиром автобуса.
1
при 0 x 2,
x 2
0 при x 0, x 2.
D X x x dx M X
2
2
2
2
3 2
1
1
1 x
1 3 3
2
2
x dx 1 x dx 1
1 2 0 1
2
2 0
2 3 0
6
0
2
1
4
1
8 1 1 .
6
3
3
Лекция 6. Характеристики случайных величин 20

21.

Пример 2
Величина Х: время ожидания пассажиром автобуса.
1
при 0 x 2,
x 2
0 при x 0, x 2.
1
3
X D X
0, 6.
3
3
Лекция 6. Характеристики случайных величин 21

22.

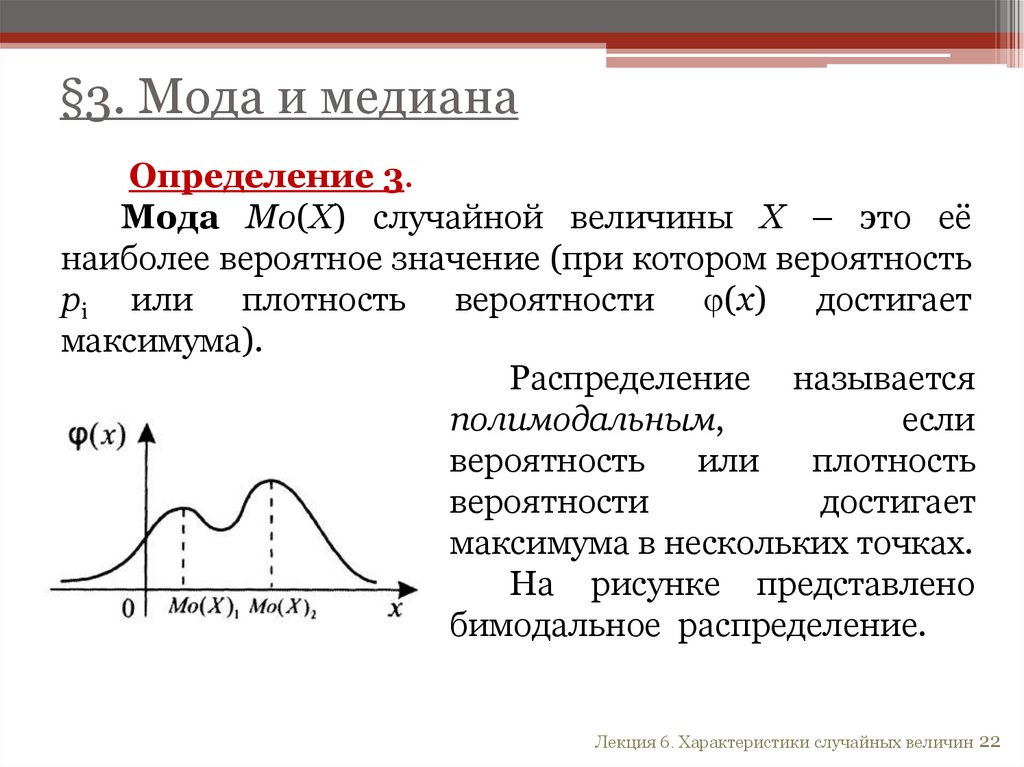
§3. Мода и медиана
Определение 3.
Мода Mo(X) случайной величины Х – это её
наиболее вероятное значение (при котором вероятность
pi или плотность вероятности (х) достигает
максимума).
Распределение называется
полимодальным,
если
вероятность
или
плотность
вероятности
достигает
максимума в нескольких точках.
На рисунке представлено
бимодальное распределение.
Лекция 6. Характеристики случайных величин 22

23.

§3. Мода и медиана
Определение 4.
Медиана Mе(X) непрерывной случайной величины
Х – это её значение для которого вероятность того, что
величина Х примет значение меньше или больше
Mе(X), равна 1/2:
1
P X Me X P X Me X .
2
Прямая
х=Ме(Х)
делит
фигуру
под
кривой распределения
на две равновеликие
части площадью ½.
Лекция 6. Характеристики случайных величин 23

24.

§4. Моменты
Определение 5.
Начальный момент k-го порядка k(X)
случайной величины Х – это математическое ожидание
k-ой степени величины X:
k X M X K .
(16)
Определение 6.
Центральный момент k-го порядка k(X)
случайной величины Х – это математическое ожидание
k-ой степени отклонения величины X от её
математического ожидания:
k X M X M X
K
. (17)
Лекция 6. Характеристики случайных величин 24

25.

§4. Моменты
Для случайной величины Х с математическим
ожиданием а формулы для вычисления моментов
имеют следующий вид:
Очевидно, что 1(X)=M(X) – начальный момент
первого порядка равен математическому ожиданию, а
2(X)=D(X) – центральный момент второго порядка
равен дисперсии.
Лекция 6. Характеристики случайных величин 25

26.

§5. Асимметрия и эксцесс
Определение 7.
Коэффициент асимметрии A(X) случайной
величины Х – это отношение центрального момента
третьего порядка величины к кубу её среднего
квадратичного отклонения:
3 X
A X 3
.
X
(18)
Распределение,
симметричное
относительно
математического ожидания имеет нулевую асимметрию
A X 0
Правостороннее распределение
– с положительной асимметрией –
имеет более длинный правый
«хвост» распределения.
Лекция 6. Характеристики случайных величин 26

27.

§5. Асимметрия и эксцесс
Определение 8.
Коэффициент
эксцесса
E(X)
случайной
величины Х – это отношение центрального момента
четвёртого порядка величины к четвёртой степени её
среднего квадратичного отклонения уменьшенное на 3:
4 X
E X 4
3.
X
(19)
Стандартное нормальное распределение (с нулевым
математическим ожиданием и единичной дисперсией)
имеет нулевой эксцесс.
Островершинное распределение
имеет
положительный
эксцесс,
плосковершинное – отрицательный.
Лекция 6. Характеристики случайных величин 27

28.

§6. Характеристики распределений
Теорема 1.
Математическое
ожидание
случайной
величины
Х,
имеющей
биномиальное
распределение с параметрами n и p, равно
M(X)=np, а дисперсия равна D(X)=npq.
Доказательство.
Пусть случайная величина X число наступлений
события А в n независимых испытаниях, тогда
Х=Х1+Х2+…+Хn, где Хk – число наступлений события А в
испытании с номером k (k=1, 2, …, n).
Лекция 6. Характеристики случайных величин 28

29.

§6. Характеристики распределений
n
n
M X M Xk M Xk
k 1
k 1
n
n
k 1
k 1
0 q 1 p p np.
n
n
D X D Xk D Xk
k 1 k 1
n
n
0 p q 1 p p p 2 q q 2 p
k 1
k 1
2
2
n
n
k 1
k 1
pq p q pq npq.
Лекция 6. Характеристики случайных величин 29

30.

§6. Характеристики распределений
Теорема 2.
Математическое ожидание и дисперсия
случайной
величины
Х,
имеющей
распределение Пуассона, равны параметру
этого распределения , т.е. M(X)=D(X)= .
Доказательство.
m
i 1
m 1
m!
M X xi pi m
2
e 1
1! 2!
n
n!
e e
m 1
m 1
m 1 !
e
e .
Лекция 6. Характеристики случайных величин 30

31.

§6. Характеристики распределений
m
m
1
1
2
2
M X m
e e
m!
m 1 !
m 1
m 1
2e
m 2
m
m 2
m 2 !
e
m 1
m 1
m 1 !
2
n
2
e 1
n!
1! 2!
2
n
e 1
2 e e e e 2 ;
n!
1! 2!
D X M X M X 2 2 .
2
2
Лекция 6. Характеристики случайных величин 31

32.

§6. Характеристики распределений
Теорема 3.
Математическое
ожидание
случайной
величины
Х,
имеющей
геометрическое
распределение с параметром p, равно M(X)=1/p,
а дисперсия равна D(X)=q/p2.
Доказательство.
i 1
n 1
n 1
M X xi pi n pq n 1 p n q n 1
p 1 2q 3q nq p q q q
q
1
1
p 1
p
1 p
2 .
p
2
1 q p p
1 q
1 q
2
n 1
2
3
q
n
Лекция 6. Характеристики случайных величин 32

33.

§6. Характеристики распределений
M X 2 n 2 pq n 1 p 1 22 q 32 q 2
n 1
p q 2q 2 3q 3
p q 1 2q 3q
2
nq
nq n
n 1
n 2 q n 1
2
q
1 q q 2 1 q
1 q
1 q
p
p
2 ;
p
2
4
3
1 q
p
1 q
1 q
2
1 q 1
q
2
D X M X M X 2 2 2 .
p
p
p
Лекция 6. Характеристики случайных величин 33

34.

§6. Характеристики распределений
Теорема 4.
Математическое
ожидание
случайной
величины Х, имеющей гипергеометрическое
распределение с параметром n, M, N равно
M
M X n ,
N
а дисперсия равна
M M
n
D X n
1 1 .
N 1
N N
Лекция 6. Характеристики случайных величин 34

35.

Пример 1
Величина Х: число бракованных деталей
отобранных для проверки качества (стр. 14-17).
i
1
2
3
4
xi
0
1
2
3
pi
20/120
60/120
36/120
4/120
среди
M
4 12
M X n
3 1, 2;
N
10 10
M M
n
D X n
1 1
N 1
N N
4
4
3 4 6 7 4 2 7
3 1 1
0,56.
9 10 10 3 10 10
100
Лекция 6. Характеристики случайных величин 35

36.

§6. Характеристики распределений
Теорема 5.
Математическое
ожидание
случайной
величины
Х,
имеющей
равномерное
распределение на отрезке [а, b] равно
M(X)=(a+b)/2, а дисперсия равна D(X)=(b-a)2/12.
Доказательство.
b
1
M X x x dx x
dx
b a
a
2 b
1 x
b2 a 2
b a
;
b a 2 a 2 b a
2
Лекция 6. Характеристики случайных величин 36

37.

§6. Характеристики распределений
a b dx
D X x M X x dx x
2 b a
a
2
b
2
3
3
b a a b
1
a b
1
x
3 b a
2
3 b a 8
8
a
3
3
2
b a b a
b a
1
.
3 b a 8
8
12
3 b
Лекция 6. Характеристики случайных величин 37

38.

Пример 2
Величина Х: время ожидания пассажиром автобуса
(стр. 18-21).
1
при 0 x 2,
x 2
0 при x 0, x 2.
a b 0 2
M X
1;
2
2
b a
2 0
4
D X
.
2
12
2
12
3
Лекция 6. Характеристики случайных величин 38

39.

§6. Характеристики распределений
Теорема 6.
Математическое
ожидание
случайной
величины
Х,
имеющей
показательное
распределение с параметром λ, равно M(X)=1/λ,
а дисперсия равна D(X)=1/λ2.
Доказательство.
0
0
M X x x dx x e x dx xde x
x
x
1 x
x
xe
e dx x e
0
0
e 0
0
Лекция 6. Характеристики случайных величин 39

40.

§6. Характеристики распределений
x
1
x 1
1
x x x
e 0
e 0
e 0
x 1 1
1
1
1 1
2 x
0 .
e x
x
e
0
0
M X 2 x 2 x dx x 2 e x dx x 2 de x
2
2 x
x
2
x e
2 xe x dx x x e x dx
0
e 0 0
0
Лекция 6. Характеристики случайных величин 40

41.

§6. Характеристики распределений
2
2 1
2
x
0
2
x
e
x
2x
2
2
2
2x
x
2 2
2
x
e x
e
x
2
2 2
2 x
2 2;
e x
D X M X M X
2
2
2
2
1
2
1
2
.
Лекция 6. Характеристики случайных величин 41

42.

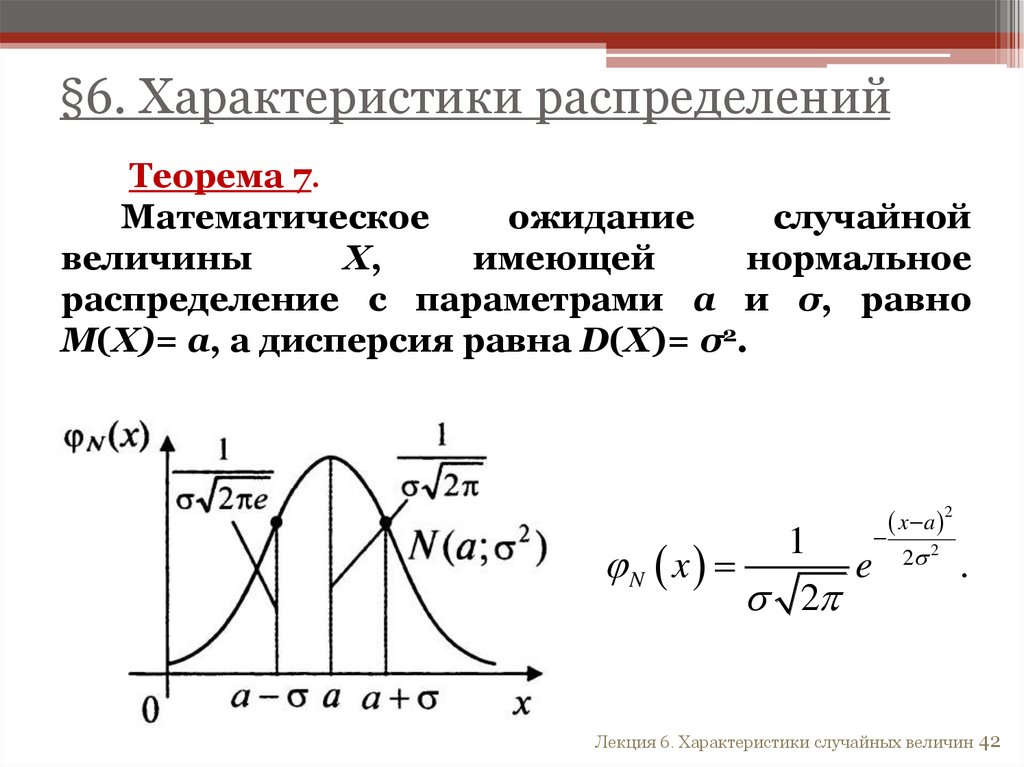
§6. Характеристики распределений
Теорема 7.
Математическое
ожидание
случайной
величины
Х,
имеющей
нормальное
распределение с параметрами a и σ, равно
M(X)= a, а дисперсия равна D(X)= σ2.
1
N x
e
2
2
x a
2 2
.
Лекция 6. Характеристики случайных величин 42

43.

ФГБОУ ВО «УлГПУ им. И.Н. Ульянова»
Теория вероятностей и математическая статистика
лектор Макеева О.В.
Продолжение следует…