Случайные информационные процессы (Лекция 7)

1.

ТЕОРИЯ
ИНФОРМАЦИИ
ДАННЫЕ
ЗНАНИЯ
Лекция 7

2.

СЛУЧАЙНЫЕ
ИНФРОМАЦИОННЫЕ
ПРОЦЕССЫ

3. Случайные процессы

• Большинство реальных информационных процессов в
той или иной степени носят случайный характер.
• Случайные процессы описываются
статистическими(вероятностными) законами.
• Пример: напряжение на входе приемника: v(t) = u(t) +
x(t)
где v(t) – регистрируемое напряжение,
u(t) – формируемый устройством первичного
сообщения сигнал (детерминированный),
x(t) – помеха измерения, имеющая случайный
характер.

4. Числовые характеристики случайных процессов

При решении многих практических задач
случайный процесс, помимо
вероятностного описания , может быть
представлен рядом неслучайных
числовых характеристик, постоянных
или изменяющихся во времени.

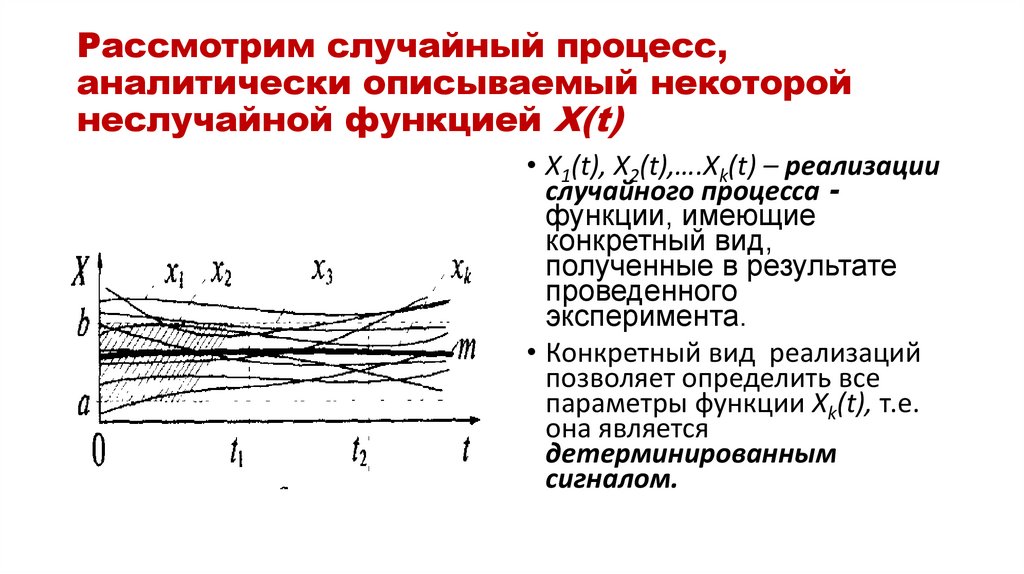
5. Рассмотрим случайный процесс, аналитически описываемый некоторой неслучайной функцией X(t)

• X1(t), X2(t),….Xk(t) – реализации
случайного процесса функции, имеющие
конкретный вид,
полученные в результате
проведенного
эксперимента.
• Конкретный вид реализаций
позволяет определить все
параметры функции Xk(t), т.е.
она является
детерминированным
сигналом.

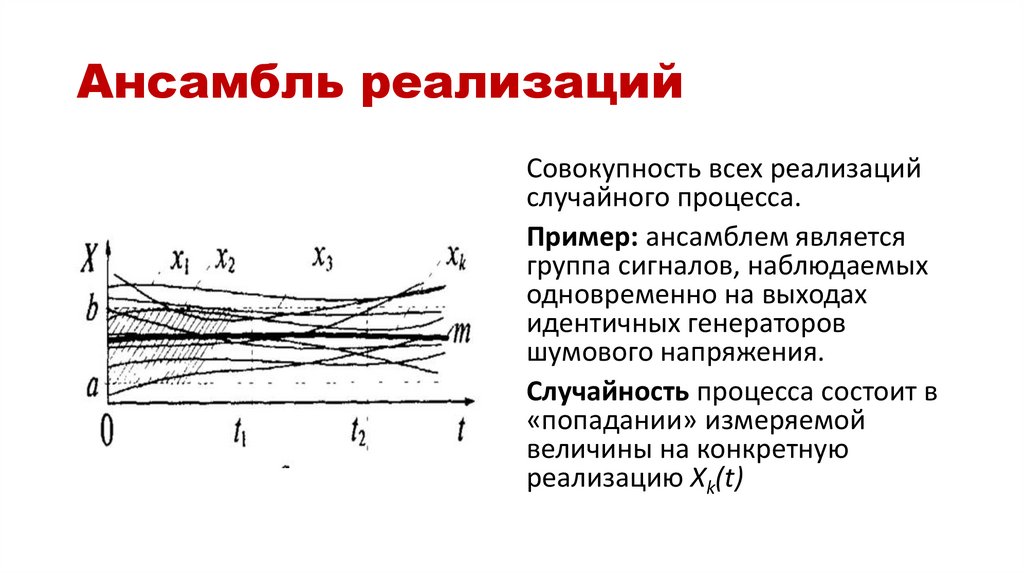
6. Ансамбль реализаций

Совокупность всех реализаций
случайного процесса.
Пример: ансамблем является
группа сигналов, наблюдаемых
одновременно на выходах
идентичных генераторов
шумового напряжения.
Случайность процесса состоит в
«попадании» измеряемой
величины на конкретную
реализацию Xk(t)

7. Сечение случайного процесса

• Выберем произвольный момент времени t1
• Совокупность отдельных мгновенных значений
всех реализаций ансамбля
X(t1)={X1( t1), X2(t1),…, Xk(t1)}
называется сечением случайного процесса
• Сечение случайного процесса является случайной
величиной.

8. Интегральная функция распределения F(x)

Численно эта функция определяется как вероятность того,
что все значения случайной величины X(t1) не
превышают некоторого заданного уровня x:
F(x) = P[X(t1) < x]
Где P – символ, характеризующий вероятность события.
Для случайной величины X(t1) , принимающей любые
вещественные значения, интегральная функция
распределения принадлежит интервалу:
0 ≤ F(x) ≤ 1

9. Плотность вероятности p( x, t1)

Если случайная функция X(t1) является
непрерывной во времени, то часто вместо
функции распределения F(x) используют её
производную
p( x, t1) = dF(x)/dx = dF/dx
p( x, t1) – одномерная плотность
распределения вероятности.

10. Зададим интервал изменения параметра х: a < x < b

Зададим интервал изменения
параметра х: a < x < b
Вероятность попадания случайной величины
X(t1) в заданный интервал a … b
p( x, t1) = F(a) - F(b) = P[a < X(t1) < b]

11. Пусть a → - ∞ , а b принимает текущее значение переменной x

• Интегральная функция распределения вероятности:
• Одномерная плотность распределения вероятности всегда
неотрицательная величина, удовлетворяющая условию:

12. Многомерная плотность распределения вероятности

• Обычно сведений, полученных с помощью одномерной
плотности распределения вероятности p( x, t1) ,
недостаточно для полного анализа развития случайного
процесса во времени.
• Исчерпывающей характеристикой случайного процесса
случит n-мерная плотность вероятности
полученная для k различных реализаций в n различных
фиксированных моментах времени.

13. Двумерная плотность вероятности p[ x( t1), x( t2)]

Для ее определения используют два сечения
случайного процесса X(t1) и X(t2) ,
полученные в разные моменты времени t1
и t2

14. Основные статистические характеристики случайных процессов (моменты)

•Математическое ожидание
•Дисперсия
•Функция корреляции

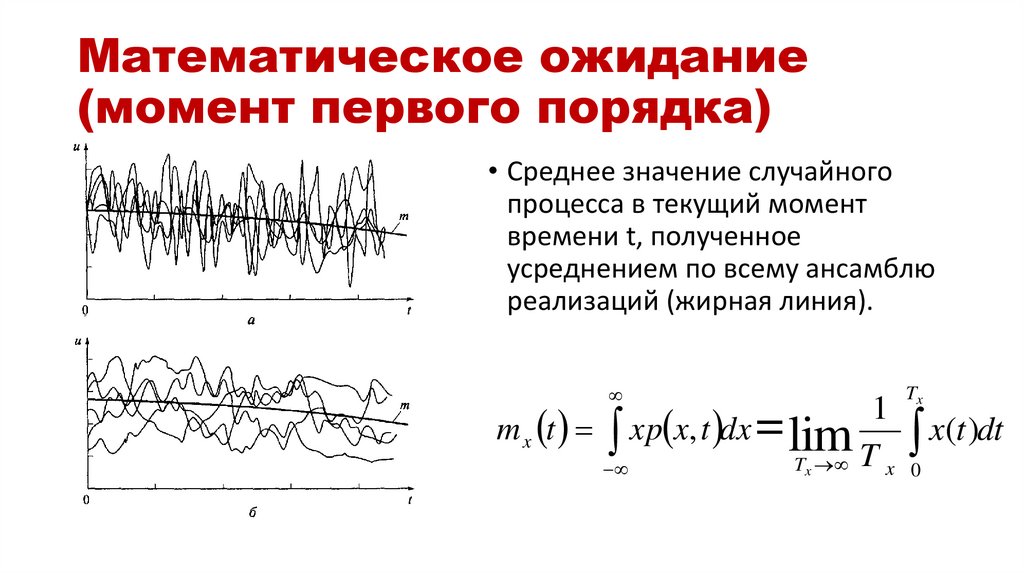
15. Математическое ожидание (момент первого порядка)

• Среднее значение случайного
процесса в текущий момент
времени t, полученное
усреднением по всему ансамблю
реализаций (жирная линия).
Tx
1
m x t xp x, t dx = lim
x(t )dt
Tx T x 0

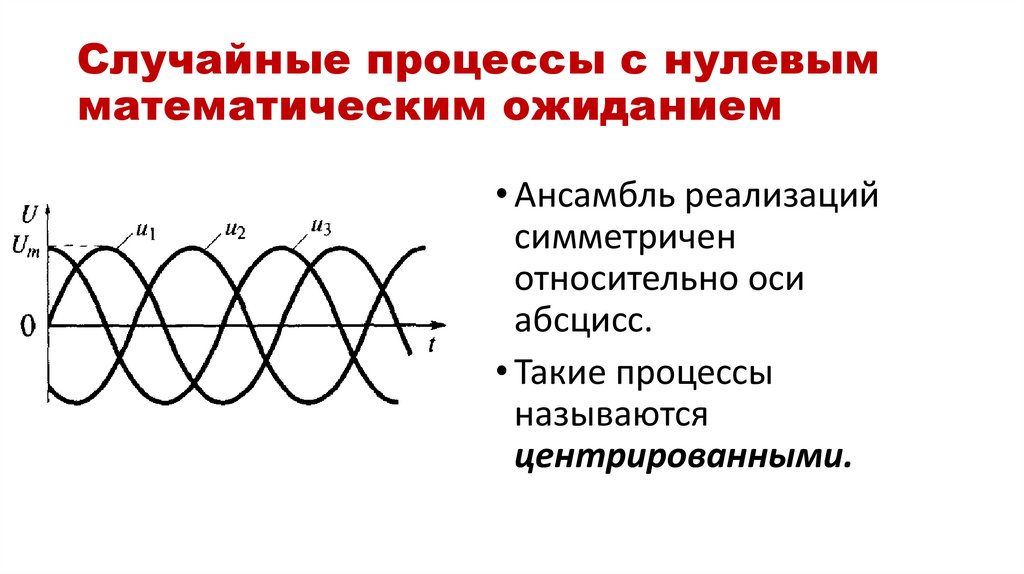
16. Случайные процессы с нулевым математическим ожиданием

• Ансамбль реализаций
симметричен
относительно оси
абсцисс.
• Такие процессы
называются
центрированными.

17. Дисперсия (момент второго порядка или среднеквадратическое отклонение)

• Характеризует разброс мгновенных значений реализаций
случайного процесса относительно его среднего значения
2
Tx
2
1
D x (t ) t x t m x t p x, t dx lim
x(t ) mx (t ) dt
Tx T x 0
2
x
• Физический смысл: действующее значение случайного
напряжерия или тока на единичном сопротивлении.

18. Функция корреляции ( двумерный центральный момент)

• Мера связи между сечениями случайного процесса, взятыми в
моменты времени t1 и t2
• Когда
t1 = t2
функция корреляции равна дисперсии

19.

Внимание!!!! Все
перечисленные числовые
характеристики являются
неслучайными функциями

20. Стационарный случайный процесс

• Процесс, статистические характеристики которого не являются
функциями времени.
m x xp( x)dx =
D x x2 ( x m2 ) 2 p( x)dx
Tx
2
1
2
2
Dx ( x m x ) p( x)dx lim
x
(
t
)
m
dt
x
(
t
)
m
x
x
T
Tx
x 0
2
x
2

21. Функция корреляции стационарного случайного процесса

• Зависит только от разности
• Из определения стационарного случайного процесса следует, что
его функция корреляции является четной относительно
R x (t , t ) R x (0) (0)
2
x

22.

Примером стационарного случайного процесса
является тепловой шум (имеется в виду тепловой
ток) транзистора, стабилитрона, диода и других
полупроводниковых и электронных приборов. На
практике условие стационарности случайного
процесса обычно ограничивается требованием
независимости от времени только одномерной и
двумерной плотностей вероятности.

23. Пример

• . Задан случайный процесс U(t), состоящий из ансамбля реализации гармонического вида
u (t ) U m cos( 0 t )
где амплитуда U m , и частота 0 — известные постоянные параметры, а
фазовый угол — случайная величина, которая с одинаковой
вероятностью может принимать любое значение в интервале от - до
• Найти числовые характеристики данного случайного процесса и
определить, является ли он стационарным?

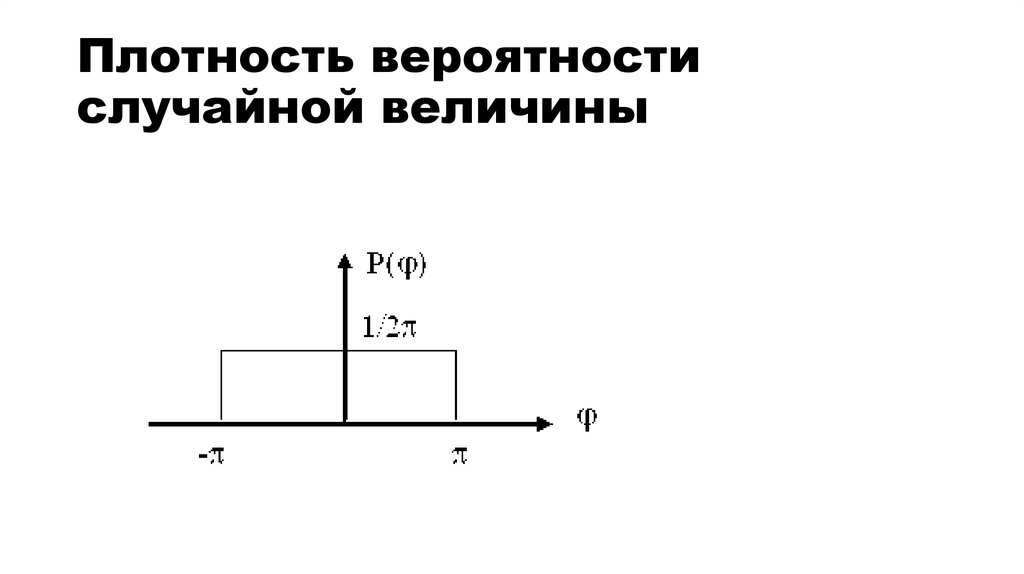
24. Плотность вероятности случайной величины

25. Решение

• Заданное в примере распределение означает, что плотность вероятности случайной фазы любого из гармонических колебаний
р( ) = 1/(2 ).
• Тогда, математическое ожидание для амплитуд гармонических
напряжений случайного процесса
Um
mx xp( x)dx
cos( 0t )d 0
2

26. Дисперсия

27. Функция корреляции

• Функцию корреляции можно получить усреднением
произведения двух сигналов
Вычисление
произведения дает следующее выражение:
Первое слагаемое в фигурных скобках является
детерминированным колебанием, так как в нем отсутствует
случайная фаза. Второе слагаемое при статистическом усреднении
по фазе с помощью одномерной плотности вероятности
обращается в нуль. Поэтому функция корреляции

28. Вопрос стационарности

все искомые числовые характеристики не
зависят от времени, и поэтому заданный
случайный процесс является стационарным.

29. Эргодический стационарный случайный процесс

• Случайный процесс, у которого усреднение по
ансамблю реализаций можно заменить
усреднением по времени одной реализации в
пределах бесконечно длинного интервала

30. Основные статистические характеристики стационарного эргодического случайного процесса

• Математическое ожидание
• Дисперсия
• Функция корреляции
Tx
1
x(t )dt
Tx Tx 0
mx x(t ) lim