Similar presentations:
Математические основы теории систем
1. Математические основы теории систем
Каплун Дмитрий Ильич2. МОТС
• Лекции- контрольные работы (баллы)
- экзамен
• Практика
- лабораторные работы (баллы+зачёт)
3. Мотс Лекции
• Математическая статистика и основыстатистической обработки сигналов
• Основы спектрального анализа
• Основы цифровой обработки сигналов
• Постановка задачи оптимизации
• Квадратичное и линейное
программирование
4. МОТС Практика
• Основы математическогомоделирования
• Основы моделирования в среде Matlab
• Лабораторные работы
5. МОТС Лабораторные работы
• Матричные преобразования и трёхмернаяграфика
• Статистическая обработка сигналов и
корреляционный анализ
• Спектральный анализ и ряд Фурье
• Цифровые фильтры
• Квадратичное и линейное
программирование
6. МОТС Лабораторные работы
Методические указания в электронном виде
Задание
Выполнение в Matlab
Отчёт по электронной почте на e-mail:
dikaplun@etu.ru
Одобрение
• Распечатка
• Защита
Неодобрение
• Исправление ошибок
• Повторная отсылка
7. МОТС Случайные процессы
• Случайным процессом (СП) называетсяфункция времени ξ t , значение которой в
любой момент времени есть случайная
величина (СВ)
• Случайные процессы – частный случай
случайных функций ξ x , значения которых
для каждого x есть случайная величина.
• СП являются как информационные сигналы,
используемые для передачи сообщений
(речь, музыка, изображение), так и помехи, с
которыми взаимодействует полезный сигнал
при передаче по каналу связи и усилении
слабого принятого сигнала
8. МОТС Случайная величина
• СВ является обобщением понятия случайногособытия, при котором каждому элементарному
событию ставится в соответствие
некоторое
ω
ξ f ω
число
.
• Пусть рассматриваемая величина принимает
значения из множества X, которое может быть
конечно X =
, счетно
x; x1 , x2 ,
, xn X =
континуально
X =, причем
x; x a, b
x; x1или
, x2 ,
, x n ,
возможны случаи
,a . b
• СВ, для которой X – конечное или счетное
множество, называется дискретной.
9. МОТС Случайная величина
• Дискретную СВ можно полностью определить,задав распределение вероятностей, т. е.
совокупность пар чисел pi , xi , где xi –
значение СВ, а pi – вероятность этого
значения.
• Универсальным способом описания СВ любой
природы является задание функции
распределения (ФР), определяемой как
вероятность события, состоящего в том, что СВ ξ
будет меньше значения x, являющегося
аргументом функции распределения, т. е.
Fξ x P ξ x .
10. Свойства функций распределения
1. Fξ x – неотрицательная неубывающая функция.2. Функция Fξ x непрерывна слева, что символически
можно записать как
Fξ x – Fξ x =00.
3. Функция распределения позволяет определить
вероятность попадания СВ
x1,как
x2
ξв интервал
P x1 x2 = F x 2 F x1.
4. Функция F xтерпит
разрыв первого рода при тех
ξ
значения х, которые принимаются СВ с конечной
вероятностью 0<p<1. Величина скачка в точке разрыва
равна вероятности p. Функция распределения может
иметь не более чем счетное множество скачков.
5. Значения
на левой и правой границах множества
X как вероятности невозможного и достоверного
Fξ x соответственно нулю и единице.
событий равны
Поэтому,
=0и
= 1.
F
F
11. Функции распределения
На рис. 1 приведены ФР для СВ дискретного (а),непрерывного (б) и смешанного (в) типов.
1
1
б
а
1
в
Рис. 1
12. Плотность вероятности
• Случайная величина называетсянепрерывной (относится к классу, типу
непрерывных СВ), если существует
неотрицательная функция W ,x
удовлетворяющая при любых xξравенству
F x =
ξ
x
W y dy , а
ξ
W x
dF x .
dx
• Функция
называется
плотностью
Wξ x
вероятности (ПВ).
13. Свойство плотности вероятности
1. W x 02. При любых x1, x2 X справедливо
равенство
x2
Px2 x1 x2 F x2 F x1 W x dx .
x1
3. Следствием свойства 2 является
условие нормировки
W x dx F F 1
14. Примеры распределений Распределение Бернулли
W x 1 p δ x p δ x 10
1
а
1
0, x 0;
F x 1 p,0 x 1;
1, x 1,
0
1
б
Рис. 2
15. Примеры распределений Биномиальное распределение
• К биномиальному распределению мы приходим,рассматривая схему последовательных независимых
испытаний. Предполагается, что испытания
проводятся в неизменных условиях, вероятность
успеха в каждом испытании равна p и не зависит от
результатов предшествующих испытаний.
• Пусть проведено N испытаний и нас интересует,
какова вероятность того, что успех имел место ровно
M раз, где 0 M N .
N
M M
F x C N
p 1 p N M 1 x M
M 0
N
M M
W x C N
p 1 p N M δ x M
M 0
16. Примеры распределений Равномерное распределение
A, x a, b ;W x
0, x a, b .
0
а
1
0, x a;
x a
F x
, a x b;
b a
1, x b.
0
б
Рис. 3
17. Примеры распределений Нормальное (гауссовское) распределение
W x0
а
1
2 σ 2
e
x a 2
2σ2
х
а
x
1
F x
0,5
0
а
б
Рис. 4
х
1
2
e
t a 2
2 σ 2 dt
2 σ
x a
z2
σ
x a
e 2
1
2
σ
18. МОТС Случайные процессы
Случайным процессом (t) называется функция двухаргументов (t, ), где , – множество
элементарных событий; t T, T – область
определения функций (t, ). При фиксированном
значении t (t, ) является случайной величиной, а
для каждого фиксированного (заданного
элементарного события) (t, ) зависит только от t и
определяет реализацию СП (траекторию,
выборочную функцию). Как и для СВ, область
значений (t, ) может быть счетным (в том числе и
конечным) и континуальным множеством Ф.
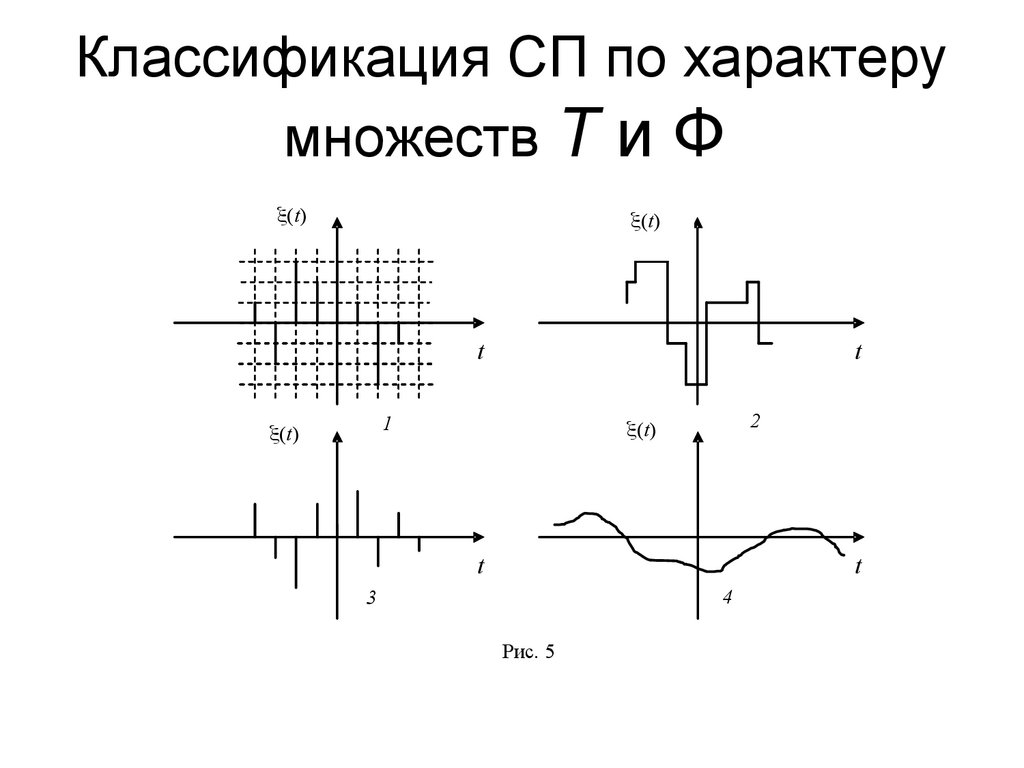
19. Классификация СП
Классификацию СП можно осуществить по характерумножеств Т и Ф и виду статистической связи между
значениями СП, соответствующими различным
моментам времени t T.
В зависимости от характера множеств Т и Ф случайные
процессы можно разделить на четыре класса (примеры
их реализаций приведены на рис. 5, 1 – 4
соответственно):
• процессы с дискретными состояниями и дискретным
временем (дискретные случайные последовательности);
• процессы с дискретными состояниями и непрерывным
временем (дискретные СП);
• процессы с непрерывными состояниями и дискретным
временем (случайные последовательности);
• процессы с непрерывными состояниями и непрерывным
временем.
20. Классификация СП по характеру множеств Т и Ф
(t)(t)
t
t
1
(t)
2
(t)
t
t
4
3
Рис. 5
21. Классификация СП по виду статистической связи между значениями СП
• Для классификации СП по виду статистическойсвязи между значениями СП нам потребуется
ввести полное статистическое описание
случайного процесса. Говорят, что имеется
полное статистическое описание СП (t), если
для любых n и t1, t2, …, tn T можно задать
функцию распределения:
n
F x1 , x 2 , , x n ; t1 , t 2 , , t n P (ti ) xi
i 1
• При этом должно быть выполнено условие
симметрии и условие согласованности.
22. Статистическое описание СП Условия симметрии и согласованности СП
• Условие симметрииF x1, x2 , , xn ; t1, t 2 , , t n F xi1 , xi2 , , xin ; ti1 , ti2 , , tin
где i1, i2, …, in – перестановка чисел 1, 2, …, n.
• Условие согласованности
F x1, , xi 1, , xi 1, , xn ; t1, t 2 , , ti 1, ti , ti 1, , t n
F x1, , xi 1, xi 1, , xn ; t1, t 2 , , ti 1, ti 1, , t n
для любых i.
23. Статистическое описание СП
Наиболее часто для описания СП используют:• математическое ожидание (среднее
значение) случайного
процесса (t)
m1 (t ) mx xW ( x; t ) dx , где t T
• корреляционную функцию
K (t1, t 2 ) M 11 (t1, t 2 ) x1 m1 (t1 ) x2 m1 (t 2 ) W ( x1, x2 ; t1, t 2 ) dx1dx2
где t1, t2 T .
Можно ввести коэффициент корреляции:
,где М2(t1) и М2(t2) – дисперсии
отсчетов процесса в моменты времени t1 и t2.
24. Статистическое описание СП
• Если имеется два случайных процесса(t) и (t), то можно ввести в
рассмотрение взаимную
корреляционную функцию:
25. Классификация СП по вероятностным характеристикам
• Наиболее простым с точки зрения вероятностногоописания будет СП, у которого любая совокупность
значений (отсчетов), взятых в произвольные
моменты времени, принадлежащие множеству Т,
независима, т. е.
• Существуют СП, у которых статистические связи
распространяются лишь на два соседних отсчета. К
их числу относится марковский процесс, для
которого
26. Стационарный СП
• Случайный процесс (t) называетсястрого стационарным (стационарным
в узком смысле), если его ФР, ПВ или
ХФ при любых , п и t1, t2, …, tn T
инвариантны к сдвигу моментов t1, t2, …,
tn на величину , т. е.
.
27. Стационарный СП
СП называется стационарным в широком смысле (по Хинчину),если выполняются более скромные требования:
1.среднее значение процесса m1(t) не зависит от времени, т. е.
m1(t) = const;
2.КФ K (t1, t2) зависит лишь от разности t1– t2 = , т. е.
K (t1, t2) = K (t1– t2) = K ( ).
•Из второго условия следует, что дисперсия стационарного
процесса D (t) = K (t, t) = K (0) = const.
•В силу симметрии K (t1, t2) корреляционная функция
стационарного СП является четной функцией:
K (– ) = K ( ).
28. Стационарный СП
Стационарный в узком смысле процесс называетсяэргодическим, если любые его вероятностные
характеристики, найденные на основе статистического
усреднения, по множеству реализаций с вероятностью,
сколь угодно близкой к единице, совпадают с
соответствующими средними по времени. Иными
словами, если известна одна-единственная реализация
процесса для
, то путем сдвигов по времени
может быть получен бесконечный статистический
ансамбль реализаций. Следовательно, по одной
реализации можно узнать всевозможные
вероятностные характеристики .
29. Эргодический СП
Эргодичность процесса можно определить наоснове условной ПВ . Для стационарного в узком
смысле процесса одномерная ПВ W (x0; t) не
зависит от времени, а двумерная W (x1, x2; t1, t2)
зависит только от разности t1 - - t2 = , поэтому
условная ПВ
для стационарного процесса будет равна
и будет зависеть только от t1 –
t2 = .
Если
и не зависит от х1,
то процесс (t) называется эргодическим.
30. Эргодический СП
Иными словами, требуется, чтобы отсчетыстационарного процесса в любые моменты
времени t1 и t2 при t1– t2 становились бы
независимыми. Для нормального случайного
процесса, ПВ отсчетов которого задается
многомерным нормальным распределением,
это условие выполняется, если корреляционная
функция стремится к нулю, когда , т. е.
K ( ) = 0.
31. Свойства эргодических СП
Для эргодического процесса имеет место важноесвойство, используемое для экспериментального
определения ПВ и ФР. Оно связано с временем
пребывания эргодического процесса между двумя
уровнями х1 и х2
.
Предел отношения
при Т равен вероятности
попадания отсчетов СП в промежуток (х1, х2), т. е.
Если х1 – х2 = х достаточно мало, то Р(х1<x<х2)=
=W (x) x и
При х1 = – получаем возможность для оценки ФР, так
как Р( < x < х2) = F(x2)
32. Свойства эргодических СП
x(t)x2
x1
t1
t2
ti
t3
T
Рис. 6
t
33. Квазидетерминированный СП
Квазидетерминированный процессопределяется как совокупность функций
времени t заданного вида
, зависящих от
случайного параметра
–
случайного вектора. Иногда такие СП называют
элементарными случайными функциями.
Например,
, где А, , –
случайные величины с совместной ПВ W ( А,
, ).
34. Случайные процессы
На рис. 7 приняты следующие обозначения: 1 –нестационарные СП; 2 – стационарные в широком
смысле СП; 3 – стационарные в узком смысле СП; 4 –
эргодические СП; 5 – квазидетерминированные СП; 6 –
СП с независимыми значениями; 7 – марковские СП; 8 –
СП с независимыми приращениями.

































 mathematics
mathematics








