Similar presentations:
Статистическая радиотехника. Случайный процесс, ансамбль его реализаций
1. Курс лекций по дисциплине «СТАТИСТИЧЕСКАЯ РАДИОТЕХНИКА»
Лектор - Куроедов СергейКонстантинович
Лекция 4
2. ПЛАН ЛЕКЦИИ 4
1. Случайный процесс, ансамбль егореализаций, сечение случайного процесса и
сечение ансамбля реализаций
2. Характеристики распределений и
моментные функции случайных процессов
3. Стационарные и эргодические случайные
процессы
4. Спектральные характеристики
стационарных случайных процессов,
теорема Винера-Хинчина
5. Равенство Парсеваля
3. ХАРАКТЕРИСТИКИ СЛУЧАЙНЫХ ПРОЦЕССОВ
Случайный процесс – это случайнаяфункция времени z(t), значения
которой в любой момент времени из
области ее определения являются
случайными величинами (априорно
неизвестны)
Множество X(t) = {x1(t), x2(t),…, xn(t)}
реализаций xi(t) случайного процесса
z(t) называется ансамблем
реализаций данного процесса
4. ХАРАКТЕРИСТИКИ СЛУЧАЙНЫХ ПРОЦЕССОВ
Случайная величина z(t1),представленная мгновенными
значениями случайного процесса z(t)
в фиксированный момент времени t1,
называется сечением случайного
процесса
Множество X(t1) = {x1(t1), x2(t1),…,
xn(t1)} мгновенных значений xi(t1)
реализаций случайного процесса z(t)
в фиксированный момент времени t1
называется сечением ансамбля
реализации случайного процесса
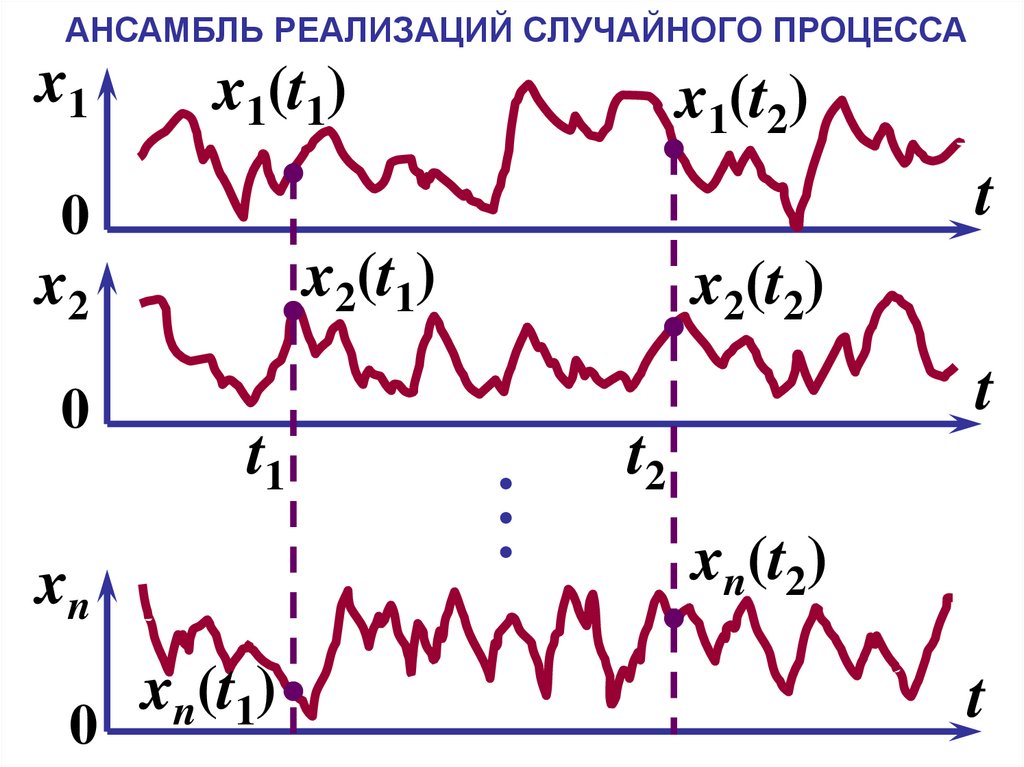
5. АНСАМБЛЬ РЕАЛИЗАЦИЙ СЛУЧАЙНОГО ПРОЦЕССА
x1x1(t1)
x1(t2)
t
0
x2(t1)
x2
0
t
xn(t1)
...
t1
xn
0
x2(t2)
t2
xn(t2)
t
6. ХАРАКТЕРИСТИКИ СЛУЧАЙНЫХ ПРОЦЕССОВ
Одномерная функция распределениявероятностей F(x,t1) случайного
процесса z(t) – функция
распределения вероятностей
сечения z(t1):
F ( x, t1) P z(t1) x
7. ХАРАКТЕРИСТИКИ СЛУЧАЙНЫХ ПРОЦЕССОВ
Одномерная плотностьвероятности p(x,t1) случайного
процесса z(t) – плотность
вероятности сечения z(t1):
P x z (t1 ) x x
p( x, t1 ) lim
x 0
x
8. ХАРАКТЕРИСТИКИ СЛУЧАЙНЫХ ПРОЦЕССОВ
Двумерная функция распределениявероятностей F(x1,x2,t1,t2)
случайного процесса z(t):
F ( x1 , x2 , t1 , t2 )
P z (t1 ) x1 , z (t2 ) x2
9. ХАРАКТЕРИСТИКИ СЛУЧАЙНЫХ ПРОЦЕССОВ
Двумерная плотностьвероятности p(x,t1) случайного
процесса z(t):
p ( x1 , x2 , t1 , t2 )
P x1 z (t1 ) x1 x1 , x2 z (t2 ) x2 x2
lim
x1 0
x1 x2
x 0
2
Многомерная плотность
вероятности случайного процесса:
p( x1, x2 ,..., xn , t1, t2 ,..., tn )
10. МОМЕНТНЫЕ ФУНКЦИИ СЛУЧАЙНЫХ ПРОЦЕССОВ
Математическое ожидание –первый момент сечения z(t),
характеризует среднее значение
случайного процесса в момент
времени t :
m1 (t ) x(t )
xp
(
x
,
t
)
dx
11. МОМЕНТНЫЕ ФУНКЦИИ СЛУЧАЙНЫХ ПРОЦЕССОВ
Дисперсия – второй центральныймомент сечения z(t), характеризует
среднее значение квадрата
флуктуаций случайного процесса в
момент времени t :
(t ) x(t ) m1 (t )
2
2
x
x
m
(
t
)
1
2
p( x, t )dx
12. МОМЕНТНЫЕ ФУНКЦИИ СЛУЧАЙНЫХ ПРОЦЕССОВ
Функция корреляции (функцияавтокорреляции, корреляционная
функция, автокорреляционная
функция) – второй центральный
смешанный момент сечений z(t1) и
z(t2), характеризует корреляцию или
среднюю взаимную мощность
флуктуаций случайного процесса в
моменты времени t1 и t2
13. ФУНКЦИЯ КОРРЕЛЯЦИИ
Rx (t1 , t2 ) [ x(t1 ) m1 (t1 )][ x(t2 ) m1 (t2 )][
x
(
t
)
m
(
t
)
][
x
(
t
)
m
(
t
)]
1
1
1
2
1
2
p( x1 , x2 , t1 , t2 )dx1dx2
При совмещении сечений z(t1) и z(t2)
Rx (t , t ) [ x(t ) m1 (t )] (t )
2
2
x
14. СТАЦИОНАРНЫЕ СЛУЧАЙНЫЕ ПРОЦЕССЫ
Случайный процесс называетсястационарным в узком смысле, если
его любые многомерные плотности
вероятности инвариантны
относительно временного сдвига τ:
p( x1 , x2 ,..., xn , t1 , t2 ,..., tn )
p( x1 , x2 ,..., xn , t1 , t2 ,..., tn )
15. СТАЦИОНАРНЫЕ СЛУЧАЙНЫЕ ПРОЦЕССЫ
Любые моментные функциистационарных в узком смысле
случайных процессов,
определяемые по одному сечению,
не зависят от времени:
mn (t ) mn
Моментные функции, определяемые
по двум сечениям, зависят только от
разности временных аргументов
16. СТАЦИОНАРНЫЕ СЛУЧАЙНЫЕ ПРОЦЕССЫ
Случайный процесс называетсястационарным в широком смысле,
если его, по крайней мере,
одномерные и двумерные плотности
вероятности инвариантны
относительно временного сдвига τ
Моментные функции первого и
второго порядка стационарного в
широком смысле случайного
процесса либо не зависят от
времени, либо зависят только от
разности временных аргументов
17. МОМЕНТНЫЕ ФУНКЦИИ СТАЦИОНАРНЫХ СЛУЧАЙНЫХ ПРОЦЕССОВ
m1 (t ) m1Rx (t1, t2 ) Rx ( ), t2 t1
Rx ( ) [ x(t1 ) m1 ][ x(t2 ) m1 )]
[ x(t2 ) m1 ][ x(t1 ) m1 )] Rx ( )
Функция корреляции стационарного
случайного процесса - четная
18. МОМЕНТНЫЕ ФУНКЦИИ СТАЦИОНАРНЫХ СЛУЧАЙНЫХ ПРОЦЕССОВ
[ x(t ) m1 ] [ x(t ) m1 )]2
[ x(t ) m1 ] 2[ x(t ) m1 ][ x(t ) m1 )]
[ x(t ) m1 )] 2 2 Rx ( ) 0
2
2
x
Rx ( ) Rx (0)
2
x
Функция корреляции стационарного
случайного процесса имеет
максимум в нуле
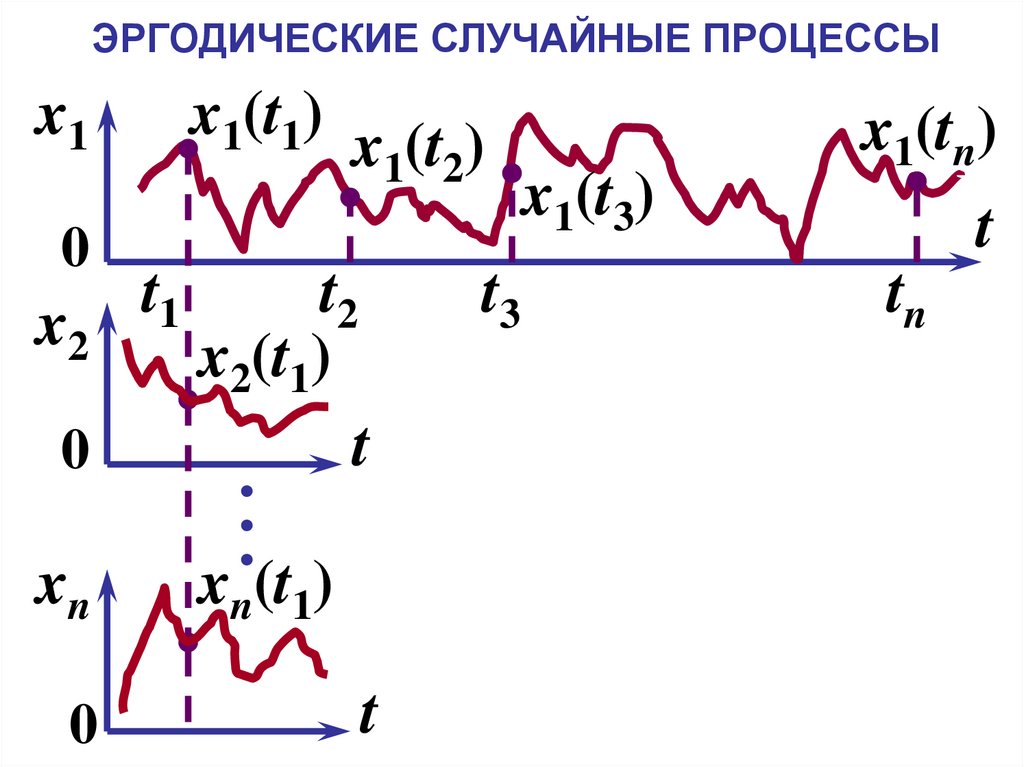
19. ЭРГОДИЧЕСКИЕ СЛУЧАЙНЫЕ ПРОЦЕССЫ
Стационарный случайный процессназывается эргодическим, если
усреднение любой его
вероятностной характеристики по
ансамблю реализаций эквивалентно
усреднению во времени по одной из
реализаций
Условие эргодичности:
lim Rx ( ) 0
20. ЭРГОДИЧЕСКИЕ СЛУЧАЙНЫЕ ПРОЦЕССЫ
x10
x2
0
0
t1
x1(t2)
t2
x2(t1)
t
...
xn
x1(t1)
xn(t1)
t
t3
x1(t3)
x1(tn)
t
tn
21. МОМЕНТНЫЕ ФУНКЦИИ ЭРГОДИЧЕСКИХ СЛУЧАЙНЫХ ПРОЦЕССОВ
Математическоеожидание:
T
1
m1 lim x(t )dt
T T
0
Дисперсия:
T
1
2
lim [ x(t ) m1 ] dt
T T
0
2
x
22. МОМЕНТНЫЕ ФУНКЦИИ ЭРГОДИЧЕСКИХ СЛУЧАЙНЫХ ПРОЦЕССОВ
Функция корреляции :T
1
Rx ( ) lim [ x(t ) m1 ][ x(t ) m1 ]dt
T T
0
Значение функции корреляции
характеризует корреляционную связь
между двумя сечениями случайного
процесса, разделенными временным
промежутком длительностью τ
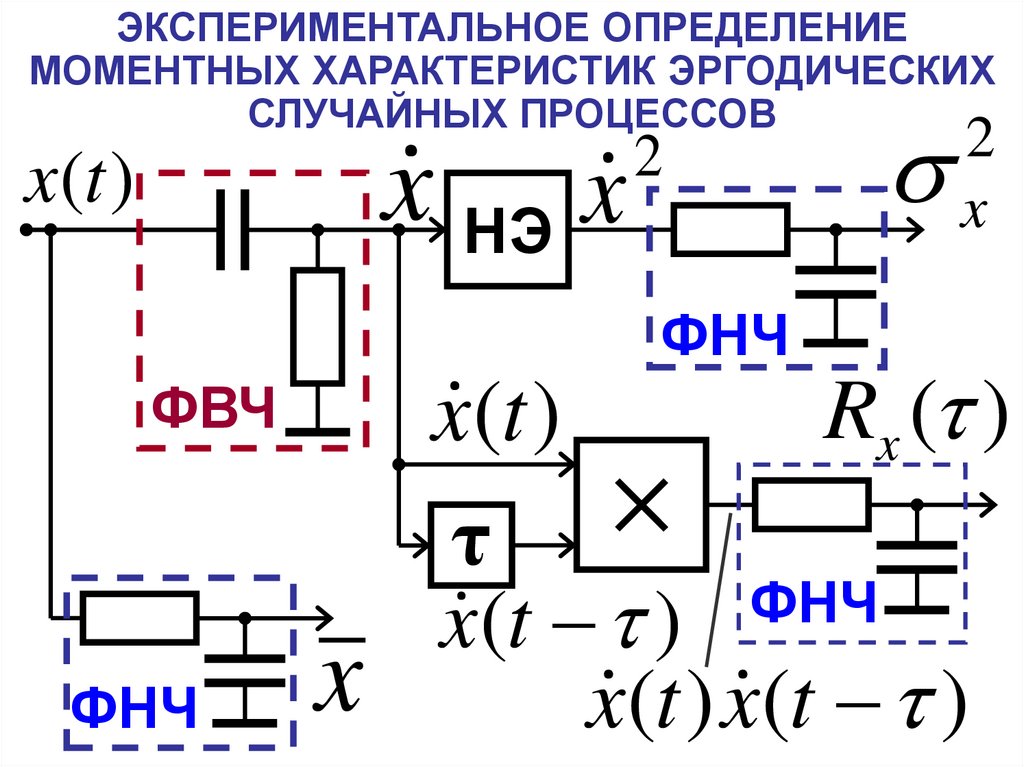
23. ЭКСПЕРИМЕНТАЛЬНОЕ ОПРЕДЕЛЕНИЕ МОМЕНТНЫХ ХАРАКТЕРИСТИК ЭРГОДИЧЕСКИХ СЛУЧАЙНЫХ ПРОЦЕССОВ
x НЭ xx(t )
2
ФНЧ
ФВЧ
ФНЧ
x
2
x
Rx ( )
x (t )
τ
x(t ) ФНЧ
x (t ) x (t )
24. СПЕКТРАЛЬНЫЕ ХАРАКТЕРИСТИКИ СТАЦИОНАРНЫХ СЛУЧАЙНЫХ ПРОЦЕССОВ
S(ω) - спектральная плотностьреализации x(t) стационарного
случайного процесса z(t):
S ( ) x(t )
1
x(t )
2
S
(
)
e
d
j t
25. СПЕКТРАЛЬНЫЕ ХАРАКТЕРИСТИКИ СТАЦИОНАРНЫХ СЛУЧАЙНЫХ ПРОЦЕССОВ
Математическое ожиданиестационарного случайного
процесса:
1
x(t )
2
S
(
)
e
d
m
1
j t
Математическое ожидание
спектральной плотности как
случайной функции частоты:
S ( ) 2 m1 ( )
26. СПЕКТРАЛЬНЫЕ ХАРАКТЕРИСТИКИ СТАЦИОНАРНЫХ СЛУЧАЙНЫХ ПРОЦЕССОВ
S ( ) 0, ( , ), 0Спектральная плотность
стационарного случайного процесса
является случайной функцией
частоты, математическое
ожидание которой при любом
значении частоты, кроме нулевого,
равно нулю
27. ТЕОРЕМА ВИНЕРА-ХИНЧИНА
ST(ω) – спектральная плотностьреализации x(t) случайного процесса
на интервале длительностью T:
ST ( )
T
2
e
)
t
(
x
T
2
T
j t
dt
ST ( ) S ( ) ST ( )
2
28. ТЕОРЕМА ВИНЕРА-ХИНЧИНА
ST ( ) ST ( ) S ( )T
2
T
2
x
(
t
)
e
1
T
2
dt1 x(t2 )e
T T
2 2
j t1
T
2
x
(
t
)
x
(
t
)
e
1
2
T T
2 2
j t 2
dt2
T
2
j ( t2 t1 )
dt1dt2
29. ТЕОРЕМА ВИНЕРА-ХИНЧИНА
t2 t1 , dt2 dST ( )
x(t1 ) x(t2 ) Rx ( ), lim
W ( )
T
T
t2 t1 , dt2 d
2
ST ( )
x(t1 ) x(t2 ) Rx ( ), lim
W ( )
T
T
W ( )
R
(
)
e
x
j
2
d
30. ТЕОРЕМА ВИНЕРА-ХИНЧИНА
Спектральная плотностьмощности случайного процесса
определяется математическим
ожиданием суммарной мощности его
спектральных составляющих на
частотном интервале шириной в 1 Гц
1
Rx ( )
2
W
(
)
e
j
d
31. ТЕОРЕМА ВИНЕРА-ХИНЧИНА
1j
d
e
)
(
W
Rx ( )
2
W ( ) R ( )e j d
x
32. ТЕОРЕМА ВИНЕРА-ХИНЧИНА
Спектральная плотностьмощности и функция корреляции
стационарного случайного процесса
связаны между собой парой
преобразований Фурье
Rx ( ) W ( )
33. РАВЕНСТВО ПАРСЕВАЛЯ
1Rx (0)
2
2
x
W
(
)
d
Средняя мощность (дисперсия)
стационарного случайного процесса
равна сумме средних мощностей
(дисперсий) всех спектральных
составляющих данного процесса
34. СВОЙСТВА СПЕКТРА МОЩНОСТИ
• Спектр мощности W(ω) действительная, неотрицательнаяфункция частоты, определенная на
всей числовой прямой
• Спектр мощности W(ω) – четная
функция частоты: W(-ω) = W(ω)
1
Rx ( )
2
1
W
(
)
e
j
W
(
)
cos(
)
d
0
d
35. ОДНОСТОРОННИЙ СПЕКТР МОЩНОСТИ
F ( ) 0, 0W ( )
F
(
)
,
0
Rx ( ) F ( )cos( )d
0
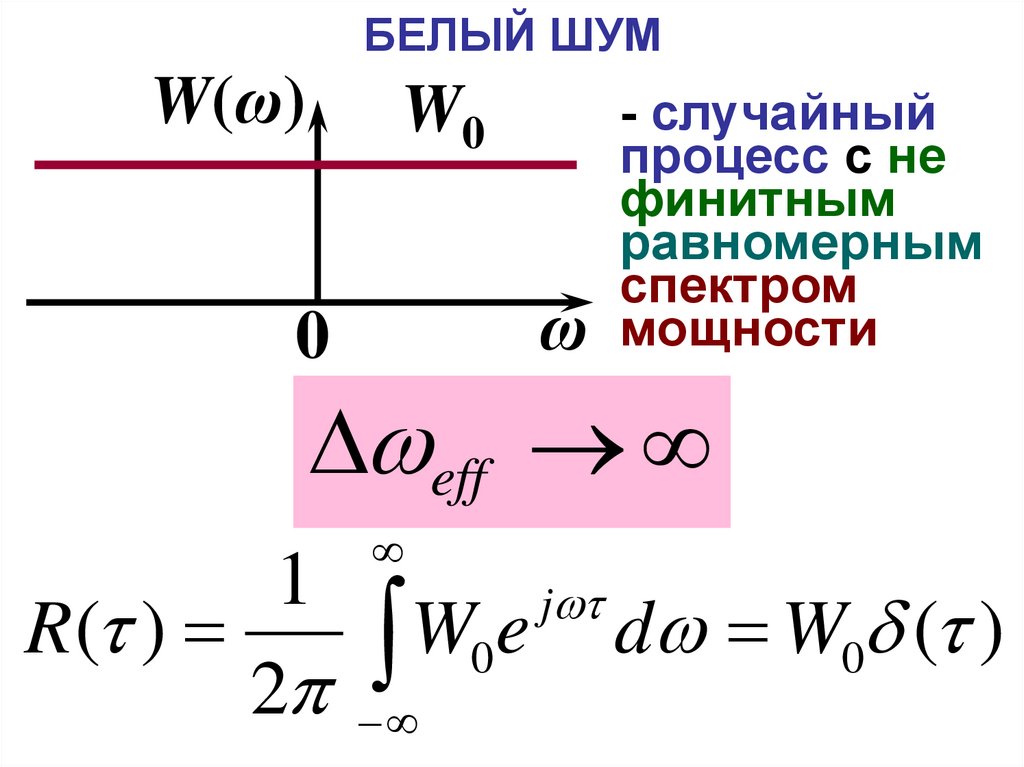
36. БЕЛЫЙ ШУМ
W(ω)W0
ω
0
- случайный
процесс с не
финитным
равномерным
спектром
мощности
eff
1
R( )
2
W
e
0
j
d W0 ( )
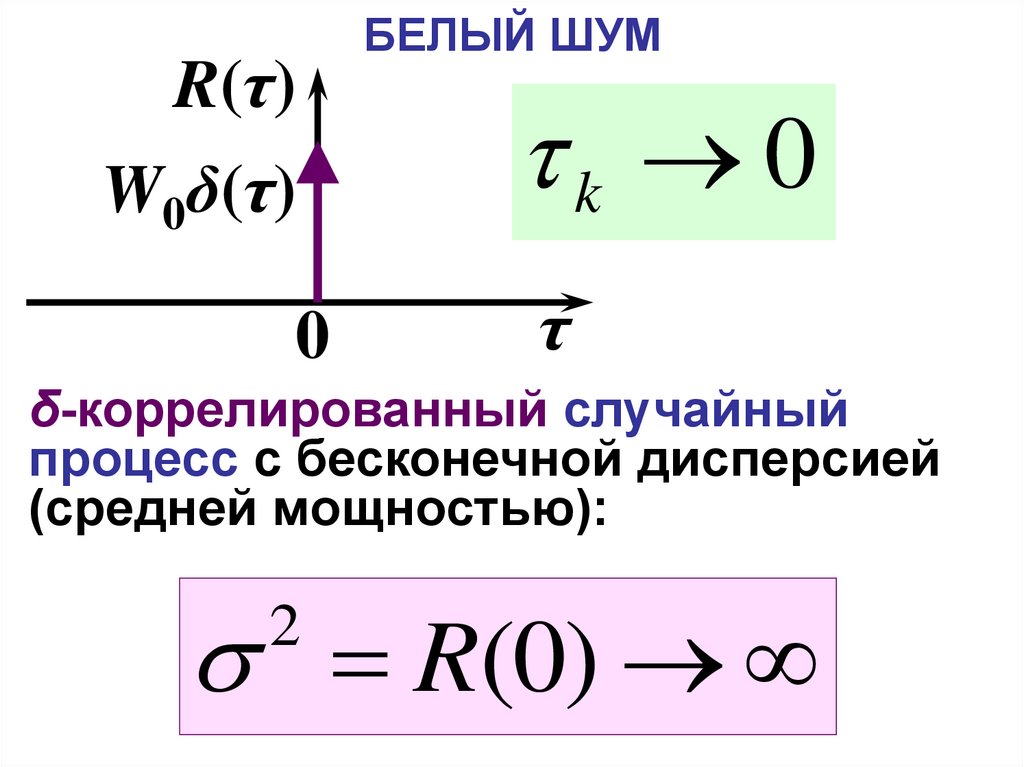
37. БЕЛЫЙ ШУМ
R(τ)W0δ(τ)
0
БЕЛЫЙ ШУМ
k 0
τ
δ-коррелированный случайный
процесс с бесконечной дисперсией
(средней мощностью):
R(0)
2
































 mathematics
mathematics physics
physics








