Similar presentations:
Статистическая радиотехника. Узкополосный случайный процесс
1. Курс лекций по дисциплине «СТАТИСТИЧЕСКАЯ РАДИОТЕХНИКА»
Лектор - Куроедов СергейКонстантинович
Лекция 1-5
2. ПЛАН ЛЕКЦИИ 1-5
1. Узкополосный случайный процесс(УСП), функция корреляции УСП
2. Спектральные и корреляционные
характеристики сопряженных УСП
3. Корреляционные свойства синфазных
и квадратурных амплитуд УСП
4. Характеристики нормальных УСП,
распределение Релея
5. Характеристики суммы гармонического
колебания и нормального УСП,
распределение Райса
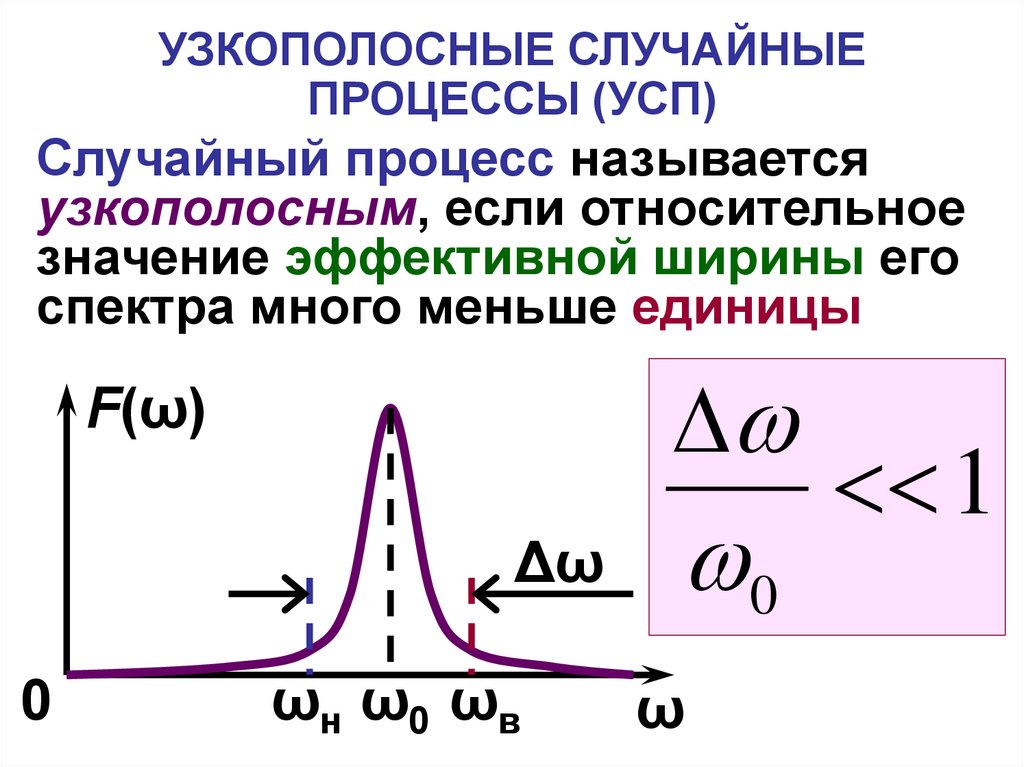
3. УЗКОПОЛОСНЫЕ СЛУЧАЙНЫЕ ПРОЦЕССЫ (УСП)
Случайный процесс называетсяузкополосным, если относительное
значение эффективной ширины его
спектра много меньше единицы
F(ω)
Δω
0
ωн ω0 ωв
0
ω
1
4. ФУНКЦИЯ КОРРЕЛЯЦИИ УСП
Теорема Винера-Хинчина:R( ) F ( )cos( )d
0
Замена частотной переменной:
0 , 0
5. ФУНКЦИЯ КОРРЕЛЯЦИИ УСП
R( ) a( )cos( ) b( ) sin( )a(τ) - огибающая синфазной
составляющей R(τ):
a( )
F
(
)
cos(
)
d
0
0 ( )
6. ФУНКЦИЯ КОРРЕЛЯЦИИ УСП
b(τ) - огибающая квадратурнойсоставляющей R(τ):
b( )
F
(
)
sin
(
)
d
0
0 ( )
Условие симметричности спектра
мощности относительно частоты ω0:
F ( 0 ) F ( 0 ) b( ) 0
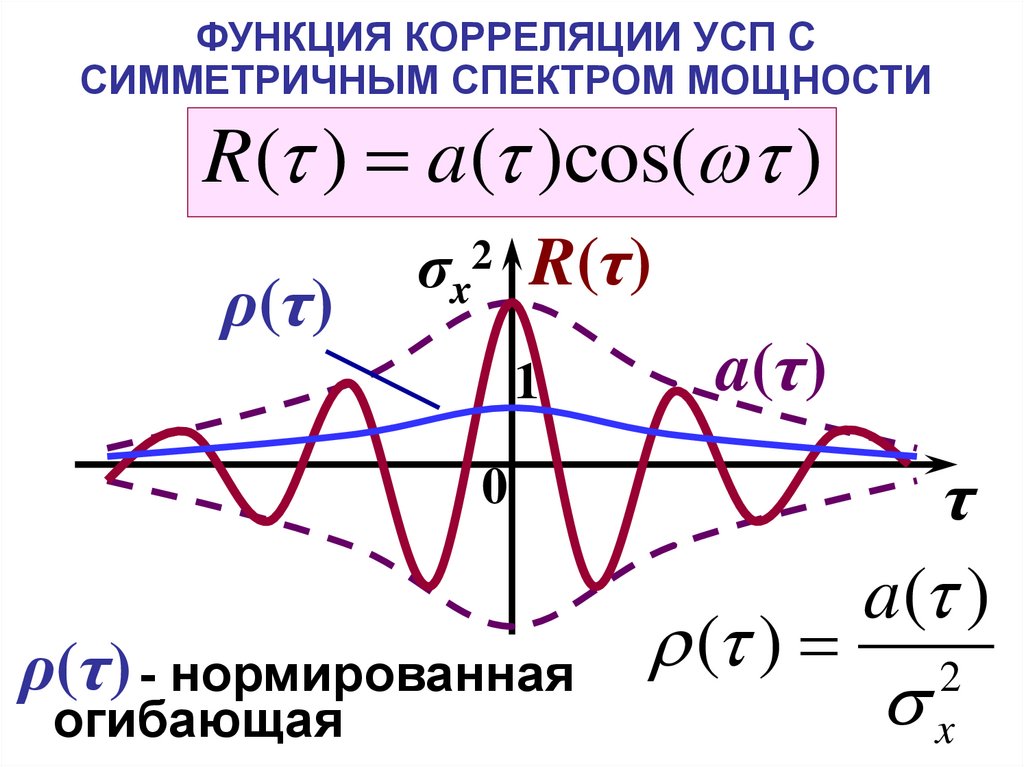
7. ФУНКЦИЯ КОРРЕЛЯЦИИ УСП С СИММЕТРИЧНЫМ СПЕКТРОМ МОЩНОСТИ
R( ) a( )cos( )ρ(τ)
σx2 R(τ)
1
a(τ)
τ
0
ρ(τ) - нормированная
огибающая
( )
a ( )
2
x
8. СПЕКТРАЛЬНЫЕ И КОРРЕЛЯЦИОННЫЕ ХАРАКТЕРИСТИКИ УСП
Реализации сопряженных поГильберту УСП:
x(t ) A(t )cos( 0t ) B(t ) sin( 0t )
y (t ) xˆ (t ) H[ x(t )]
y (t ) B(t )cos( 0t ) A(t ) sin( 0t )
9. СПЕКТРАЛЬНЫЕ И КОРРЕЛЯЦИОННЫЕ ХАРАКТЕРИСТИКИ УСП
Спектральные плотности реализацийсопряженных по Гильберту УСП:
S x ( ) x(t ), S y ( ) y(t )
S y ( ) j sign( ) S x ( )
S x ( ) S y ( )
10. СПЕКТРАЛЬНЫЕ И КОРРЕЛЯЦИОННЫЕ ХАРАКТЕРИСТИКИ УСП
Спектры мощности сопряженных поГильберту УСП:
Wx ( ) Wy ( )
Функции корреляции сопряженных
по Гильберту УСП:
Rx ( ) Ry ( )
11. ФУНКЦИЯ ВЗАИМНОЙ КОРРЕЛЯЦИИ СОПРЯЖЕННЫХ УСП
Rxy ( ) x(t ) y (t )x( )
x(t )
d
t
1
x(t ) x( )
d
t
1
12. ФУНКЦИЯ ВЗАИМНОЙ КОРРЕЛЯЦИИ СОПРЯЖЕННЫХ УСП
Rx ( t )Rxy ( )
d
( t )
1
Функция взаимной корреляции
сопряженных УСП сопряжена по
Гильберту с функцией корреляции
УСП:
Rxy ( ) H [ Rx ( )]
13. ФУНКЦИЯ ВЗАИМНОЙ КОРРЕЛЯЦИИ СОПРЯЖЕННЫХ УСП
Rxy ( ) Fx ( ) sin ( )d0
Rxy ( ) a( ) sin ( 0 ) b( ) cos( 0 )
Свойства функции взаимной
корреляции сопряженных УСП :
1. Нечетность:
Rxy ( ) Rxy (- )
14. СВОЙСТВА ФУНКЦИИ ВЗАИМНОЙ КОРРЕЛЯЦИИ СОПРЯЖЕННЫХ УСП
2. Некоррелированностьсопряженных УСП в совмещенных
сечениях:
Rxy (0) 0
3. Свойство перестановки:
Rxy ( ) Ryx ( )
15. КОРРЕЛЯЦИОННЫЕ СВОЙСТВА СИНФАЗНОЙ И КВАДРАТУРНОЙ АМПЛИТУД УСП
Реализации сопряженных поГильберту УСП:
x(t ) A(t )cos( 0t ) B(t ) sin( 0t )
y
(
t
)
B
(
t
)
cos(
t
)
A
(
t
)
sin(
t
)
0
0
Синфазная и квадратурные
амплитуды реализации УСП:
A(t ) x(t )cos( 0t ) y (t ) sin( 0t )
B(t ) x(t ) sin ( 0t ) y (t )cos( 0t )
16. ФУНКЦИЯ КОРРЕЛЯЦИИ СИНФАЗНОЙ АМПЛИТУДЫ УСП
1RA ( ) A(t ) A(t ) cos( 0 )
2
1
[ x(t ) x(t ) y (t ) y (t )]
2
sin ( 0 )[ x(t ) y (t ) y (t ) x(t )]
RA ( ) Rx ( ) cos( 0 ) Rxy ( ) sin( 0 )
17. КОРРЕЛЯЦИОННЫЕ СВОЙСТВА СИНФАЗНОЙ И КВАДРАТУРНОЙ АМПЛИТУД УСП
RA ( ) a( ), RA ( ) a( )RAB ( ) b( )
Дисперсии синфазной и
квадратурной амплитуд УСП:
a(0)
2
A
2
B
2
x
18. ХАРАКТЕРИСТИКИ НОРМАЛЬНЫХ УСП
1p ( x)
e
2 x
x
2
2
2 x
Синфазная и квадратурная
амплитуды нормального УСП
распределены по закону Гаусса
19. ХАРАКТЕРИСТИКИ НОРМАЛЬНЫХ УСП
Двумерная плотность вероятностинормальных синфазной и
квадратурной амплитуд УСП:
p( A, B) p( A) p( B)
p( A)
1
2 A
e
A
2
2
2
A
20. ХАРАКТЕРИСТИКИ НОРМАЛЬНЫХ УСП
p( B)p( A, B)
1
2 B
1
e
B
2
2 B
e
2
2 x
2
A B
2
2
2 x
2
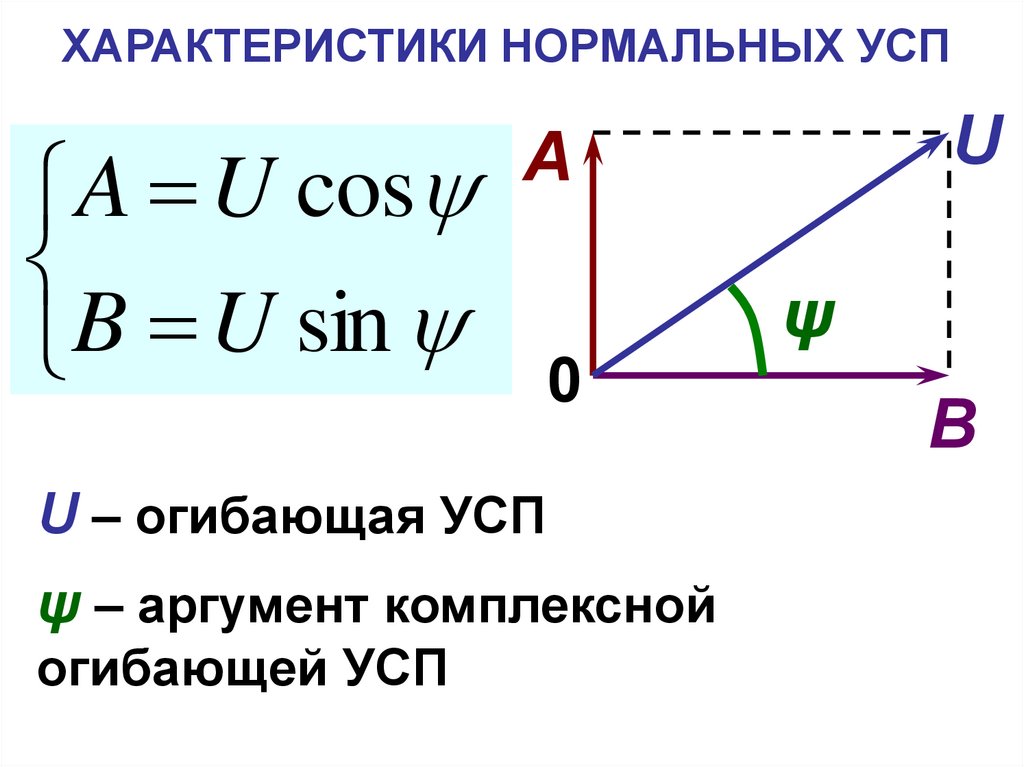
21. ХАРАКТЕРИСТИКИ НОРМАЛЬНЫХ УСП
A U cosB
U
sin
ψ
0
U – огибающая УСП
ψ – аргумент комплексной
огибающей УСП
U
A
B
22. ЯКОБИАН ОБРАТНОГО ПРЕОБРАЗОВАНИЯ
AU
D
B
U
A
B
cos
U sin
sin
U cos
U
23. ДВУМЕРНАЯ ПЛОТНОСТЬ ВЕРОЯТНОСТИ ОГИБАЮЩЕЙ И ФАЗЫ УСП
p (U , ) p ( A, B ) DU
2
2
x
e
U
2
2
2 x
24. ПЛОТНОСТЬ ВЕРОЯТНОСТИ ФАЗЫ УСП
p ( ) p (U , )dU0
1 U
e
2
2 0 x
U
2
2
2 x
1
dU
2
25. ПЛОТНОСТЬ ВЕРОЯТНОСТИ ФАЗЫ УСП
p(ψ)1/2π
ψ
-π
0
π
Фаза УСП распределена равномерно
на интервале (-π, π)
26. ПЛОТНОСТЬ ВЕРОЯТНОСТИ ОГИБАЮЩЕЙ УСП
p (U )p
(
U
,
)
d
U
e
2
2 x
U
2
2
2 x
d
U
e
2
x
U
2
2
2 x
27. ПРОИЗВЕДЕНИЕ ПЛОТНОСТЕЙ ВЕРОЯТНОСТ ФАЗЫ И ОГИБАЮЩЕЙ УСП
1 Up( ) p(U )
2e
2 x
U2
2
2 x
p(U , )
Модуль и аргумент комплексной
огибающей УСП статистически
независимы
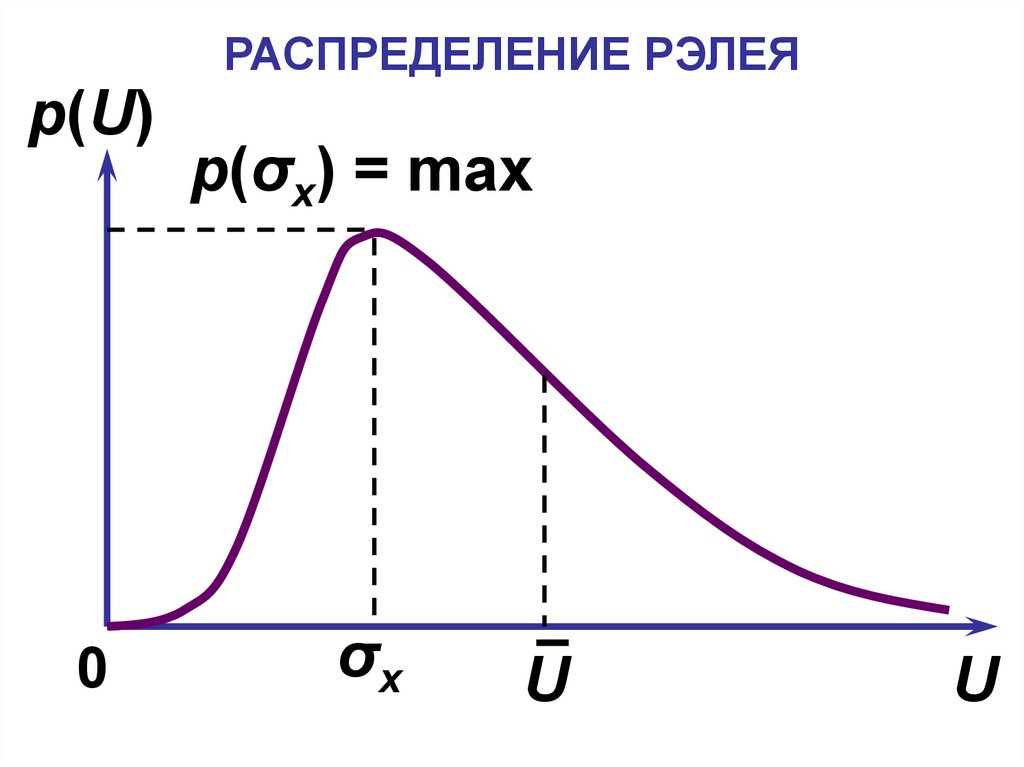
28. РАСПРЕДЕЛЕНИЕ РЭЛЕЯ
p(U)0
p(σx) = max
σx
U
U
29. РАСПРЕДЕЛЕНИЕ РЭЛЕЯ
• мода U = σx - максимумраспределения
p( x )
• математическое
ожидание
огибающей
U
1
x e
2
x
30. РАСПРЕДЕЛЕНИЕ РЭЛЕЯ
• средний квадратU 2
2
2
x
• дисперсия
U U 2
2
2
U
2
2
2
x
31. ДВУМЕРНОЕ РАСПРЕДЕЛЕНИЕ РЭЛЕЯ
UUp (U , U ) 4
e
2
x (1 )
UU
J 0 2
2
(
1
)
x
U U
2
2
2
2
2 x (1 )
32. ФУНКЦИЯ КОРРЕЛЯЦИИ ОГИБАЮЩЕЙ НОРМАЛЬНОГО УСП
RU ( ) UU U UU p (U , U )dUdU2
0 0
2
2
2 2
[( 2n 3)!!] 2 n
x x 2n
2
2
2 4 n 2 2 (n!)
rU ( )
RU ( )
2
U
0,914 ( ) 0,058 ( )
2
4
33. ВЕРОЯТНОСТНЫЕ ХАРАКТЕРИСТИКИ СУММЫ ГАРМОНИЧЕСКОГО КОЛЕБАНИЯ И НОРМАЛЬНОГО УСП
y (t ) U m cos 0t x(t )U m A(t ) cos 0t B(t ) sin 0t
U (t ) cos[ 0t (t )]
A U cos U m
B
U
sin
34. ЯКОБИАН ОБРАТНОГО ПРЕОБРАЗОВАНИЯ
AU
D
B
U
A
B
cos
U sin
sin
U cos
U
35.
p (U , ) p ( A, B ) DU
A B
2
2
2 x
e
2
2 x
U
e
2
2 x
2
U
2
2
U m
2U mU cos
2
2 x
36. ПЛОТНОСТЬ ВЕРОЯТНОСТИ ОГИБАЮЩЕЙ
p (U )p
(
U
,
)
d
2
U U m
2
2 x
2
U
2
x
e
UU m
J 0 2
x
37. МОДИФИЦИРОВАННАЯ ФУНКЦИЯ БЕССЕЛЯ
1J 0 x
2
e
x cos
d
UU m 1
J 0 2
2
x
e
UU m cos
2
x
d
38. РАСПРЕДЕЛЕНИЕ РАЙСА
p(U )U
e
2
x
U 2 U m2
2
2 x
UUm
J 0 2
x
РАСПРЕДЕЛЕНИЕ РЭЛЕЯ
Um
x
0, p(U )
U
e
2
x
U
2
2
2 x
39. НОРМАЛИЗАЦИЯ ОГИБАЮЩЕЙ
1x
x 1, J 0 ( x)
e
2 x
Um
1
1, p(U )
e
x
2 x
U U m 2
2
x
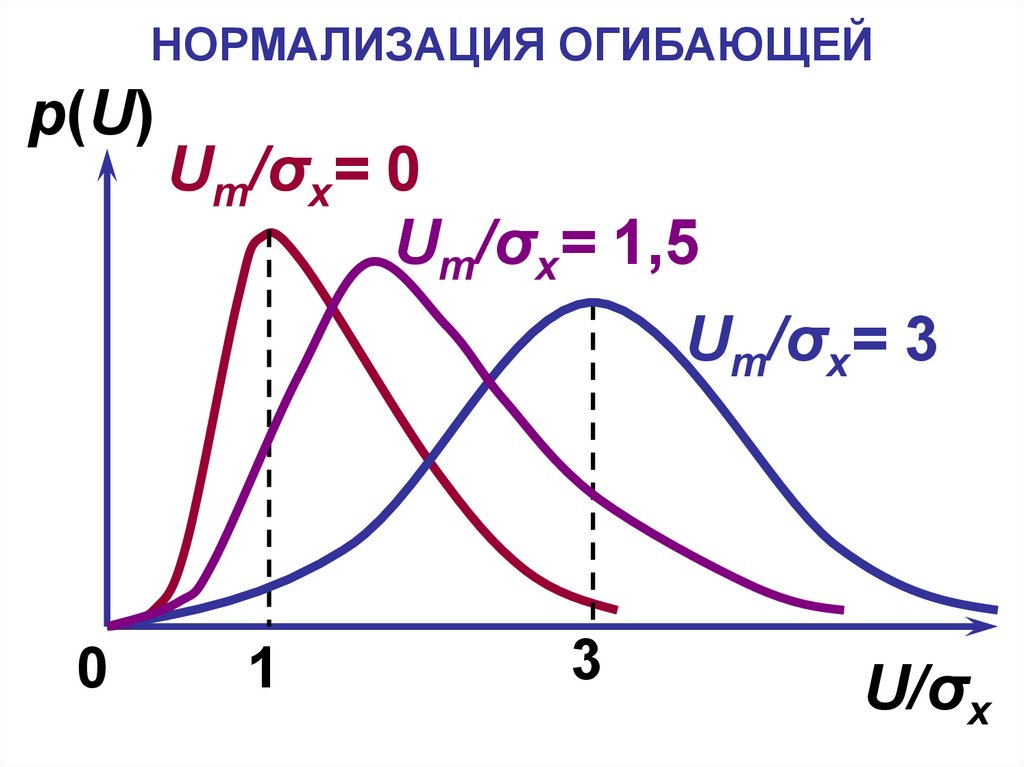
40. НОРМАЛИЗАЦИЯ ОГИБАЮЩЕЙ
p(U)Um/σx= 0
Um/σx= 1,5
Um/σx= 3
0
1
3
U/σx






























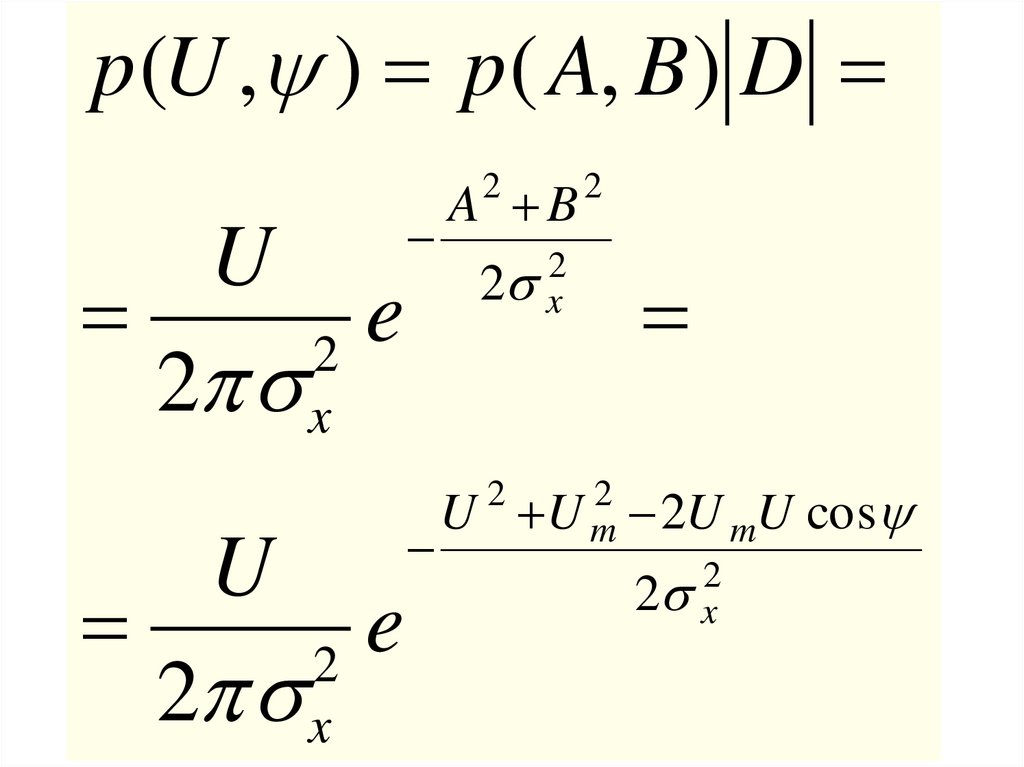




 physics
physics electronics
electronics








