Рекуррентные оптимальные алгоритмы фильтрации случайных процессов. Фильтр Калмана-Бьюси

1.

Методы обработки навигационной измерительной
информации
Автор: д.т.н., профессор Степанов Олег Андреевич
Неделя 10
Рекуррентные оптимальные
алгоритмы фильтрации случайных
процессов. Фильтр Калмана-Бьюси
Санкт-Петербург, 2016

2. На предыдущих лекциях мы обсудили вопросы дискретной фильтрации случайных последовательностей

Настоящая лекция посвящена вопросам непрерывной
фильтрации случайных процессов
x(t)
Модель измерений
y(t) = H(t)x(t) + v(t)
.
Формирующий фильтр
x(t)= F (t)x(t) + G(t)v(t)
1. Описание и свойства случайных последовательностей.
2. Дискретный фильтр Калмана.
3. Фильтр Калмана-Бьюси.
4. Дискретизация непрерывных систем.

3. Содержание

Случайные процессы и методы их описания.
Понятие формирующего фильтра и его свойства.
Постановка и общее решение задачи оптимальной
линейной фильтрации. Фильтр Калмана-Бьюси.
Связь непрерывных
фильтрации.
и
дискретных
алгоритмов

4. Случайные процессы и методы их описания

5. Определение случайного процесса

Случайные процессы и методы их описания
Определение случайного процесса
Случайным процессом x(t) в скалярном случае называется такая функция
времени t, значение которой при любом фиксированном времени t
является случайной величиной.
Корреляционная функция случайного процесса
k x (t1 , t2 ) ( x(t1 ) x (t1 ))( x(t2 ) x (t2 )) т f ( x1, t1, x2 , t2 )dx1dx2 .
(1)
Стационарным процессом в широком смысле называется такой процесс,
у которого математическое ожидание от времени не зависит, а
корреляционная функция зависит от разности аргументов
x (t ) x ; k (t2 t1 ) E{( x(t2 ) x )( x(t1 ) x )}.
(2)

6. Экспоненциально-коррелированный процесс

Случайные процессы и методы их описания
Экспоненциально-коррелированный процесс
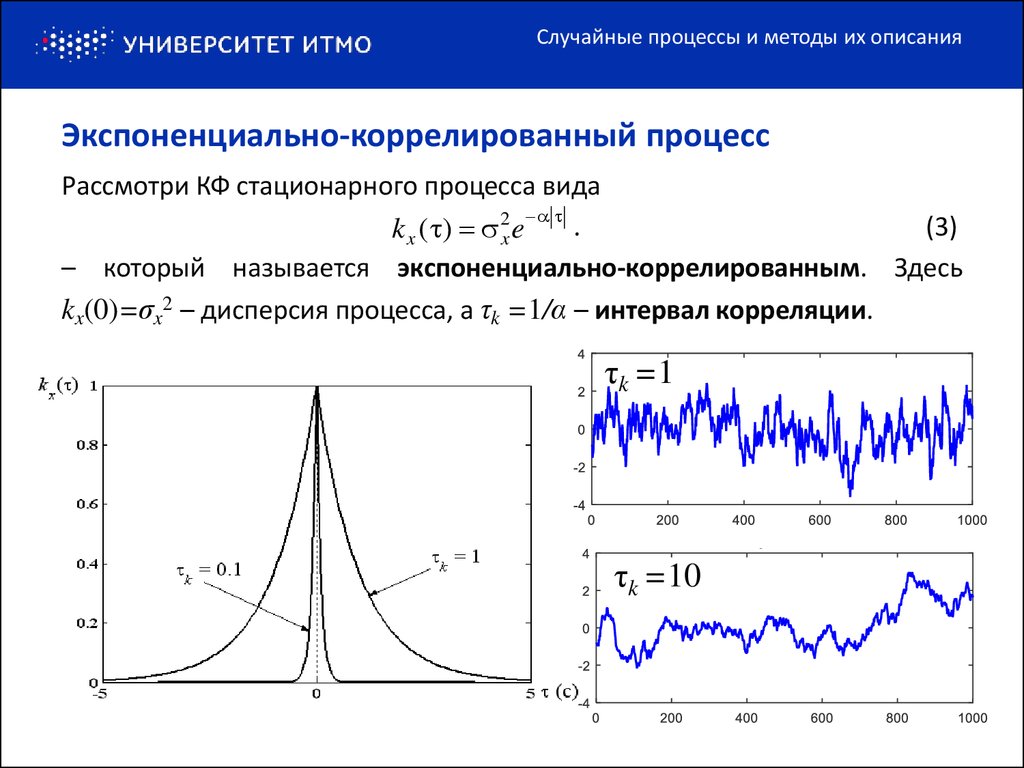
Рассмотри КФ стационарного процесса вида
.
(3)
k x ( ) 2x e
– который называется экспоненциально-коррелированным. Здесь
kx(0)=σx2 – дисперсия процесса, а τk =1/α – интервал корреляции.
τk =1
τk =10

7. Спектральная плотность случайного процесса

Случайные процессы и методы их описания
Спектральная плотность случайного процесса
Спектральная плотность также используется для описания стационарных
процессов и представляет собой преобразование Фурье от КФ
S x ( )
k ( ) exp( j )d
.
x
(4)
Справедливо и обратное представление
1
k x ( )
2
S ( ) exp( j )d .
x
(5)
В силу четного характера функций Sx (ω) и kx(τ), приведенные
соотношения можно записать:
S x ( )
1
k x ( )
2
k ( )cos d 2 k ( )cos d ;
x
x
0
1
S ( )cos d S ( )cos d .
x
(6)
x
0
(7)

8. Пример

Случайные процессы и методы их описания
Пример
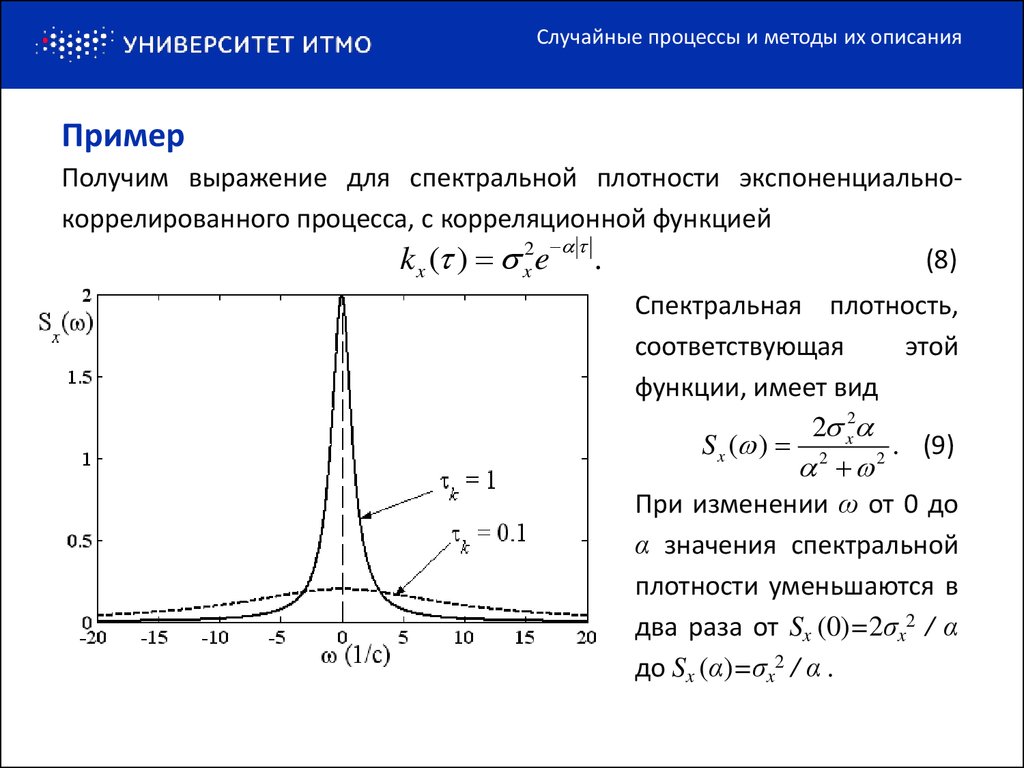
Получим выражение для спектральной плотности экспоненциальнокоррелированного процесса, с корреляционной функцией
(8)
k x ( ) x2e .
Спектральная плотность,
соответствующая
этой
функции, имеет вид
2 x2
S x ( ) 2
. (9)
2
При изменении ω от 0 до
α значения спектральной
плотности уменьшаются в
два раза от Sx (0)=2σx2 / α
до Sx (α)=σx2 / α .

9. Свойство спектральной плотности

Случайные процессы и методы их описания
Свойство спектральной плотности
1
2
S
(
)
d
k
(
0
)
x
x
x
2
(10)
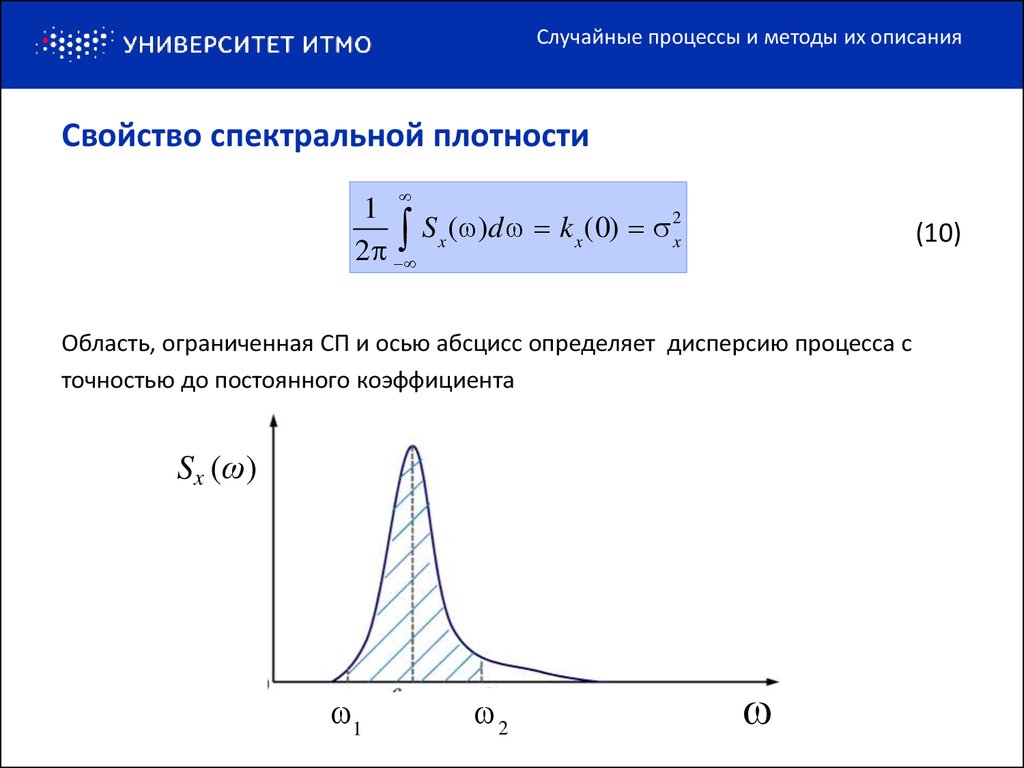
Область, ограниченная СП и осью абсцисс определяет дисперсию процесса с
точностью до постоянного коэффициента
Sx (ω)
1
2

10. Белый шум

Случайные процессы и методы их описания
Белый шум
Процесс с постоянной спектральной плотностью во всем диапазоне
частот, для которого Sx (ω)=Q, называется белым шумом (БШ). Величина
Q называется интенсивностью БШ.
Корреляционная функция БШ имеет вид
(11)
k x ( ) Q ( ),
вид который вытекает из следующего представления о дельта-функции
1
j
e
d ( ).
2
(12)
Особенности БШ:
- дисперсия БШ бесконечна;
- значения процесса в разные моменты времени не коррелированны.

11. Примеры графиков корреляционных функций и спектральных плотностей простейших процессов

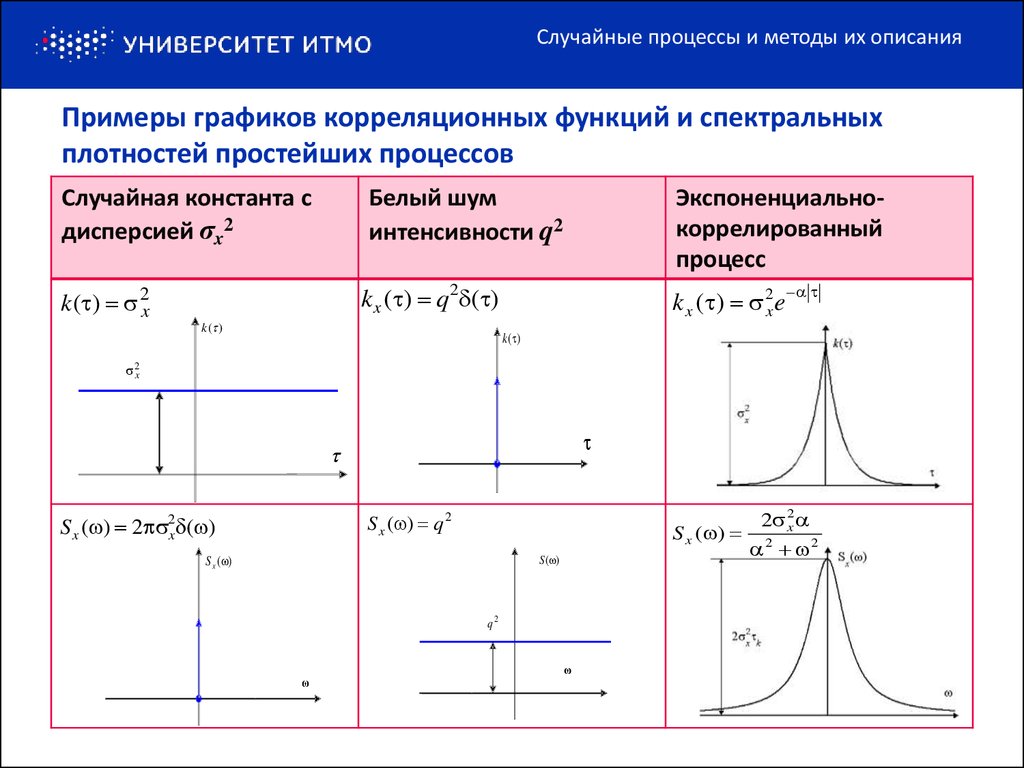
Случайные процессы и методы их описания
Примеры графиков корреляционных функций и спектральных
плотностей простейших процессов
Случайная константа с
дисперсией σx2
k ( ) 2x
Белый шум
интенсивности q2
Экспоненциальнокоррелированный
процесс
k x ( ) q 2 ( )
k ( )
k x ( ) 2x e
k ( )
2x
2 2x
S x ( ) 2
2
S x ( ) q 2
S x ( ) 2 2x ( )
S ( )
S x ( )
q2
ω
ω