Similar presentations:
Корреляционная функция случайного процесса
1.
Корреляционная функцияслучайного процесса
m1 0
σ1 1
а)
3
x1(t)
10
20
30
40
t, мкс
–3
m2 0
σ2 1
б)
3
x2 (t)
10
20
30
40
t, мкс
–3
Реализации двух случайных процессов с одинаковой плотностью
вероятности, но различной скоростью протекания
Корреляционная функция характеризует скорость
протекания случайного процесса
2.
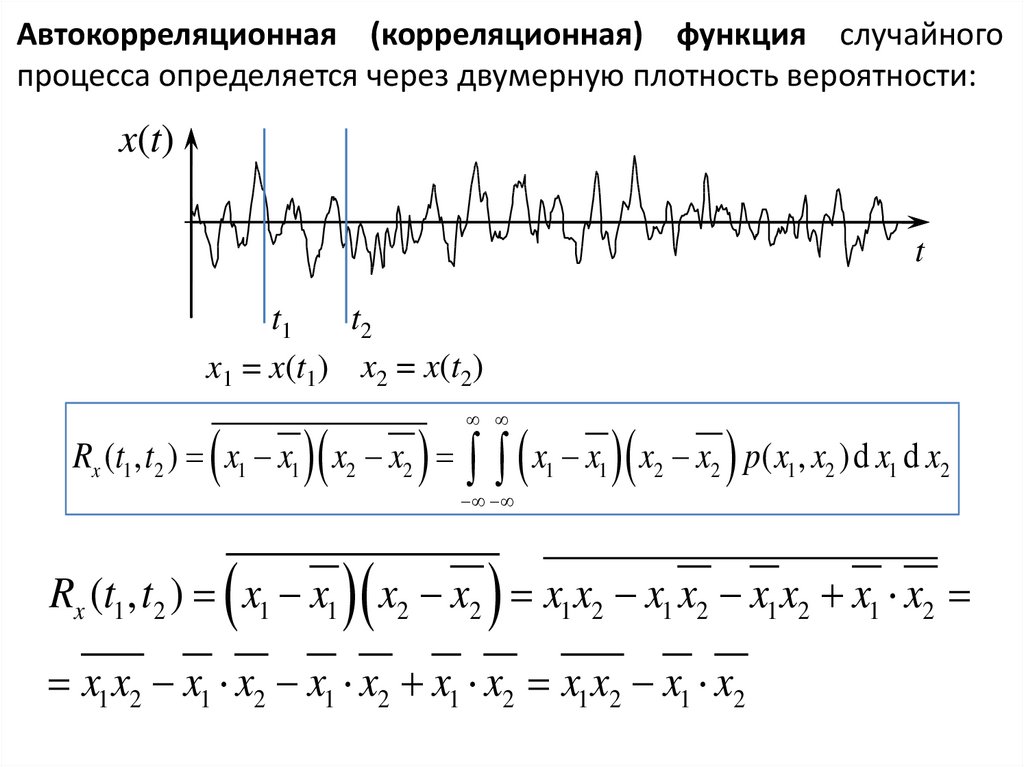
Автокорреляционная (корреляционная) функция случайногопроцесса определяется через двумерную плотность вероятности:
x(t)
t
t1
t2
x1 = x(t1) x2 = x(t2)
x x x x p( x , x ) d x d x
Rx (t1 , t2 ) x1 x1 x2 x2
1
1
2
2
1
2
1
2
Rx (t1 , t2 ) x1 x1 x2 x2 x1 x2 x1 x2 x1 x2 x1 x2
x1 x2 x1 x2 x1 x2 x1 x2 x1 x2 x1 x2
3.
Корреляционная функция стационарногослучайного процесса:
Для стационарного случайного процесса
= t2 t1
Rx (t1 , t2 ) Rx (t2 t1 ) Rx (τ) x x xτ x xxτ x
2
Свойства корреляционной функции стационарного СП
1. Rx(– ) = Rx( ).
2. Rx(0) = 2.
3. Rx( ) Rx(0).
Нормированная
корреляционная функция
r ( τ)
R( τ)
σ
2
4.
а)R1( )
x1(t)
10
20
30
40
t, мкс
б)
R2( )
x2 (t)
10
20
30
2
2
40
t, мкс
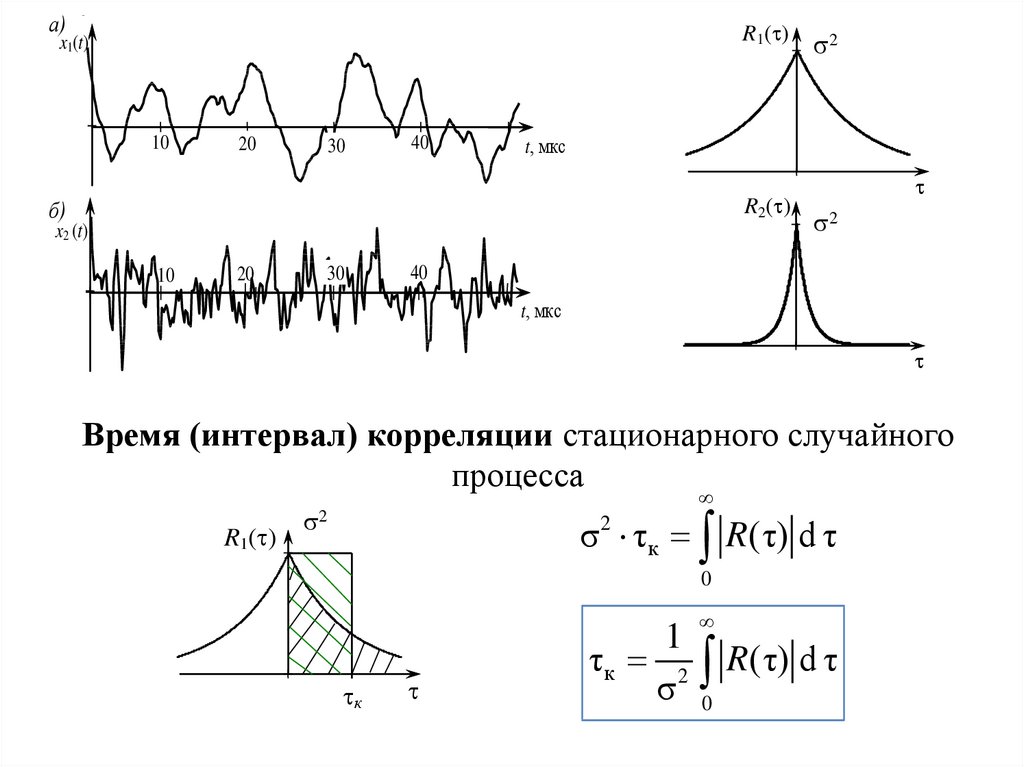
Время (интервал) корреляции стационарного случайного
процесса
R1( )
2
σ 2 τ к R(τ) d τ
0
к
1
τк 2
σ
R(τ) d τ
0
5.
Корреляционная функция гармонического сигналасо случайной равномерно распределенной фазой
1
p(φ)
2π
x(t ) A cos( ω0t )
при π φ π
Rx (t1 , t2 ) ( x1 x1 )( x2 x2 )
f (ξ)
f (ξ) p(ξ) d ξ
π
1
x A cos(ω0t φ) A cos(ω0t φ) d φ 0
2π
π
π
Rx (t1 , t2 ) x1 x2
A cos(ω t
0 1
π
φ) A cos(ω0t2 φ) p (φ) d φ
6.
Корреляционная функция гармонического сигналасо случайной равномерно распределенной фазой
π
A2
1
cos ω0 (t1 t2 ) 2 cos ω0 (t2 t1 ) d
Rx (t1, t2 )
2 π
2π
2 π
A
2
cos ω0 (t1 t2 ) 2
π
A2
cos ω0 (t2 t1 )
2
2 π
1
A
d
2π
2
cos ω0 (t2 t1)
π
t2 t1 τ
A2
Rx (τ)
cos(ω0 τ)
2
1
d
2π
7.
A2Rx (τ)
cos(ω0 τ)
2
R( )
А 2 / 2
T/2
x(t)
t2=t1+T/2
t
–A
= t2 t1
A
t1
T=2 / 0
t2=t1+T
8.
Взаимная корреляционная функцияХарактеризует корреляционную связь двух случайных процессов:
Rxy (t1, t2 ) ( x1 x1 )( y2 y2 )
( x1 x1)( y2 y2 ) p( x1, y2 )dx1dy2
x1 = x(t1), y2 = y(t2)
Cлучайные процессы x(t) и y(t) называют стационарно
связанными, если взаимно корреляционная функция зависит
только от разности
= t2 t1
9.
Если случайные процессы x(t) и y(t) независимы, товзаимно корреляционная функция равна нулю при любых
значениях аргументов
Rxy (t1 , t2 )
( x x )( y
1
1
2
y2 ) p1 ( x1 ) p2 ( y2 )dx1dy2
( x x ) p ( x )dx ( y
1
1
1
1
1
2
y2 ) p2 ( y2 )dy2
x1 p1 ( x1 )dx1 x1 p1 ( x1 )dx1 y2 p2 ( y2 )dy2 y2 p2 ( y2 )dy2
x1 x1
y
2
y2 0
10.
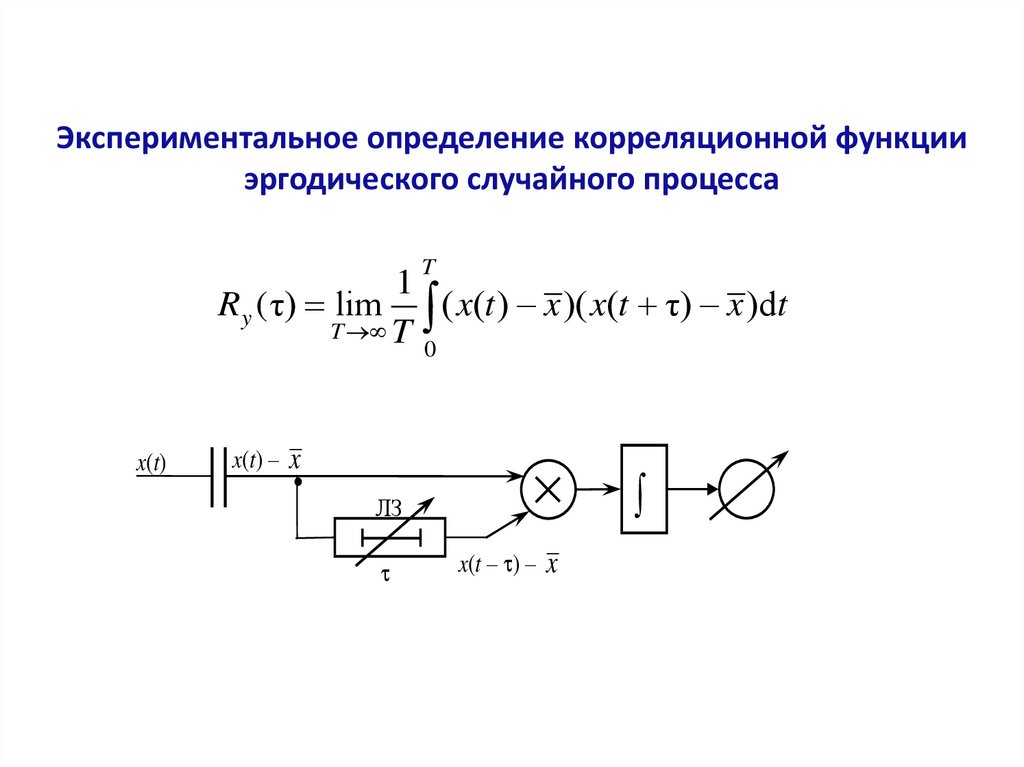
Экспериментальное определение корреляционной функцииэргодического случайного процесса
T
1
Ry (τ) lim ( x(t ) x )( x(t τ) x )dt
T T
0
x(t)
x(t) –
x
.
ЛЗ
x(t – ) –
x
11.
Спектральная плотность мощности(спектр мощности, энергетический спектр)
эргодического случайного процесса с x 0
T
S (ω) x (t ) e
(i )
T
(i )
T
jωt
*
(i )
T
WT (ω) ST(i ) (ω) S (ω)
dt
0
T
2
1
(i )
(i )
ET xT (t2 ) d t
ST (ω) d t
2π
0
Энергия реализации
2
Средняя мощность реализации
2
ET
1 WT (ω)
xT(i ) (t )
dω
T
2π T
Совершим предельный переход T (проведем усреднение по реализациям)
x(t )
2
1
WT (ω)
σ2
lim
dω
T
2π
T
Спектральная плотность мощности
случайного процесса
WT (ω)
W (ω) lim
T
T
12.
Свойства энергетического спектра1. W( ) 0
2. Теорема Винера - Хинчина
W (ω)
jωτ
R
(
τ
)
e
dτ
x
1
jωτ
Rx (τ)
W
(ω)e
dω
2π
3. W(– ) = W( )
W (ω)
R (τ ) cos(ωτ) j sin(ωτ) d τ R ( τ ) cos(ωτ) d τ
x
x
4. Связь СПМ и дисперсии случайного процесса
1
1
σ 2 Rx (0)
W (ω)d ω W (ω)d ω
2π
π0
13.
Односторонний спектр мощности (энергетический спектр)1
W (ω), ω 0
F (ω) π
0,
ω 0
2
F (ω) Rx ( τ) cos(ωτ) d τ
π0
Rx ( τ) F (ω) cos(ωτ) d ω
0
σ 2 F (ω) d ω
0
Эффективная ширина спектра
F (ω)
1
ωэф
F (ω) d ω
Fmax 0
Fmax
ω
ωэф
π
ωэф τ к
2
14.
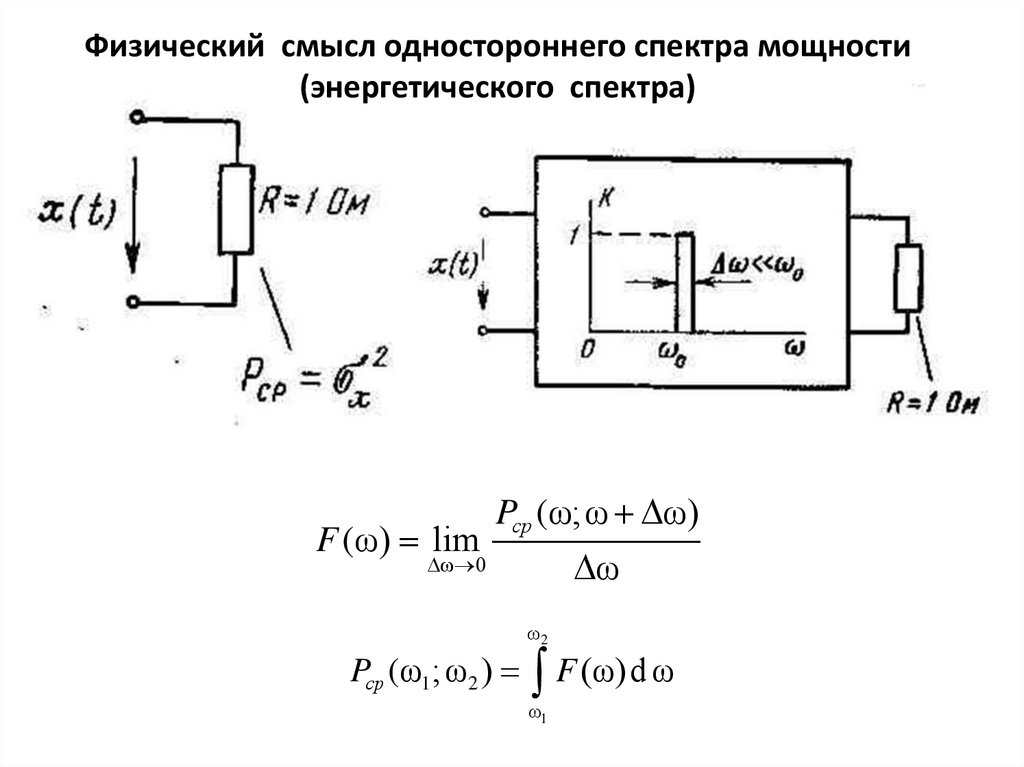
Физический смысл одностороннего спектра мощности(энергетического спектра)
F (ω) lim
Pср (ω;ω ω)
ω
ω 0
Pср (ω1 ;ω2 )
ω2
F (ω) d ω
ω1
15.
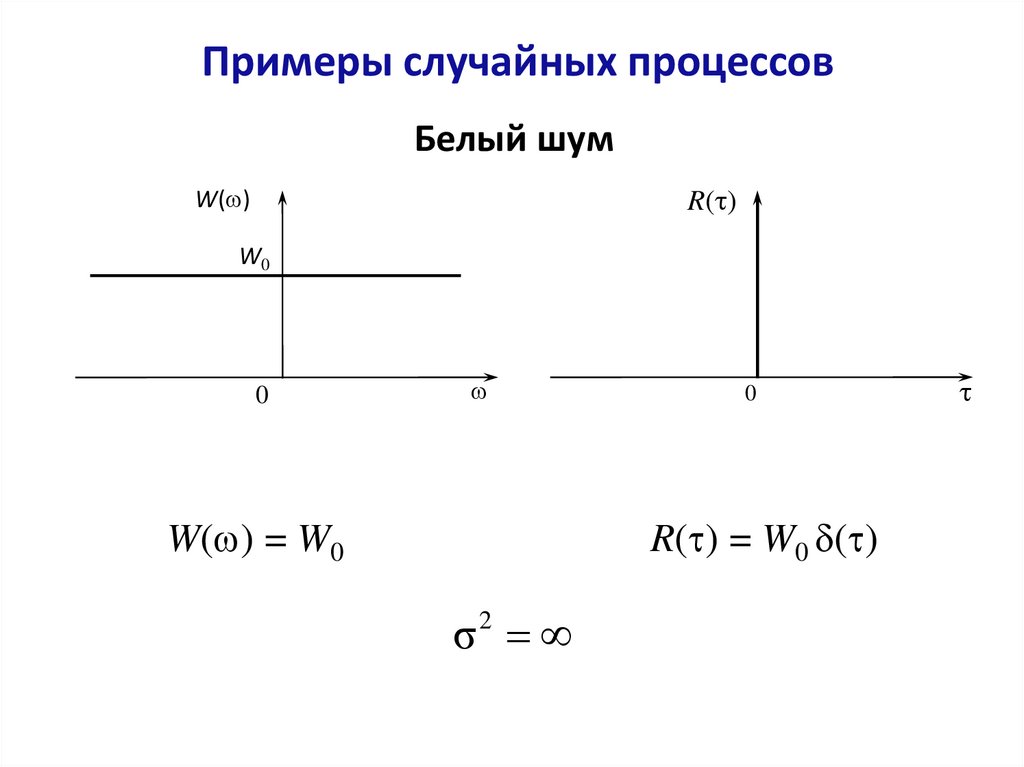
Примеры случайных процессовБелый шум
W( )
R( )
W0
0
0
R( ) = W0 ( )
W( ) = W0
σ2
16.
Белый шум с ограниченным спектромW( )
1
R(τ)
2
W0
– в
W0 e jωτ d ω
ωв
W0 (e jωв τ e jωв τ ) W0 sin(ωв τ)
2 jτ
πτ
в
0
ωв
W0ωв sin( ωв τ)
R ( τ)
π
ωв τ
R( )
2
W0 ωв
σ
F0 ωв
π
2
0
/ в
2 / в
17.
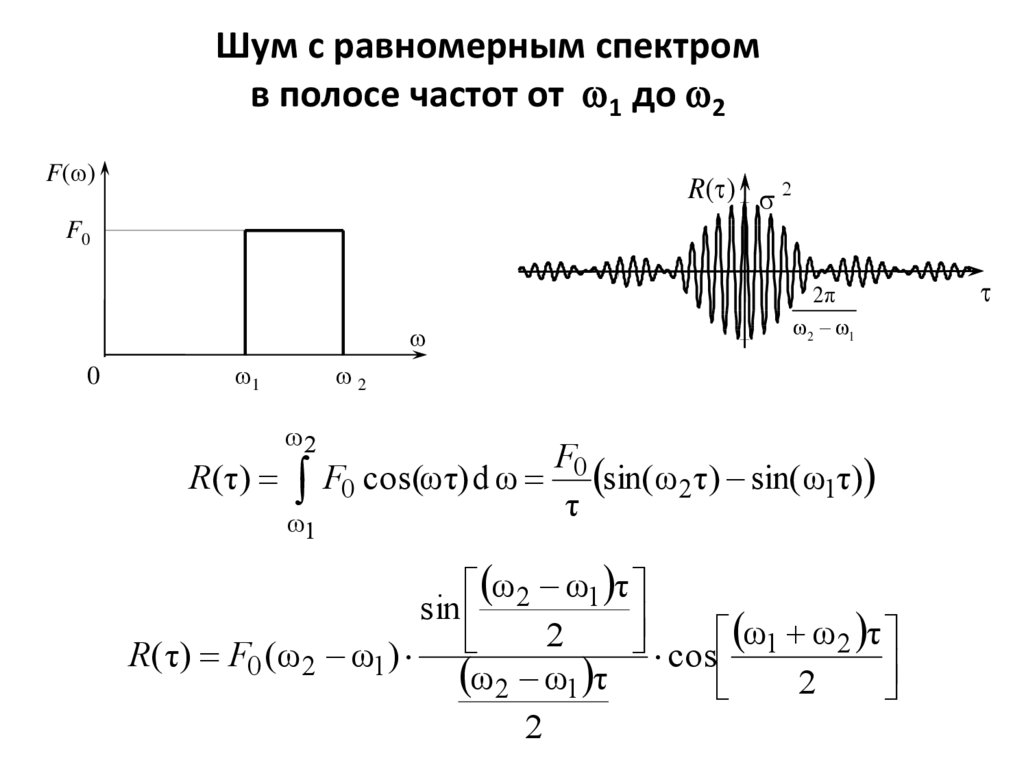
Шум с равномерным спектромв полосе частот от 1 до 2
F( )
R( )
F0
0
1
R( τ)
2π
ω2 ω1
2
ω2
ω1
F0 cos(ωτ) d ω
F0
sin( ω2 τ) sin( ω1τ)
τ
ω2 ω1 τ
sin
2
ω ω2 τ
R( τ) F0 (ω2 ω1 )
cos 1
ω2 ω1 τ
2
2
18.
Источники шумов в радиотехнических устройствахТепловой шум
2
формула Найквиста
F (ω) kTR
π
k = 1,38 10 –23 Дж/град — постоянная Больцмана,
Т — абсолютная температура, в градусах Кельвина,
R — сопротивление проводника, Ом.
Дисперсия в полосе частот
2
σ kTR Δω 4kTR Δf
π
2
Пример: дисперсия теплового шума, создаваемого резистором
R = 1 кОм в полосе частот f = 1 МГц при комнатной температуре:
σ 2 4 1,38 10 23 293 103 106 1, 6 10 11
Uэфф = = 4 10 –6 В = 4 мкВ.
В2
19.
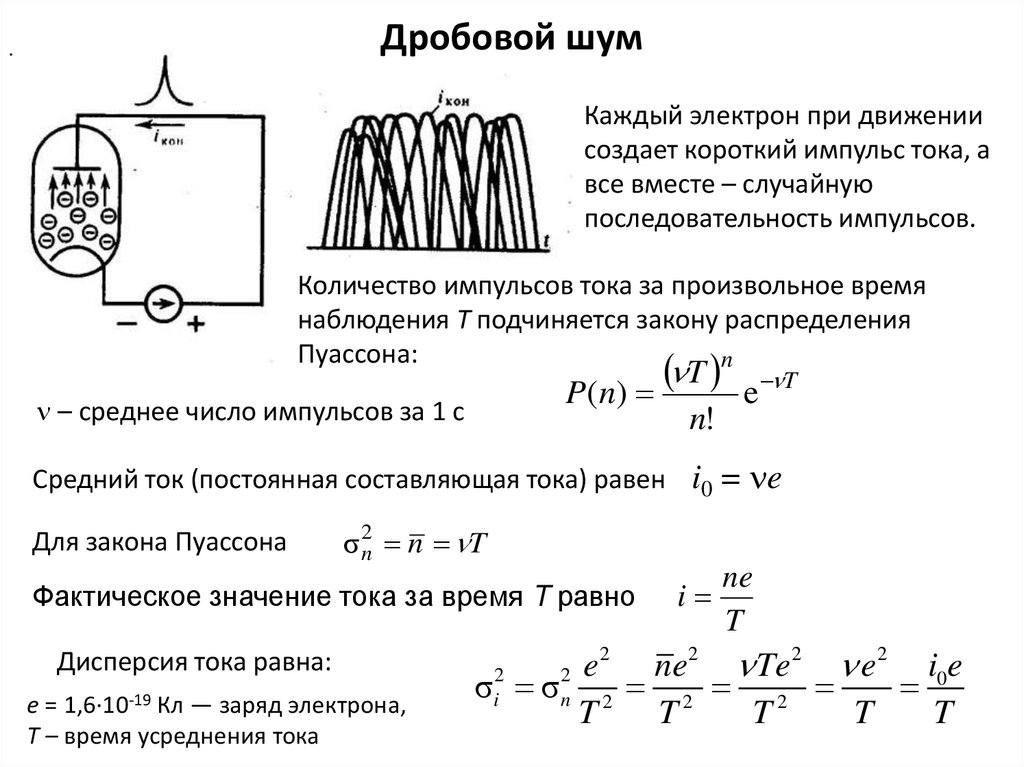
Дробовой шум.
Каждый электрон при движении
создает короткий импульс тока, а
все вместе – случайную
последовательность импульсов.
Количество импульсов тока за произвольное время
наблюдения T подчиняется закону распределения
Пуассона:
n
P ( n)
– среднее число импульсов за 1 с
T
n!
e T
Средний ток (постоянная составляющая тока) равен i0 = e
Для закона Пуассона
σ 2n n T
Фактическое значение тока за время T равно
Дисперсия тока равна:
e = 1,6·10-19 Кл — заряд электрона,
Т – время усреднения тока
i
ne
T
2
2
2
2
e
ne
Te
e
i0e
2
2
σi σ n 2 2 2
T
T
T
T
T
20.
Спектр мощности дробового шумаПредположим для определенности, что импульс тока, создаваемый одним
пролетающим электроном, имеет прямоугольную форму
ωTи
sin
2
2
Энергетический спектр одного импульса
S e (ω) e 2
ωTи
2
2
2
ωTи
ωTи
sin
sin
2
2
W (ω) e 2
i0 e
ωTи
ωTи
2
2
2
W( )
i0 e
Ти ~ 10–9 с
2 /Tи
i0e
формула Шотки
F (ω)
π
21.
Пример: дисперсия дробового шума диода в режименасыщения при токе i0 = 100 мА и полосе частот 1 МГц:
19
i
e
0
,
1
1
,
6
10
i2 0 ω
2π 10 6 3,2 10 14 A2 ,
π
π
Эффективное значение шумового тока i = 1,79 10–7 0,18 мкА.
При сопротивлении нагрузки 1 кОм эффективное значение
напряжения будет равным Uэфф = 1,79 10–4 В = 179 мкВ
22.
В транзисторах существует несколько источников шума.Основными из них являются следующие:
• тепловой шум сопротивления базы, как электрода с самым
большим сопротивлением;
• дробовой шум эмиттерного перехода;
• дробовой шум коллекторного перехода;
• шум токораспределения: носители, прошедшие через
эмиттерный переход, могут попадать как на коллектор, так и
на базу (этот процесс является случайным и вносит свой
вклад в шум транзистора);
• шум 1/f , или фликкер-эффект. Спектр мощности этого шума
зависит от частоты как 1/f и поэтому он проявляется на
самых низких частотах.















 physics
physics








