Основы теории случайных процессов. Часть 2

1. Основы теории СЛУЧАЙНЫХ ПРОЦЕССОВ - 2

Кафедра «КРЭМС»
Основы теории
СЛУЧАЙНЫХ
ПРОЦЕССОВ - 2
Зырянов
Юрий Трифонович
доктор технических наук
профессор

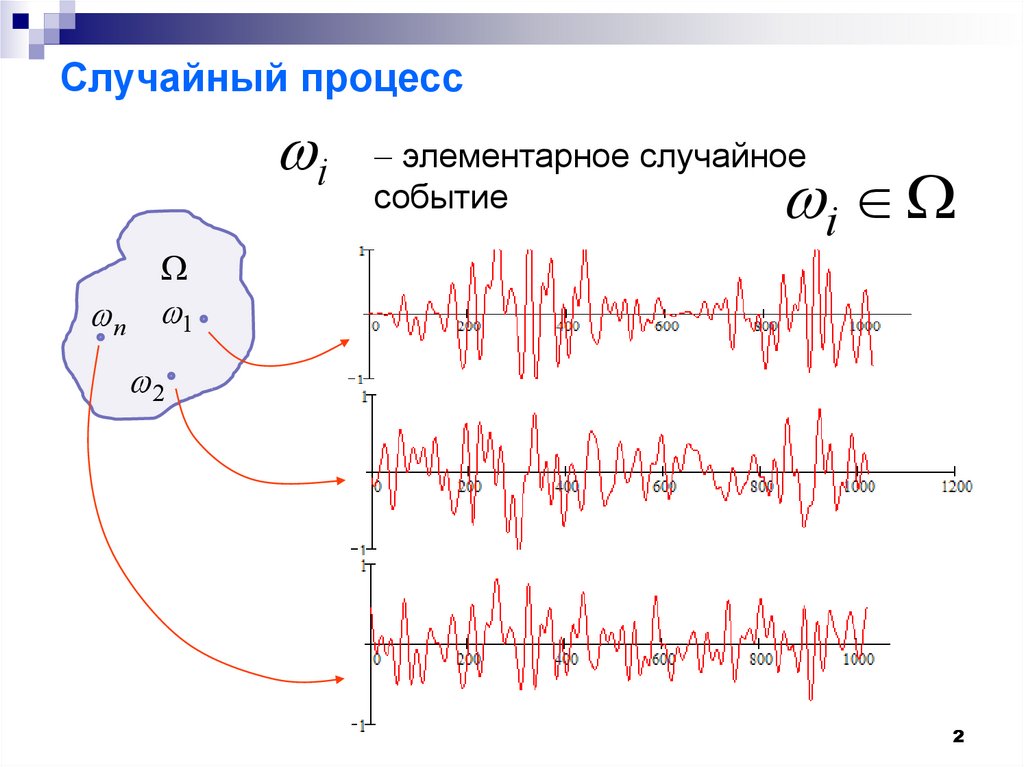
2. Случайный процесс

i
элементарное случайное
событие
i
n 1
2
2

3. Случайные процессы

Перейти от описания с.в. к описанию с.п. можно, рассматривая
совместные распределения двух, трех и т.д. значений x(t1 ),..., x(tn )
процесса в некоторые различные моменты времени
P 1 x1,..., n xn F ( x1,..., xn )
x1
xn
t t1,..., tn
... w( x1,..., xn )dx1...dxn
Зависимость от времени явно не указана для упрощения записи
... w( x1,..., xn )dx1...dxn 1 условие нормировки
n
Случайный процесс считается полностью определенным, если для любого
можно записать его совместную ПРВ при любом выборе моментов времени
3

4. Числовые характеристики СП

mk1...kn ...
kn
k1
x1 ...xn w( x1,..., xn )dx1...dxn
смешанные начальные моменты
M k1...kn ... ( x1 mx1)k1 ...( xn mxn )kn w( x1,..., xn )dx1...dxn
В частности, при
смешанные центральные моменты
k1 1 , k2 ... kn 0
получается математическое ожидание в сечении
При
t1
k2 2 , k1 k3 ... kn 0 дисперсия в сечении t 2
и т.д.
4

5. Моментные функции

В общем случае моменты совместной ПРВ зависят от
расположения сечений на оси времени и называются
моментными функциями.
Чаще всего используют второй смешанный
центральный момент
M11 Rx (t1, t2 )
( x1 mx1)( x2 mx2 )w( x1, x2 )dx1.dx2
( x1 mx1)( x2 mx 2 )
функция автокорреляции, или
автокорреляционная функция (АКФ)
здесь и далее явно не указана зависимость от времени, в
частности, функциями времени являются mx1 mx1 (t1 ) и
mx 2 mx 2 (t2 )
5

6. Совместное описание двух СП

x(t )
y (t )
n
Полное описание такой пары совместная ПРВ
1
отсчетов первого СП и
2 отсчетов второго процесса
при любых 1 и 2
n
n
n
Числовые характеристики всевозможные смешанные
моменты, наиболее широко используется
Rxy (t1, t2 )
( x1 mx1)( y2 my 2 )w( x1, y2 )dx1.dy2
( x1 mx1)( y2 m y 2 ) взаимно корреляционная
функция
6

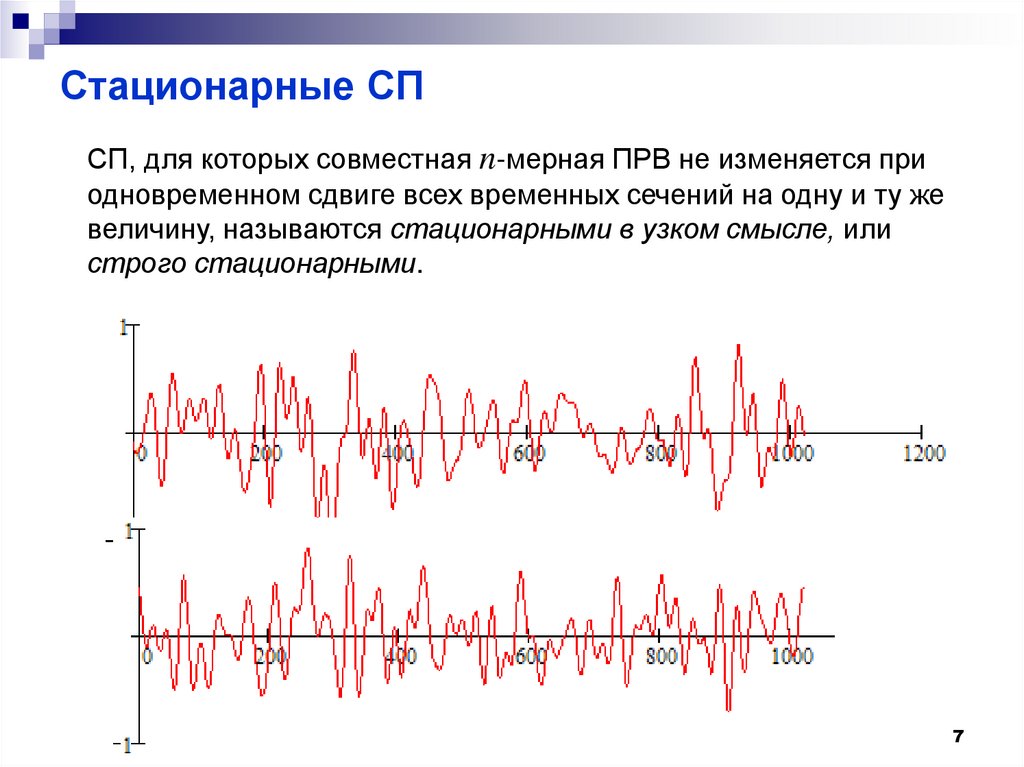
7. Стационарные СП

СП, для которых совместная n-мерная ПРВ не изменяется при
одновременном сдвиге всех временных сечений на одну и ту же
величину, называются стационарными в узком смысле, или
строго стационарными.
7

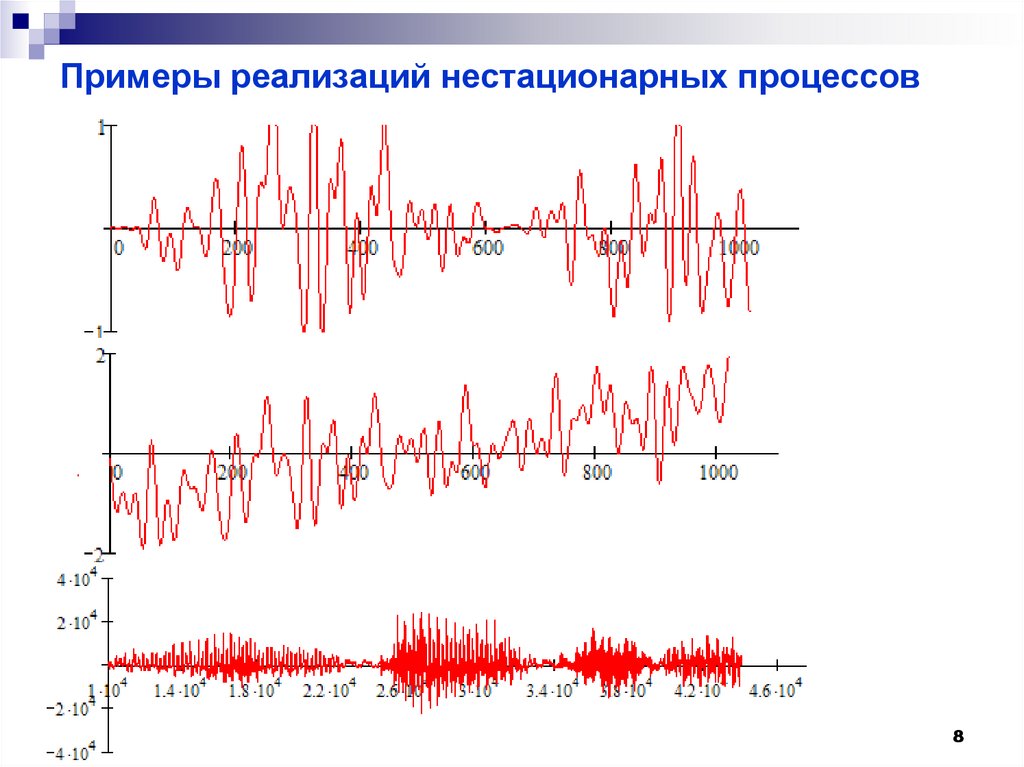
8. Примеры реализаций нестационарных процессов

8

9. Стационарные в широком смысле СП

СП называется стационарным в широком смысле,
если при одновременном сдвиге сечений не
изменяются лишь его моменты не выше второго
порядка.
mx (t ) mx
Rx (t1, t2 ) Rx (t2 t1) Rx ( )
Заметим, что
Rx (0) Dx
(второй центральный момент)
откуда следует постоянство
дисперсии
СП, стационарный в узком смысле, стационарен и в широком смысле.
Обратное в общем случае неверно!
9

10. Обратный пример (частный случай)

w( x1, x2 ,...., xn )
1
(2 )
r
n /2
1 2 .... n r
1/2
e
( xi mi ) ( x j m j )
1 n n
Aij
2 r i 1 j 1
i
j
определитель квадратной матрицы, составленной из
попарных коэффициентов корреляции отсчетов
A ij алгебраическое дополнение элемента rij
10

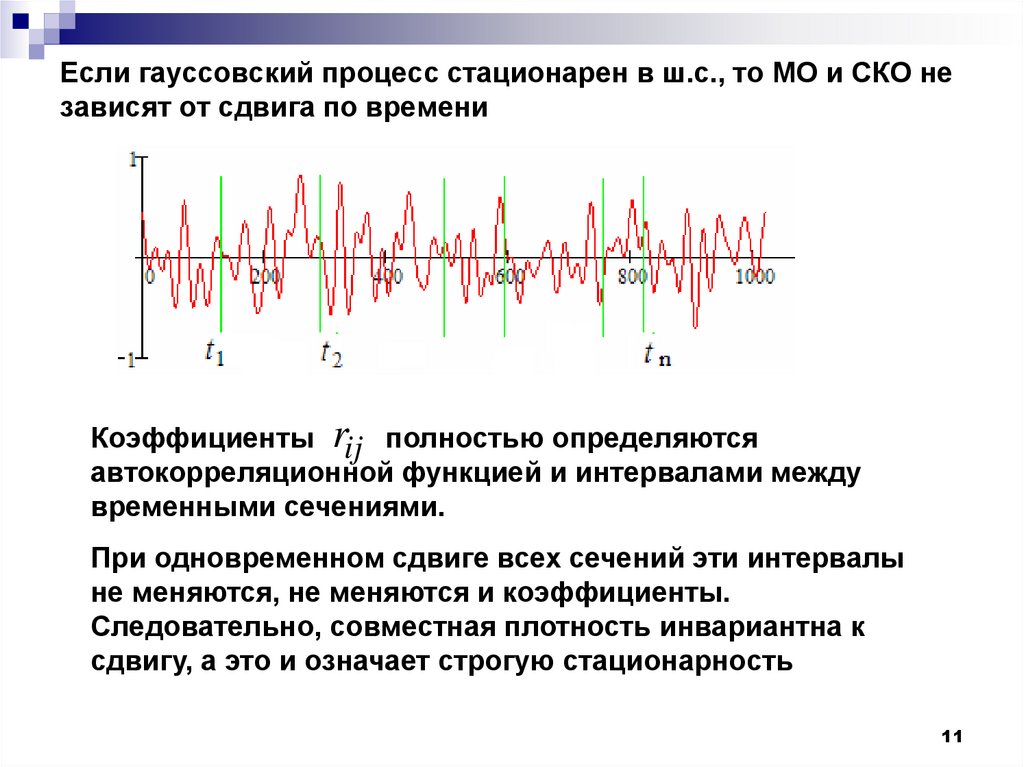
11. Если гауссовский процесс стационарен в ш.с., то МО и СКО не зависят от сдвига по времени

Коэффициенты rij полностью определяются
автокорреляционной функцией и интервалами между
временными сечениями.
При одновременном сдвиге всех сечений эти интервалы
не меняются, не меняются и коэффициенты.
Следовательно, совместная плотность инвариантна к
сдвигу, а это и означает строгую стационарность
11

12. Эргодические случайные процессы

Для эргодических процессов моменты, найденные
усреднением по ансамблю, равны соответствующим
моментам, найденным усреднением по времени
T
1
k
lim x(t ) dt
T T
mk x(t )
k
0
M k x(t ) m
k
T
1
k
lim x(t ) m dt
T T
0
В частности
T
1
m x(t ) lim x(t )dt
T T
0
D x(t ) m
2
T
1
2
lim x(t ) m dt
T T
0
12

13. АКФ

R( ) x(t ) m x(t ) m x(t ) x(t ) m 2
T
1
lim x(t ) x(t )dt m 2 .
T T
0
Обычно наблюдателю доступна лишь одна (хотя, возможно,
достаточно длинная) реализация случайного процесса.
Эргодичность означает, по существу, то, что эта единственная
реализация является полноправным представителем всего
ансамбля
Достаточные условия эргодичности стационарного СП
T
lim R( ) 0
1
lim R( )d 0
T T
0
13

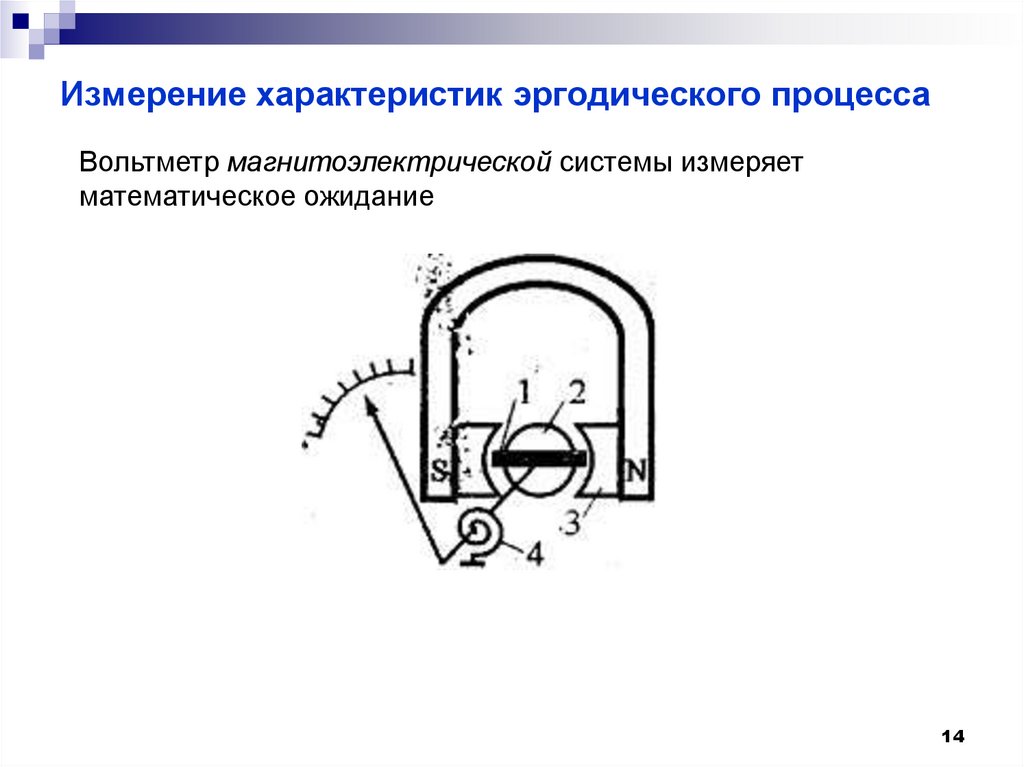
14. Измерение характеристик эргодического процесса

Вольтметр магнитоэлектрической системы измеряет
математическое ожидание
14

15. Измерение характеристик эргодического процесса

Вольтметр электромагнитной или термоэлектрической системы,
подключенный через разделительную емкость (для исключения
постоянной составляющей) – измеряет среднеквадратическое
значение (СКО)
15

16. Измерение характеристик эргодического процесса

Прибор для измерения АКФ (коррелометр)
16