Основы теории случайных процессов

1. Основы теории СЛУЧАЙНЫХ ПРОЦЕССОВ

Кафедра «КРЭМС»
Основы теории
СЛУЧАЙНЫХ
ПРОЦЕССОВ
Зырянов
Юрий Трифонович
доктор технических наук
профессор

2. Основные понятия теории вероятностей

Все сигналы и все помехи являются случайными, то
есть непредсказуемыми.
Математическими моделями случайных сигналов и
помех служат случайные процессы.
В основе лежит понятие случайного события
Пространство элементарных
событий (генеральная
совокупность)
элементарное событие
A случайное событие
A
2

3. Основные понятия теории вероятностей

A
A случайное событие
A
элементарное случайное
событие
P
вероятностная мера (функция
множеств)
P : 2 0;1
P A вероятность случайного
события
P 1
A
достоверное событие
3

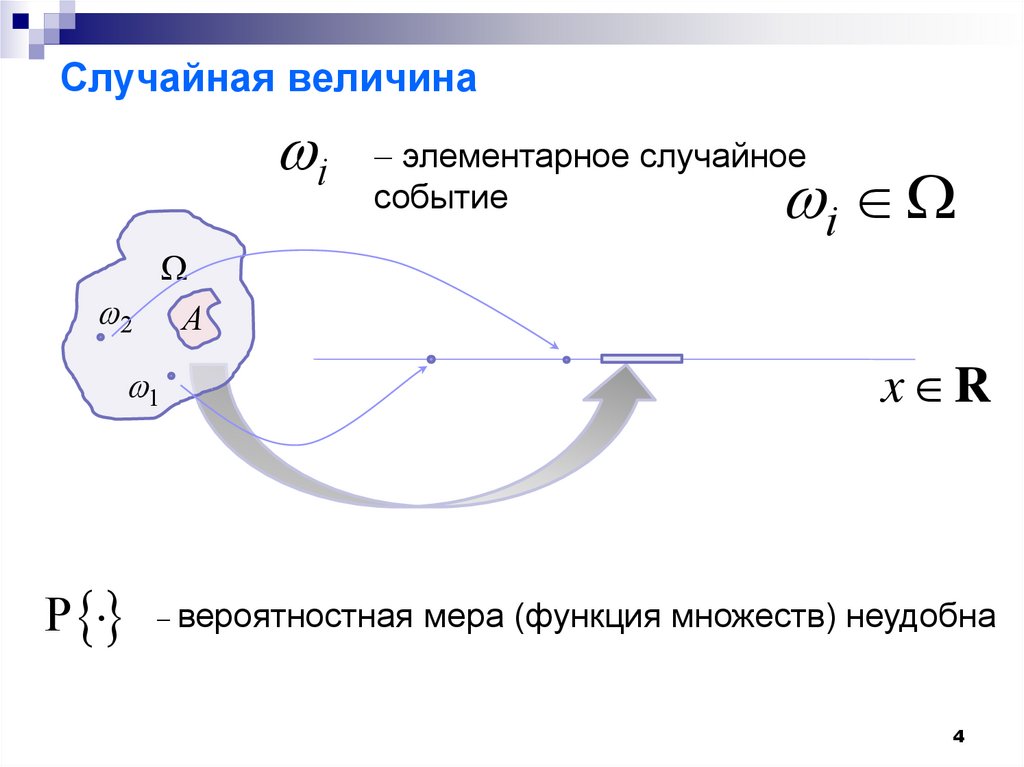
4. Случайная величина

i
2
1
элементарное случайное
событие
i
A
x R
P
вероятностная мера (функция множеств) неудобна
4

5. Случайная величина

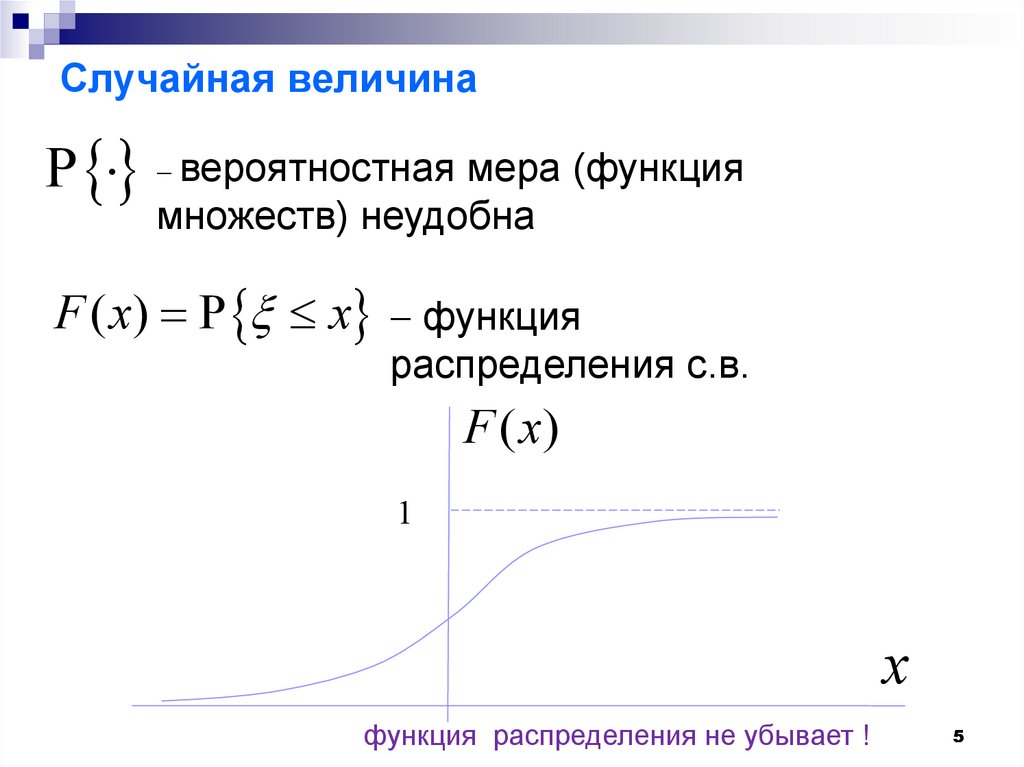
P
вероятностная мера (функция
множеств) неудобна
F ( x) P x функция
распределения с.в.
F ( x)
1
x
функция распределения не убывает !
5

6.

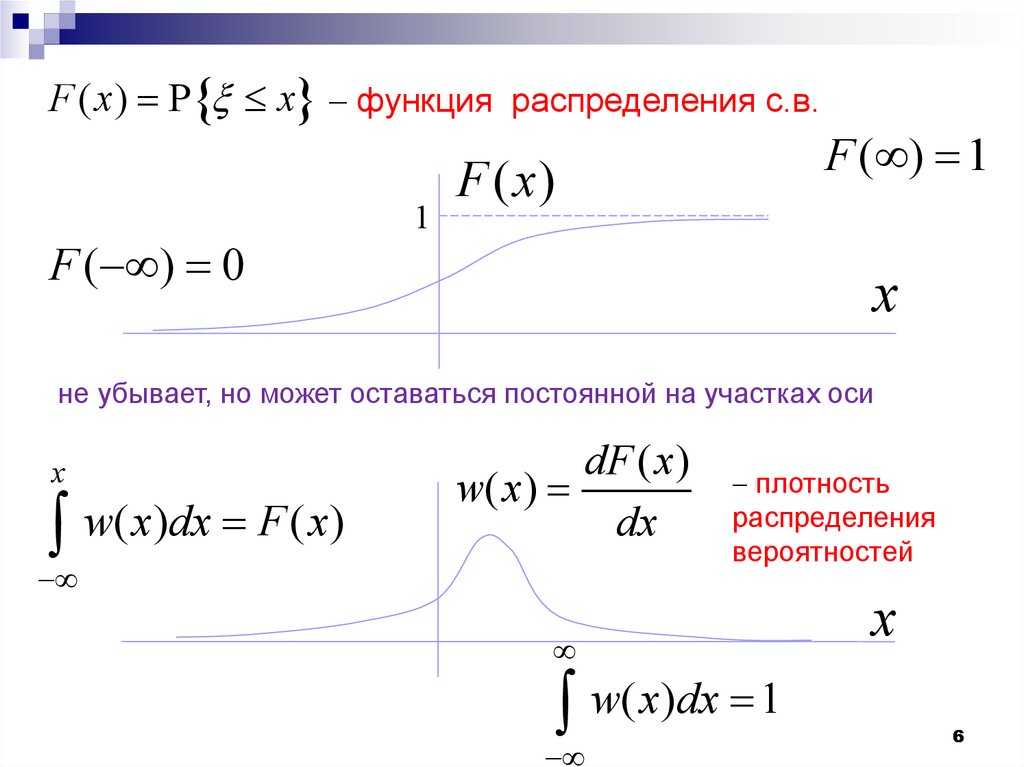
F ( x) P x функция распределения с.в.
F ( ) 0
1
F ( x)
F ( ) 1
x
не убывает, но может оставаться постоянной на участках оси
x
w( x)dx F ( x)
dF ( x)
w( x)
dx
плотность
распределения
вероятностей
w( x)dx 1
x
6

7.

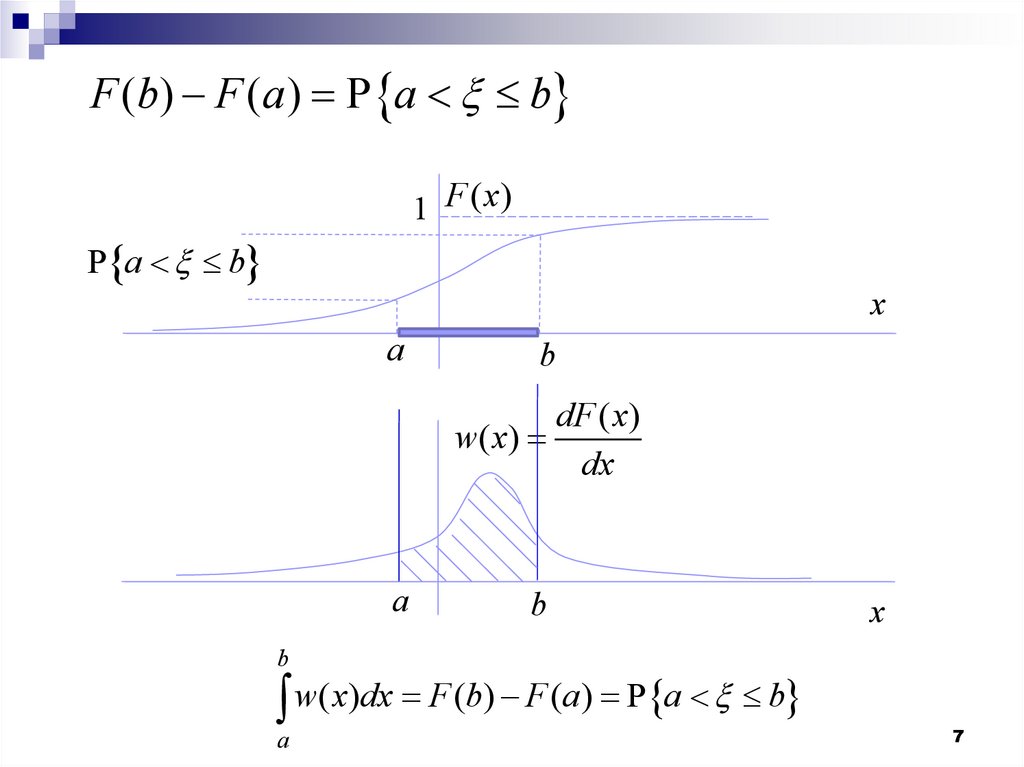
F (b) F (a ) P a b
1 F ( x)
P a b
x
a
b
w( x)
a
dF ( x)
dx
b
x
b
w( x)dx F (b) F (a) P a b
a
7

8. Примеры ФР и ПРВ

F ( x)
a
1 F ( x)
b
F ( x) 1 e ax , x 0
x
x
w( x)
w( x)
a
1
b a
a
b x
равномерное распределение
w( x) ae ax , x 0
x
экспоненциальное распределение
8

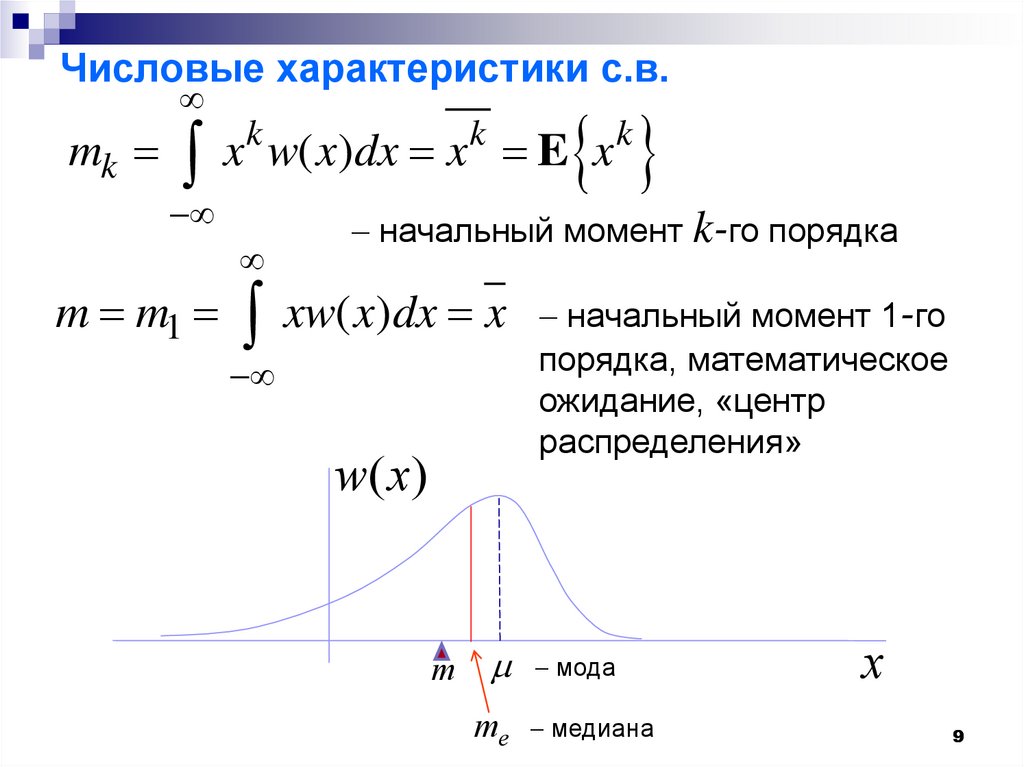
9. Числовые характеристики с.в.

mk x w( x)dx x E x
k
k
k
начальный момент k-го порядка
m m1 xw( x)dx x начальный момент 1-го
порядка, математическое
ожидание, «центр
распределения»
w( x)
m
мода
me медиана
x
9

10.

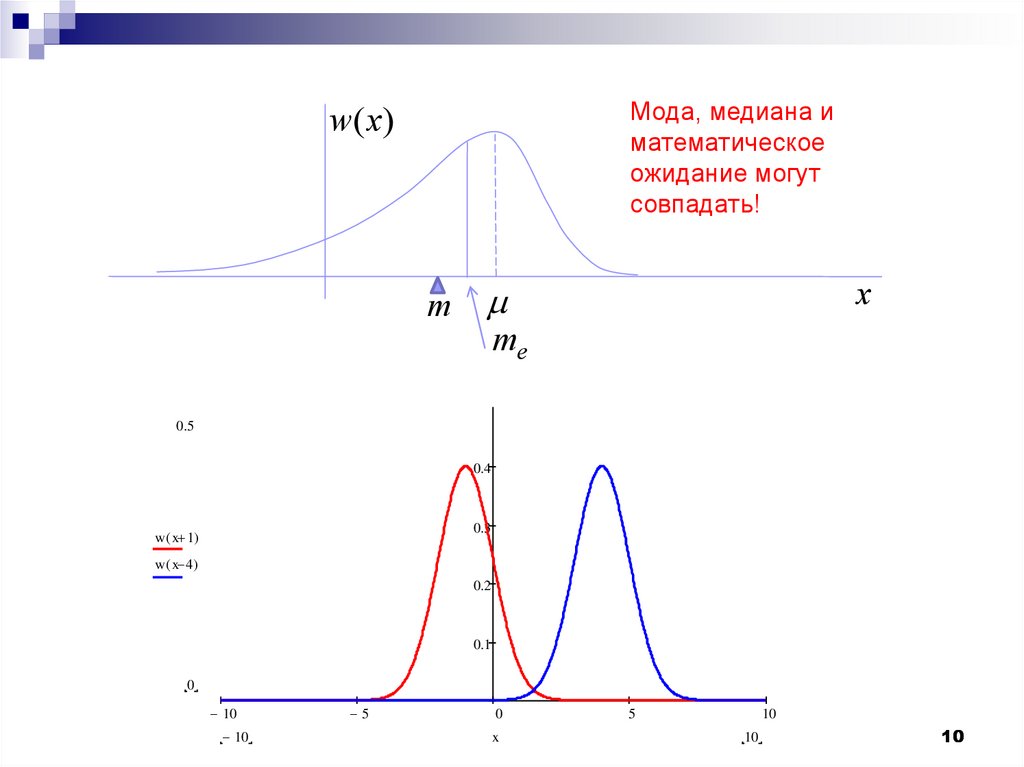
Мода, медиана и
математическое
ожидание могут
совпадать!
w( x)
m
x
me
0.5
0.4
0.3
w ( x 1)
w ( x 4)
0.2
0.1
0
10
10
5
0
x
5
10
10
10

11.

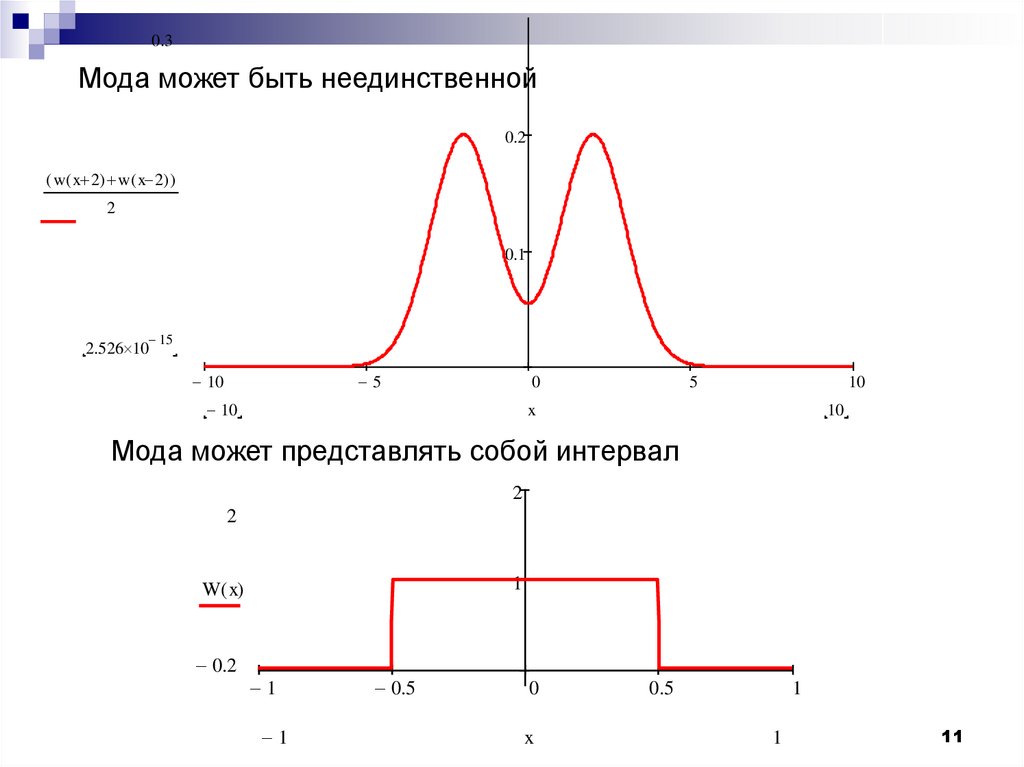
0.3
Мода может быть неединственной
0.2
( w ( x 2) w ( x 2) )
2
0.1
2.526 10
15
10
5
0
10
5
10
x
10
Мода может представлять собой интервал
2
2
1
W( x)
0.2
1
1
0.5
0
x
0.5
1
1
11

12.

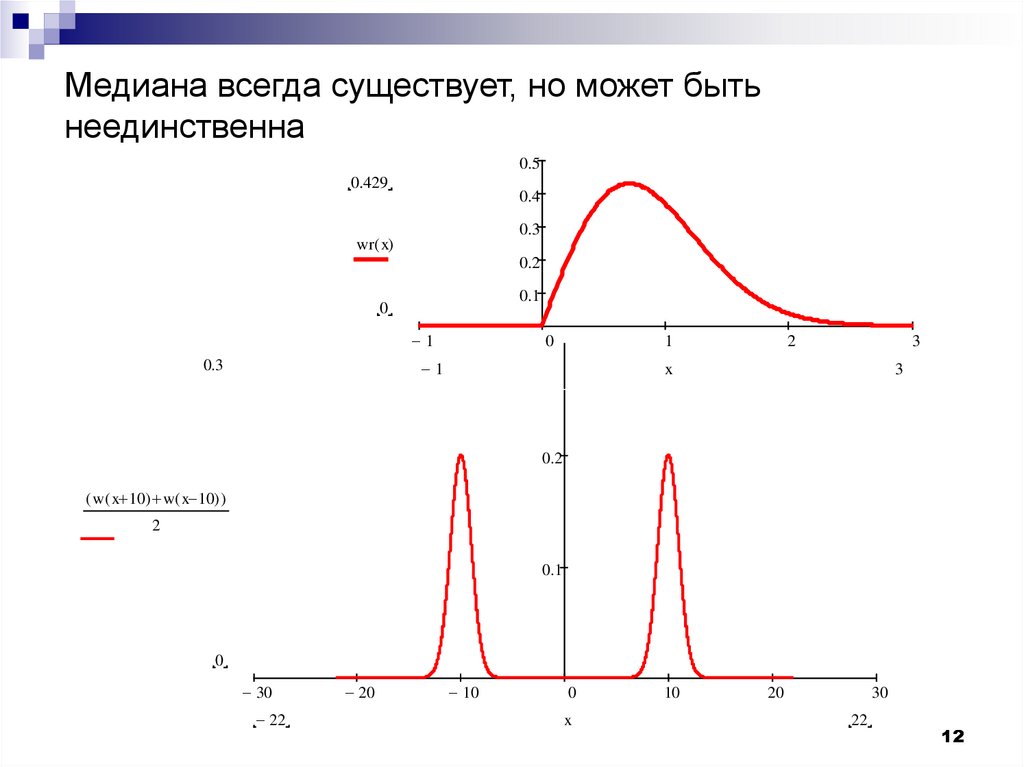
Медиана всегда существует, но может быть
неединственна
0.5
0.429
0.4
0.3
wr( x)
0.2
0.1
0
1
0
1
1
0.3
2
3
x
3
0.2
( w ( x 10) w ( x 10) )
2
0.1
0
30
22
20
10
0
x
10
20
30
22
12

13.

Математическое ожидание (и другие моменты)
существуют не всегда
(пример – распределение Коши)
w( x)
1
b x a / b 1
2
0.4
0.318
0.3
w . ( x)
0.2
0.1
6.563 10
4
10
10
5
0
x
5
10
10
13

14.

M k ( x m)k w( x)dx ( x m)k E ( x m)k
центральный момент k-го порядка
D M 2 ( x m) w( x)dx ( x m) E ( x m)
2
2
2
центральный момент 2-го порядка (дисперсия)
D среднеквадратическое отклонение (СКО)
14

15.

D M 2 ( x m) w( x)dx ( x m) E ( x m)
2
D
2
2
центральный момент 2-го порядка (дисперсия)
среднеквадратическое отклонение (СКО)
m2 x w( x)dx x E x
2
2
2
средний квадрат
D ( x m) w( x)dx ( x 2mx m ) w( x)dx
2
2
2
m2 2m m
2
2
m2 m
2
15

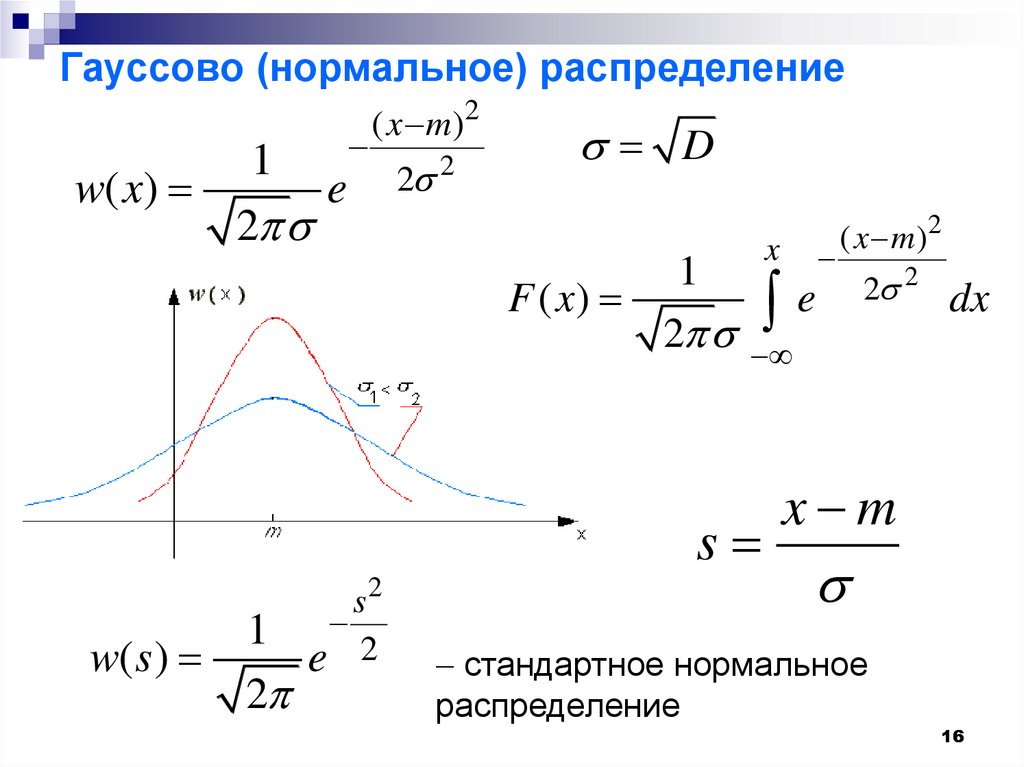
16. Гауссово (нормальное) распределение

( x m)2
1
2
2
w( x)
e
2
D
1
2
2
F ( x)
e
dx
2
x
s
1
w( s )
2
s2
e 2
( x m)2
x m
стандартное нормальное
распределение
16

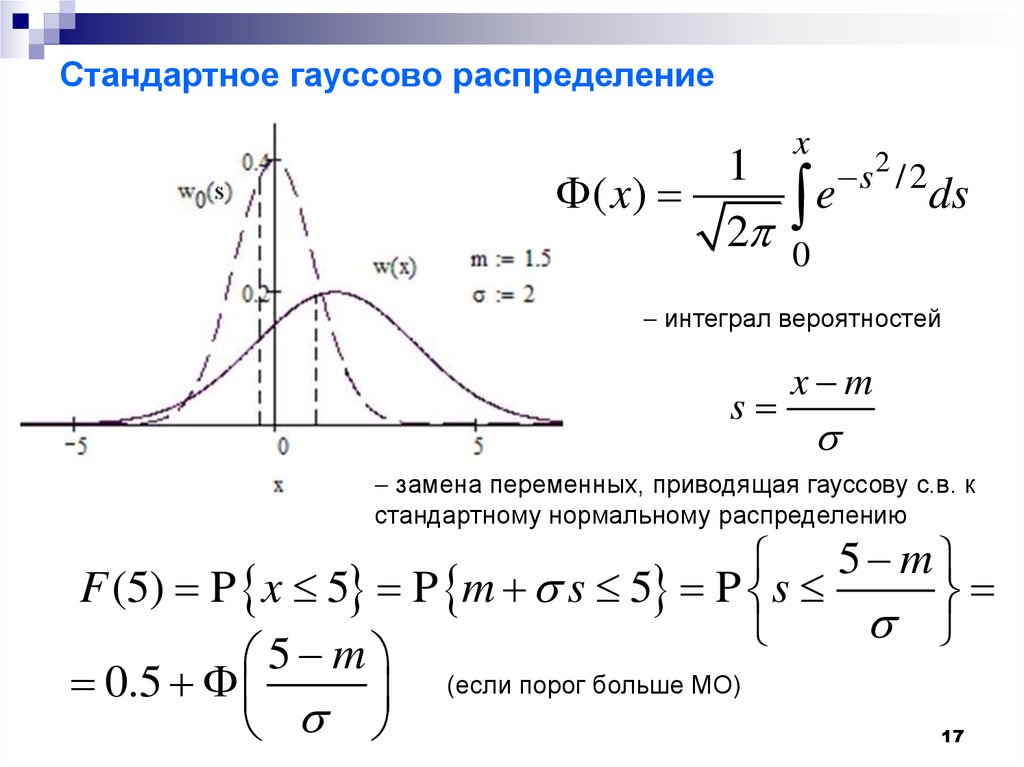
17. Стандартное гауссово распределение

x
1
s 2 /2
( x)
e
ds
2 0
интеграл вероятностей
s
x m
замена переменных, приводящая гауссову с.в. к
стандартному нормальному распределению
5 m
F (5) P x 5 P m s 5 P s
5 m (если порог больше МО)
0.5
17

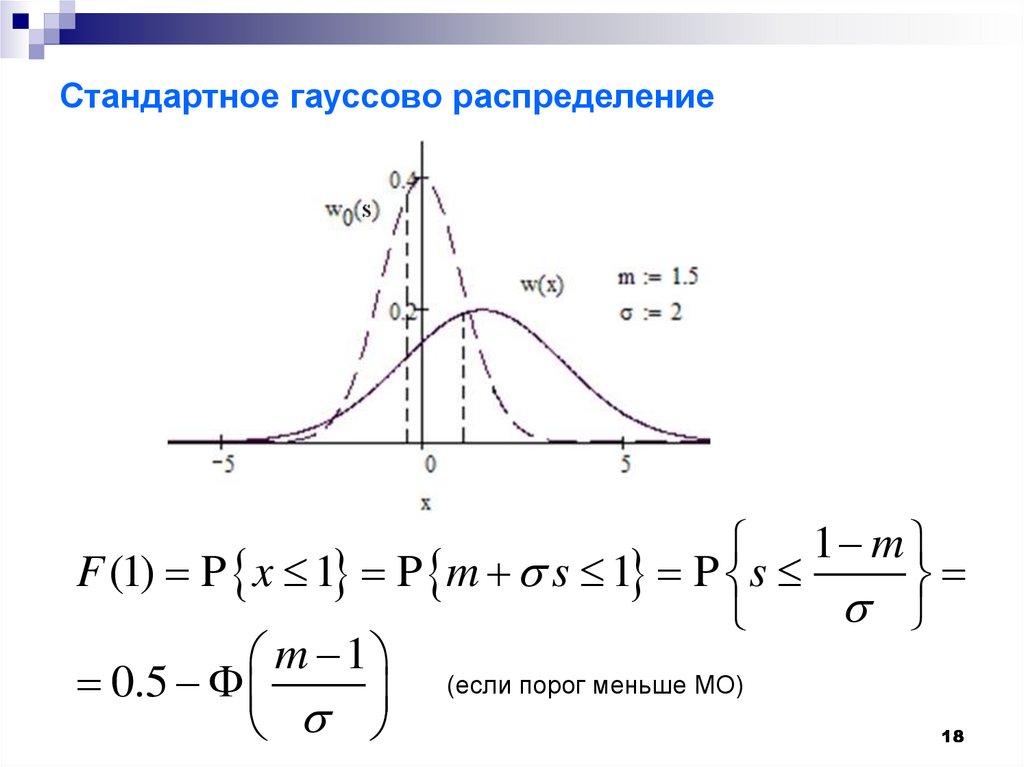
18. Стандартное гауссово распределение

1 m
F (1) P x 1 P m s 1 P s
m 1 (если порог меньше МО)
0.5
18

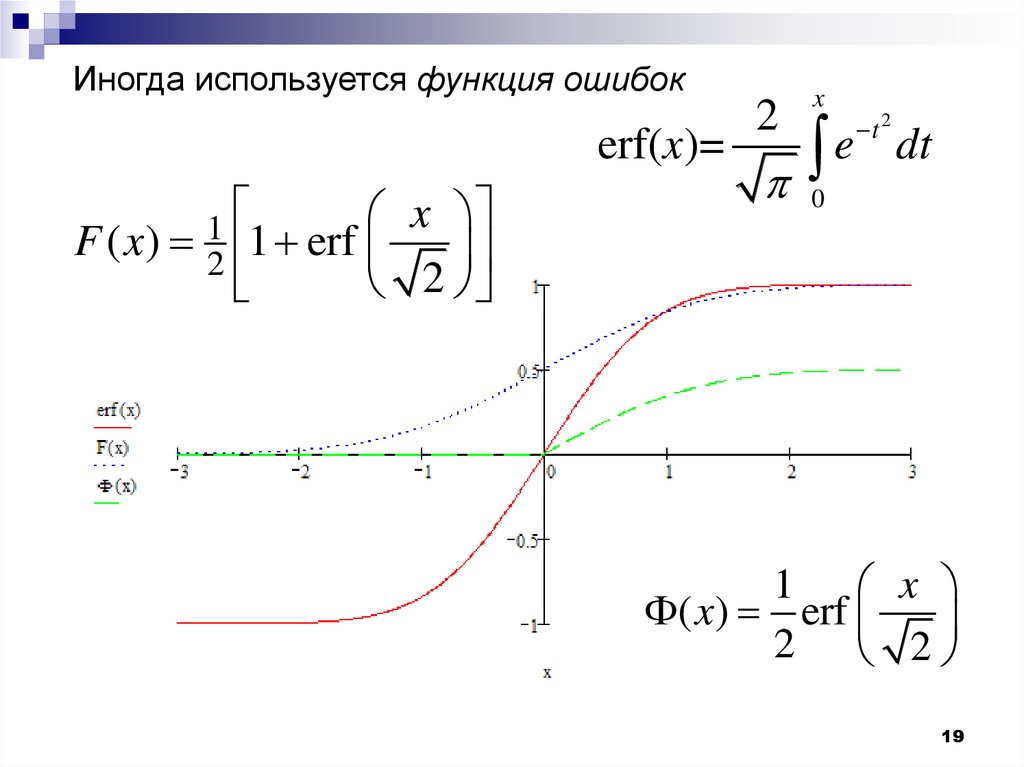
19.

Иногда используется функция ошибок
erf(x)=
x
1
F ( x) 2 1 erf
2
2
x
e dt
t 2
0
1 x
( x) erf
2 2
19

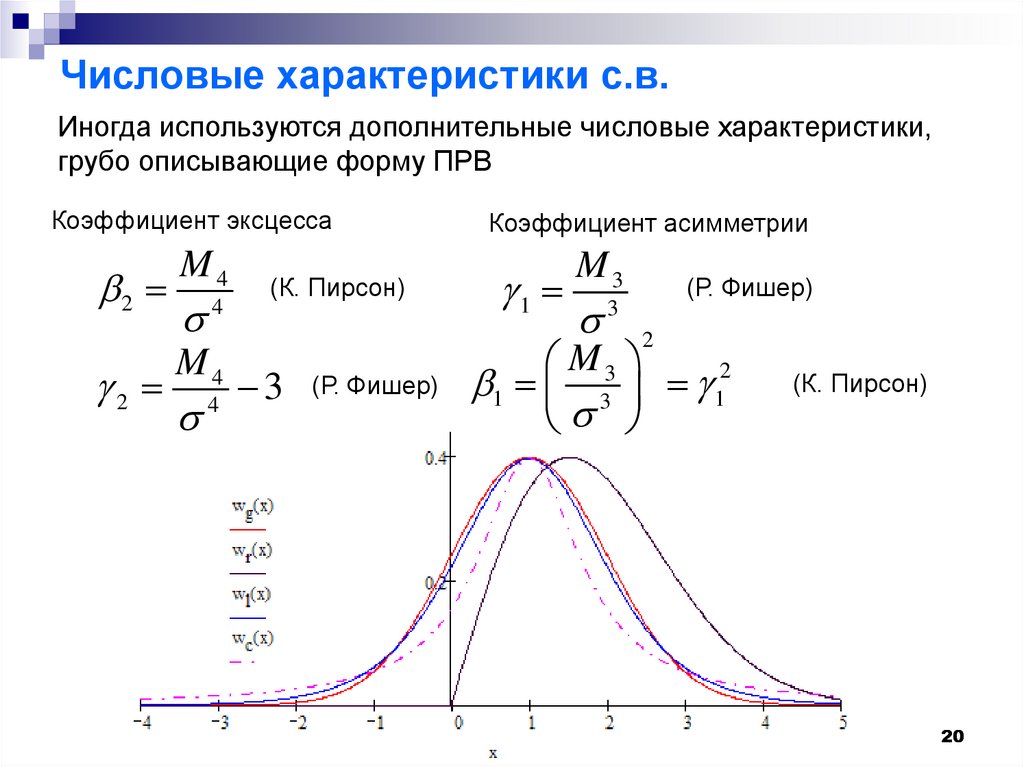
20. Числовые характеристики с.в.

Иногда используются дополнительные числовые характеристики,
грубо описывающие форму ПРВ
Коэффициент эксцесса
2
M4
2
M4
4
(К. Пирсон)
3
4
(Р. Фишер)
Коэффициент асимметрии
1
M3
(Р. Фишер)
2
M3
1 3 12
3
(К. Пирсон)
20

21. Системы случайных величин

совместная функция распределения
F ( x, y ) P x, y
совместная ПРВ
2 F ( x, y )
w( x, y)
x y
x y
F ( x, y )
w( x, y)dxdy
21

22.

F ( , ) 0
Свойства ФР
F ( , ) 1
не убывает по
каждому аргументу
Свойства ПРВ
w( x, y) 0
w( x, y)dxdy 1
22

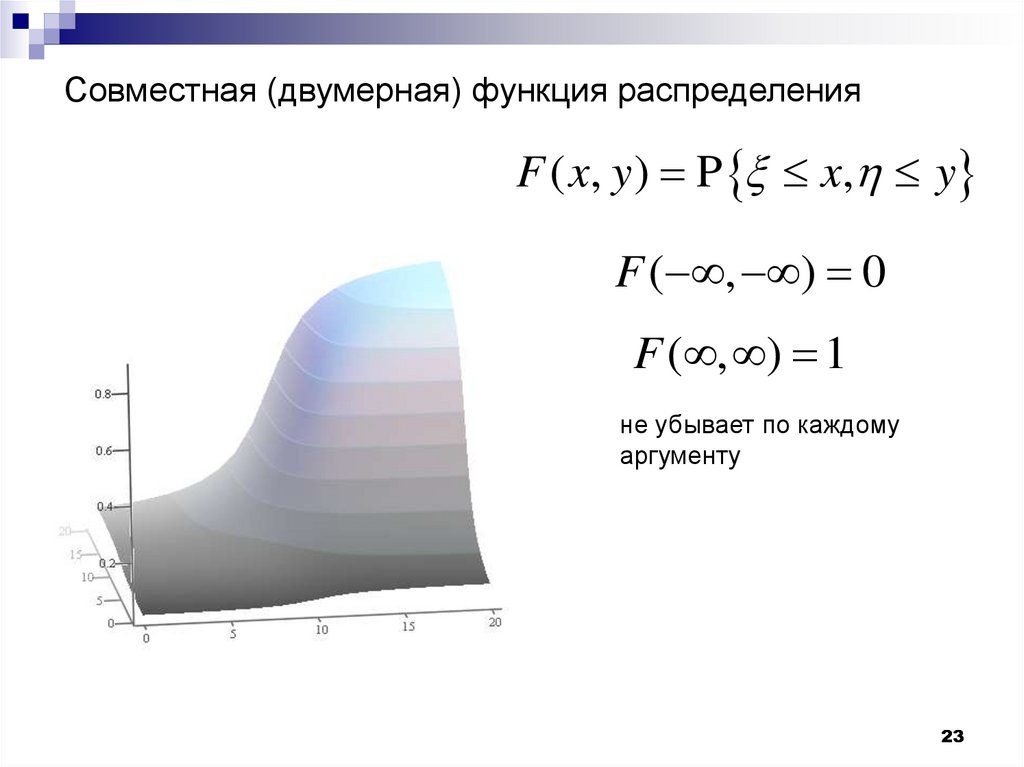
23.

Совместная (двумерная) функция распределения
F ( x, y ) P x, y
F ( , ) 0
F ( , ) 1
не убывает по каждому
аргументу
23

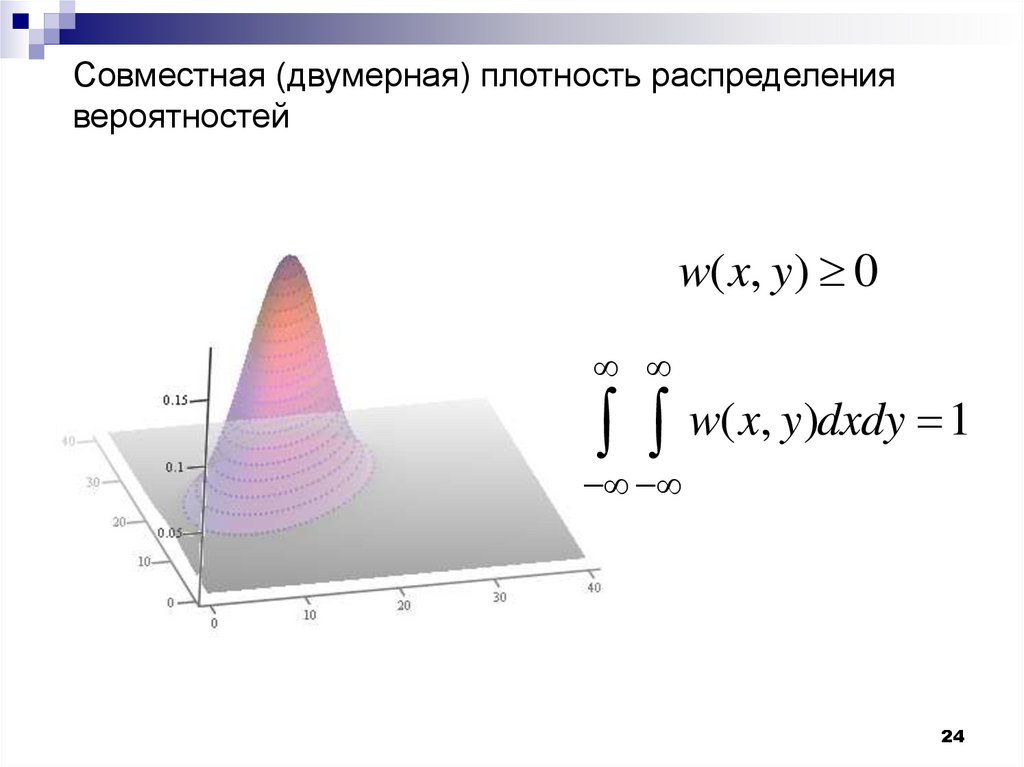
24.

Совместная (двумерная) плотность распределения
вероятностей
w( x, y) 0
w( x, y)dxdy 1
24

25.

x y
F ( x, y )
w( x, y)dxdy
F ( x, y )
w( x, y)
x y
2
25

26. Числовые характеристики системы 2 случайных величин

Начальные смешанные
моменты
mkn
x y w( x, y)dxdy
k n
Центральные смешанные
моменты
M kn ( x mx )k ( y m y )n w( x, y )dxdy
26

27.

m11
xyw
(
x
,
y
)
dxdy
k
xy
корреляционный момент
M11
( x mx )( y my )w( x, y)dxdy Rxy
ковариационный момент
27

28. Пример. Пара гауссовских случайных величин

( x1 m1 ) 2
( x1 m1 )( x2 m2 ) ( x2 m2 ) 2
2r
2
2
2
2(1 r ) 1
2
1 2
e
1
w( x1, x2 )
r
1
2 1 2 1 r 2
( x1 m1)( x2 m2 )
1 2
Rx1x2
коэффициент корреляции
1 2
При нулевом коэффициенте корреляции
1
w( x1, x2 )
e
2 1
( x m1 )2
2 12
1
2 2
e
( x m2 ) 2
2 22
w( x1) w( x2 )
Некоррелированные гауссовские с.в. – независимы!
28

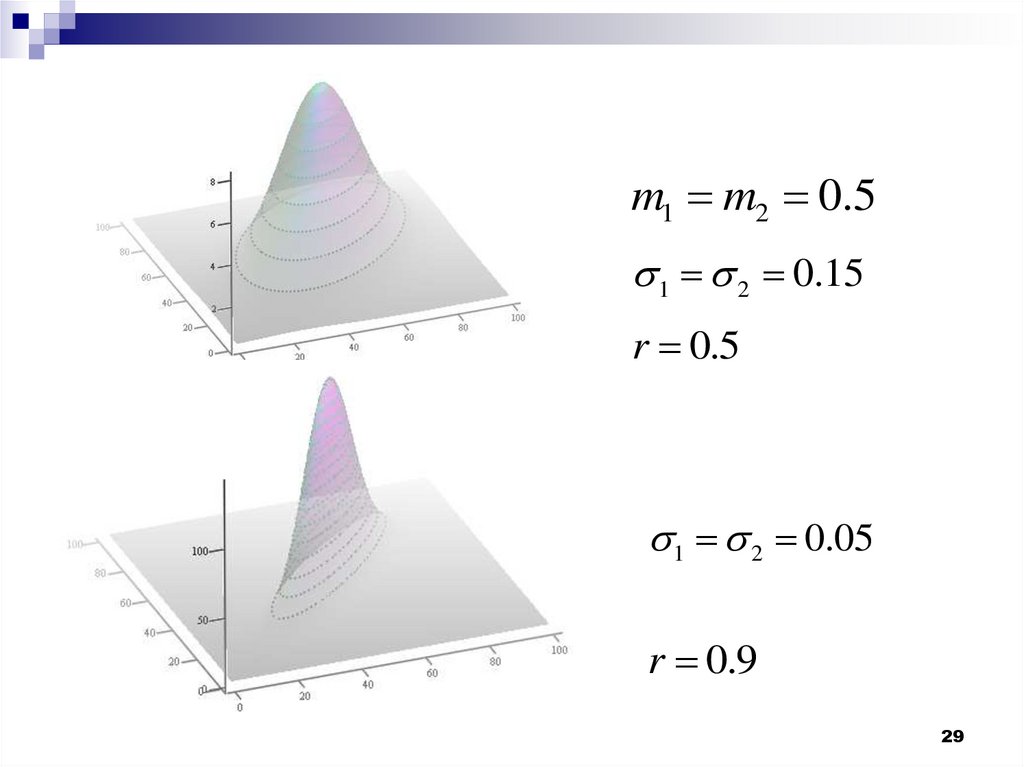
29.

m1 m2 0.5
1 2 0.15
r 0.5
1 2 0.05
r 0.9
29

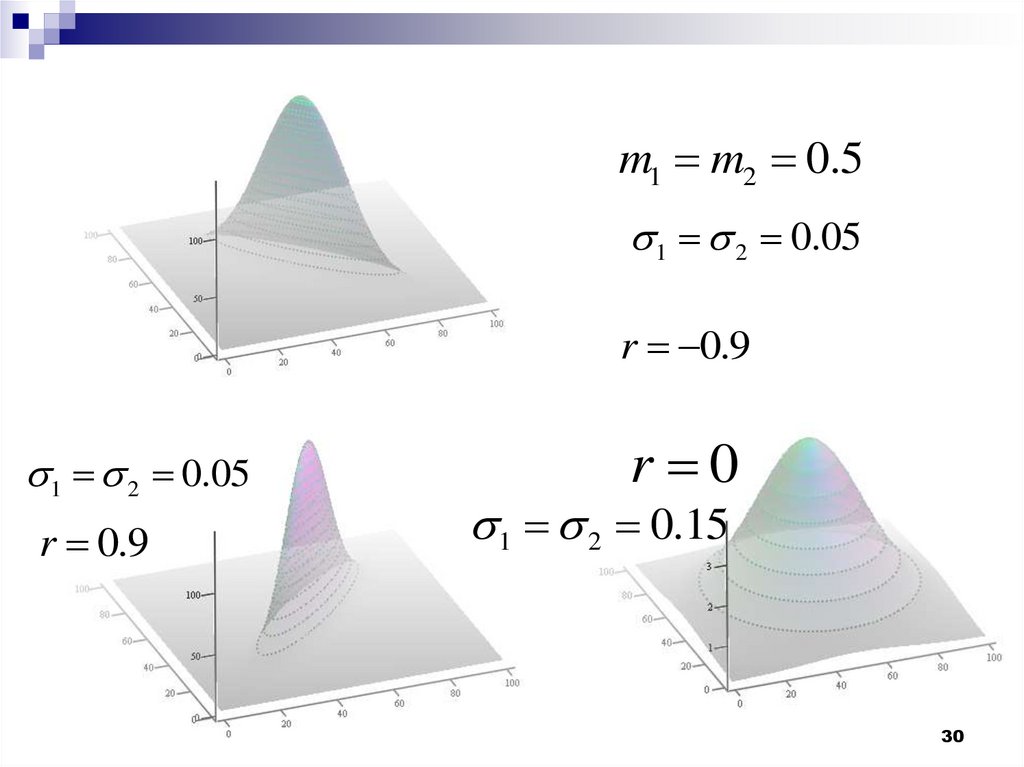
30.

m1 m2 0.5
1 2 0.05
r 0.9
1 2 0.05
r 0.9
r 0
1 2 0.15
30