Случайные величины. Определение случайной величины (лекция 6)

1.

СЛУЧАЙНЫЕ ВЕЛИЧИНЫ
Лекция 6

2. Определение случайной величины

• Случайная величина – это величина,
принимающая в результате испытания
одно из возможных значений, при этом
появление того или иного значения
является случайным событием.
• Различают дискретные и непрерывные
случайные величины.

3. Дискретная случайная величина и способы ее задания

Дискретной случайной величиной называется
случайная величина с конечным количеством
возможных значений.
Для определения дискретной случайной величины
задают закон ее распределения (ряд распределения), то есть все возможные значения
случайной величины и соответствующие им
вероятности:

4. Дискретная случайная величина и способы ее задания

• События, заключающиеся в том, что появится одно из
возможных значений случайной величины, являются
несовместными и образуют полную группу событий.
Сумма вероятностей полной группы событий равна
единице:
n
P
Pi x 1
i
i 1
P3
P4
P2
P1
P5
P6
xi
0
x1 x2
x3
x4
x5
x6
Графическое изображение дискретной случайной величины в
виде многоугольника распределения.

5. Числовые характеристики дискретной случайной величины

• Математическое ожидание
n
( X ) xi pi x1 p1 ... xn pn
• Дисперсия
i 1
D( X ) ( X ) ( ( X ))
2
, где ( X 2 ) xi2 Pi
n
2
• Среднее квадратичное отклонение
( X ) D( X )
i 1

6. Основные законы распределения дискретных случайных величин

• Формула Бернулли: Pn x
Cnx p x q n x
n!
p x q n x
x! n x !
P А p , P А q
• Совокупность полученных вероятностей
Рn(0), Рn(1), Рn(2), …,Рn(n) представляет
собой биномиальное распределение.

7. Основные законы распределения дискретных случайных величин

• Формулу Муавра-Лапласа используют для схемы
n 10 p 0,1
Бернулли, когда
Вероятности определяют по формулам:
а)
Pn ( X x)
1
e
2 npq
1 x np
2 npq
2
- локальная формула Лапласа;
2
б) P ( x X x ) 1
n
1
2
2
z2 z
e 2
z1
x 2 np
x1 np
dz (
) (
)
npq
npq
- интегральная формула Лапласа, где Ф(z)- интегральная
функция Лапласа

8. Основные законы распределения дискретных случайных величин

• При тех же условиях, но когда n 10 и p 0,1
применяют формулу Пуассона:
где np
Pn x
x
x!
• При этом:
X D X ;
e
,

9. Непрерывная случайная величина. Способы ее задания

• Непрерывной случайной величиной называется случайная
величина, которая может принимать любое значение из
некоторого интервала (на котором она существует).
• Интегральная функция распределения непрерывной
x
случайной величины:
F ( x) P( X x)
f ( x)dx
• Дифференциальная функция распределения
непрерывной случайной величины (функция
плотности распределения):
dP
f ( x)
F ( x)
dx

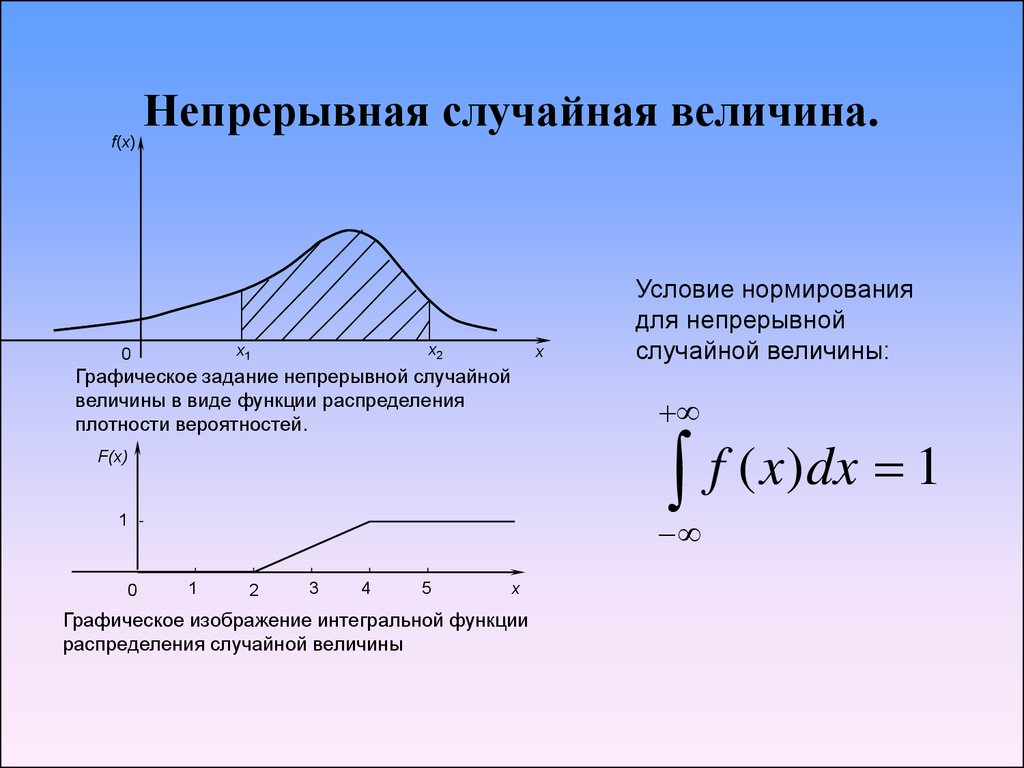
10. Непрерывная случайная величина.

f(x)
Непрерывная случайная величина.
x2
x1
0
x
Графическое задание непрерывной случайной
величины в виде функции распределения
плотности вероятностей.
f ( x)dx 1
F(x)
1
0
Условие нормирования
для непрерывной
случайной величины:
1
2
3
4
5
x
Графическое изображение интегральной функции
распределения случайной величины

11. Числовые характеристики непрерывной дискретной случайной величины

x
Математическое ожидание:
( X ) x f ( x )dx
2
x1
• Дисперсия:
где
D( X ) ( X 2 ) ( ( X )) 2
x2
( X 2 ) x 2 f ( x )dx
x1
• Среднее квадратичное отклонение:
( X ) D( X )
• Вероятность попадания в промежуток:
P( x1 X x 2 )
x2
f ( x)dx F ( x2 ) F ( x1 )
x1

12. Основные законы распределения непрерывных случайных величин

• 1. Равномерное распределение:
Дифференциальная функция
распределения -
Интегральная функция
распределения -
x a;
0,
1
f ( x)
, a x b;
b a
x b.
0,
x a;
0,
x a
F ( x)
, a x b;
b a
x b.
1,

13. Основные законы распределения непрерывных случайных величин

• 2. Показательное (экспоненциальное)
распределение непрерывной случайной
величини з параметром .
Дифференциальная функция
распределения –
Интегральная функция
распределения -
x 0;
0,
f ( x ) x
e , x 0.
x 0;
0,
F ( x) x
1 e , x 0.

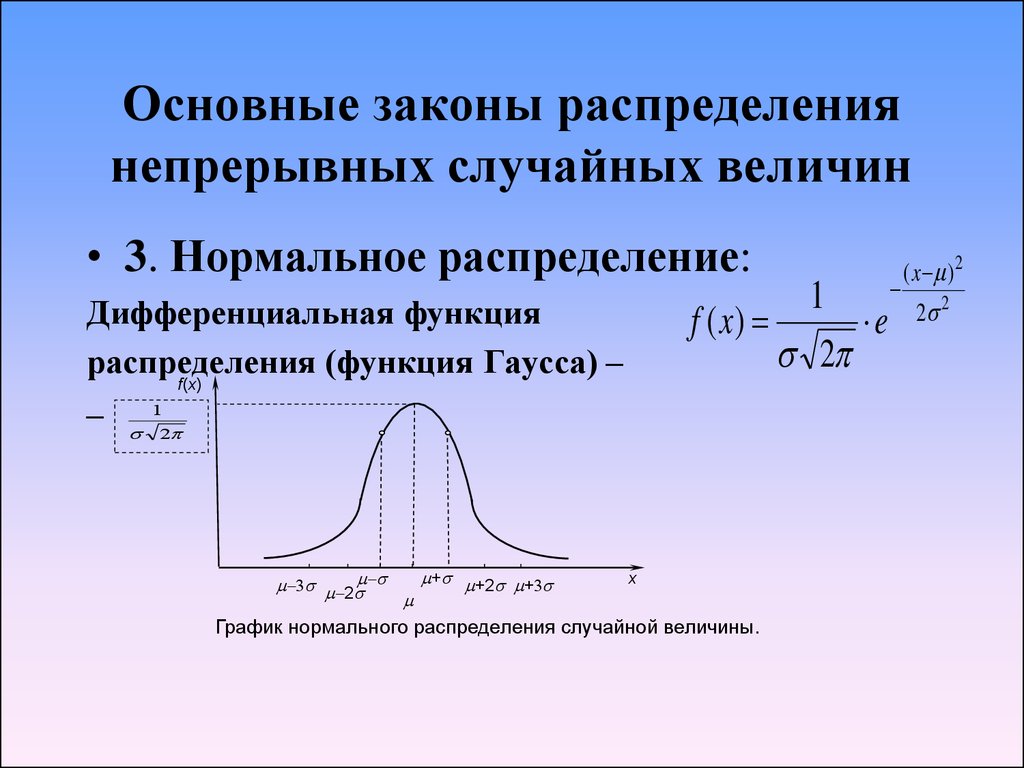
14. Основные законы распределения непрерывных случайных величин

• 3. Нормальное распределение:
1
f ( x)
e
2
Дифференциальная функция
распределения
(функция Гаусса) –
f(x)
–
1
2
+ +2 +
2
x
График нормального распределения случайной величины.
( x )2
2 2

15. Стандартная функция Лапласа

• Если в функции Гаусса взять 0 и 1 , то
получим нормированную или стандартную функцию
(дифференциальную функцию).
( z)
1
e
2
z2
2

16. Основные законы распределения непрерывных случайных величин 3. Нормальное распределение

• Вероятность попадания нормально распределенной
случайной величины в интервал определяется по
формуле:
x2
x1
P( x X x )
1
1
2
z
z2
e 2 dz
2
где
- интегральная функция
Лапласа, ее значения находятся по таблице.
( z )
• Правило трех сигм: если случайная величина
нормально распределена, то практически достоверно,
то есть с вероятностью, близкой к единице, ее
значения лежат на промежутке [ .