Similar presentations:
Случайная величина
1. Случайная величина.
Случайной называется величина, которая может в результатеопыта принимать то или иное числовое значение, заранее
неизвестно, какое именно.
Случайные величины обозначаются X, Y, Z, а их возможные
значения x, y, z.
Примеры.
Случайные величины бывают двух типов: дискретные и
непрерывные.
Дискретной называется случайная величина, если число ее
возможных значений конечно или счетно (т.е. их можно
пересчитать).
Дискретная случайная величина принимает отдельно
стоящие значения.
2. Случайная величина называется непрерывной, если
ее возможные значения целиком заполняют некоторыйинтервал, конечный или бесконечный.
Пример 1. Производится залп из пяти орудий. Случайная
величина X – число попаданий в цель. Ее
возможные значения : 0, 1, 2, 3, 4, 5. X – дискретная
случайная величина.
Пример 2. Испытывается машина.
Случайная величина T – время работы двигателя
от момента включения до его поломки.
Возможные значения T: 0 T . T – непрерывная
случайная величина.
3. Законом распределения (рядом распределения) дискретной случайной величины называется соответствие между ее
возможными значениями и ихX
вероятностями:
x1
x2
…
xn
P
p1
p2
…
pn
Так как события X x1 , X x 2 , ..., X x n
n
полную группу, то pi 1.
i 1
образуют
4. Пример 1.
Бросают одновременно триX
0
монеты. Случайная величина
X – число появлений герба.
1
Составить закон
P
8
распределения X.
Применяем формулу
Бернулли: Pn (m) C mn p m q n m , где n = 3,
p
1
2
3
3
8
3
8
1
8
1 - вероятность появления герба при одном бросании
2 монеты, q = 1 – p = 1 .
2
5. Вычисления:
03
2
1
3
0
1
1
1
P3 (0) C30 ,
2 2 8
1
2
1
1
3
P3 (1) C13 ,
2 2 8
1
1
3
P3 (2) C32 ,
2 2 8
1
3 1 1
P3 (3) C3 .
2 2 8
4
1 3 3 1
pi 1.
8 8 8 8
i 1
6. Пример 2.
В магазин вошли два покупателя. Вероятность того, чтопервый покупатель сделает покупку, равна 0,7. Для
второго – вероятность сделать покупку 0,8 . Составить
закон распределения числа сделанных покупок.
Решение.
Случайная величина X – число сделанных покупок.
Ее возможные значения: 0, 1, 2.
Соответствующие вероятности:
P(X 0) 0,3 0,2 0,06;
P(X 1) 0,7 0,2 0,3 0,8 0,38;
P(X 2) 0,7 0,8 0,56.
Проверка: 0,06 + 0,38 + 0,56 = 1.
7. Составляем закон распределения случайной величины X:
X0
1
2
P
0,06
0,38
0,56
8.
Для непрерывной случайной величины закон распределениязадать нельзя, так как невозможно выписать все ее значения.
Функция распределения случайной величины.
Функцией распределения случайной величины называется
функция F (x), которая равна вероятности того, что
случайная величина X примет значение, меньшее аргумента x,
т.е.
F( x ) P(X x ).
Или
F( x ) P[X ( ; x )].
9. Свойства функции распределения.
1). 0 F( x ) 1для всех x. (Это следует из определения).
2). F (x) – неубывающая функция, так как
x 2 x1 F(x 2 ) F( x1 ).
Действительно,
F(x 2 ) P(X x 2 ) P(X x1 ) P(x1 X x 2 )
F( x1 ) P(x1 X x 2 ),
То есть F(x 2 ) F(x1 ).
10.
3). Вероятность попадания X в интервал от x1 до x 2 равнаразности значений функции распределения этой
случайной величины.
P(x1 X x 2 ) F(x 2 ) F(x1 ).
4). lim F( x ) 0, так как P(x - ) 0 (невозможное событие).
x
lim F(x) 1, так как P(x ) 1.
x
11. Примеры функций распределения.
1). Функция распределениядискретной случайной
величины (пример 2).
1). x 0
X
P
0
0,06
1
0,38
2
0,56
F( x ) P(X x ) 0;
2). 0 x 1 F( x ) P(X x ) P(X 0) 0,06
3). 1 x 2 F( x ) P(X x ) P(X 0) P(X 1) 0,06 0,38 0,44
4). x 2 F( x ) P(X x ) P(X 0) P(X 1) P(X 2) 0,06 0,38 0,56 1
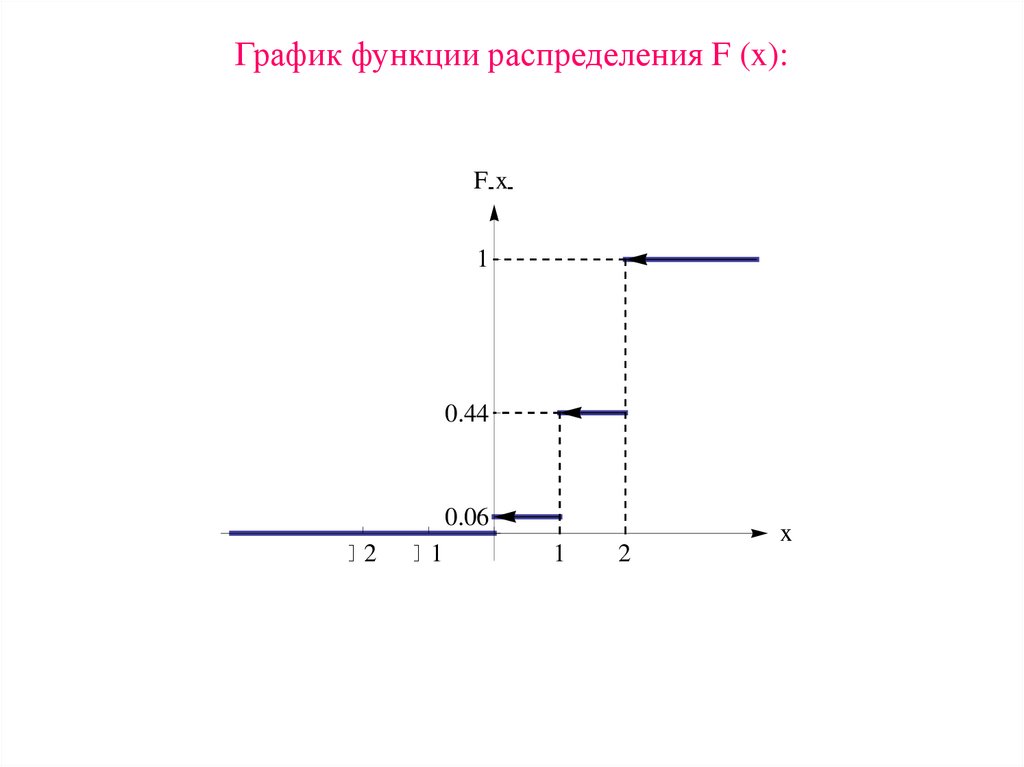
12. Таким образом, получили функцию распределения:
0, если x 0 ;0,06, если 0 x 1;
F( x )
0,44, если 1 x 2 ;
1, если x 2
13. График функции распределения F (x):
Fx1
0.44
0.06
2
1
1
2
x
14. Второе определение непрерывной случайной величины:
Случайная величина, у которой функция распределениянепрерывна и имеет кусочно-непрерывную производную,
называется непрерывной случайной величиной.
Вероятность того, что непрерывная случайная
величина примет одно определенное значение, равна
нулю.
Доказательство.
В свойстве 3 функции распределения
P(x1 X x 2 ) F(x 2 ) F(x1 )
возьмем x 2 x1 x
и перейдем к пределу при x 0 :
lim P(x1 X x1 x) lim F(x1 x) F(x1 ) lim F 0,
x 0
x 0
x 0
так как F (x) –непрерывная функция. Следовательно, P(X x1 ) 0.
15. Тогда справедливы равенства:
P(x1 X x 2 ) P(x1 X x 2 ) P(x1 X x 2 ) P(x1 X x 2 ).Например, равенство P(x1 X x 2 ) P(x1 X x 2 )
доказывается так:
P(x1 X x 2 ) P(x1 X x 2 ) P(X x1 ) P(x1 X x 2 ),
так как P(X x1 ) 0.
16.
Таким образом, не представляет интереса говорить овероятности того, что непрерывная случайная величина
примет одно определенное значение, но имеет смысл
рассматривать вероятность попадания ее в интервал.
Например, интересуются вероятностью того, что размеры
деталей не выходят за дозволенные границы, но не ставят
вопроса о вероятности их совпадения с проектным размером.
17. Плотность распределения вероятностей непрерывной случайной величины.
Плотностью распределения вероятностейнепрерывной случайной величины называется
функция f (x) – первая производная функции
распределения F (x)
F ( x ) f ( x ) - плотность распределения
случайной величины.
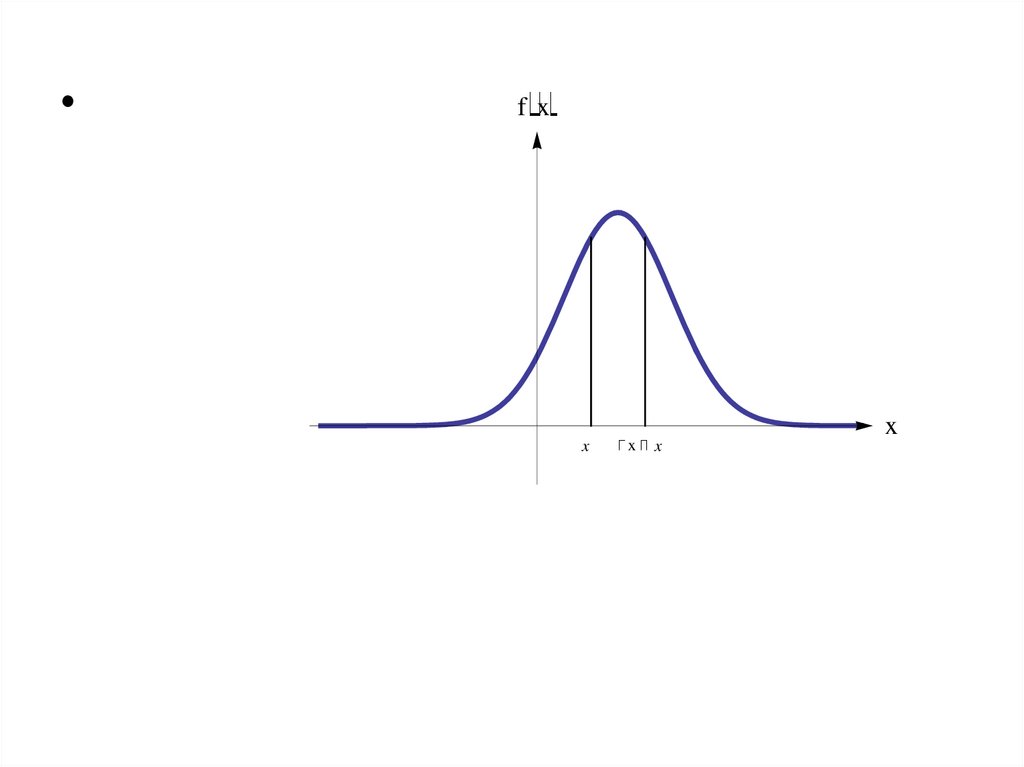
18. Вероятностный смысл плотности вероятности.
P( x X x x ) F( x x ) F( x ) dF( x ) F ( x ) x f ( x ) x,то есть вероятность того, что случайная величина примет
значение из интервала ( x, x x ) приблизительно равна
плотности вероятности, умноженной на длину интервала x.
19.
fx
x
x
x
x
20. Свойства плотности распределения.
1). Плотность распределения – неотрицательная функция: f ( x ) 0.Доказательство.
x
2).
F( x ) f ( x ) dx.
Доказательство.
x
x
x
f (x ) dx F (x ) dx lim F(x ) F(x ) lim F(A) F(x ).
A
A
A
3). Вероятность попадания случайной величины в заданный интервал.
P( X ) f ( x ) dx
Доказательство.
P( X ) F( ) F( ) f ( x ) dx f ( x ) dx f ( x ) dx
21.
4).f (x ) dx 1.
Доказательство.
f ( x ) dx
это вероятность того, что случайная величина
примет значение, принадлежащее интервалу ( , )
- это достоверное событие, следовательно, его вероятность равна 1.
В частности, если все возможные значения случайной величины
принадлежат интервалу (a, b), то b
f (x) dx 1.
a




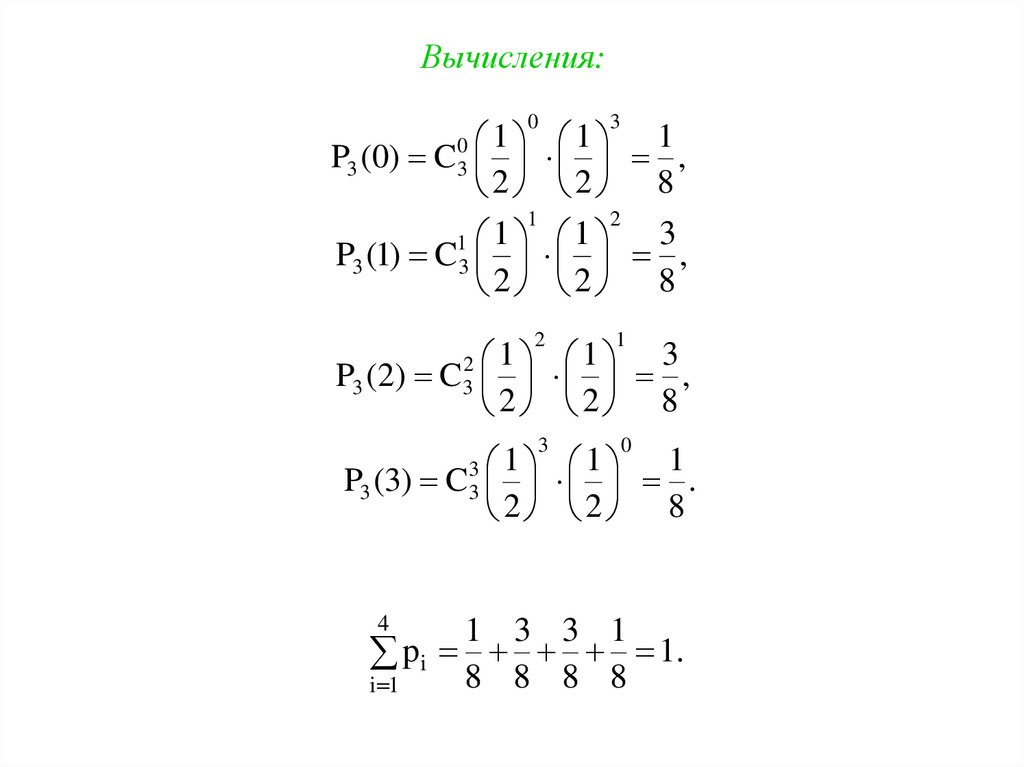














 mathematics
mathematics








