Основные понятия теории случайных процессов

1.

Статистическая
радиофизика
Курс лекций для бакалавров направления
03.03.03 -- «Радиофизика», 7 семестр
2022-2023 учебный год

2.

Основные понятия теории случайных
процессов
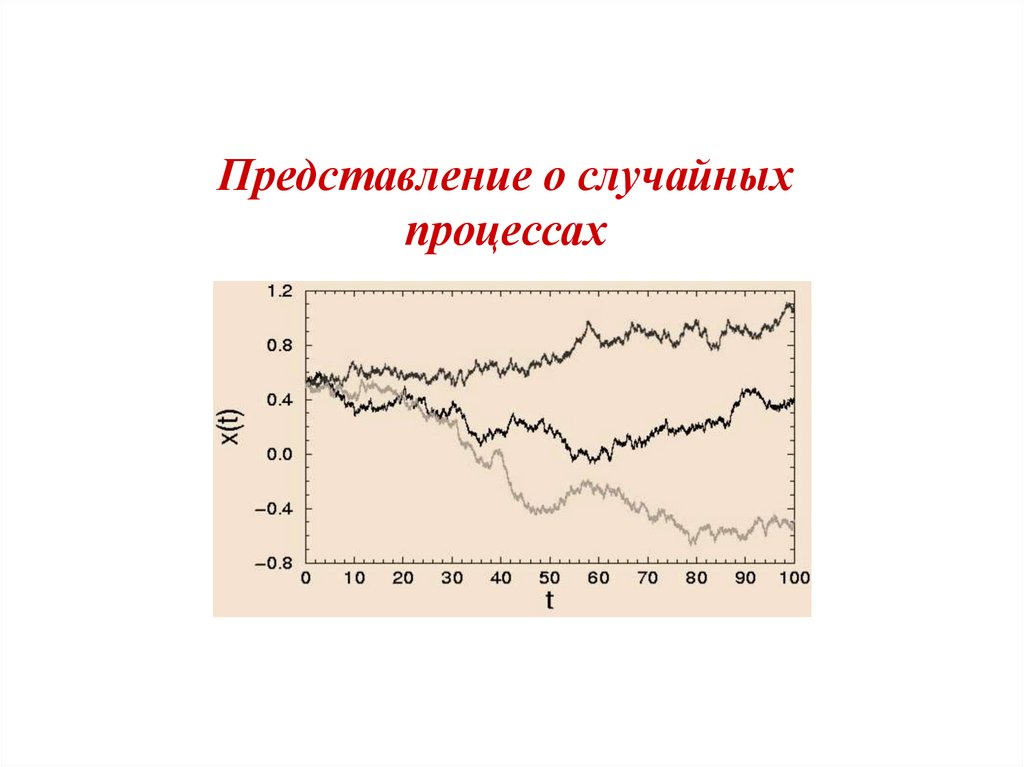
Представление о случайных процессах
Статистические характеристики случайных процессов
Стационарные случайные процессы
Процеесы с перемешиванием. Время корреляции

3.

Представление о случайных
процессах

4.

Понятие случайного процесса
Случайный (стохастический) процесс – это процесс изменения
состояния системы во времени, протекающий по вероятностным
(статистическим) законам.
Типичным примером СП. может служить броуновское движение.
Другими практически важными примерами являются процессы в
электрических
цепях
при
наличии
неупорядоченных флуктуаций напряжения и силы тока
(шумов),
распространение радиоволн в турбулентной атмосфере, случайные
замирания (фединги) радиосигналов, создаваемые метеорологическими
или иными помехами. К числу СП может быть причислен также ряд
процессов, встречающихся в геофизике (например, вариации магнитного
поля земли), физиологии (например, изменение биоэлектрических
потенциалов мозга, регистрируемое на электроэнцефалограмме) и
экономике (например, изменение курсов валют).

5.

Пусть множество M есть множество значений случайной величины X (т.е.
пространство состояний системы). В каждый момент времени величина X
случайным образом принимает некоторое значение x M.
Величина X может быть векторной, скалярной, вещественной или
комплексной.
Случайный процесс описывается случайной функцией X (t), принимающей
значения во множестве M. Аргумент t – время.
Для любого фиксированного t0 значение -- случайная величина. X0 = X (t0).
Реализации случайного процесса
Реализация случайного процесса –-- это детерминированная функция x(t),
получаемая в результате измерения. Имеется статистический ансамбль
реализаций случайного процесса.
Далее будем в основном рассматривать вещественные скалярные случайные
процессы X (t) .

6.

Классификация случайных процессов
1. По множеству значений, принимаемых переменными X и t .
Множество состояний M может быть дискретным (конечным или счетным)
или непрерывным. Время t может принимать непрерывное или счетное
множество значений. Различают:
• непрерывнозначные случайные процессы (M и t – непрерывные);
• дискретные случайные процессы (M – дискретное, t - непрерывное);
• непрерывные случайные последовательности (M – непрерывное, t –
дискретные);
• дискретные случайные последовательности (M и t – дискретные).
(а)
(б)
(в)
(г)
Типичные реализации:
а – непрерывнозначный сл.
процесс;
б – дискретный сл.
процесс;
в – непрерывная сл.
последовательность;
г – дискретная сл.
последовательность

7.

2. По признаку сохранения во времени некоторых свойств процесса
различают стационарные и нестационарные процессы.
3. По признаку заменяемости усреднения по ансамблю реализаций
усреднением по времени различают эргодические и неэргодические
процессы.
4. По свойствам спектра различают узкополосные случайные процессы,
широкополосные случайные процессы, белый шум.
5. По виду закона распределения вероятностей выделяют нормальные
(гауссовы) процессы.
6. По характеру влияния предыстории процесса выделяют марковские
процессы.

8.

Квазидетерминированные случайные процессы
Выделяют также так называемые квазидетерминированные случайные
процессы.
Случайный процесс X(t) называют квазидетерминированным, если он
описывается детерминированной функцией времени, которая содержит
параметры, являющиеся случайными величинами:
X (t ) f (t , ),
f(…) детерминированная функция аргумента t, -- параметр, задаваемый
случайной величиной. Каждому возможному значению случайного
параметра * соответствует реализация процесса:
x (t ) f (t , )
Реализации квазидетерминированного процесса – регулярные функции
(например, гармонические). Однако процесс является случайным, т.к.
заранее его реализация неизвестна.

9.

Статистические характеристики
случайных процессов
p n ( x1 , t1 , x 2 , t 2 ,
x n , t n ) dx1 dx 2
P{ X (t1 ) [ x1 , x1 dx1 )
dx n
X (t n ) [ x n , x n dx n )}.

10.

Дискретная случайная величина X={xi} полностью характеризуется
вероятностями Pi=P {xi}:
Pi 0, Pi 1.
i
Непрерывная случайная величина
плотностью вероятности p(x):
X
полностью
характеризуется
p ( x) 0,
p(x)dx 1
-
Рассмотрим непрерывнозначный процесс X(t). В каждый момент времени
его можно охарактеризовать плотностью вероятности p(x,t). В общем
случае она зависит от времени.
p(x,t)
x
Однако функция p(x,t) не может полностью характеризовать процесс, т.к.
не показывает степень взаимосвязи значений в разные моменты времени.

11.

n–мерная плотность вероятности случайного процесса
p n ( x1 , t1 , x 2 , t 2 , x n , t n ).
Пусть X (t) – вещественный скалярный непрерывнозначный случайный
процесс. Он характеризуется n – мерной плотностью вероятности:
p n ( x1 , t1 , x2 , t 2 ,
dxn
xn , t n ) dx1 dx2
P{ X (t1 ) [ x1 , x1 dx1 )
X (t n ) [ xn , xn dx n )}.
n -- число рассматриваемых моментов времени,
P{…} – вероятность события, обозначенного в фигурных скобках.
Для плотности вероятности pn (…) можно также записать
pn ( x1 , t1 , x2 , t2 , xn , tn )
lim
i xi 0
P{ X (t1 ) [ x1 , x1 x1 ) X (t n ) [ xn , xn xn )}
n
xi
i 1
.

12.

Свойства плотности вероятности случайного процесса
1. Неотрицательность:
2. Нормировка:
pn ( x1 , t1 , xn , tn ) 0.
p (x ,t ,
n
1
dxn 1.
xn , t n )dx1
1
3. Согласование:
k n pk ( x1 , t1 , xk , tk )
p ( x , t , x , t )dx
n
1 1
n
n
k 1
dxn .
4. Инвариантность относительно перестановки пар аргументов:
i, k n pn ( x1 , t1 , , xi , ti , xk , tk , xn , tn ) pn ( x1 , t1 , , xk , tk , xi , ti , xn , tn ).
5. Если значения процесса в некоторые моменты времени ti0, i =1,…n
статистически независимы, то
0
1
pn ( x1 , t ,
n
xn , t ) p1 ( xi , ti0 ).
0
n
i 1

13.

Функция распределения случайного процесса
Fn ( x1 , t1 , x n , t n ).
x1
Fn ( x1 , t1 ,
xn , t n )
xn
p ( x , t , x , t )dx dx .
n
1 1
n
n
1
Обратно:
n Fn ( x1 , t1 , xn , t n )
p n ( x1 , t1 , xn , t n )
.
x1 xn
n

14.

Характеристическая функция случайного процесса
X ( u 1 , t1 , u n , t n ).
X (u1 , t1 ,
u n , tn )
p (x ,t ,
n
1
1
n
xn , t n ) exp j xi u i dx1
i 1
dx n .
Обратно:
1
p n ( x1 , t1 , xn , t n )
(2 ) n
n
(
u
,
t
,
u
,
t
)
exp
j
x
u
X 1 1 n n i 1 i i du1 du n .
Случайный процесс X(t) полностью задан, если n известна одна из
функций:
• плотность вероятности pn ( x1 , t1 , xn , tn );
• функция распределения Fn ( x1 , t1 , xn , tn );
• характеристическая функция (u , t , u , t ).
X
1 1
n n
В этом случае можно найти все статистические характеристики
случайного процесса.

15.

Моментные функции случайного процесса
Усреднение по ансамблю реализаций случайного процесса
f ( X (t1 ),
X (tn ))
p ( x , t , x , t ) f ( x , x )dx
n
1
1
n
n
1
n
1
dxn f (t1 , t n ).
где f (…) – детерминированная функция своих аргументов.
Начальные моменты:
k
X (ti )
ri
i 1
p k ( x1 , t1 ,
x k , t k )x1r1
x krk dx1
k
r ri
i 1
– порядок момента, k – размерность момента.
dx k .

16.

Центральные моменты:
k
X (ti )
ri
i 1
r1
p
(
x
,
t
,
x
,
t
)(
x
X
(
t
))
k 11 k k 1 1
( xk X (t k )) rk dx1
dx k .
X (t ) X (t ) p1 ( x , t )xdx
-- среднее значение случайного процесса,
X (t ) X (t ) X (t ) -- флуктуации относительно среднего значения.
Основные моменты
Дисперсия случайного процесса (центральный одномерный момент
второго порядка):
X2 (t ) ( X (t ) X (t )) 2 p1 ( x , t )( x X (t )) 2 dx.
Легко видеть, что: X2 ( t ) X 2 ( t ) X 2 ( t ).
X (t ) X2 (t )
-- среднеквадратическое отклонение.

17.

Ковариационная функция случайного процесса (начальный двумерный
момент второго порядка):
K X (t1 , t 2 ) X (t1 ) X (t 2 ) p 2 ( x1 , t1 , x2 , t 2 )x1 x2 dx1 dx2 .
Корреляционная (автокорреляционная) функция случайного процесса
(центральный двумерный момент второго порядка):
X (t1 , t2 ) ( X (t1 ) X (t1 )( X (t 2 ) X (t 2 ))
p2 ( x1 , t1 , x2 , t 2 )( x1 X (t1 ))( x2 X (t 2 )) dx1dx2 .
Легко видеть, что:
X (t1 , t 2 ) X (t1 ) X (t 2 ) X (t1 ) X (t 2 ).
Замечание: Иногда применяется другая терминология: центральный момент
называют ковариационной функцией, а начальный – корреляционной.

18.

Коэффициент корреляции (нормированная корреляционная функция):
RX (t1 , t2 )
X (t1 , t2 )
(t1 ) (t2 )
2
X
2
X
.
Свойства корреляционной функции случайного процесса
1. -- 2X (t1 , t 2 ) X2 (t1 ) X2 (t 2 ),
2. -- X (t , t ) X2 (t ),
3. -- X (t1 , t2 ) X (t2 , t1 ),
Если значения случайного процесса в моменты времени
t = t‘1 и t = t‘2
статистически
независимы, то они
некоррелированы, т.е. X (t1 , t2 ) 0. Обратное не всегда верно.
4. --

19.

Пример: Реализации процесса с одним значением дисперсии и
различной корреляционной функцией
X (t ) (t )
X (t )
X (t ) (t )
X (t )
X (t ) (t )
Более сильная корреляция
значений в разные моменты
времени
X (t ) (t )
Более слабая корреляция
значений в разные моменты
времени

20.

Связь начальных моментов процесса с
характеристической функцией
Начальные моменты случайного процесса являются коэффициентами в
разложении n-мерной характеристической функции в ряд Маклорена:
X (u1 , t1 , u2 , t2 ,... un , tn )
X r1 (t1 ) X r2 (t2 )... X rn (tn )
...
( ju1 )r1 ( ju2 ) r2 ...( jun ) rn
r1 !r2 !... rn !
r1 0 rn 0
и, соответственно, могут быть найдены по формуле
X r1 (t1 ) X r2 (t2 )... X rn (tn )
r
n
X (u1 , t1 , u2 , t2 ,... un , tn )
r
( j )
, где r ri .
rn
r1
r2
u1 u2 ... un
i 1
u u ... u 0
1
2
n

21.

Стационарные случайные
процессы
p n ( x 1 , t1 T , , x n , t n T ) p n ( x 1 , t 1 , , x n , t n )

22.

Стационарность случайного процесса означает, что стохастическая
система находится в установившемся состоянии и ее статистические
характеристики не меняются во времени.
1. Случайный процесс X (t) называется стационарным в строгом (узком)
смысле, если для любого n, любой константы T и любых моментов
времени ti , i=1,2,… n имеет место равенство
pn ( x1 , t1 T , , xn , tn T ) pn ( x1 , t1 , , xn , tn ),
что означает инвариантность плотности вероятности (и, следовательно,
всех статистических характеристик) относительно сдвига во времени.
2. Случайный процесс X(t) называется стационарным в широком
смысле, если выполняются условия
X const X (t1 , t2 ) X (t2 t1 ) X 2 .

23.

Свойства корреляционной функции стационарного процесса
1. --
X ( ) X2 , где = t2 – t1 ,
2. -- X (0) X2 ,
3. -- X ( ) X ( ),
Если корреляционная функция непрерывна при = 0, то она
непрерывна для любого .
4. --

24.

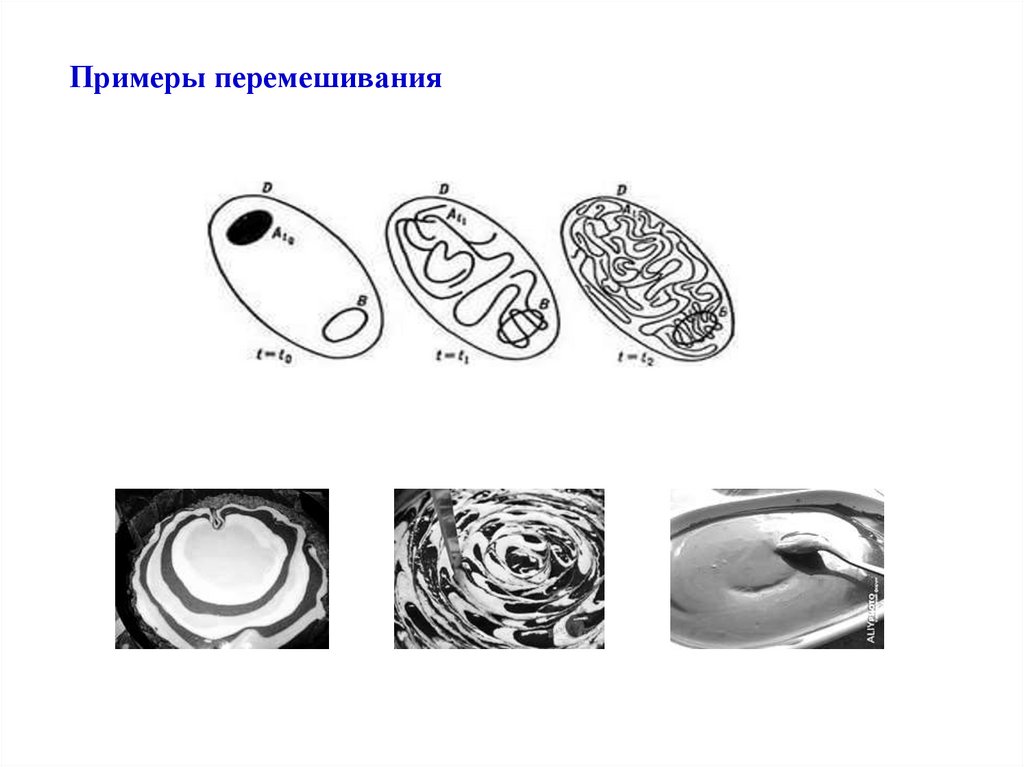
Процессы с перемешиванием.
Время корреляции

25.

Стационарный случайный процесс, для которого выполняется условие
lim X ( ) 0,
называется процессом с перемешиванием. Для него справедливо
lim p 2 ( x1 , x2 , ) p1 ( x1 ) p1 ( x2 ).
Чтобы охарактеризовать скорость перемешивания
корреляций) вводят время корреляции корр .
(расцепления
1. Время корреляции вводится как интервал, на котором огибающая
корреляционной функции X ( ) убывает в е раз.
X ( )
e.
X ( корр )
2
X
2.
корр
1
корр 2 X ( )d .
X 0
X ( )
или
1
корр 2 | X ( ) | d .
X 0

26.

Примеры перемешивания