Similar presentations:
Теория вероятностей и математическая статистика
1. Теория вероятностей и математическая статистика
2. Список литературы
1. Н.Н. Одияко, Н.Ю. Голодная. Теориявероятностей. Учебное пособие.
2. Н.Н. Одияко, Н.А. Бажанова. Обработка
одномерной выборки.
3. Н.Ю. Голодная, Н.Н. Одияко.
Математическая статистика. Теория
корреляции в расчетах. Часть2.
3.
4. В.Е. Гмурман. Теория вероятностей иматематическая статистика.
5. В.Е. Гмурман. Руководство к решению
задач по теории вероятностей и
математической статистике.
4. Основные понятия комбинаторики
5. Правило умножения
6.
• Пусть требуется выполнить одно задругим какие-то k действия. Если
первое действие можно выполнить n1
способом, второе действие - n2
способами, третье - n3 способами и т.д.
до k го действия, которое можно
выполнить n k способами, то все k
действий вместе быть выполнены
могут быть выполнены n1 n2 n3 ... nk
способами.
7. Правило сложения
8.
• Если два действия взаимно исключаютдруг друга , причём одно из них можно
выполнить m способами, а другое- n
способами, то выполнить одно любое из
этих действий можно n m способами.
Это правило распространяется на любое
конечное число действий.
9.
• Опр. Последовательностьэлементов называется
упорядоченной, если порядок
следования элементов в ней задан
10.
• Опр. Размещением из n элементов поm элементов называется любое
упорядоченное подмножество из m
элементов множества, состоящего из
различных элементов:
n
n!
A
(n m)!
m
n
11.
• Опр. Перестановками из nэлементов называется любое
упорядоченное множество,
в которое входят по одному разу
все n различные элементы
данного множества:
Pn n!
12.
• Опр. Сочетанием из n элементов по mэлементов называется любое
подмножество из m элементов, которые
принадлежат множеству, состоящему из
различных
элементов:
n
m
Cn
n!
m! n m !
13. СЛУЧАЙНЫЕ СОБЫТИЯ И ПРЕДМЕТ ТЕОРИИ ВЕРОЯТНОСТЕЙ
14.
Опр. Испытание (опыт, эксперимент)выполнение определенного комплексаусловий, в которых наблюдается то или
иное явление, фиксируется тот или иной
результат
15.
• Опр. Событие называется случайнымпо отношению к данному испытанию
(опыту), если при осуществлении этого
испытания (опыта) оно может наступить
или не наступить.
• Событие обозначается:
A, B, C,....
16.
Определения.1.Событие , которое в результате
опыта обязательно произойдет
называется достоверным.
2.Событие, которое в результате
опыта никогда не наступит называется
невозможным.
3. Если одновременно одно
событие влечет за собой другое и
наоборот, такие события называются
равносильными.
17.
4. События называются несовместными,если наступление одного из них исключает
наступление любого другого.
5. События называются
равновозможными, если в результате
испытания по условиям симметрии ни одно
из этих событий не является объективно
более возможным.
18.
6. События называютсяединственно возможными, если появление в
результате испытания одного и только
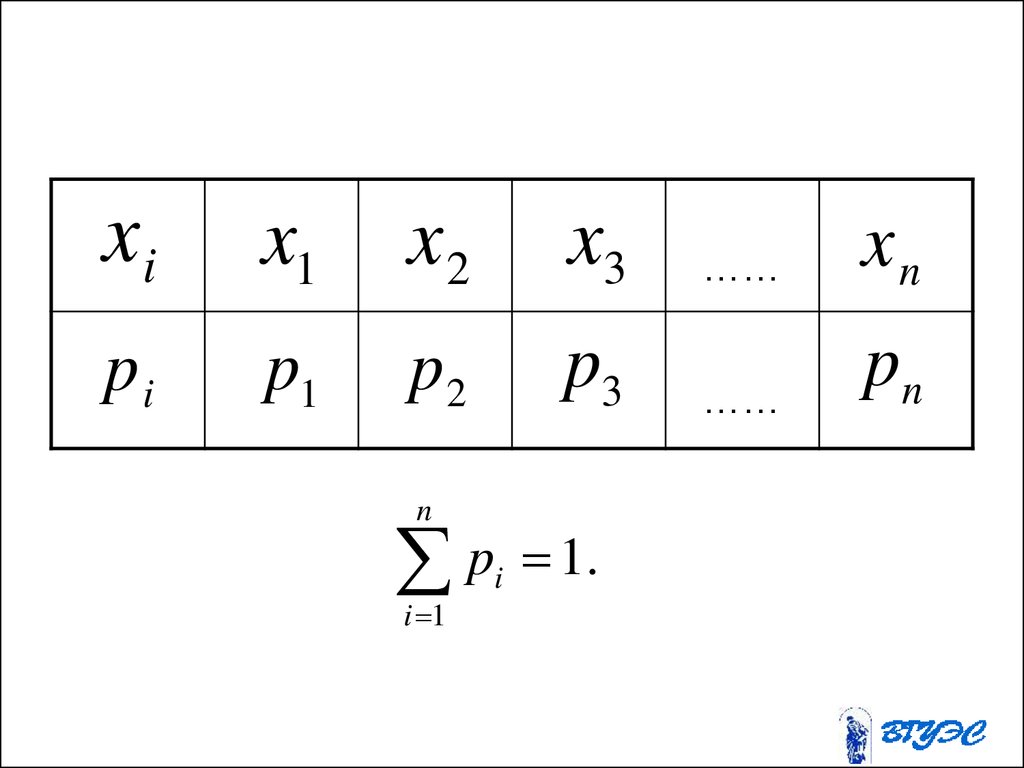
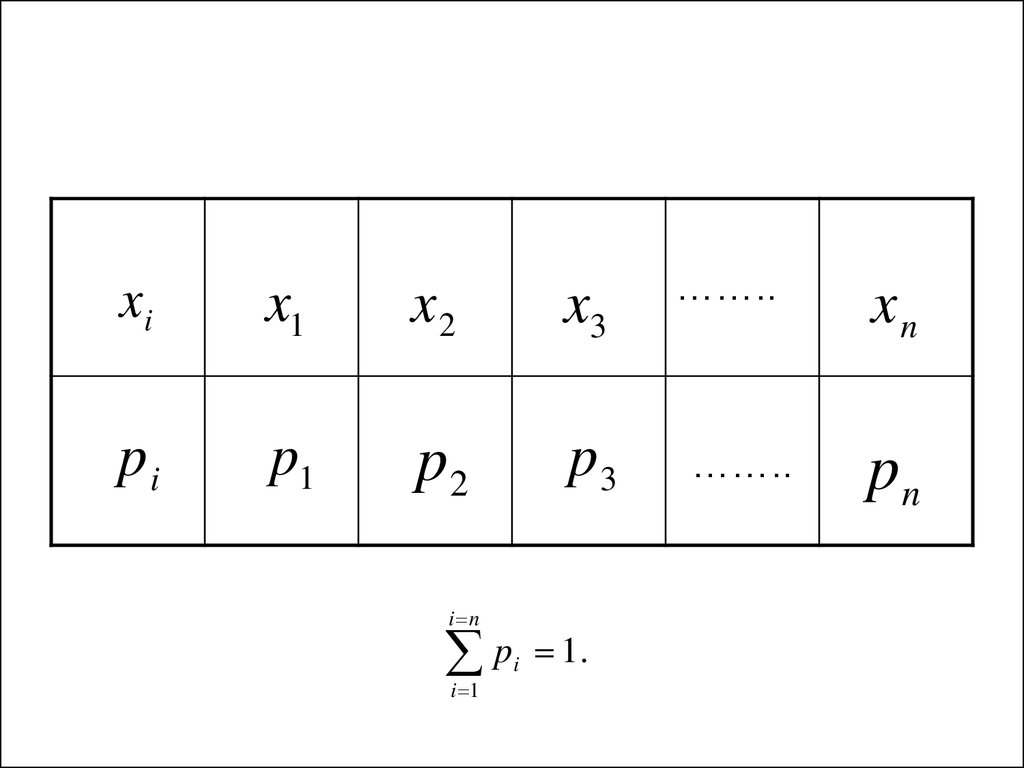
одного из них является практически
достоверным событием.
19.
7. Несколько событий образуютполную группу, если они являются
единственно возможными и
несовместными исходами испытания.
Это означает, что в результате
испытания обязательно должно
произойти одно и только одно из этих
событий.
20. «Статистическое определение» вероятности случайного события
21.
• Опр. Пусть при n - кратном повторенииопыта G событие A произошло m A
раз. Частотой n (A) события A
называется отношение
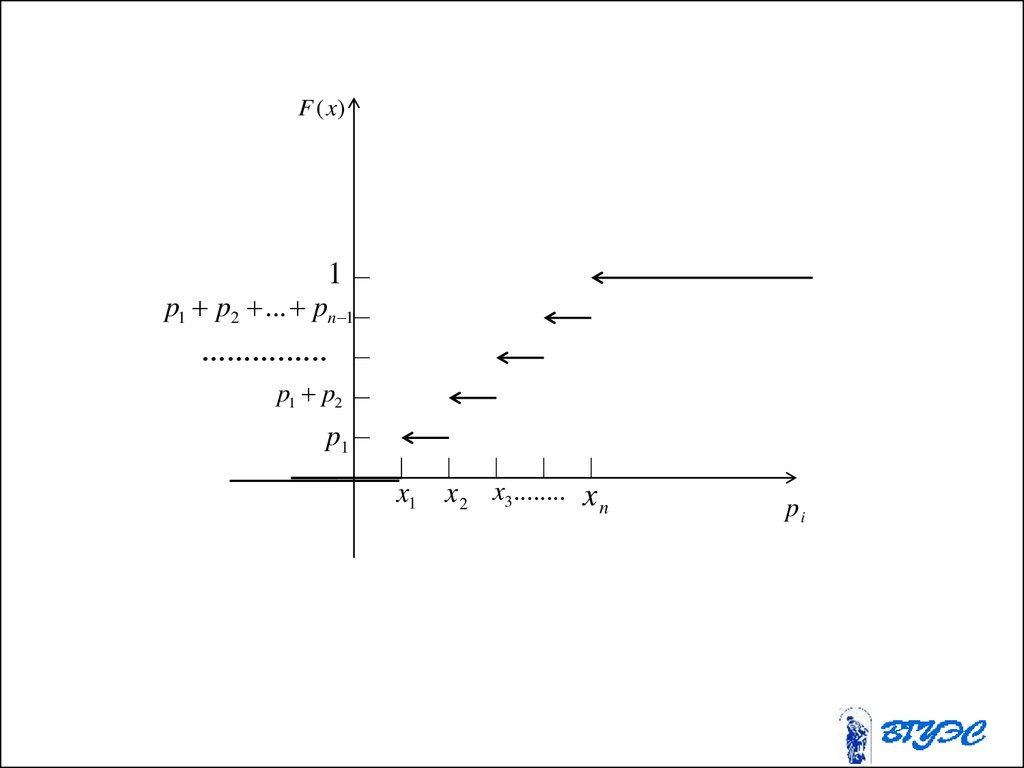
mA
n ( A)
n
22.
Опр.Вероятность случайного события – это
связанное с данным событием постоянное
число, около которого колеблется частота
наступления этого события в длинных
сериях опытов.
23.
0 n A 10 P A 1
• Если событие A - достоверное, то
P A 1.
• Если событие A - невозможное, то
P A 0.
24. Комбинация событий
25.
• Опр. Суммой событий A и B называетсясобытие A + B
, состоящее в том, что в
опыте произойдет хотя бы одно из этих
событий A или B .
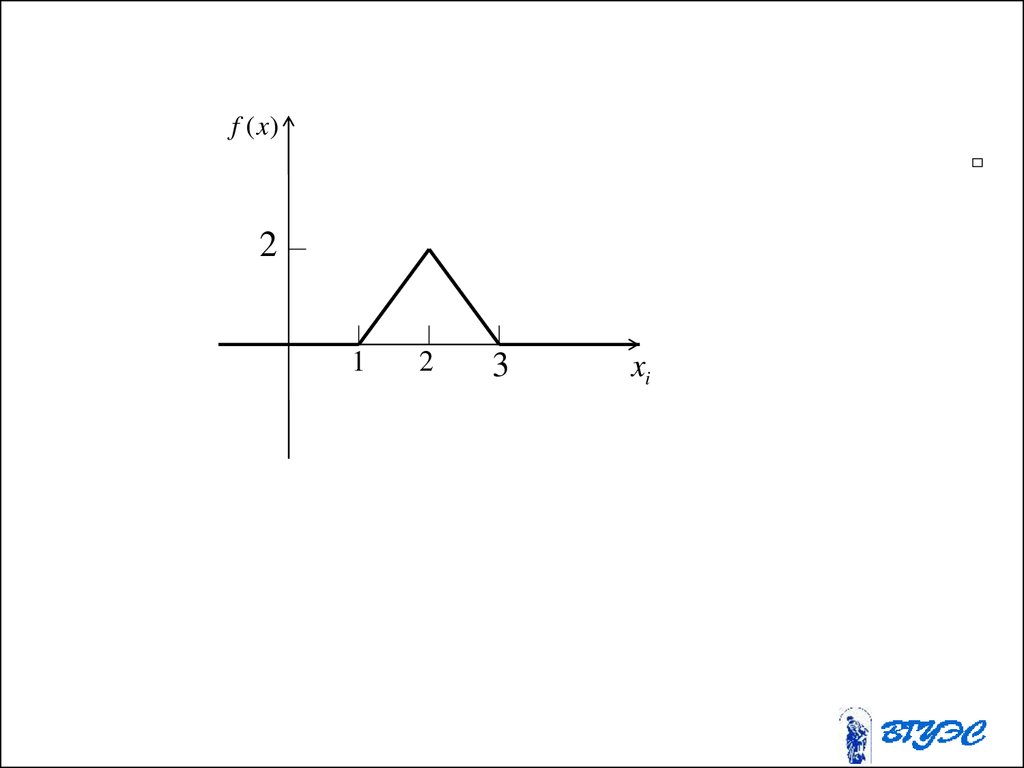
26.
A BA
B
27.
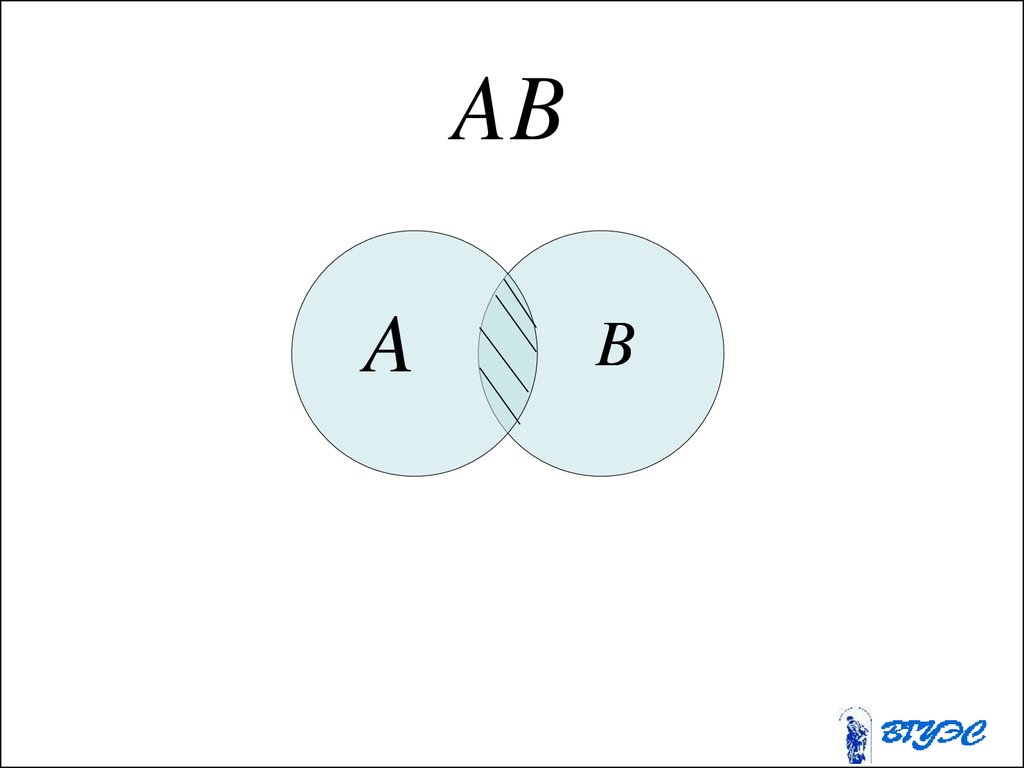
• Опр. Произведением событий A и Bназывается событие AB , состоящее в
одновременном появлении этих
событий.
28.
ABA
B
29.
• Опр. Событие А называетсяпротивоположным событию A , если
оно считается наступившим тогда и
только тогда, когда A не наступает.
30.
АA
31.
Опр. Разностью A B двух событийA и B называется событие, которое
состоится, если событие A произойдет, а
событие B не произойдет.
32.
A BA
B
33. Правило сложения вероятностей.
34.
Если события несовместны, товероятность их суммы равна сумме
вероятностей этих событий:
P A B P A P B
35.
• Следствие.P A P A 1
36.
P A B P A P B P(AB)37. Классический способ подсчета вероятности
38.
• Эту формулу применяют в тех случаях,когда исходы некоторого испытания
образуют полную группу событий и
равновозможны.
• Такие исходы называются элементарными
исходами
39.
kP A
n
40.
• Вероятность события равна отношениючисла элементарных исходов,
благоприятных для этого события, к
общему числу элементарных исходов.
41. Геометрическое определение вероятности
42.
Опр. Геометрической вероятностьюсобытия A называется отношение меры
области благоприятствующей появлению
события A , к мере всей области
mes g
P A
mes G
43. Условная вероятность
44.
• Опр. Условной вероятностью PB Aсобытия A относительно события B
называется вероятность осуществления
события A при условии, что событие B
уже произошло.
45.
P ABPB A
P B
P AB P B PB A
46.
• Пример. Слово “лотос” составлено изодинаковых букв- кубиков. Кубики
рассыпаны. Берут наугад один за
другим три кубика. Какова вероятность
того, что при этом появиться слово
“сто”.
• Решение: A - проявиться слово «сто»
A1 - первой извлечена “с”
A2 - второй извлечена “т”
A3 - третьей извлечена “о”
47.
• Представим событие A в виде:A A1 A2 A3
48.
Тогда:1 1 2
P A P A1 PA A2 PA A A3
5 4 3
1
1 2
49. Независимые события
50.
• Опр. События называютсянезависимыми, если наступление одного
не меняет шансов появления другого .
Если события
A
и
B
независимы, то
P AB P A P B
51. ЗАМЕЧАНИЯ.
• Для совместных событий:P( А В) P( А) P( В) P( АВ);
• Для несовместных событий:
P( А В) P( А) P( В);
• Для независимых событий:
P( AB) P( A) P( B);
• Для зависимых событий:
P AB P A PA B
52. ФОРМУЛА ПОЛНОЙ ВЕРОЯТНОСТИ
53.
• Предположим, что событие A может наступитьтолько вместе с одним из нескольких попарно
несовместных событий
Н1 ,..., Н n
тогда имеет место формула
n
P( А) P( H i ) PH ( A)
i 1
i
54. ФОРМУЛА БАЙЕСА
55.
• Эта формуларешает следующую
задачу: пусть произведен опыт, и в
результате него наступило событие A.
Сам по себе этот факт ещё не позволяет
сказать, какое из событий Н1 ,..., Н n имело
место в проделанном опыте. Можно
поставить следующую задачу: найти
вероятности PA H i
56.
PA H iP H i PH A
P A
i
57. Формула Бернулли
58.
P( A) Pn ( k ) C p qk
n
k
n k
• где n- столько раз проводили опыт;
k - число появления соб. A ;
p - вероятность появления соб. A ;
q - вероятность не появления соб. A,
( q 1 p).
59.
Замечание.• Формулу Бернулли используют при
n 10
60.
n 1(q p) q C q p
n
C q
2
n
n 2
n
1
n
n 1
n
n 1
p ... C q p p
2
n
61.
т.к. p q 1 и Pn ( k ) Cnk p k , q n kто эту формулу можно переписать в виде
Pn (0) Pn (1) Pn (2) ... Pn (n 1) Pn (n) 1
62.
• СобытиеA произойдет:
• а) менее
k
раз
Pn (0) Pn (1) Pn (2) ... Pn (k 1);
• б) не менее
k
раз
Pn (k ) Pn (k 1) ... Pn (n 1) Pn (n);
63.
• в) болееk
раз
Pn (k 1) Pn (k 2) ... Pn (n 1) Pn (n);
• г) не более
k
раз
Pn (0) Pn (1) Pn (2) ... Pn (k 1) Pn (k );
64. Наиболее вероятное число успехов
65.
• РассмотримPn (0), Pn (1), Pn (2),...., Pn (n)
Pn (k ) Pn (k 1)
k 1 q
1
n k p
( k 1) q (n k ) p
k np q
66.
илиPn (k ) Pn (k 1)
k 1 q
1
n k p
(k 1) q (n k ) p
k np q
np q k0 np p
67. Вероятность при больших значениях
ВероятностьPn (k )
при больших значениях
n
68. Локальная приближенная формула Лапласа ( -велико)
Локальная приближеннаяформула Лапласа
( n -велико)
69.
Pn (k )где
x
1
npq
( x),
k np
npq
;
70.
( x)1
e
2
x2
2
;
( x) ( x)
71. Интегральная формула Лапласа
72.
• Формула позволяет найтиk k2
P (k ) P (k
k k1
n
n
1
k k2 )
x2
0
x2
x1
x1
0
Pn (k1 k k2 ) ( x )dx ( x )dx ( x )dx
x1
x2
0
0
( x)dx ( x)dx.
73.
• Пустьx
x
t2
2
1
( x ) (t )dt
e dt;
2
0
0
( x ) ( x )
74.
Свойства интегральной функцииЛапласа
1)
( x ) ( x )
2) при
x x 0,5
75.
• ТогдаPn (k1 k k2 ) ( x1 ) ( x2 ),
где
x1
k1 np
npq
, x2
k 2 np
npq
.
76.
• Формулы применяются приnpq 9,
но при npq 20 дают
незначительную погрешность при
выполнении условия
77. Вероятность того, что частота наступления соб. в опытах отклонится от вероятности соб. не более чем на :
Вероятность того, что частотанаступления соб. A в n опытах
отклонится от вероятности
соб. A не более чем на :
mA
P
p 2
n
n
pq
78. Приближенная формула Пуассона
79.
n велико,
p 0,1
np 10
Pn (k )
k
k!
e
80.
• Док-во: Воспользуемся формулой БернуллиPn (k ) C p q
k
n
т.к.
np
, то
p
k
n
n k
,
81.
n!Pn k
1
k! n k ! n
n
k
n k ! n k 1 ... n 1 n
Pn k
k! n k !
n
k
n k
1
n
n k
82.
n n 1 n (k 1)Pn (k )
...
n n
n
k!
k
при
n
Pn (k )
k
k!
e
1
n
n
1
n
k
83.
• Формулу Пуассона можно использоватьесли n велико, p 0,1
np 10
84. Случайные величины
85.
• Опр. Случайной называетсявеличина, которая в результате
опыта может принять то или
иное
возможное
значение,
неизвестное
заранее,
но
обязательно одно.
86.
• Опр. Дискретной случайнойвеличиной называют такую
случайную величину, множество
возможных значений которой
либо конечно, либо бесконечно,
но обязательно счетно.
87.
• Опр. Непрерывной случайнойвеличиной называют такую
случайную величину, которая
может принять любое значение
из некоторого конечного или
бесконечного интервала.
88.
• Случайные величины:• значения:
x, y, z,.... .
X ,Y , Z ,....;
89. Операции над случайными величинами.
90.
X : x1 , x2 ,..., xi ,..., xn ;Y : y1 , y2 ,..., y j ,..., ym .
91.
Определение.• Суммой X Y случайных
величин X и Y
называется случайная
величина Z , возможные
значения которой есть
92.
x1 y1 , x1 y2 , x1 y3 ,..., x1 y j ,x2 y1 , x2 y2 ,..., x2 y j ,...,
xi y1 ,
xi y 2 ,
xi y3 ,...,
xi y j ,..., xn y m .
93.
• Опр. Произведением X Yслучайных величин X и Y
называется случайная
величина Z , возможные
значения которой есть
94.
x1 y1 , x1 y 2 , ..., x1 y j ,x2 y1 , x2 y2 ,...,
x2 y j ,..
..., xi y1 , xi y2 ,..., xi y j ,..
..., xn ym .
95.
• Опр. Произведением C Xслучайной величины X на C
постоянную называется случайная
величина Z , возможные значения
которой есть
Cx1 , Cx2 , Cx3 ,..., Cxi .
96. Закон распределения случайной величины
97.
• Опр. Законом распределениядискретной случайной величины
называется всякое соотношение,
устанавливающее связь между
возможными значениями
случайной величины и
соответствующими вероятностями.
98.
• Закон распределенияслучайной величины можно
задать, как и функцию:
табличным, графическим и
аналитическим способами.
99.
• Опр. Две случайные величиныназываются независимыми,
если закон распределения
вероятностей одной из них не
зависит от того какие
возможные значения приняла
другая.
100. Табличный способ
101. Ряд распределения случайной величины
102.
• ПустьX x1 тогда
P( X x1 ) p1 ;
X x2 тогда P( X x2 ) p2 ;
X x3 тогда
P( X x3 ) p3 ;
…………………………………
X xn тогда
P ( X x n ) p n.
103.
np
i 1
i
1.
104.
xix1
x2
x3
pi
p1
p2
p3
n
p
i 1
i
1.
……
xn
……
pn
105. Графический способ
106. Многоугольник распределения
107.
xi1
2
3
4
5
pi
0,1
0,3
0,2
0,3
0,1
pi
0,3
0,2
0,1
1
2
3
4
5
xi
108. Аналитический способ
109. Функция распределения вероятностей
110.
• Опр. Функцией распределениявероятностей случайной величины X
называется функция F (x) , задающая
вероятность того, что случайная
величина X принимает значение,
меньшее x , т.е.
.
F ( x) P( X x)
111. Свойства функции распределения.
112.
• 1. 0 F ( x) 1 ;Т.к F ( x) P( X x) , а 0 p 1.
• 2. F (x) - неубывающая функция и для
P( X ) F ( ) F ( );
A:
X ;
B:
X ;
C:
X .
B A C
113.
P( A) P( X ) F ( );P( B) P( X ) F ( );
P(C ) P( X ).
114.
P( B) P( A) P(C ),F ( ) F ( ) P( X ),
P( X ) F ( ) F ( ),
115.
• Т.к.P( X ) 0 F ( ) F ( ) 0,
F ( ) F ( ).
Отсюда
F (x) - неубывающая.
116.
3. Если F (x ) - функция распределения,lim F x 1
то lim F x 0
x
x
4.Если X - непрерывная случайная
величина, то
.
P( X ) 0
P( X ) P( X )
P( X ) P( X ).
117.
• Если X - дискретная случайная величина,F ( x)
то
P( X x ).
i
xi x
xi
x1
x2
x3
pi
p1
p2
p3
i n
p
i 1
i
1.
……..
……..
xn
pn
118.
x x1 ,F ( x) P( X x1 ) 0;
x1 x x2 ,
x2 x x3 ,
F ( x) P( X x2 ) P( X x1 ) p1;
F ( x) P( X x3 ) P( X x1 ) P( X x2 ) p1 p2 ;
…………………………………………...........
xn 1 x xn , F ( x) P( X xn ) P( X x1 ) P( X x2 ) ... P( X xn 1 )
p1 p2 ... pn 1;
x xn ,
F ( x) P( X xn ) p1 p2 ... pn 1.
119.
x x1 ;0,
p ,
;
x
x
x
2
1
1
p1 p2 ,
x2 x x3 ;
F ( x)
..........
..........
p1 p2 ... pn 1 , xn 1 x xn ;
1,
x xn .
120.
F (x)1
p1 p2 ... pn 1
...............
p1 p2
p1
x1 x 2 x3 ........ x n
pi
121. Плотность распределения вероятностей
122.
• Пусть X -непрерывная случайнаявеличина.
Рассмотрим вероятность попадания
значений случайной величины в
элементарный участок ( x; x x) :
P( x X x x) F ( x x) F ( x),
P( x X x x) F ( x x) F ( x)
,
x
x
123.
P( x X x x)F ( x x) F ( x)
lim
F ( x).
lim
x
x
x 0
x 0
Обозначим
F ( x) f ( x).
124.
• Опр. Дифференциальной функциейраспределения или плотностью
распределения вероятностей наз.
первая производная интегральной
функции распределения F (x ).
125.
• График дифференциальной функциираспределения f (x) наз. кривой
распределения:
f (x)
x
126. Свойства плотности распределения вероятности.
127.
• 1.Для x f ( x) 0.• 2.Для f (x) имеет место равенство
P( X ) f ( x)dx.
• 3.
f ( x)dx 1.
x
• 4.
F ( x)
f (t )dt
128. Числовые характеристики случайных величин.
129. Математическое ожидание.
130.
xix1
x2
x3
pi
p1
p2
p3
i n
p
i 1
i
1.
……..
……..
xn
pn
131.
• Опр. Математическим ожиданием MXдискретной случайной величины X наз.
сумма произведений всех возможных
значений случайной величины на
соответствующие вероятности появления
этих значений:
n
MX xi pi .
i 1
132.
• Пусть случайная величина X принялазначения
x1 , x2 ,..., xk .
Причем x1 появилось m1 раз,
x 2 появилось m2 раз,
……………………….,
x k появилось m k раз.
x1 m1 x2 m2 ... xk mk
mk
m1
m2
X
x1 x2 ... xk ,
m1 m2 ... mk
n
n
n
где
m1 m2 ... mk n.
133.
• При n• Тогда
mi
pi .
n
X MX
.
134.
• Опр. Математическим ожиданиемнепрерывной случайной величины X ,
возможные значения которой
принадлежат a; b , называется
b
f ( x)dx.
a
• Если возможные значения принадлежат
;
, то
MX
f ( x)dx.
135. Свойства математического ожидания
136.
1. MC C.2. M (CX ) C MC .
3.Если X , Y независимые случайные
величины, то
M ( X Y ) MX MY .
4.Если X , Y независимые случайные
величины, то
M ( XY ) MX MY .
5. M ( X MX ) 0.
137.
• Пример 1.xi
2
5
8
19
p i 0,2 0,3 0,4 0,1
MX 2 0,2 5 0,3 8 0,4 19 0,1 7.
138. Пример 2.
0 ,x 1,
f ( x)
x 3,
0,
x 1;
1 x 2;
2 x 3;
x 3.
139.
MX x f ( x)dx1
2
3
2
1
2
3
1
x 0dx x ( x 1)dx x (3 x)dx x 0dx ( x 2 x)dx
3
(3x x 2 )dx
2
2
x x
3 2 1
3
2
2
3x x
2.
3 2
2
2
3
140.
f (x )2
1
2
3
xi
141. Дисперсия
• Опр. Математическое ожиданиеквадрата отклонения СВ X от её
математического ожидания MX
называют дисперсией СВ X :
DX M ( X MX ) .
2
142.
• Если СВX
- дискретная СВ, то
n
DX ( xi MX ) pi .
2
i 1
• Если СВ
X
- дискретная СВ, то
DX ( x MX ) f ( x)dx.
2
143.
• Среднее квадратическое отклонение( x) DX .
144. Свойства дисперсии
1.
2.
3.
4.
5.
D( X Y ) DX DY .
DC 0.
D(CX ) C DX .
2
DX MX (MX ) .
2
2
D( X MX ) DX .
145.
• Опр. СВ X MX называетсяцентрированной:
M ( X MX ) 0, D( X MX ) DX .
Опр. СВ
X MX
x
называется стандартной:
X MX
X MX
0, D
1.
M
x
x
146.
• Опр. Начальным моментом k гопорядка k СВ X называется
k MX .
k
k
MX :
• Опр. Центральным моментом k
порядка k СВ X называется
го
M ( X MX ) : k M ( X MX ) .
k
k
147.
• Опр. Коэффициентом асимметрииназ-ся величина : 3
3
x
.
3
A 3.
x
A
148.
• Опр. Эксцессом4
3.
4
x
E
наз-ся величина
4
E 4 3.
x
149. Виды распределения
150. Равномерное распределение
151.
0,1
f ( x) ,
a
b
0,
x a;
a x b;
x b.
152.
f (x)1
b a
a
b a
MX
,
2
b
x
(b a)
DX
,
12
2
A 0, E 0.
153. Нормальное распределение
154.
f ( x)1
2
e
( x a )
2
2
2
.
155.
MX a,• Если СВ
X~
DX ,
2
A 0,
E 0.
N ( a, ) , то
a a
P( X ) Ф
Ф
.
156.
• Если СВX
~
N ( a, ) , то
P ( X a ) 2 Ф
.
157.
• Обозначимz
, тогда
P( X a z) 2 Ф z .
158.
• Пустьz 1,
P( X a ) 2Ф(1) 0,6437;
z 2,
P( X a 2 ) 2Ф(2) 0,9545;
z 3,
P( X a 3 ) 2Ф(3) 0,9973.
159.
• Правило «трёх сигм»: если СВ Xраспределена по нормальному закону, то
отклонение этой величины от её MX по
абсолютной величине практически не
превышает утроенного среднего
квадратического отклонения.
• Если СВ X ~ N (0;1) , т.е.
СВ X - стандартная, то
P( X ) 2 Ф .
160. Биномиальное распределение
161.
xipi
x1
x2
…………
xn
p1
p2
…………
pn
i n
p
i 1
pi Pn (k ) C p q
k
n
MX np,
k
i
n k
1.
,
DX npq.
162. Распределение Пуассона
163.
xipi
x1
x2
…………
xn
p1
p2
…………
pn
i n
p
i 1
pi Pn (k )
MX ,
k
k!
e ,
DX .
i
1.
164. Закон больших чисел
165. Неравенство Чебышева
166.
• Пусть имеется СВ X с математическиможиданием
и дисперсией
m .
Каково бы ни было
D положительное
число , вероятность того, что
величина отклонится от своего
математического ожидания не меньше
чем на
, ограничена сверху числом
D
:
2
P X m
D
2
167.
• Если СВ X , для которой существуетматематическое ожидание m , может
принимать только неотрицательные
значения(т.е. P X 0 0 ), то вероятность
того, что принятое ею значение окажется
не меньше 1, не превосходит числа m :
P X 1 m.
168.
• Следствие P X m 1D
2
.
P X m P X m 1,
P X m 1 P X m
P X m 1
D
2
.
D
2
,
169. Теорема Чебышева
170.
• Пусть имеется бесконечнаяпоследовательность независимых
случайных величин X 1 , X 2 ,..., X n с одним и
тем же математическим ожиданием и
дисперсиями, ограниченными одной и той же
M X 1 M X 2 ... M X n m,
постоянной:
D X 1 C, D X 2 C, ...., D X n C.
• Тогда каково бы ни было положительное
число ,
X 1 X 2 ... X n
P
m 1, при n .
n


























































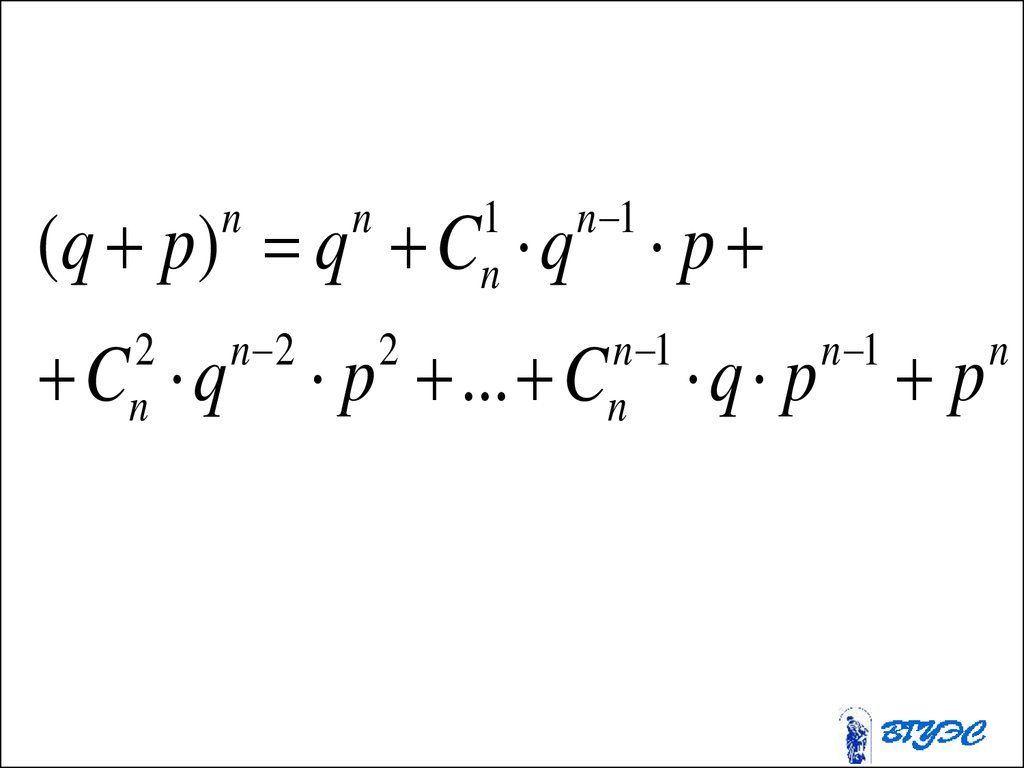





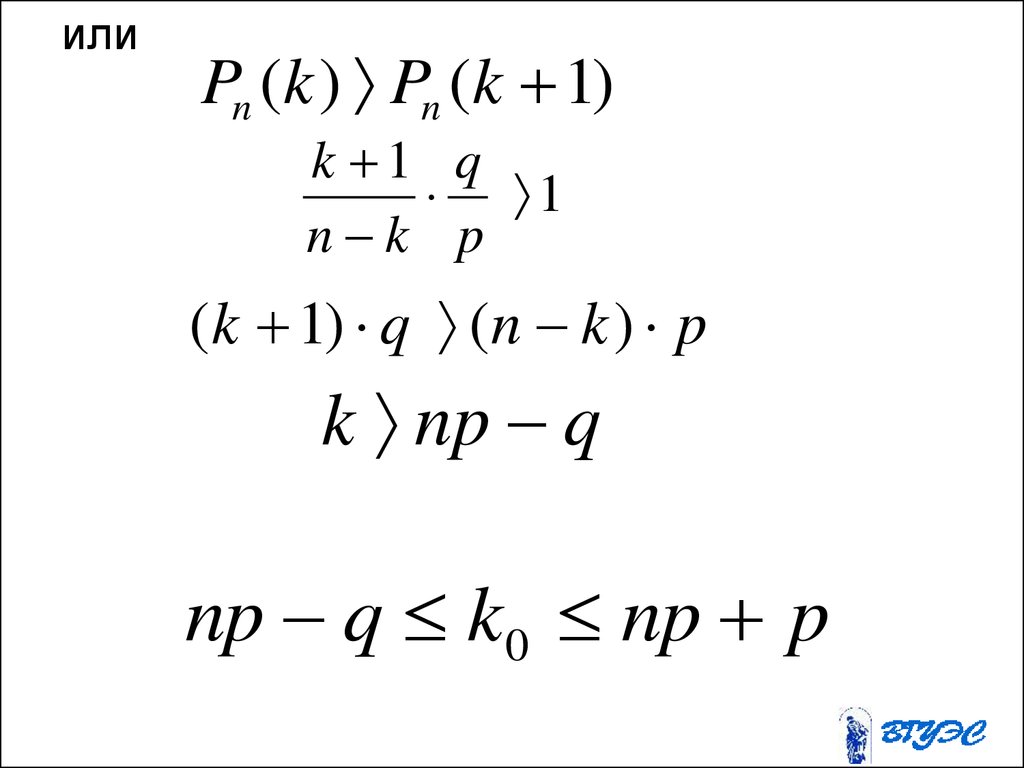



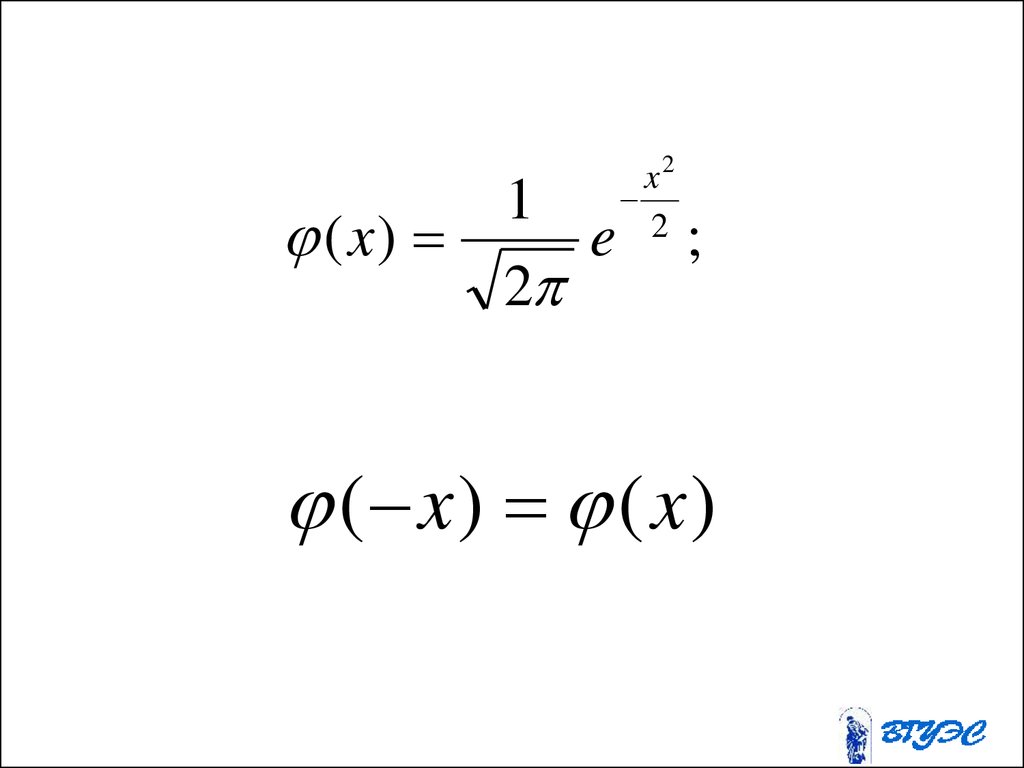


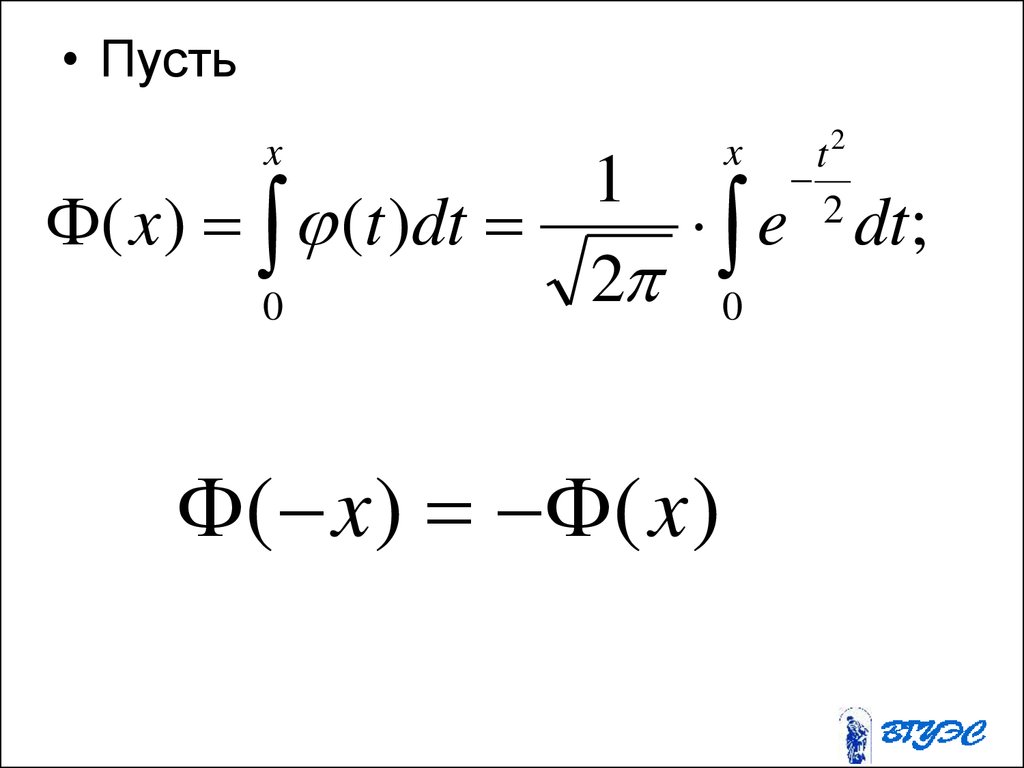
















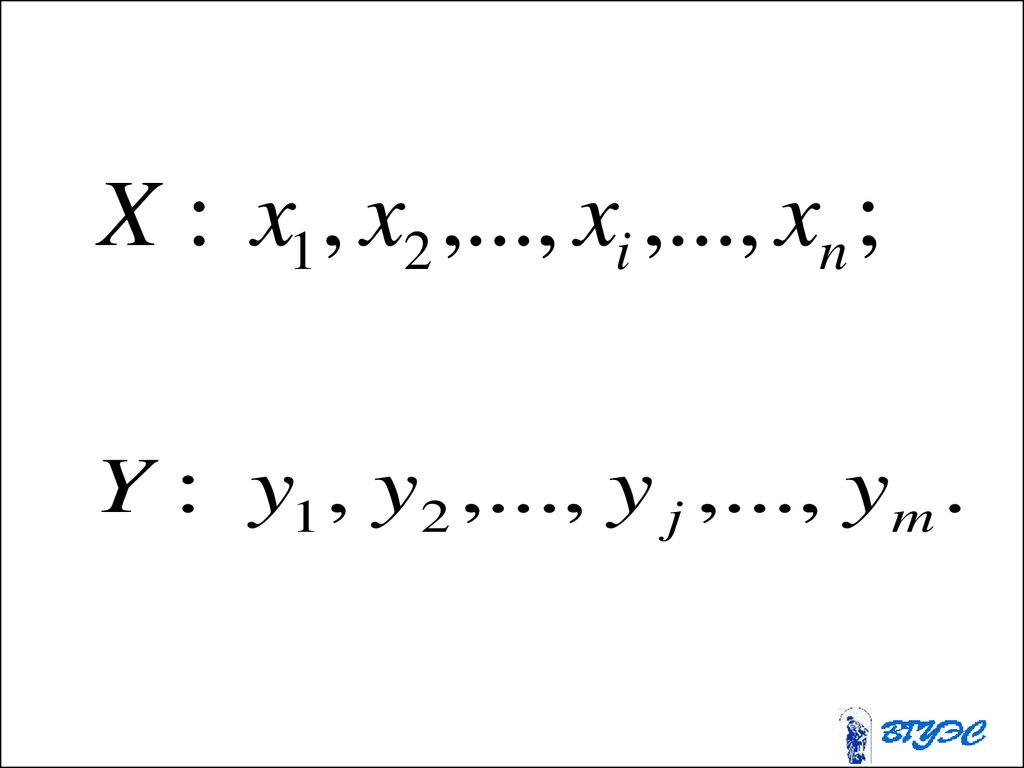

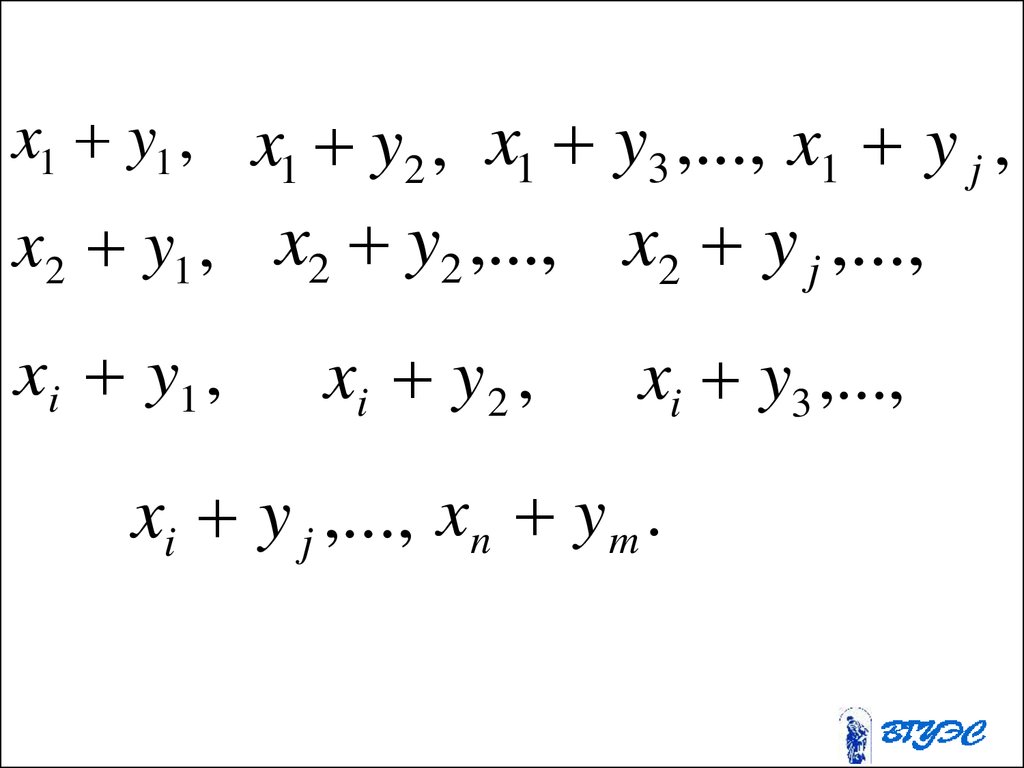

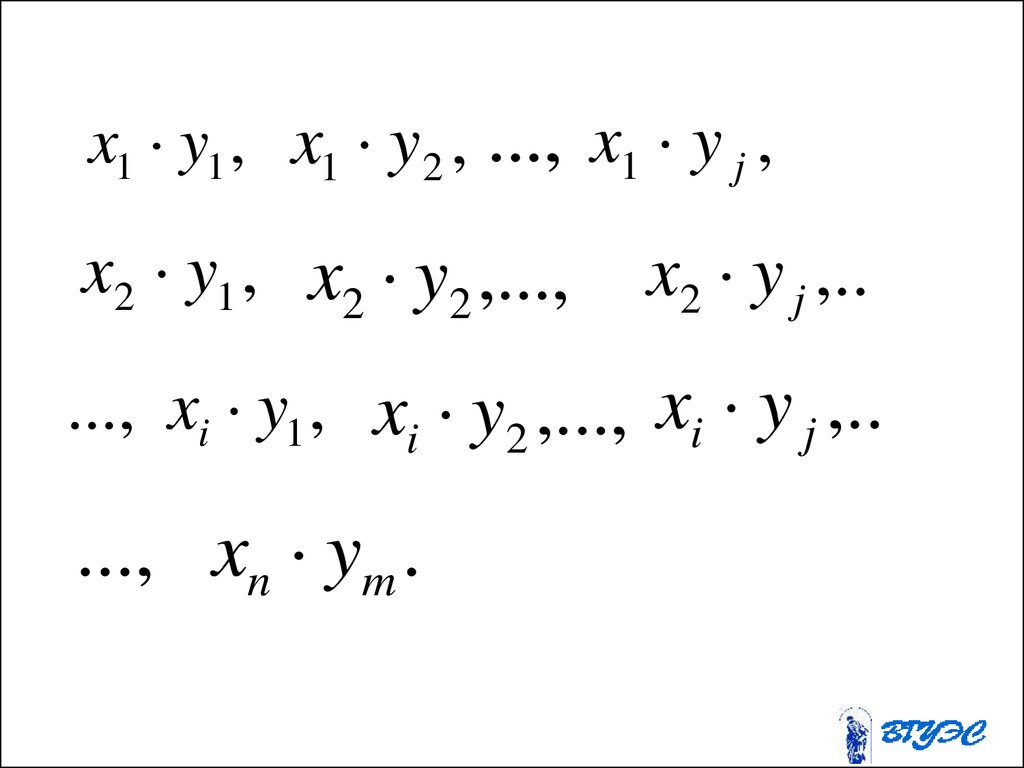


















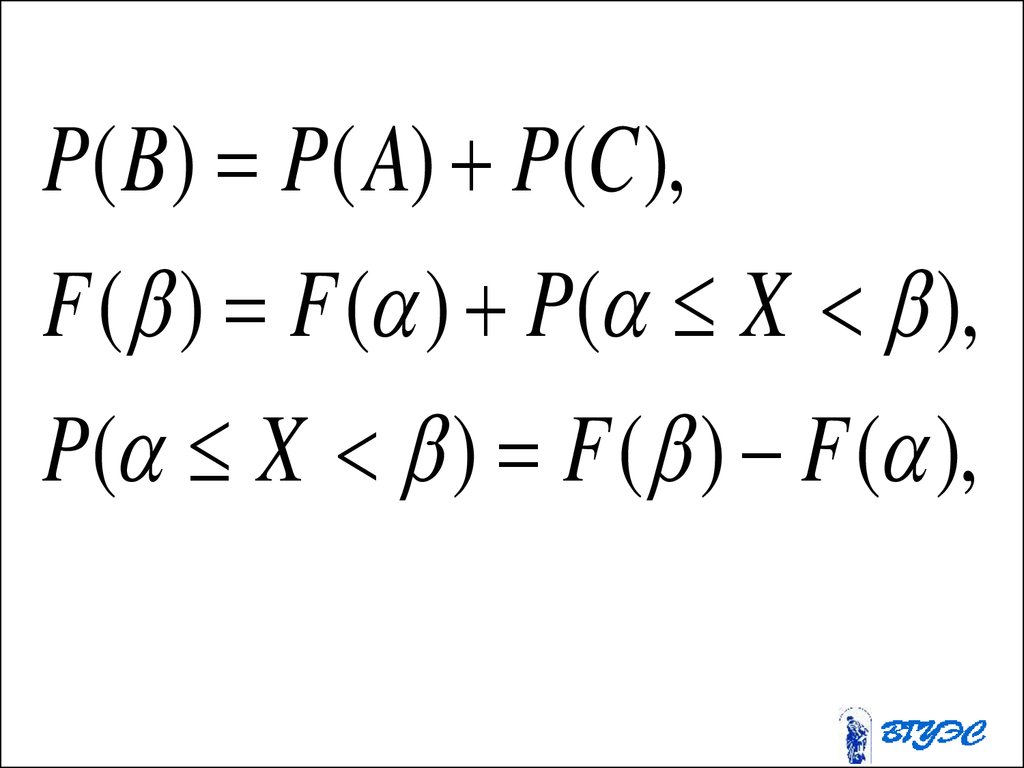
















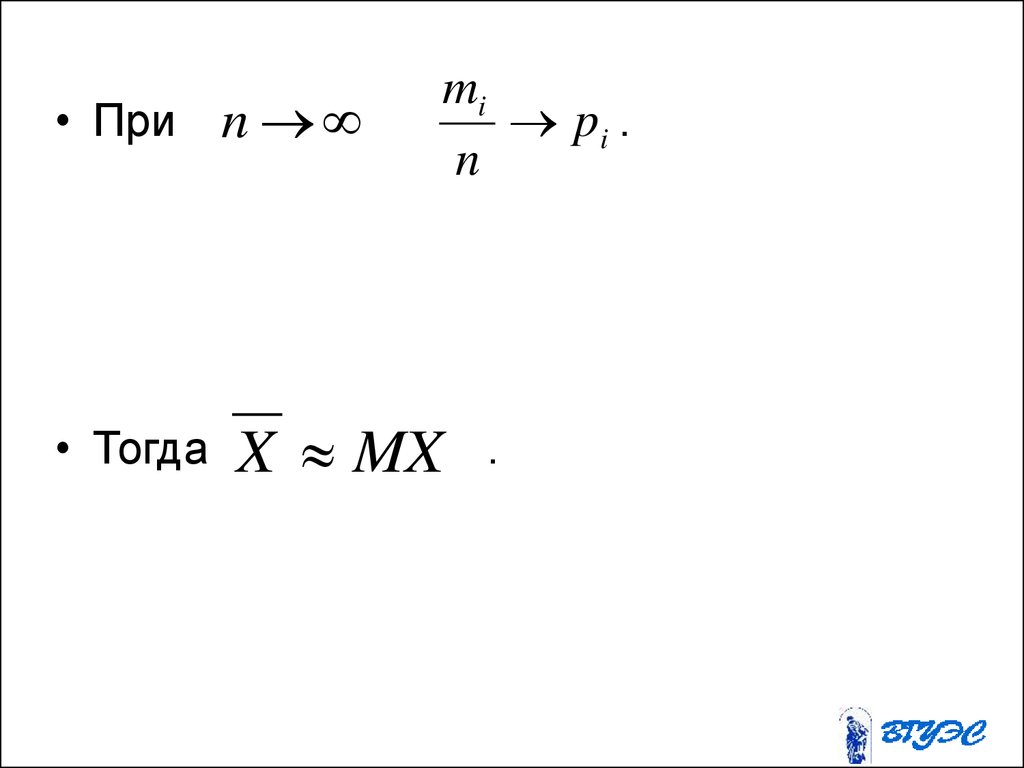



















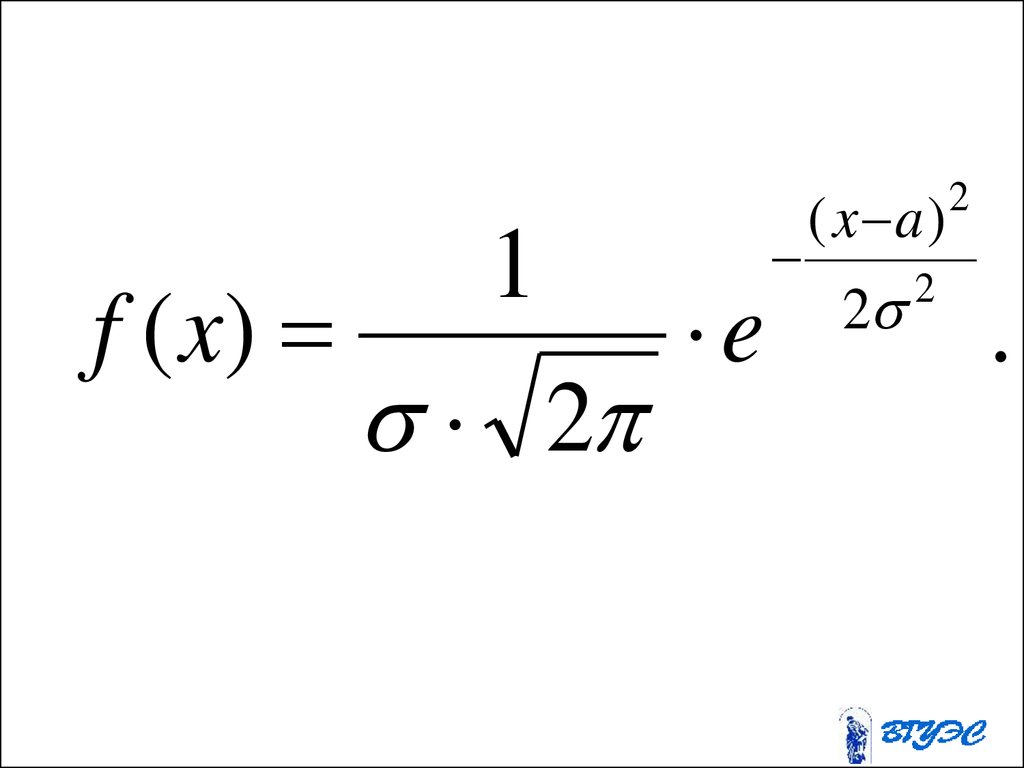
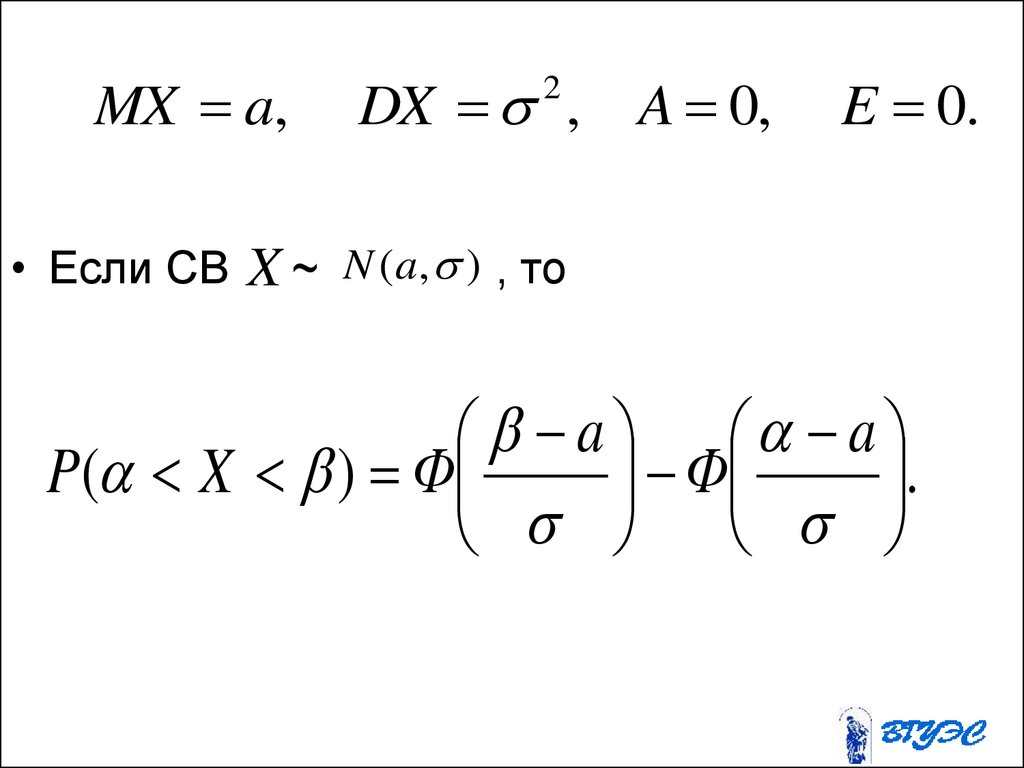

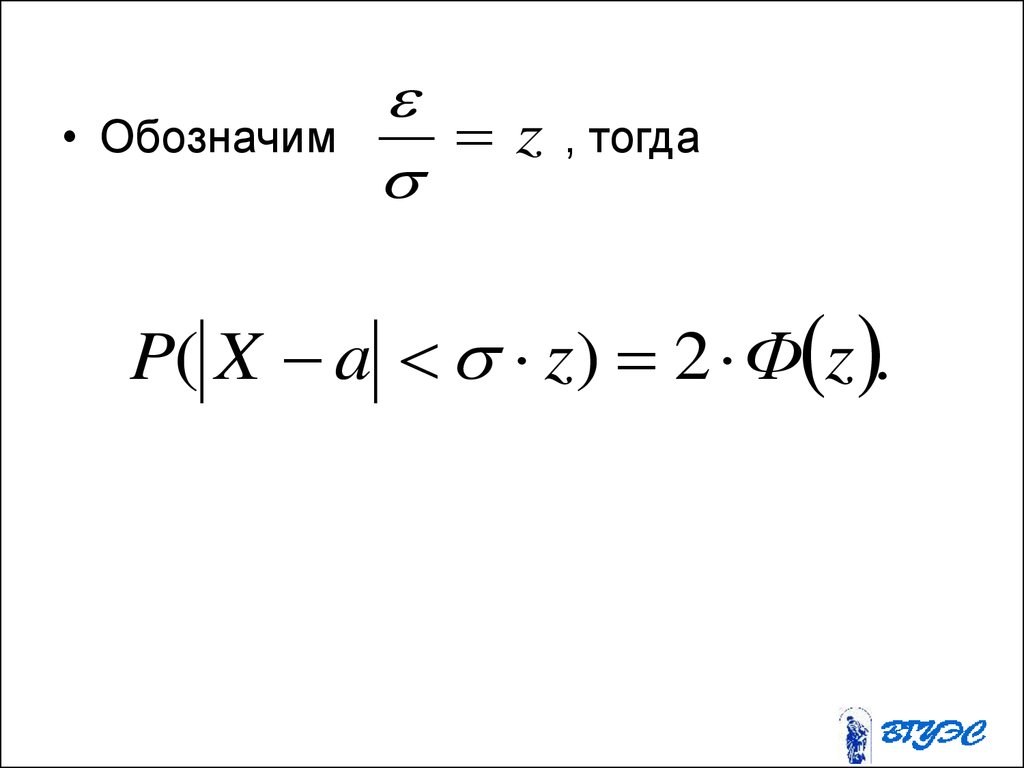
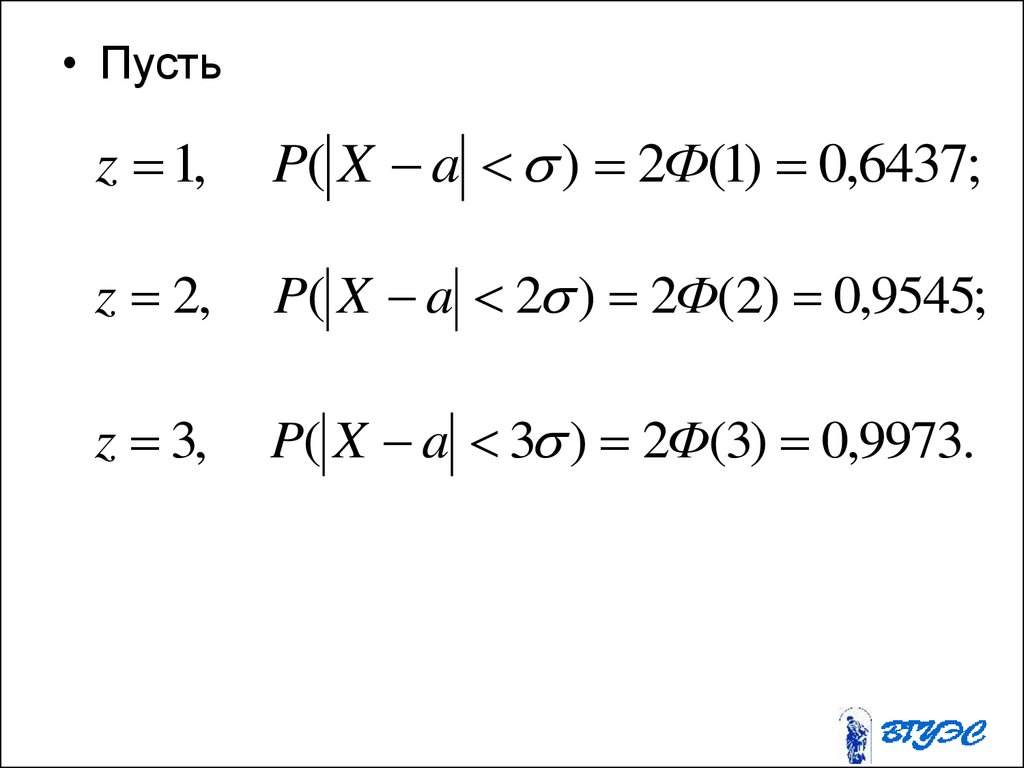












 mathematics
mathematics








