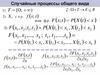Similar presentations:
Стационарные случайные процессы. Лекция 2
1. Стационарные случайные процессы
1. Определение стационарнойслучайной функции.
2. Эргодическое свойство
стационарных случайных величин.
3. Некоторые типы случайных
процессов.
1
2. Определение стационарной случайной функции 1.1. Определение и свойства стационарной случайной функции
1.Определение стационарной случайной функции
1.1. Определение и свойства стационарной случайной
функции
Среди случайных функций целесообразно выделить класс функций,
математические ожидания которых сохраняют одно и то же
постоянное значение при всех значениях аргумента t и
корреляционные функции которых зависят только от разности
аргументов t2 - t1.
Такие случайные функции называют «стационарными в широком
смысле» в отличие от случайных функций, «стационарных в
узком смысле» (все характеристики этих функций не зависят от
самих значений аргументов, но зависят от их взаимного
расположения на оси t).
Из стационарности в узком смысле следует стационарность в
широком смысле; обратное утверждение неверно.
В рамках корреляционной теорией, которая использует только две характеристики
(математическое ожидание и корреляционную функцию), далее рассмотрим
случайные функции, стационарные в широком смысле, причем будем их
называть просто стационарными.
2
3.
Определение 1.1. Стационарной называютслучайную функцию X(t), математическое ожидание
которой постоянно при всех значениях аргумента t
и корреляционная функция которой зависит только
от разности аргументов t2–t1. Из этого определения
следует, что:
1) корреляционная функция стационарной случайной
функции есть функция одного аргумента = t2 - t1,
т.е.
Kx(t1, t2) = kx(t2 - t1) = k( );
(1)
2) дисперсия стационарной случайной функции
постоянна при всех значениях аргумента t и равна
значению ее корреляционной функции в начале
координат ( = 0), т. е.
Dx(t)=Kx(t,t) = kx(t - t) = kx(0)
(2)
3
4. Свойства корреляционной функции стационарной случайной функции
Свойство 1. Корреляционная функция стационарнойслучайной функции есть четная функция:
kx( ) = kx(- )
Доказательство. Корреляционная функция любой
случайной функции при перестановке аргументов не
изменяется. В частности, для стационарной функции
kx(t2 - t1) = kx(t1 - t2).
Положив = t2 - t1, получим kx( ) = kx(- ).
Свойство 2. Абсолютная величина корреляционной функции
стационарной случайной функции не превышает ее
значения в начале координат:
| k x ( ) | k x (0).
4
5. 1.2. Нормированная корреляционная функция стационарной случайной функции
Кроме корреляционной функции для оценки степенизависимости сечений стационарной случайной функции
используют еще одну характеристику - нормированную
корреляционную функцию.
Ранее нормированная корреляционная функция была
определена
K x (t1 , t2 )
x (t1 , t2 )
x (t1 ) x (t2 )
(3)
В частности, для стационарной функции числитель и
знаменатель этой дроби имеют вид (см. (1), (2))
K x (t1 , t2 ) k x ( ), (t ) Dx (t ) k x (0) .
Следовательно, для стационарной функции правая часть (3)
равна k x ( ) / k x (0) и является функцией одного аргумента ;
очевидно, и левая часть (3) - функция от .
5
6.
Определение 1.2. Нормированной корреляционной функциейстационарной случайной функции называют неслучайную
функцию аргумента : x ( ) k x ( ) / k x (0)
Абсолютная величина нормированной корреляционной
функции стационарной случайной функции не превышает
единицы.
Определение 1.3. Стационарно связанными называют две
случайные функции X(t) и Y(t), если их взаимная
корреляционная функция зависит только от разности
аргументов = t2 - t1.
Rxy (t1 , t 2 ) rxy ( ).
Взаимная корреляционная функция стационарно
связанных случайных функций обладает следующим
свойством:
rxy ( ) rxy ( ).
Определение 1.4. Стационарными и стационарно
связанными называют две стационарные случайные
функции X(t) и Y(t), взаимная корреляционная функция,
которых зависит только от разности аргументов = t2 - t1.
6
7.
Теорема 1.1. Корреляционная функция производной X ' (t ) xдифференцируемой стационарной случайной функции X(t)
равна второй производной от ее корреляционной функции,
взятой со знаком минус: k ( ) k '' ( )
x
x
Теорема 1.2. Взаимная корреляционная функция
дифференцируемой стационарной случайной функции X(t)
и ее производной X ' (t ) x равна первой производной от
корреляционной функции k x ( ) , взятой со своим
(противоположным) знаком, если индекс x стоит на втором
(первом) по порядку месте:
а) r ( ) k x' ( );
б) r ( ) k x' ( );
x
xx
x
Предполагается, что = t2 - t1.
Теорема 1.3. Корреляционная функция интеграла
от стационарной случайной функции равна
t2
K y (t1 , t2 ) (t2 )k x ( )d
0
t2 t1
(t
t
Y (t ) X ( s)ds
0
t1
2
t1 )k x ( )d (t1 )k x ( )d
0
0
t
Следствие. Дисперсия интеграла Y (t ) X (s)ds от стационарной
7
случайной функции равна D (t ) 2 (t )k ( )d
t
y
0
x
0
8. 2. Эргодическое свойство стационарных случайных функций
Среди стационарных случайных функций можно выделить класс функций,оценка характеристик которых путем усреднения множества реализаций
равносильна усреднению по времени только одной реализации достаточно
большой длительности.
Определение 2.1. Стационарную случайную функцию X(t)
называют эргодической, если ее характеристики,
найденные усреднением множества реализаций,
совпадают с соответствующими характеристиками,
полученными усреднением по времени одной реализации
x(t), которая наблюдалась на интервале (0, Т) достаточно
большой длительности.
8
9.
910. 3. Некоторые типы случайных процессов. 3.1. Нормальные процессы
Определение 3.1. Случайный процессt, , t T a, b ,
называют нормальным, или гауссовым процессом, если
любые его конечномерные законы распределения
являются нормальными.
Если t , , t T , - n-мерный стационарный нормальный
случайный процесс, то его математическое ожидание постоянный n-мерный вектор, а аргументом
ковариационной функции является параметр t 2 t1.
10
11. 3.2. Процессы с независимыми приращениями
Определение 3.2. Случайный процесс t , , t T R ,называют процессом с независимыми приращениями, если
для любых N 1 и t k T , k 1, N , таких, что t1 t 2 ... t N ,
случайные величины t1 , , t 2 , t1 , ,... t N , t N 1 ,
являются независимыми.
1. Если n-мерные случайные векторы
t1 , , t2 , t1 , ,... t N , t N 1 ,
являются, вообще говоря, зависимыми, но
некоррелированными, то n-мерный случайный процесс
называют процессом с некоррелированными
(ортогональными) приращениями.
2. Если для любых N 1 и tk T , k 1, N закон
распределения приращения tk 1 , tk , зависит лишь от
tk 1 tk , k 1, N 1 , то случайный процесс t , , t T , с
независимыми приращениями называют процессом со 11
стационарными независимыми приращениями.
12. 3.3. Винеровский процесс
Определение 3.3. Если t , , t T 0, , - n-мерныйслучайный процесс, то его называют винеровским
процессом, выходящим из нуль-вектора (0), если
выполнены три условия:
1) 0, 0;
2) для любых N>1 и tk T , k 1, N , таких, что 0 t1 t2 ... t N ,
случайные векторы t1 , , t 2 , t1 , ,..., t N , t N 1 ,
являются независимыми;
3) для любых t1 , t 2 T , таких, что 0 t1 t 2 , случайный
вектор t2 , t1 , распределен по нормальному
закону с нулевым математическим ожиданием и
I n M n R
ковариационной матрицей t1 , t 2 2 I n, где —
единичная матрица.
12
13.
Винеровский процесс - процесс броуновского движения.В 1827 г. английский ботаник Р. Броун заметил, что маленькие частицы
диаметром около микрона, погруженные в жидкость, находятся в
постоянном хаотическом движении. В 1905 г. А. Эйнштейн объяснил это
движение как результат столкновения частиц с молекулами жидкости.
Он разработал математическую модель броуновского движения и
определил число Авогадро, равное числу молекул в объеме, занятом
молем газа.
Строгий математический анализ броуновского движения дал Н. Винер в
1923 г. Эвристически броуновское движение можно объяснить
следующим образом. Рассмотрим отдельную частицу, погруженную в
жидкость, обозначив через ее координаты в момент времени t>0.
Будем считать, что в начальный момент времени t>0 она находится в
начале координат, т.е. движение частицы на любом конечном
временном интервале является результатом изменения импульса
(количества движения) вследствие практически бесконечно большого
числа независимых друг от друга соударений с молекулами жидкости.
Поэтому естественно считать, что применима центральная предельная
теорема. Кроме того, можно допустить, что:
13
14.
а) смещения частицы в ортогональных направленияхпроисходят независимо;
б) k t , k 1,2,3, распределены по нормальному закону с
нулевым математическим ожиданием и дисперсией 2 t ;
в) смещение частицы в каждом k-ом ортогональном
направлении на различных непересекающихся временных
0 t1 ... t N интервалах представляется независимыми
случайными величинами
k t1 , k t2 k t1 ,..., k t N k t N 1 ;
г) смещение частицы в каждом k-ом ортогональном
направлении на временном интервале t, t h , равное
k t h k t , имеет ту же функцию распределения, что и
смещение k h k 0 , где k 0 0.
14
15.
Отметим также, что дисперсия t D k t обладаетлюбопытным свойством: 2 t 2t , t 0,
2
где постоянную интерпретируют как коэффициент
диффузии. Действительно, согласно допущению в),
случайные величины k t и k t h k t являются
независимыми. Поэтому
2
D k t h D k t D k t h k t ,
или
t h t D k t h k t .
2
2
А так как, согласно допущению г),
D k t h k t D k h ,
то
t h t h ,
2
2
2
откуда и следует отмеченное свойство. Заметим, что этот
результат является следствием из рассмотренных свойств
15
процессов с ортогональными приращениями.
16.
Замечание 3.1. Если в определении винеровского процессаусловие 0, 0 заменить условием 0, x, где ,
x X R n то получим определение винеровского
процесса, выходящего из точки х.
Замечание 3.2. Если t, , t T , — винеровский процесс с
2
коэффициентом диффузии , то случайный процесс
t , / 2 , t T , называют стандартным винеровским
процессом. Для любых t1 , t 2 T , таких, что 0 t1 t 2 ,
случайный вектор t 2 , 2 t1 , 2 распределен по
нормальному закону с нулевым математическим
ожиданием и ковариационной матрицей t2 t1 I n .
16
17.
Следует также отметить два характерных свойствавинеровских процессов.
1. Винеровский процесс является процессом со
стационарными приращениями.
2. Если t , , t T ,— винеровский процесс и — его
коэффициент диффузии, то для любых t1 , t 2 T , таких, что
0 t1 t2 , ковариационная функция равна
K t1 , t 2 t1 2 I n ,
так как винеровский процесс является процессом с
независимыми приращениями.
Докажем, что винеровский процесс является нормальным
процессом.
Для упрощения дальнейших рассуждений ограничимся
рассмотрением скалярного винеровского процесса
t, , t T 0, , предполагая, что он является стандартным.
N
N
1
и
t
Докажем, что для любых
k k 1 T , таких, что ,
0 t1 t 2 ... t N случайный вектор
t1 , t 2 , ... t N , T
17
распределен по нормальному закону.
18.
Пусть далееt 0 0;
k t k , t k 1 , , k 1, N ;
1 2 ... N .
T
Согласно определению винеровского процесса, плотность
распределения (вероятностей) случайного вектора
является плотностью N-мерного нормального
распределения, которая в данном случае имеет вид
N
f x1 ,..., x N
k 1
2
1 / 2
t k t k 1
xk2
exp
.
2 t k t k 1
18
19.
Если ввести в рассмотрение матрицу1 0 0
1 1 0
A 0 1 1
0 0 0
0
0 M N R ,
1
0 0
0
0
1
то, согласно общей теории построения законов
распределения функций случайных величин, с учетом
очевидных равенств
A , det A 1
имеем
f y1 , y2 ,..., y N f y f Ay f y1 , y2 y1 ,..., y N y N 1 .
19
20.
Таким образом, если y0 0,то N-мерная плотностьраспределения (вероятностей)
f y1 , y 2 ,..., y N
N
k 1
N
k 1
2
1 / 2
t k t k 1
2
1 / 2
t k t k 1
y k y k 1
exp
2 t k t k 1
2
y k y k 1
exp
k 1 2 t k t k 1
N
2
является плотностью N-мерного нормального распределения,
что и требовалось доказать.
20
21.
3.4. Марковские процессыВ теоретических и прикладных исследованиях, связанных с
марковскими процессами, для их конечномерных (Nмерных) функций плотности вероятностей
f x 1 ,..., x N | t1 ,..., t N используют сокращенные обозначения
f x 1 , x 2 ,..., x N .
Определение 3.4. Пусть t , , t T R, - n-мерный
случайный процесс, конечномерные функции плотности
вероятностей которого (возможно обобщенные)
f x 1 , x 2 ,..., x N заданы для любых N 1 и t k T , k 1, N ,
t1 t 2 ... t N . Если при этом условная
таких, что
функция плотности вероятностей имеет вид
f x N | x N 1 ,..., x1 f x N | x N 1 ,
то
t , , t T , называют марковским процессом.
21
22.
3.5. Пуассоновский процессОпределение 3.5. Пуассоновским процессом с параметром
> 0 называют скалярный случайный процесс
t , , t T 0, , обладающий следующими свойствами:
1) 0, 0;
2) для любых N > 1 и , t k T , k 1, N таких, что 0 t 0 t1 ... t N
случайные величины t k , t k 1 , , k 1, N, являются
независимыми;
3) для любых t1 , t 2 T, таких, что 0 t1 t 2 ,случайная
величина t 2 , t1 , распределена по закону
Пуассона с параметром t 2 t1 ,
т.е.
t 2 t1
P t 2 , t1 , k
k
k!
e t 2 t1 , k N 0 .
Пуассоновский процесс играет важную роль в различных
приложениях теории случайных процессов, в частности, в
22
теории массового обслуживания.






















 mathematics
mathematics