3сем_Лк 9_Числ.ряды_Признаки сходим

1.

Первое высшее техническое учебное заведение России
Санкт-Петербургский горный университет императрицы
Екатерины II
Лекция 1
Числовые ряды.
Гармоничеcкий ряд.
Ряд Дирихле
26.11.2025
г. СанктПетербург
2025
1/11

2.

Содержание лекции
•Основные понятия:
– числовой ряд,
– общий член ряда,
– частичная сумма и сумма числового ряда,
– сходимость ряда;
•Необходимый признак сходимости ряда
•Достаточные признаки сходимости рядов с
неотрицательными членами.
• Гармонический ряд
• Ряд Дирихле
2|11

3.

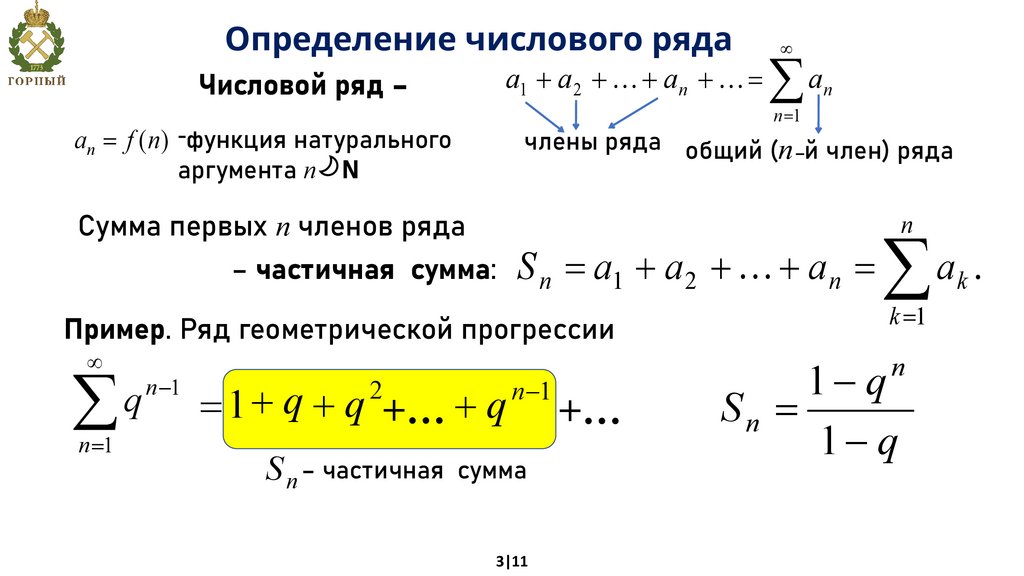
Определение числового ряда
Числовой ряд –
a1 a 2 a n
an f (n) -функция натурального
a
n
n 1
члены ряда общий (n –й член) ряда
аргумента n N
Сумма первых n членов ряда
– частичная сумма: S n a1 a 2 a n
Пример. Ряд геометрической прогрессии
n 1
q
n 1
1 q q +… q
2
n 1
S n – частичная сумма
3|11
n
a .
k
k 1
n
+…
1 q
Sn
1 q

4.

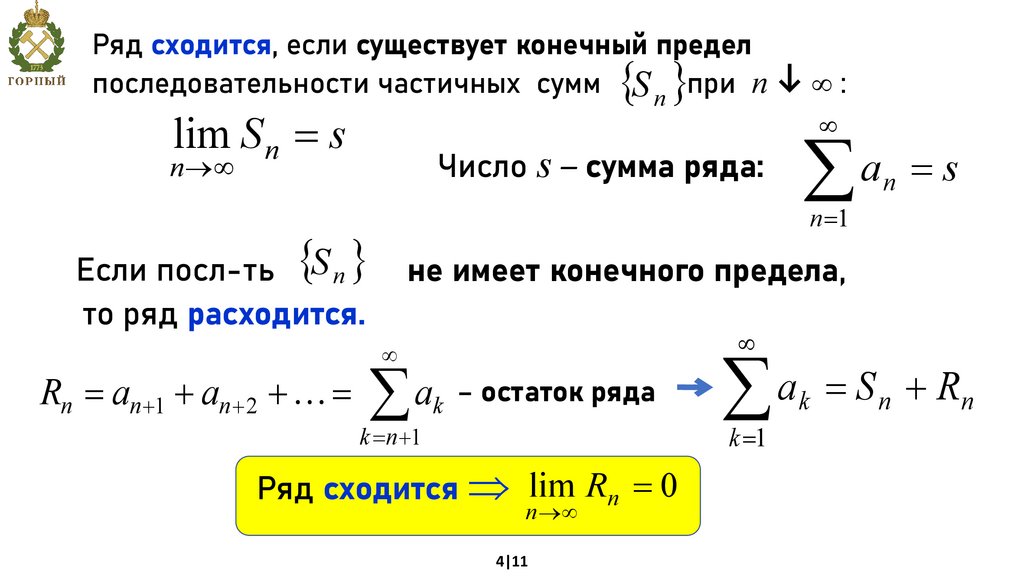
Ряд сходится, если существует конечный предел
последовательности частичных сумм S n при n :
lim S n s
Число s – сумма ряда:
n
an s
n 1
Если посл-ть S n
то ряд расходится.
Rn an 1 an 2
не имеет конечного предела,
ak – остаток ряда
k 1
k n 1
Ряд сходится lim Rn 0
n
4|11
a k S n Rn

5.

q
n 1
n 1
сходится при
q 1
расходится при
q 1
q 1 q q +… q
n 1
2
n 1
n
1 q
1
lim S n lim
n
n 1 q
1 q
n 1
1
+… 1 q
q 1
1
1
1
1
1
Пример . Найти сумму ряда1 2 2 3 3 4 n n 1 n n 1
n 1
1
1 1 1 1 1 1
1
1
1
Sn + + + … +
n n 1
n 1
1 2 2 3 3 4
0
1
(n 1) n 1
1
lim S n 1
n n 1
n n 1
n n 1
n
5|11

6.

Свойства сходящихся рядов
Теорема 1. Сходимость (расходимость) ряда не нарушится, если:
а) ряд умножить на число c 0;
б) к ряду прибавить (отбросить) конечное число слагаемых.
Теорема 2. Сходящиеся ряды можно почленно складывать и
вычитать, причем полученные ряды тоже сходятся.
Теорема 3 (необходимый признак сходимости)
an 0
a - сходится nlim
n 1
n
n-й член сходящегося ряда
стремится к 0 при n
an ¹ 0
Достаточный признак расходимости nlim
®¥
6|11
n 1
a n - расходится

7.

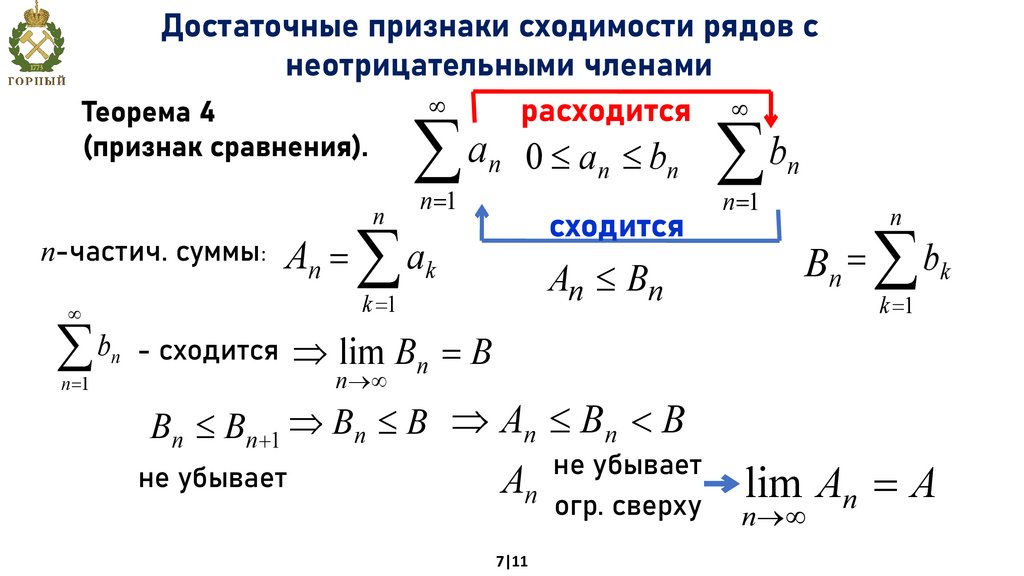
Достаточные признаки сходимости рядов с
неотрицательными членами
расходится
Теорема 4
(признак сравнения).
n
n
n-частич. суммы: A
n 1
a
a n 0 a n bn
сходится
An Bn
k
k 1
bn
n 1
n
Bn
Bn B
b - сходится nlim
bk
k 1
n
n 1
Bn Bn 1 Bn B An Bn B
не убывает
не убывает
An
огр. сверху
7|11
lim Аn А
n

8.

Теорема 5. признак сравнения в предельной форме
an
lim
k , k 0, a n
n b
n
n 1
1
Пример. sin n
2
n 1
оба
сходятся
(расходятся)
bn
одновременно
n 1
1
сходится
n
n 1 2
1
1
n
при n sin
n
2
2
l 1 – сходится
Теорема 6
an 1
– доп. исследование
lim
l
l
1
(признак Даламбера) n a
n
l 1 – расходится
Пример. Исследовать на сходимость ряды
3
n
5n
n 1
arctg n
2
n 1
9|11

9.

Теорема 7 (радикальный признак Коши).
l 1 – сходится
lim n a n l l 1 – доп. исследование
n
l 1 – расходится
Пример. Исследовать на сходимость ряд
n 1
Теорема 8 (интегральный признак Коши)
При х [1, )
f(x) 0,
непрерывна,
убывает
a n f ( n) 0
n 1
10|11
an
5n
1
1
n
n2
сходятся
расходятся
1
f ( x)dx

10.

у=f(x)
f(k+1)
f(k+1) f(x) f(k)
k 1
k
f ( x)dx f(k)
n
n 1
n
k 1
1
k 1
f(k+1) f ( x)dx f(k)
1 2
k k+1
n n+1
f(2)+ …+ f(n+1)
n 1
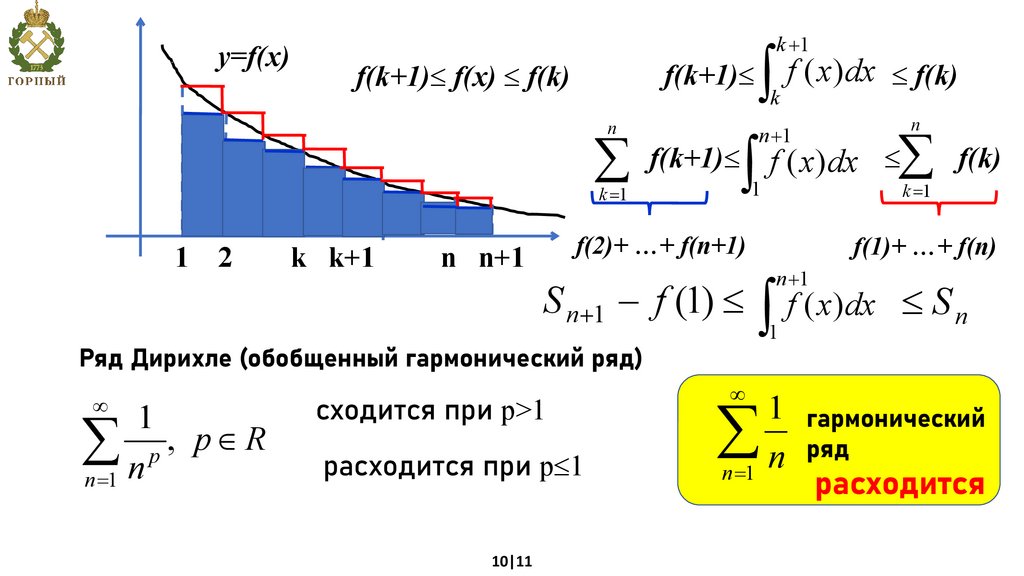
S n 1 f (1) f ( x)dx S n
1
Ряд Дирихле (обобщенный гармонический ряд)
1
,
p
R
p
n 1 n
сходится при p>1
расходится при p 1
10|11
f(1)+ …+ f(n)
1 гармонический
ряд
n
n 1
расходится

11.

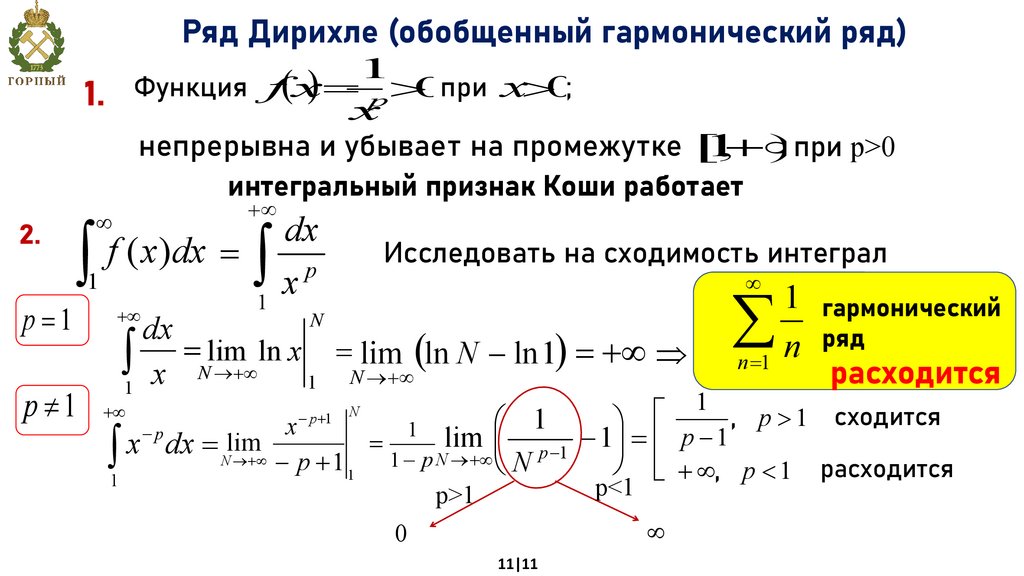
Ряд Дирихле (обобщенный гармонический ряд)
1.
1
Функция f x
p 0при x 0;
x
непрерывна и убывает на промежутке [1
,
) при p>0
интегральный признак Коши работает
2.
p 1
dx
f ( x)dx
p
1
x
1
Исследовать на сходимость интеграл
1 гармонический
ряд
n
n 1
N
dx
ln х lim ln N ln 1
1 x Nlim
расходится
N
1
1
N
p 1
p 1
, p 1 сходится
1
x
1
p
lim p 1 1 p 1
lim
x
dx
1
N p 1
1 p N N
, p 1 расходится
1
p<1
p>1
0
11|11