10

1. Аналитикалық геометрия және сызықтық алгебра

Қазақстан Республикасының Білім және ғылым министрлігі
Қарағанды Бөкетов университеті
Математика және ақпараттық технологиялар факультеті
Тақырыбы: Екінші ретті беттер және олардың канондық теңдеулері
«6В05304-Физика» білім беру бағдарламасы
Авторлар:
Медеубаев Н.Қ., проф. Т.Ғ.Мұстафин атындағы алгебра, мат. логика және геометрия кафедрасының
аға оқытушысы, РһD.
Оразбекова Р.Т., проф. Т.Ғ.Мұстафин атындағы алгебра, мат. логика және геометрия кафедрасының
аға оқытушысы, математика магистры.
Сабақ түрі: дәріс
Қарағанды 2022

2.

Екінші ретті беттер – координаталар жүйесінде екінші дәрежелі
теңдеумен кескінделетін беттер.
Екінші ретті беттің жалпы теңдеуі: F(x,y,z)=0.
Бұл x,y,z-ке тәуелді функция. Оның коэффициенттері нақты, бүтін
рационалды болады.

3.

1. Сфера.
Берілген нүктелерден әрқашанда бірдей қашықтықта тұратын кеңістіктегі нүктелердің
геометриялық орындарын сфералық немесе шар беті дейміз
Егер сфераның центрі C(a,b,c) нүктесі және оның бетіндегі кез келген M(x,y,z) нүктесі берілсе,
онда CM=R оның радиусы болады.
Кеңістіктегі екі нүктенің арасындағы қашықтықтың формуласы бойынша сфераның теңдеуін
табайық.
R CM ( x a) 2 ( y b) 2 ( z c) 2
( x a) 2 ( y b) 2 ( z c) 2 R 2
Бұл теңдеу сфераның нормальдық теңдеуі
Егер сфераның центрі координатаның бас нүктесінде болса,
онда a=b=c=0 болады да, (x a) 2 ( y b) 2 (z c) 2 R 2
теңдеуі мына түрге келеді:
x 2 y 2 z 2 R2
R
C

4.

Сфераның нормальдық теңдеуін түрлендірейік:
x 2 2ax a 2 y 2 2by b 2 z 2 2cz c 2 R 2 0
немесе
x 2 y 2 z 2 Ax By Cz D 0
Бұл теңдеу сфералық беттің жалпы теңдеуі деп аталады, мұндағы,
A 2a, B 2b, C 2C
D a2 b 2 c 2 R 2
Сфералық (x a) 2 ( y b) 2 (z c) 2 R 2 теңдеуі және оның бетінде жатқан бір M 1 ( x1 , y1 , z1 ) нүктесі
берілген. Сфераны осы берілген нүктеден жанап өтетін жазықтың теңдігін табайық. Ол мына түрде
жазылады.
( x1 a)(x a) ( y1 b)( y b) ( z1 c)(z c) R 2
Егер сфераның центрі координатасының бас нүктесінде, яғни a=b=c=0 болса, онда оған жүргізген
жанама жазықтық мынадай болады
xx1 yy1 zz1 R 2

5.

2. Цилиндр
Цилиндр кеңістіктегі геометриялық бейне.
Ол төрт түрге бөледі: дөңгелек цилиндр, эллипстік цилиндр, гиперболалық, параболалық
цилиндр.
Осыған сәйкес цилиндр тіқ бұрышты координаталар жүйесінде төрт түрлі теңдеумен анықталады.
x y R
2
2
2
x2 y2
2 1
2
a
b
x2 y2
2 1
2
a
b
y 2 2 px
Бұл төрт теңдеу жазықтықта шеңберді, эллипсті, гиперболаны, параболаны кескіндейді, ал
кеңістікте дөңгелек цилиндрді, эллипстік, гиперболалық және параболалық цилиндрлерді
кескіндейді.

6.

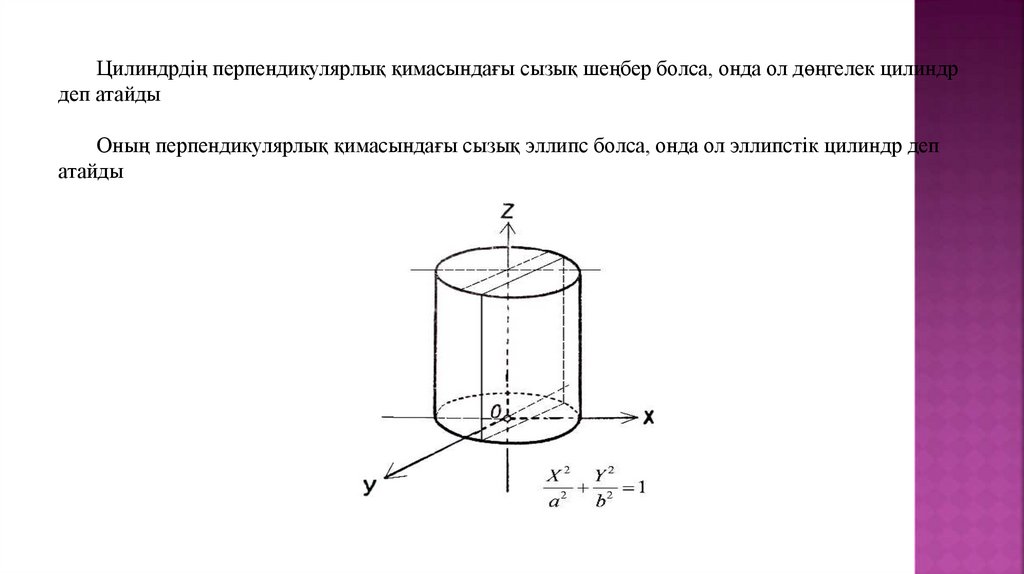
Цилиндрдің перпендикулярлық қимасындағы сызық шеңбер болса, онда ол дөңгелек цилиндр
деп атайды
Оның перпендикулярлық қимасындағы сызық эллипс болса, онда ол эллипстік цилиндр деп
атайды

7.

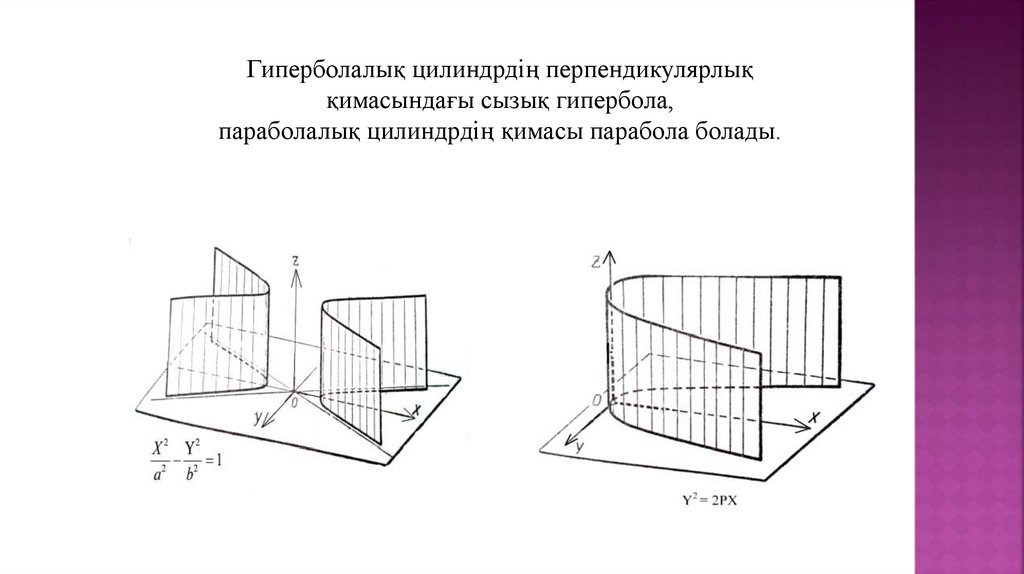
Гиперболалық цилиндрдің перпендикулярлық
қимасындағы сызық гипербола,
параболалық цилиндрдің қимасы парабола болады.

8.

3. Конус.
Екінші ретті конус деп, берілген нүктеден өтетін және бағыттаушы қисықтың бойымен
жылжитын жасаушы түзудің үздіксіз қозғалғанынан шыққан геометриялық бейнені айтамыз.
Конустың бағыттаушысы эллипс болсын. Конусты XOY жазықтығына параллель қиып өтетін
жазықтық z=c болсын. Конус жасаушы түзуі координаталардың бас нүктесінен өтсін, яғни конустың
төбесі координаталардың бас нүктесінде жатсын. Осы конустың теңдеуін іздейік.
Бұл теңдеу мына түрде жазылады:
x2 y2 z2
2 2 0
2
a
b
c
бұл z осінің жанымен қозғалатын айналмалы конус деп аталады.
Егер a b c болса, онда мынадай конус шығады:
x2 y2 z2 0

9.

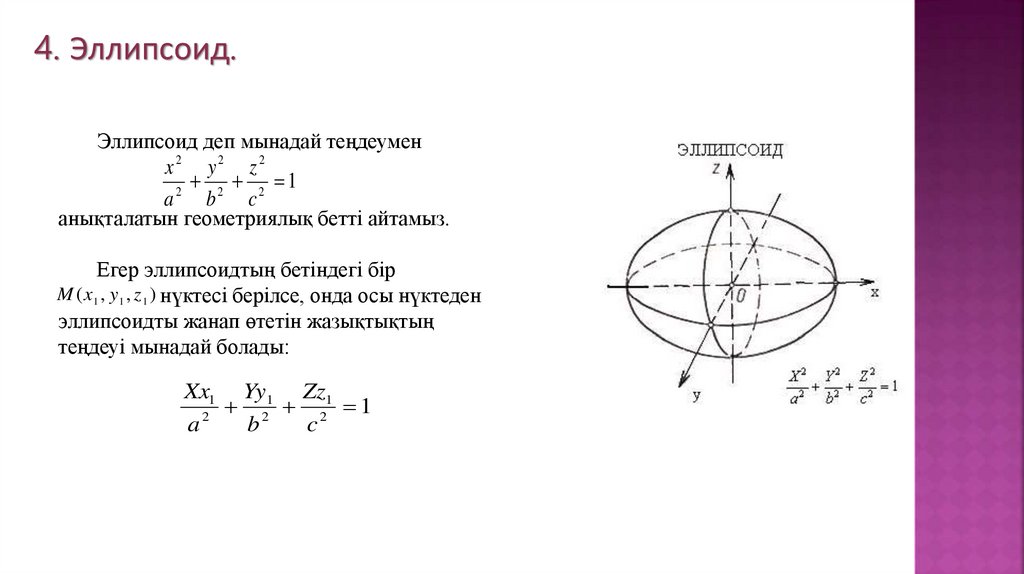
4. Эллипсоид.
Эллипсоид деп мынадай теңдеумен
x2 y2 z2
2 2 1
2
a b c
анықталатын геометриялық бетті айтамыз.
Егер эллипсоидтың бетіндегі бір
M ( x1 , y1 , z 1 ) нүктесі берілсе, онда осы нүктеден
эллипсоидты жанап өтетін жазықтықтың
теңдеуі мынадай болады:
Xx1 Yy1 Zz1
2 2 1
2
a
b
c

10.

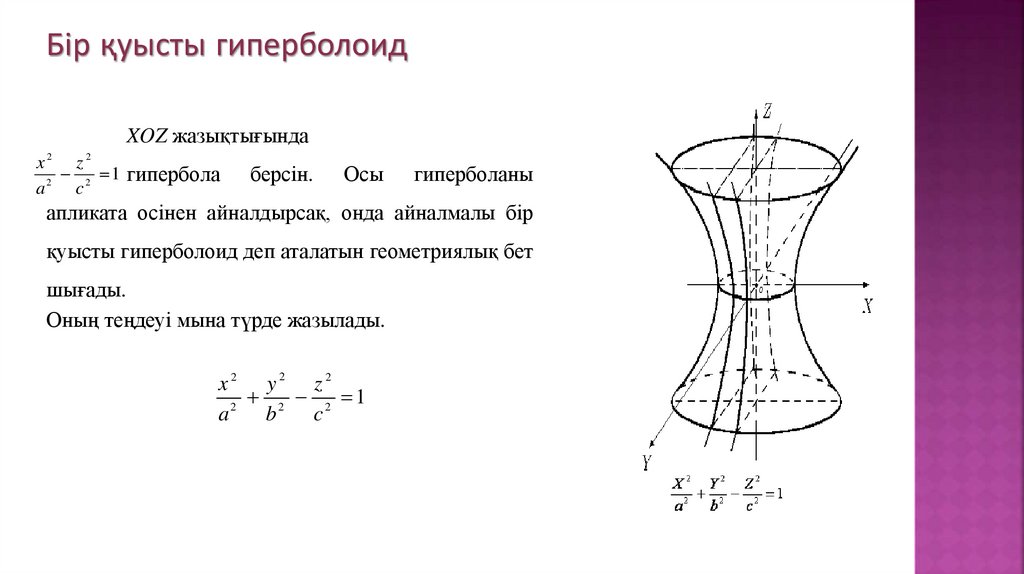
Бір қуысты гиперболоид
XOZ жазықтығында
x2 z2
1 гипербола
a2 c 2
берсін.
Осы
гиперболаны
апликата осінен айналдырсақ, онда айналмалы бір
қуысты гиперболоид деп аталатын геометриялық бет
шығады.
Оның теңдеуі мына түрде жазылады.
x2 y2 z2
2 2 1
2
a
b
c

11.

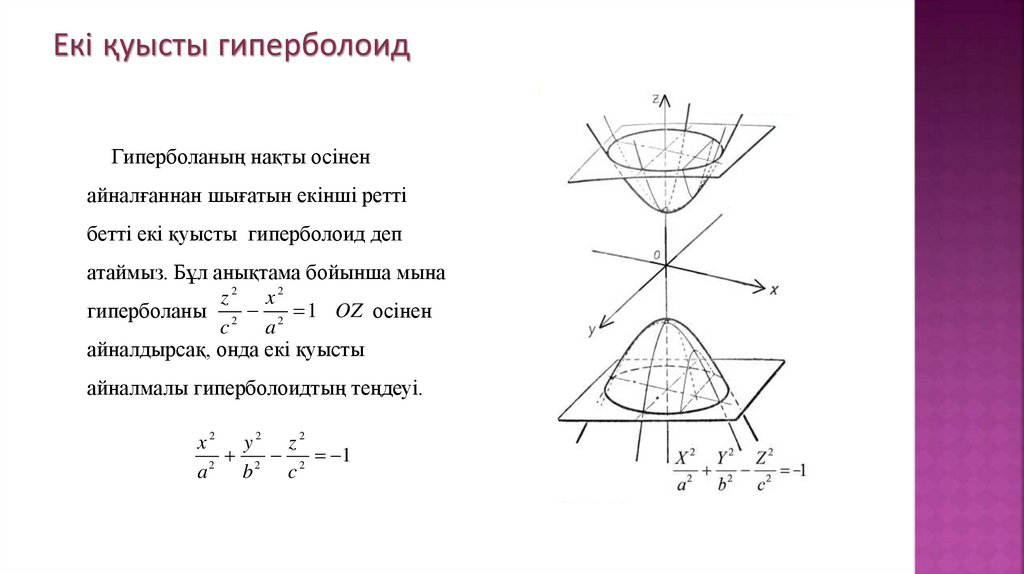
Екі қуысты гиперболоид
Гиперболаның нақты осінен
айналғаннан шығатын екінші ретті
бетті екі қуысты гиперболоид деп
атаймыз. Бұл анықтама бойынша мына
z2 x2
гиперболаны 2 2 1 OZ осінен
c
a
айналдырсақ, онда екі қуысты
айналмалы гиперболоидтың теңдеуі.
x2 y2 z2
2 2 1
2
a
b
c

12.

Эллипстік параболоид
Бізге x 2 2 pz параболасы берілген.
Осы параболаны Оz – осінен айналдырсақ, бізге белгілі формула бойынша мынадай жаңа теңдеумен
кескінделеді.
x2 y2
2z
p q
мұндағы p,q>0
Эллипстік параболоид деп,
x2 y2
2z
p q
теңдеуімен кескінделетін екінші ретті бетті айтамыз.
Эллипстік
параболоидты
қиып
өтетін
XOY
жазықтығына
параллель
z=h
жазықтығын
жүргізілген.

13.

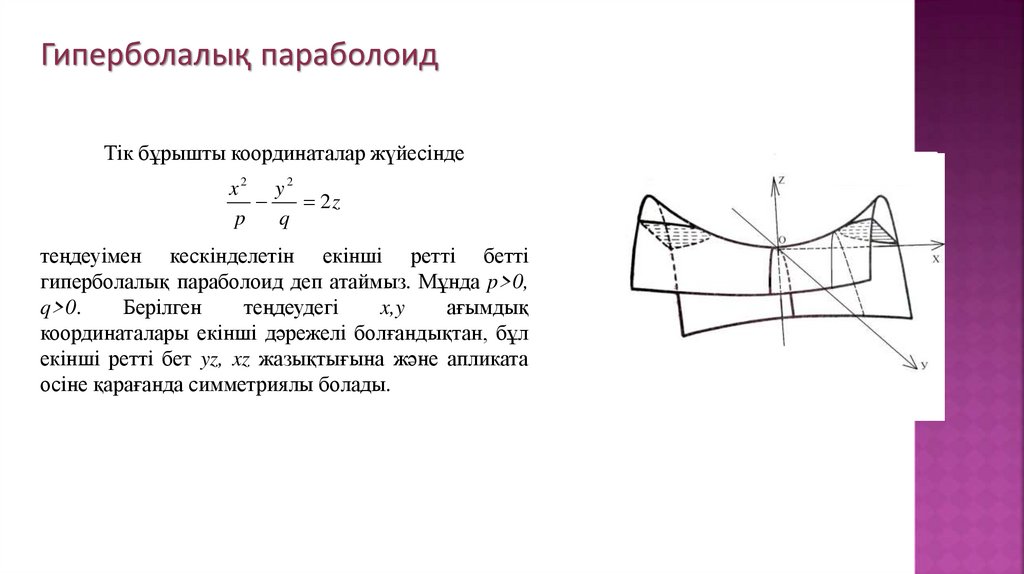
Гиперболалық параболоид
Тік бұрышты координаталар жүйесінде
x2 y2
2z
p
q
теңдеуімен кескінделетін екінші ретті бетті
гиперболалық параболоид деп атаймыз. Мұнда p>0,
q>0.
Берілген
теңдеудегі
x,y
ағымдық
координаталары екінші дәрежелі болғандықтан, бұл
екінші ретті бет yz, xz жазықтығына және апликата
осіне қарағанда симметриялы болады.

14.

1-мысал.
x2 y2 z 2
1 гиперболоид пен
2
4
2
y 2 жазықтығының қиылысуында жататын нүктені табу керек.
Шешуі.
Қиылысуында жататын нүктені табу үшін у-тің мәнін беттің теңдеуіне қоямыз.
Сонда шыққан теңдеуді қанағаттандыратын нүктелерді анықтаймыз.
x2 4
z2
1;
2
4
2
x2
z2
1
1;
2
2
x2 z2
0;
2
2
x2 z2
.
2
2
Жауабы:
Бұл есепте х пен z кез-келген модулі бойынша бірдей сандарды қанағаттандырады. Мысалы,
А(0;2;0) , В(-4;2;4) , С(5;2;-5)

15.

2-мысал.
x2 y2 z 2
1 эллипсоиды және
16 12 4
x 2 0 жазықтығының қиылысуынан шығатын қисықтың
жарты осьтері қандай болады?
Шешуі.
x=2 мәнін эллипсоидтың теңдеуіне қойып, шыққан эллипстің теңдеуін канондық түрге
келтіреміз.Одан эллипстің жарты осьтерін анықтаймыз.
1
y2 z2
1;
4 12 4
y2 z2 3
;
12 4 4
y2 z2
1.
9
3