Similar presentations:
Екі еселі f ( x, y )
1.
11.1–ҮТ1. Екі еселі f ( x, y )dxdy интегралды: 1) сыртқы интегD
ралы x бойынша интегралданатын; 2) сыртқы интегралы y
бойынша интегралданатын қайталама интеграл түрінде, екі
тәсілмен жазыңыз. Мұндағы D интегралдау аймағы көрсетілген
сызықтармен шенелген.
1.1. D :
y 4 x2 , y 3x , x 0.
1.2. D :
x 2 2 y , 5 x 2 y 6 0.
1.3. D :
x 8 y 2 , y 0,
y x.
1.4. D :
x 0,
y ln x.
1.5. D :
x 2 2 y , x y 0.
1.6. D :
y 2 x2 , y x2 .
1.7. D :
y x 2 2,
1.8. D :
x 0,
1.9. D :
y 2 2 x , x 2 2 y , x 1.
1.10. D :
x 0, y x , y 9 x2 .
1.11. D :
y2 2 x ,
1.12. D :
x 2 y2 , x y2 ,
y 0.
1.13. D :
y 0, x 2 y 12 0,
y lg x .
1.14. D :
x 0,
y x.
1.15. D :
y 0, y x , y 2 x2 .
1.16. D :
y 0, x y , y 8 x2 .
y 0,
y 1,
y x.
y 1,
y 3,
y x.
y x.
y 1,
y 3,
287
2.
1.17. D :y x ,
y 2 x 3.
1.18. D :
y 4 x2 , x 0, x 1, y 0.
1.19. D :
x 1, x 2,
1.20. D :
y 0, x2 y , x 1 y 2 .
1.21. D :
y 0, y 1, y x , x 4 y 2 .
1.22. D :
x 0,
1.23. D :
y 3 x2 ,
1.24. D :
x 0, x 2,
1.25. D :
x 0, y 0, y 1,
x 3 2 y2 1.
1.26. D :
x 9 y2 ,
y x,
y 0.
1.27. D :
x 2 y 6 0,
y x,
y 0.
1.28. D :
y x , 3x y 3,
y 3.
1.29. D :
x 0,
1.30. D :
x 0, y 0,
y 1,
y 0,
y 4,
y x2 .
y x.
y x.
y 1,
y 0,
y 1,
y x 2 4.
y log1/ 2 x .
y 1, x 4 y 2 .
2. Екі еселі интегралды көрсетілген сызықтармен шенелген D аймағы бойынша есептеңіз.
2.1. x2 y dxdy , D: y x 2 ,
x y2.
D
2.2. xy 2 dxdy , D : y x 2 ,
y 2 x.
D
2.3. x y dxdy , D : y 2 x ,
y x.
D
2.4. x 2 ydxdy , D : y 2 x ,
y x , x 0.
D
288
3.
2.5. x3 2 y dxdy , D: y x2 1, x 0, y 0.D
2.6. y x dxdy , D : y x ,
y x2.
D
2.7. 1 y dxdy , D : y 2 x , 5 y x.
D
2.8. x y dxdy , D : y x 2 1,
y x 2 1.
D
2.9. x y 1 dxdy , D : y 5 x ,
y x , x 3.
D
2.10. x 2 ydxdy , D : y x ,
y
D
1
x , x 2.
2
2.11. x y 2 dxdy , D: y x2 , y 1.
D
2.12. x 2 ydxdy , D : y 2 x 3 ,
y 0, x 1.
D
2.13. x2 y 2 dxdy , D: x y 2 , x 1.
D
2.14. xydxdy , D : y x 3 ,
y 0, x 2.
D
2.15. x y dxdy , D : y x 3 ,
y 8,
y 0, x 3.
D
2.16. x 2 x y dxdy , D : y 1 x 2 ,
y 0.
D
2.17. y 1 x dxdy , D : y 3 x ,
y x, x 0.
D
2.18. xy 3 dxdy , D : y 2 1 x , x 0.
D
2.19. x y 5 dxdy , D : y x 5, x y 5 0, x 0.
D
2.20. x y dxdy , D : y x 2 1, y 3.
D
289
4.
2.21. x 1 y 2 dxdy , D : y 3 x 2 ,y 3.
D
2.22. xy 2 dxdy , D : y x ,
y 0, x 1.
D
2.23. x3 y dxdy , D: x y 1, x y 2, x 1, x 0.
D
2.24. xy 3 dxdy , D : y x3 ,
y 0,
y 4 x.
D
2.25. x3 3 y dxdy , D: x y 1,
y x 2 1, x 0.
D
2.26. xydxdy , D : y x ,
y 0, x y 2.
D
y2
dxdy , D : y x , xy 1,
2
D x
2.27.
2.28. y 1 x2 dxdy , D: y x3 ,
y 2.
y 3x.
D
2.29. y 2 1 2 x dxdy , D : x 2 y 2 , x 0.
D
2.30. e y dxdy , D : y ln x ,
y 0, x 2.
D
3. Полярлық координаттарды пайдаланып қайталама
интегралды есептеңіз
1
1 x 2
0
0
3.1. dx
1 x2 y 2
dy.
1 x2 y 2
3.2.
R
R x2
0
R x2
3.3. dx
tg x 2 y 2
x2 y 2
1
3 x 2
3
0
dx
dy
1 x2 y 2
.
dy.
290
5.
13.4. dx
1 x2
ln(1 x y )dy.
0
2
4 y 2
2
4 y 2
3.5. dy
2
0
1 x 2 y 2 dx.
2
0
R2 x2
R
0
0
dx
3.6.
3.7. dx
R
R2 x2
0
R2 x2
2 x
R
R2 x2
R
0
cos x 2 y 2 dy.
3
3 x 2
3
0
dx
R
R2 x2
R
R2 x2
2 x2
dx
2
2
4 x2
0
4 x
sin x 2 y 2 dy.
1 x 2 y 2 dy.
3.12.
2
3.13. dx
tg x 2 y 2 dy.
cos x 2 y 2 dy.
3.10. dx
3.11.
xy
dy.
2
2 x y
2
2
3.8. dx
3.9. dx
2
1 x y dy.
2
2
2 x2
dy
.
2
2
2 1 x y
1
1 x 2
0
0
3.14. dx
dy
1 x2 y 2
.
291
6.
R0
3.15. dx
R
sin x 2 y 2
x2 y 2
R x2
dy.
R2 x2
R
3.16. dx
0
R
0
3.17. dx
R
R2 x2
x 2 y 2 sin 2 x 2 y 2
0
dy
R
x y ctg x 2 y 2
2
0
2
.
3
3
3.21. dx
R
0
0
cos x 2 y 2 dy.
R2 x2
1
1 x2
1
0
dx
0
R2 x2
R
0
3
0
sin x 2 y 2 dy.
1 x 2 y 2 dy.
2
4 x2
2
0
3.24. dx
3.25. dx
xy
dy.
2
2 x y
2
9 x
3.22. dx
3.23.
2
0
3.20. dx
0
.
xy
dy.
x y2
0
3.19. dx
2
.
4 x2
2
3.18. dx
R2 x2
x y cos 2 x 2 y 2
2
R2 x2
dy
dy
2
2
x 2 y 2 e x y dy.
9 x2
ln 1 x y dy.
2
2
0
2
2 x2
2
2 x2
3.26. dx
2
2
e ( x y ) dy.
292
7.
11 x 2
0
1 x 2
3.27. dx
ln(1 x 2 y 2 )
x2 y 2
dy .
2
3.28. dx
R
R2 x2
0
R2 x2
3.29. dx
4 x2
cos x y dy .
2
0
0
R
R2 x2
0
R2 x2
2
sin x 2 y 2 dy.
3.30. dx
tg x 2 y 2
x2 y 2
dy.
4. Берілген сызықтармен шенелген жазық D аймағының
ауданын есептеңіз
4.1. D : y 2 4 x , x y 3,
10
y 0. Жауабы :
3
5
4.2. D : y 6 x 2 , x y 2, x 0. Жауабы :
8
32
4.3. D : y 2 x 2, x 2. Жауабы :
3
16
4.4. D : x 2 y 2 , x 1 3 y 2 , x 0, y 0. Жауабы :
4.5. D : y
3
8
4
, x 2 4 y . Æàóàáû : 2
3
x 4
2
9
4.6. D : y x 2 1, x y 3. Жауабы :
2
16
4.7. D : y 2 4 x , x 2 4 y . Жауабы :
3
293
8.
5.9. x 2 y 2a 2x 3 y .
2
2
2
5.10. x 2 y 2
2
a 5x 3 y .
2
2
2
2
a 7x 5 y . 5.12. x y 2a xy.
5.13. x y 4 x y .
5.14. x y a y .
2
2
2 3
2
5.11. x 2 y 2
2
5.15. x 2 y 2
2
2
2
a x .
3
2
2 2
2
2 3
2
4
2
5.16. a cos 2
4 2
5.17. 2 a 2 (1 sin 2 )
5.18. x 2 y 2
a x .
3
2 4
5.19. x 2 y 2
4 3x 4 y .
2
5.20. x 2 y 2
a x y .
5.21. x 2 y 2
a ( x y ).
5.22. x 2 y 2
2ay .
4a xy( x y ).
5.23. x 2 y 2
2
3
2
2
3
4
2
4
2
2
3
2 2
3
2
3
5.24. a sin 2
5.25. a cos5
5.26. 4(1 cos )
5.27. 2a(2 cos )
5.28. 2 a 2 cos3
5.29. 2 a 2 cos 2
5.30. a sin3
6. Берілген беттермен шенелген дененің көлемін есептеңіз
1
6.1. z x2 y 2 , x y 1, x 0, y 0, z 0. (Жауабы : )
6
53
6.2. z 2 ( x2 y 2 ), x 2 y 1, x 0, y 0, z 0. (Жауабы : )
96
6.3. z x 2 , x 2 y 2 0, x y 7 0, z 0.
6.4. z 2 x2 3 y 2 ,
y x2 ,
( Жауабы : 32)
y x , z 0. (Жауабы :
29
)
140
6.5. z 2 x2 y 2 , y x , y 3x , x 2, z 0. (Жауабы :
152
)
3
296
9.
6.6. z x, y 4, x 25 y 26.7. y x ,
x 0 y 0 z 0. (Жауабы :
y x , x y z 2, z 0. (Жауабы :
6.8. y 1 x 2 , x y z 3,
y 0,
6.9. z 2 x 2 y 2 , x y 4, x 0,
118
)
3
11
)
60
z 0. (Жауабы :
104
)
30
y 0, z 0. ( Жауабы : 64)
6.10. z 4 x 2 , x 2 y 2 4, x 0, y 0, z 0. ( Жауабы : 3 )
6.11. 2 x 3 y 12 0, 2 z y 2 , x 0, y 0, z 0. ( Жауабы :16)
65
)
12
6.13. z x 2 , x y 6, y 2 x, x 0, y 0, z 0. ( Жауабы : 4)
6.12. z 10 x2 2 y 2 , y x , x 1, y 0, z 0. (Жауабы :
264 2
)
35
303
6.15. 3 y x , y x, x y z 10, y 1, z 0. (Жауабы :
)
20
49
6.16. y 2 1 x , x y z 1, x 0, z 0.
(Жауабы : )
60
11
6.17. y x2 , x y 2 , z 3x 2 y 6,
z 0. (Жауабы : )
4
52
6.18. x2 1 y , x y z 3, y 0, z 0. (Жауабы : )
15
68
6.19. x y 2 , x 1, x y z 4,
z 0. (Жауабы : )
15
1
6.20. z 2 x 2 y 2 , x y 1, x 0, y 0, z 0. (Жауабы : )
4
704
6.21. y x2 , y 4, z 2 x 5 y 10, z 0. (Жауабы :
)
3
6.14. z 3x 2 2 y 2 1,
y x 2 1,
y 1 z 0 (Жауабы :
297
10.
11.2–ҮТ1. V аймағы көрсетілген беттермен шенелген. Интегралдау
аймағын сызыңыз. Үш еселі f x, y , z dxdydz интегралының
V
интегралдау шектерін қойыңыз.
1.1. V : x 2, y 4 x, y 3 x ; z 0, z 4 .
1.2. V : x 1, y 3x, y 0; z 0, z 2 x 2 y 2 .
1.3. V : x 1, y 4 x, z 0, z 3 y .
1.4. V : x 3, y x, y 0; z 0, z 3x 2 y 2 .
1.5. V : y 2 x, y 2; z 0, z 2 x .
1.6. V : x 0, y x, y 5; z 0, z 2 x 2 y 2 .
1.7. V : x 0, y 2 x, y 1; z 0, x y z 3 .
1.8. V : x 0, y 3x, y 3; z 0, x 3 z .
x
1.9. V : x 5, y , y 0; z 0, z x 2 5 y 2 .
5
1.10. V : x 2, y 4 x, z 0, y 2 z .
x
1
1.11. V : x 3, y , y 0; z 0, z x 2 y 2 .
3
2
x
1.12. V : x 4, y , z 0, z 4 y 2 .
4
1.13. V : x 0, y 3x, y 3; z 0, z 2 x 2 y 2 .
1.14. V : x 0, y 4 x, y 8; z 0, z 3x 2 y 2 .
1.15. V : x 0, y 5 x, y 10; z 0, z x 2 y 2 .
1.16. V : y x, y x, y 2; z 0, z 3 x 2 y 2 .
303
11.
1.17. V : x 1, y 2 x, y 3x; z 0, z 2 x 2 y 2 .1.18. V : y x, y 2 x, y 1; z 0, z x 2 4 y 2 .
1.19. V : x 0, y 0, z 0, x y 1, z 3x 2 2 y 2 .
1.20. V : x 0, y 0, z 0, 3x 2 y 6, z x 2 y 2 .
1.21. V : x 0, y 0, z 0, x y 3, z 9 x 2 y 2 .
1.22. V : x 0, y 0, z 0, x y 3, z 9 x 2 y 2 .
1.23. V : x 0, y 0, z 0, 3x 4 y 12, z 6 x 2 y 2 .
1.24. V : x 0, z 0, y x, y 3, z 18 x 2 y 2 .
1.25. V : x 2, y 0, z 0, y 3x, z 4 x 2 y 2 .
1.26. V : x 0, y 2 x, y 4, z 0, z 10 x 2 y 2 .
1.27. V : x 3, y 0, z 0, y 2 x, z 4 y .
1.28. V : x 0, y 0, z 0, 2 x 3 y 6,
z 3 x2 y 2 .
1.29. V : x 0, y 0, z 0, x y 4, z 16 x 2 y 2 .
1.30. V : x 0, y 0, z 0, 5 x y 5, z x 2 y 2 .
2. Берілген үш еселі интегралдарды есептеңіз.
2.1. 2 x2 3 y z dxdydz, V : 2 x 3, -1 y 2, 0 z 4.
V
2.2. x 2 yzdxdydz , V : 1 x 2, 0 y 3, 2 z 3.
V
2.3. x y 4 z 2 dxdydz, V : 1 x 1, 0 y 2, 1 z 1.
V
2.4. x2 y 2 z 2 dxdydz, V : 0 x 3, 1 y 2, 0 z 2.
V
2.5. x 2 y 2 zdxdydz , V : 1 x 3, 0 y 2, 2 z 5.
V
304
12.
2.6. x y z dxdydz , V : 0 x 1, 1 y 0, 1 z 2.V
2.7. 2 x y 2 z dxdydz, V :1 x 5, 0 y 2, 1 z 0.
V
2.8. 2 xy 2 zdxdydz , V : 0 x 3, 2 y 0, 1 z 2.
V
2.9. 5 xyz 2 dxdydz , V : 1 x 0, 2 y 3, 1 z 2.
V
2.10. x2 2 y 2 z dxdydz, V : 0 x 1, 0 y 3, 1 z 2.
V
2.11. x 2 yz dxdydz, V : 2 x 0, 0 y 1, 0 z 2.
V
2.12. x yz 2 dxdydz, V : 0 x 1, 0 y 2, 1 z 3.
V
2.13. xy 3z dxdydz, V : 1 x 1, 0 y 1, 1 z 2.
V
2.14. xy z 2 dxdydz, V : 0 x 2, 0 y 1, -1 z 3.
V
2.15. x3 yz dxdydz, V : 1 x 2, 0 y 1, 0 z 1.
V
2.16. x3 y 2 z dxdydz, V : 0 x 2, 1 y 0, 0 z 1.
V
2.17. 2 x2 y z 3 dxdydz, V : 0 x 1, 2 y 1, 0 z 1.
V
2.18. x 2 yz 2 dxdydz , V : 0 x 2, 1 y 2, 1 z 0.
V
2.19. x y z dxdydz, V : 0 x 4, 1 y 3, 1 z 5.
V
2.20. x 2 y 3z 2 dxdydz, V : 1 x 2, 0 y 1, 1 z 2.
V
305
13.
2.22. xy z dxdydz, V : 0 x 1, 1 y 2, 0 z 3.2.21. 3x2 2 y z dxdydz, V : 0 x 1, 0 y 1, 1 z 3.
V
3
V
2.23. x3 yzdxdydz , V : 1 x 2, 1 y 3, 0 z 1.
V
2.24. xy 2 zdxdydz , V : 2 x 1, 0 y 2, 0 z 3.
V
2.25. xyz 2 dxdydz , V : 0 x 2, 1 y 0, 0 z 4.
V
2.26. x yz dxdydz , V : 0 x 1, 1 y 4, 0 z 2.
V
2.28. x y z dxdydz, V : 1 x 0, 0 y 1, 2 z 3.
2.29. x y 2 z dxdydz, V :1 x 2, 2 y 3, 0 z 1.
2.27. x y 2 z 2 dxdydz, V : 2 x 0, 1 y 2, 0 z 5.
V
2
V
2
V
2.30. x y z dxdydz, V : 0 x 3, 0 y 1, 2 z 1.
V
3. Үш еселі интегралды цилиндрлік немесе сфералық
координаттар көмегімен есептеңіз
3.1. x2 y 2 z 2 dxdydz, V : x2 y 2 z 2 4, x 0, y 0, z 0.
V
(Жауабы:
16
.)
5
3.2. y x2 y 2 dxdydz, V : z 0, z 2 y x, z 2 4 x 2 y 2 .
V
(Жауабы:
2
.)
10
3.3. z 2 dxdydz , V :1 x 2 y 2 36, x 0, y x, z 0.
V
306
14.
1555.)
12
(Жауабы:
3.4. ydxdydz , V : x 2 y 2 z 2 32, y 2 x 2 z 2 , y 0.
V
(Жауабы: 128 .)
3.5. xdxdydz , V : x y z 8, x y z , x 0.
2
2
2
2
2
2
V
(Жауабы: 8 .)
3.6. ydxdydz , V : 4 x y z 16, y 3 x , y 0, z 0.
2
2
2
V
(Жауабы:
15
.)
2
3.7. ydxdydz, V : z 8 x2 y 2 , z x 2 y 2 , y 0.
V
(Жауабы: 8 1 .)
2
3.8.
V
y 2 dxdydz
x y z
2
2
2
, V : x 0, y 3x , z 0, 4 x 2 y 2 z 2 36.
3.9.
V
y 2 zdxdydz
x y
2 3
2
52
2 3 3 .)
27
(Жауабы:
, V : y 0, y 3x , z 3 x 2 y 2 , z 3.
3 4 3 3
(Жауабы:
3.10.
V
2
x dxdydz
x y z
2
2
2 3
20
.)
, V : x 2 y 2 z 2 16, z 0.
(Жауабы:
16
.)
3
307
15.
22
5 2
0
1
I y 2 d d dy d 3d dy
V
2
2
0
0
0
5 2
d y 1
2
2
0
0
3 d d 3 (5 2 1)d
2
26 2
32
4
d
(2
) d .
0
6 0
3
6
( 4 )
6
0
2
▲
11.4–ҮТ
Берілген қисық сызықты интегралдарды есептеңіз.
1
x 2 xy dx y 2 xy dy ,
2
1.1.
2
LAB
параболасының A 1,1 нүктесінен
доғасы.
(Жауабы: – 6.)
1.2.
LAB
x 2 dy y 2 dx
3
x y
5
3
5
мұнда
B 1,1
LAB :
y x2
нүктесіне дейінгі
, мұнда LAB : x 2cos3 t , y 2sin 3 t астро-
идасының A 2,0 нүктесінен B 0, 2 нүктесіне дейінгі доғасы.
3 3 2
.)
8
кубтық пара-
(Жауабы:
1.3.
x y dx 2 xydy, мұнда LOA : y x
2
2
3
LOA
боласының O 0, 0 нүктесінен A 1,1 нүктесіне дейінгі доғасы.
4
.)
3
1.4. x 2 y dx x y dy , мұнда L : айналу бағыты оң
(Жауабы:
L
x 2cos t , y 2sin t шеңбері.
(Жауабы: 4 . )
327
16.
1.5. x2 y x dx y 2 x 2 y dy, мұнда L : айналу бағыты оңL
(Жауабы: 7,5 .)
x 3cos t , y 2sin t эллипсінің доғасы .
xy 1 dx x ydy ,
2
1.6.
мұнда
L AB :
x cos t , y 2sin t
LAB
эллипсінің A 1, 0 нүктесінен B 0, 2 нүктесіне дейінгі доғасы.
(Жауабы:
2 xydx x dy ,
2
1.7.
4
.)
3
мұнда LOBA : OBA сынық сызығы,
LOBA
O 0, 0 ; B 2, 0 ; A 2,1 .
(Жауабы: –4.)
x y dx xydy , мұнда LAB : AB – түзуінің кесіндісі,
2
1.8.
2
LAB
5
(Жауабы: 11 .)
6
1.9. cos ydx sin xdy, мұнда LAB : AB түзуінің кесіндісі,
A 1,1 ; B 3, 4 .
LAB
A 2 , 2 ; B 2 , 2 .
1.10.
ydx xdy
,
x2 y 2
L AB
мұнда LAB : AB түзуінің кесіндісі;
4
ln 3 .)
5
xydx y x dy , мұнда LAB : y x3 кубтық парабо-
A 1, 2 ; B 0, 2 .
1.11.
(Жауабы: 0.)
(Жауабы:
LAB
ласының A 0, 0 нүктесінен B 1,1 нүктесіне дейінгі доғасы.
1
.)
4
x 2 y 2 dx x y 2 dy , мұнда LABC : ABC сынық
(Жауабы:
1.12.
LABC
328
17.
сызығы; A 1, 2 ; B 3, 2 ; C 3, 5 . (Жауабы: 641.13.
xy dx yz dy x zdz,
2
2
мұнда
2
2
.)
3
LOB : OB түзуінің
LOB
кесіндісі; O 0, 0, 0 ; B 2, 4, 5 .
1.14.
ydx xdy,
мұнда
(Жауабы: 91.)
LOA :
x R cos t,
y R sin t
LOA
шеңберінің доғасы, O R,0 ; A 0, R .
1.15.
(Жауабы: 0.)
xydx y x dy, мұнда LOA : y x параболасының
2
LOA
O 0, 0 нүктесінен A 1,1 нүктесіне дейінгі доғасы.
(Жауабы:
1.16.
xdx ydy x y 1 dz, мұнда LAB : AB
17
.)
30
түзуінің
LAB
кесіндісі, A 1,1,1 , B 2,3, 4 .
1.17.
(Жауабы: 7.)
xy 1 dx x ydy, мұнда LAB :
y2 4 4x
2
пара-
LAB
боласының A 1, 0 нүктесінен B 0, 2 нүктесіне дейінгі доғасы.
17
.)
15
параболасының
(Жауабы:
1.18.
xydx y x dy, мұнда LOB: y x
2
LOB
O 0, 0 нүктесінен B 1,1 нүктесіне дейінгі доғасы.
1
.)
12
параболасы-
(Жауабы:
1.19.
xy y dx xdy, мұнда LOB:
2
y x2
LOB
ның O 0, 0 нүктесінен B 1,1 нүктесіне дейінгі доғасы.
329
18.
43.)
60
xdy ydx , мұнда LAB : x 2cos3 t , y 2sin 3 t астро-
(Жауабы:
1.20.
LAB
идасының A(2,0) нүктесінен B(0,2) нүктесіне дейінгі доғасы.
(Жауабы:
1.21.
1
xy y dx 2 x dy, мұнда LAB : y 4 x
2
2
3
.)
4
парабола-
LAB
сының A 0, 0 нүктесінен B 1, 2 нүктесіне дейінгі доғасы.
(Жауабы: 0,5.)
2
1.22. xy 1 dx x ydy, мұнда LAB : AB түзуінің кесінLAB
дісі, A 1, 0 ; B 0, 2 .
(Жауабы: 1.)
2 xydx y dy z dz, мұнда LAB : x cos t,
2
1.23.
2
y sin t ,
LAB
z 2t винттік сызығының бір орамы, A 1, 0, 0 ; B 1, 0, 4 .
(Жауабы: 64 3 / 3 .)
1.24.
y
dx xdy , мұнда LAB : y ln x сызығының A 1, 0
LAB x
нүктесінен B e,1 нүктесіне дейінгі доғасы.
(Жауабы: e 1/ 2 .)
1.25. ydx xdy , мұнда L : x 3cos t , y 2sin t эллипсінің
L
(Жауабы: 12 .)
оң бағытпен алынған доғасы,
1.26.
2 xydx x dy, мұнда LOA : y x / 4 параболасының
2
2
LOA
O 0, 0 нүктесінен A 2, 1 нүктесіне дейінгі доғасы.
(Жауабы: 0.)
330
19.
x y dx x y dy , мұнда LAB : y x2
1.27.
2
2
сызы-
2
LAB
ғының A 1,1 нүктесінен B 2, 2 нүктесіне дейінгі бөлігі.
(Жауабы: 6.)
2 xydx x dy zdz, мұнда LOA : түзудің O 0, 0, 0
2
1.28.
LOA
мен A 2, 1, 1 нүктелерін қосатын кесіндісі.
xdy ydx,
1.29.
мұнда L : төбелері
(Жауабы: 11/ 6 .)
A 1, 0 ,
B 1, 0 ,
L
C 0, 1 болатын үшбұрыштың оң бағытпен алынған контуры.
(Жауабы: 2.)
x y dx x y dy , мұнда LACB : ACB сынық
2
1.30.
2
LACB
сызық, A 2, 0 ; C 5, 0 ; B 5, 3 .
(Жауабы: 63.)
2
2.1. 2 z 2 2 z x 2 y 2 dl , мұнда L: x t cos t , y t sin t ,
L
z t , 0 t 2 қисығының доғасы. (Жауабы: 4 2 1 2 .)
2.2. x2 y 2 dl , мұнда L : x 2 y 2 4 шеңбері.
L
(Жауабы: 16 .)
2.3.
LOB
dl
8 x2 y 2
,
мұнда LOB : түзудің O 0, 0 және
B 2, 2 нүктелерін қосатын кесіндісі.
(Жауабы: / 2. )
331
20.
4 x 3 y dl ,3
2.4.
мұнда LAB : AB түзуінің кесіндісі;
LAB
A 1, 0 ; B 0, 1 .
2.5.
L AB
(Жауабы: 5 2 .)
dl
, мұнда LAB : түзудің A 0, 4 және B 4, 0
5 x y
нүктелерін қосатын кесіндісі.
(Жауабы: 0.)
y
dl , мұнда L : 2 1 cos , 0 / 2
2.6.
L
x2 y 2
кардиоидасының доғасы.
ydl ,
2.7.
16
.)
3
x cos3 t ,
(Жауабы:
мұнда LAB :
y sin 3 t
кардиои-
LAB
дасының A(1,0) мен B(0,1) нүктелерінің арасындағы доғасы.
(Жауабы: 0,6 .)
2
2.8. ydl , мұнда LOB : y 2 x параболасының O 0, 0
3
LOB
35 35
26
және B
нүктелерінің арасындағы доғасы. (Ж: 7
.)
6 , 3
27
2.9. x2 y 2 z 2 dl , мұнда L : x cos t, y sin t , z 3t ,
L
0 t 2 қисығының доғасы.
(Жауабы: 4 1 4 2 .)
y
2.10. arc tg dl , мұнда L : 1 cos , 0 кардиоx
2
L
идасының доғасы.
2.11.
(Жауабы: 2 2 8 .)
2 ydl , мұнда L :
x 2 t sin t ,
y 2 1 cos t
L
циклоидасының бірінші аркасы.
(Жауабы: 8 2 .)
332
21.
dl2.12.
x2 y 2 4
LOA
,
мұнда LOA : түзудің O 0, 0 мен
A 1, 2 нүктелерін қосатын кесіндісі.
(Жауабы: ln
5 3 / 2 .)
y x dl , мұнда L : 9sin 2 , 0
2.13.
4
x y
L
2
2
2
2 2
9
(Жауабы: .)
8
xydl , мұнда LOABC : төбелері O 0, 0 , A 4,0 ,
қисығының доғасы.
2.14.
LOABC
B 4, 2 , C 0, 2 болатын үшбұрыш контуры.
x y dl ,
2.15.
(Жауабы: 24 .)
мұнда LABO : төбелері A 1, 0 , B 0, 1 ,
LABO
O 0, 0 болатын үшбұрыш контуры.
(Жауабы: 2 .)
z 2 dl
x 2 y 2 , мұнда L : x 2cos t ,
L
2.16.
16
2 3 .)
3
x y dl , мұнда LOAB : төбелері O 0; 0 , A 1, 0 ,
винттік сызығының бірінші орамы.
2.17.
y 2sin t , z 2t
(Жауабы:
LOAB
B 0,1 болатын үшбұрыш контуры.
(Жауабы: 0 .)
2.18. x y dl , мұнда L : 2 cos 2 ,
Бернулли
4
4
L
лемнискатасының доғасы.
(Жауабы:
2 .)
2.19. x2 y 2 dl , мұнда L : x 2 y 2 2 y шеңбері.
L
(Жауабы: 8 .)
333
22.
xydl , мұнда LOABC : төбелері O 0, 0 , A 5, 0 ,2.20.
LOABC
B 5, 3 , C 0, 3 болатын үшбұрыш контуры.
(Жауабы: 15 .)
2.21. x y dl , мұнда L : x y 4 x шеңбері.
2
2
2
2
L
(Жауабы: 32 .)
2.22. 4 x 3 3 y dl ,
3
мұнда LAB :
x cos3 t ,
y sin 3 t
LAB
астроидасының A 1, 0 мен B 0, 1 нүктелерінің арасындағы
доғасы.
(Жауабы: 1.)
2.23. xydl , мұнда L : қабырғалары x 1 , y 1 болатын
L
квадрат контуры.
2.24.
(Жауабы: 0 .)
y dl , мұнда L : x t sin t , y 1 cos t циклоида2
L
1
.)
15
мұнда LABCD : төбелері A 2, 0 , B 4, 0 ,
сының бірінші аркасы. (Жауабы: 17
2.25.
xydl ,
LABCD
C 4, 3 , D 2, 3 болатын төртбұрыш контуры.
2.26.
ydl , мұнда L :
y2 2x
параболасының x 2 2 y
L
параболамен қиылған доғасы.
(Жауабы: 45.)
(Жауабы:
5 5 1 .)
3
dl
2.27.
, мұнда LAB : түзудің A 4, 0 мен B 6, 1
L AB x y
нүктелерінің арасындағы кесіндісі.
2.28.
x y dl ,
2
2 2
(Жауабы:
5
5 ln . )
4
мұнда L : 2 шеңберінің бірінші
L
ширектегі бөлігі. (Жауабы: 16 .)
334
23.
2.29.L AB
dl
, мұнда LAB : түзудің A 1,1,1 мен
x2 y 2 z 2
B 2, 2, 2 нүктелерін қосатын кесіндісі.
(Жауабы: ln 2 .)
2.30. x y dl , мұнда L : x 2 y 2 2 x шеңбері.
L
(Жауабы: 2 .)
3
3.1.
2 y 2 z 2 dl , мұнда
L:
x2 y 2 z 2 a2 ,
x y
L
(Жауабы: 2 a 2 .)
шеңбері.
xyzdl ,
3.2.
мұнда
L:
x2 y 2 z 2 R2 ,
x2 y 2
L
шеңберінің бірінші октанттағы бөлігі. (Жауабы: R 4
R2
4
3
.)
32
y
3.3. arctg dl , мұнда L : 2 – Архимед спиралінің
x
L
радиусі R центрі полюсте болатын дөңгелектің ішінде жатқан
3
доғасы. (Жауабы: R 2 4 2 8 /12 .)
3.4. x2 y 2 z 2 dl , мұнда L : x a cos t , y a sin t, z bt ,
L
3a 4 b . )
2
0 t 2 қисығы. (Жауабы: 2 a 2 b 2
2 2
3
3.5. 2 z x 2 y 2 dl , мұнда L : x t cos t , y t sin t , z t
L
– конустық винттік сызығының бірінші орамы.
3
(Жауабы: 2 2 1 2 2 2 1 / 3 .)
335
24.
1.17. u M x 2 y e z , M 1 4, 5, 0 , M 2 2, 3, 4 .1.18. u M x y 3 xyz , M1 2, 2, 4 , M 2 1, 0, 3 .
1.19. u M 3x 2 yz 3 , M1 2, 3,1 , M 2 5, 2, 0 .
1.20. u M e xy z , M 1 5, 0, 2 , M 2 2, 4, 3 .
2
1.21. u M x yz , M 1 3,1, 4 , M 2 1, 1, 1 .
1.22. u M x 2 y 2 z 2
, M 1, 2, 1 , M 0, 1, 3 .
3
2
2
1.23. u M x y , M 1 1, 5, 0 , M 2 3, 7, 2 .
z
1.24. u M x 2 y y 2 z 3 z , M1 0, 2, 1 , M 2 12, 5, 0 .
1.25. u M
10
, M 1 1, 2, 2 , M 2 2, 0,1 .
( x y 2 z 2 1)
2
1.26. u M ln 1 x2 y 2 z 2 , M1 1,1,1 , M 2 5, 4, 8 .
1.27. u M
x y z
, M1 1,1,1 , M 2 2, 3, 4 .
y z x
1.28. u M x 3 xy 2 6 xyz , M 1 1, 3, 5 , M 2 4, 2, 2 .
1.29. u M
x y x
, M 1 2, 2, 2 , M 2 3, 4, 1 .
y z z
1.30. u M e x yz , M 1 1, 0, 3 , M 2 2, 4, 5 .
2. S беті бойынша бірінші текті беттік интегралды есептеңіз,
мұнда
S – координаттық жазықтықтармен қиыл-ған
(p)
жазықтығының бөлігі.
2.1. (2 x 3 y 2 z ) dS , p : x 3 y z 3.
s
(Жауабы:
2.2. (2 y 7 x 9 z )dS , p : 2 x y 2 z 2.
15 11
.)
2
(Жауабы: 12 .)
s
355
25.
2.3. (6 x y 4 z )dS , p : 3x 3 y z 3.s
2.4. ( x 2 y 3 z ) dS , p : x y z 2.
(Жауабы:
19 19
.)
6
(Жауабы: 8 3 .)
s
2.5. (3x 2 y 6 z )dS , p : 2 x y 2 z 2.
(Жауабы:
s
2.6. (2 x 5 y z )dS ,
p : x 2 y z 2.
(Жауабы:
s
2.7. (5 x 8 y z )dS , p : 2 x 3 y z 6.
5
.)
2
7 6
.)
3
(Жауабы: 25 14 .)
s
2.8. (3 y x z )dS , p : x y z 2.
s
2.9. 3 y 2 x 2 z dS , p : 2 x y 2 z 2.
(Жауабы: 20 3 .)
3
(Жауабы: 3 .)
S
2.10. (2 x 3 y z )dS , p : x 2 y z 2.
(Жауабы:
6 .)
s
2.11. (5 x y z )dS ,
p : x 2 y 2z 2.
(Жауабы: 5 .)
s
2.12. (3x 2 y 2 z )dS , p : 3x 2 y 2 z 6.
(Жауабы: 9 17. )
s
2.13. (2 x 3 y z )dS , p : 2x y z 2.
(Жауабы: 2 6 .)
s
2.14. (9 x 2 y z )dS , p : 2 x y z 4.
(Жауабы: 40 6 .)
s
2.15. 3x 8 y 8 z dS , p : x 4 y 2 z 8.
(Жауабы: 96 21 .)
S
2.16. 4 y x 4 z dS , p : x 2 y 2 z 2.
(Жауабы: 1 .)
S
2.17. 7 x y 2 z dS , p : 3x 2 y 2 z 6.
S
(Жауабы: 17
17
.)
2
356
26.
2.18. 2 x 3 y z dS , p : 2 x 3 y z 6.(Жауабы: 18 14 .)
S
2.19. 4 x y z dS , p : x y z 2.
(Жауабы: 8 3 .)
S
2.20. (6 x y 8 z ) dS , p : x y 2 z 2.
(Жауабы: 6 6 .)
s
2.21. (4 x 4 y z ) dS , p : x 2 y 2 z 4.
(Жауабы: 44 .)
s
2.22. (2 x 5 y z ) dS , p : x y 2 z 2.
(Жауабы: 5 6 .)
s
2.23. (4 x y 4 z )dS , p : 2 x 2 y z 4.
(Жауабы: 44 .)
s
2.24. (5 x 2 y 2 z )dS , p : x 2 y z 2.
(Жауабы: 16
s
2.25. (2 x 5 y 10 z )dS , p : 2 x y 3z 6.
3
.)
6
(Жауабы: 56 14 .)
s
2.26. (2 x 15 y z )dS , p : x 2 y 2 z 2.
(Жауабы: 10 .)
s
2.27. (3 x 10 y z )dS , p : x 3 y 2 z 6.
(Жауабы: 35 14 .)
s
2.28. (2 x 3 y z ) dS , p : 2 x 2 y z 2.
(Жауабы:
s
2.29. (5 x y 5 z ) dS , p : 3x 2 y z 6.
7
.)
6
(Жауабы: 37 14 .)
s
2.30. ( x 3 y 2 z ) dS ,
p : 2x y 2z 2.
(Жауабы:
s
9
.)
2
3. Екінші текті беттік интегралды есептеңіз.
3.1. ( y 2 z 2 ) dydz , мұнда S : x 9 y 2 z 2 параболоид
s
357
27.
бетінің x 0 жазықтығымен қиылған бөлігі ( n нормаль векторы iортымен сүйір бұрыш жасайды).
(Жауaбы: 81 . )
2
2
2
2
2
3.2. z dxdy , мұнда S : x y 2 z 2 эллипсоид бетінің
S
сыртқы жағы.
(Жауабы: 0.)
3.3. zdxdy ydxdz xdydz , мұнда S : x 0 , y 0 , z 0 ,
S
x 1 , y 1 , z 1 жазықтықтарымен шенелген куб бетінің сыртқы
жағы.
(Жауабы: 3.)
3.4. z 1 dxdy , мұнда S : x 2 y 2 z 2 16 сфералық
S
(Жауабы 256 . )
2
3.5. yzdydz xzdxdz xydxdy , мұнда S : x y z 4 жазық-
беттің сыртқы жағы.
S
тығының координаттық жазықтықтармен қиылған жоғарғы жағы.
(Жауабы: 32.)
3.6. x 2 dydz y 2 dxdz z 2 dxdy , мұнда S : x 2 y 2 z 2 16
S
сферасының бірінші октантта жатқан бөлігінің жоғарғы жағы.
(Жауабы: 96 . )
3.7. xdydz ydxdz zdxdy , мұнда S : x 2 y 2 z 2 1 сфераS
сының сыртқы жағы.
(Жауабы: 4 . )
3.8. xzdxdy xydydz yzdxdz , мұнда S : x y z 1 жазықS
тығының
координаттық
жоғарғы жағы.
жазықтықтармен
1
(Жауабы: .)
8
қиылған
бөлігінің
358


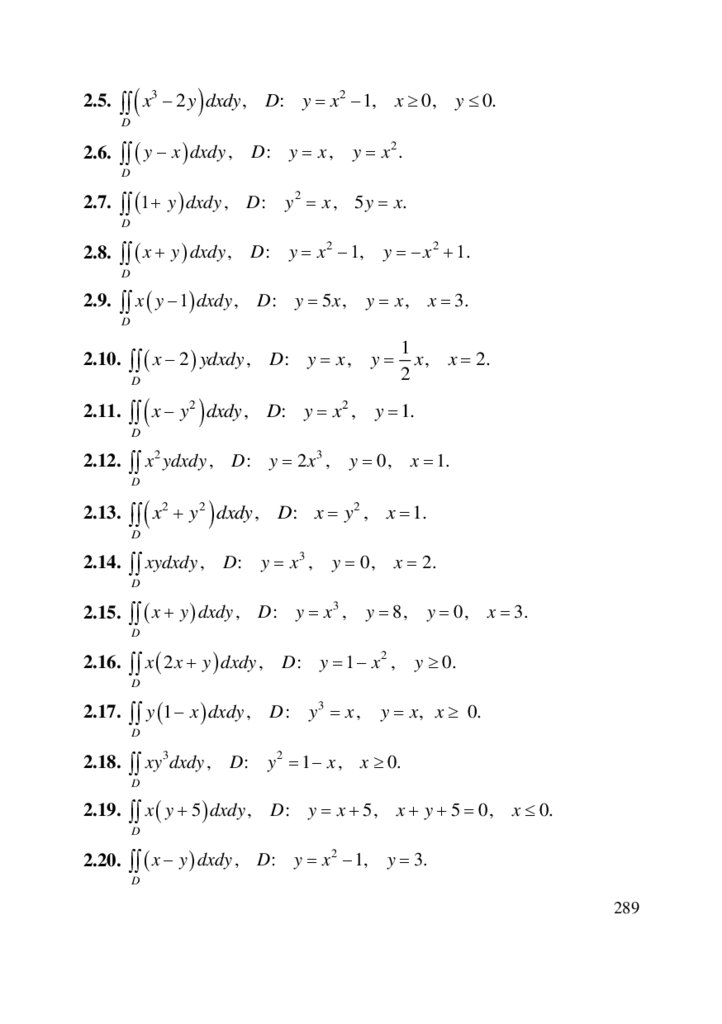
























 mathematics
mathematics








