Similar presentations:
Бірнеше айнымалысы бар көпмүшенің түрі және сипаттамасы
1.
КөпмүшелерБірнеше айнымалысы бар көпмүшенің түрі
және сипаттамасы.
2.
Өрнектерді қарап шығыңыз. Бір айнымалы көпмүшелердің қасына «˅» белгісін,бірнеше айнымалы көпмүше қасына «+» белгісін, көпмүше болып табылмайтын
өрнектер қасына «–» белгісін қойыңыздар.
a)2 x 5 x 4 3x 3 2 x 2 5
b)2 x3 x 3
с) x 4 xy 5 y
3
2
2
2
f ) x 2
x
h)t t 3t
3
3
d )16 y 7 72 y 6 108 y 5 54 y 4
e)3ab
g )2 x 2 5xy 2 y 2
k ) x 4x
3
5
3
l ) x 3 3x 2 5 х 15
3.
a)2 x x 3x 2 x 5 ˅5
4
3
b)2 x x 3
3
˅
с) x 4 xy 5 y
3
2
2
2
f ) x 2
x
2
˅
h)t t 3t ˅
3
3
+
d )16 y 7 72 y 6 108 y 5 54 y 4 ˅
e)3ab +
g )2 x 5xy 2 y
2
k)x 4x
3
5
3
˅
l ) x 3 3x 2 5 х 15
_
2
_
4.
Көпмүшенің анықтамасы!!! Дәреже көрсеткіштері теріс емес бүтін сан болу керек.
5.
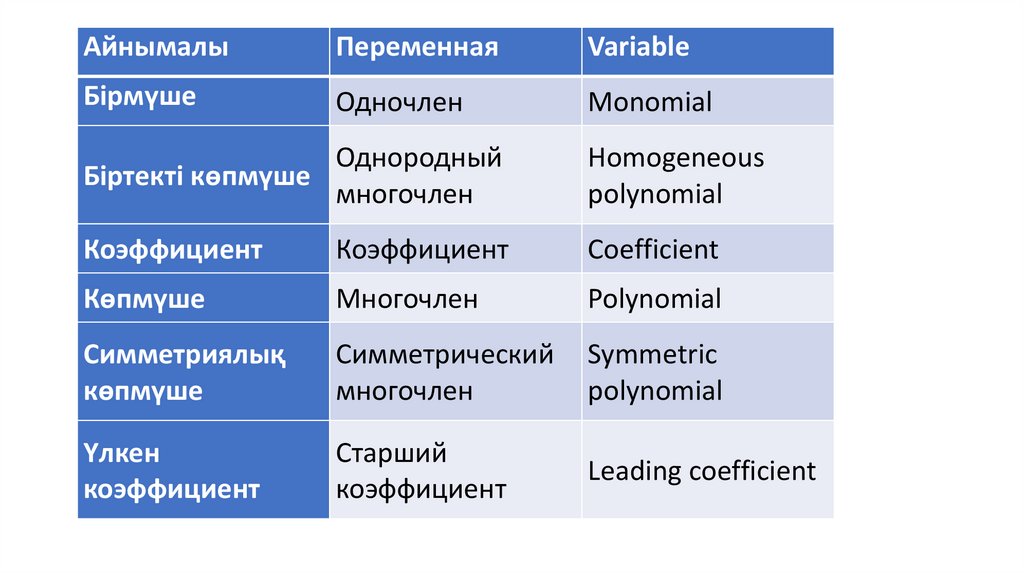
АйнымалыПеременная
Variable
Бірмүше
Одночлен
Monomial
Однородный
Біртекті көпмүше
многочлен
Homogeneous
polynomial
Коэффициент
Коэффициент
Coefficient
Көпмүше
Многочлен
Polynomial
Симметриялық
көпмүше
Симметрический
многочлен
Symmetric
polynomial
Үлкен
коэффициент
Старший
коэффициент
Leading coefficient
6.
Көпмүшелерді қосу және азайту7.
8.
9.
Тапсырма №2Көпмүшенің дәрежесі мен коэффициенттерін жазыңыз.
коэфициенттен бастаңыз.
Көпмүшенің коэффициенттерінің қосындысын табыңыз.
P( x) x 4 x 6 x 10 x 20
Q(x) = 2x3 -x+4
4
3
F(x) = 2x4+5x2-1
2
Бас
10.
Қосымша №2Тапсырма№1.
көпмүшені канондық түрде жазыңыз
а) (х + 1)(х - 1)(х - 2);
б)
(х + 1)2(х - 2) - (х + 1)(х - 2)2,
в)
(2х + 1)(2х - I)2;
г)
(2х + 1)(2х - I)2 + (1 - 2х)3
11.
Тапсырма №2f ( x ), g ( x )
көпмүшелері берілген. Кестеге дәреже көрсеткішін
толтырыңыздар
7
3
3
7
5
7
4
3
7
8
14
15
9
6
21
12.
f ( x, y, z ) x y 2 z2
2
2
q( x, y, z ) 2 x xy z
2
2
2
g ( x, y, z ) x y z 4 xyz
3
3
3
13.
Бірнеше айнымалы көпмүшеn-ші дәрежелі біртектi көпмүше
деп аталады, егер көпмүшенің әрбір
мүшесінің дәреже көрсеткіштерінің
қосындысы n-ге тең болса.
14.
Екі айнымалы p ( x, y ) көпмүшесініңx және у айнымалыларын сәйкесінше
у және x айнымалыларына
ауыстырғаннан көпмүше өзгермейтін
болса, онда p ( x, y ) көпмүшесі
симметриялы көпмүше деп аталады,
15.
Көпмүшені стандарт түрде жазыңыза) (2х-у-3)2+(х-Зу-1)2;
б)
(х - у - 2z - 1)2 + (2х+ у + z - З)2;
в)
(5х - у - 2)2 + 2(3х - у -1)2;
г)
(х - Зу + z - 2)2 - 3(2х + у - z + 1).


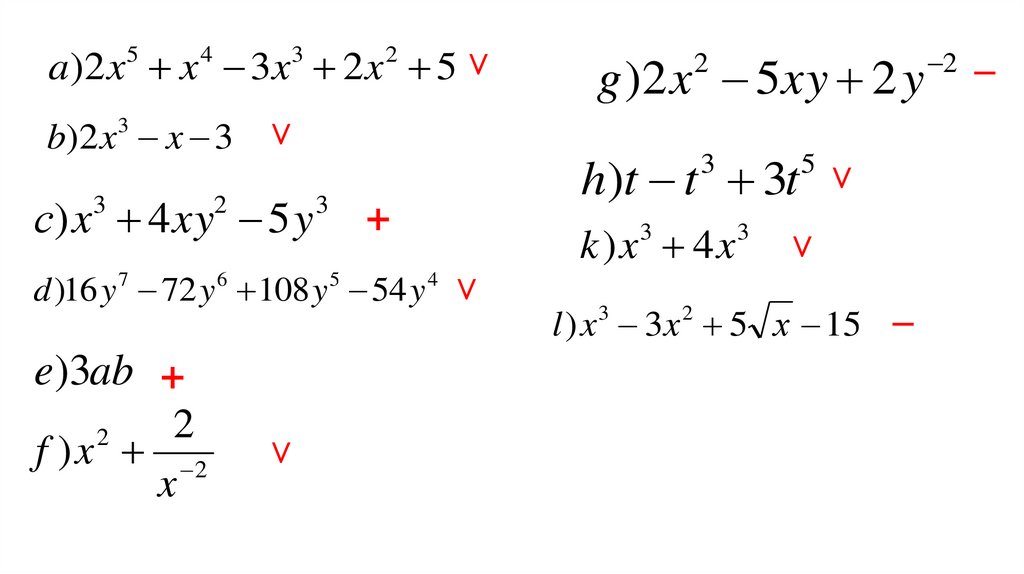







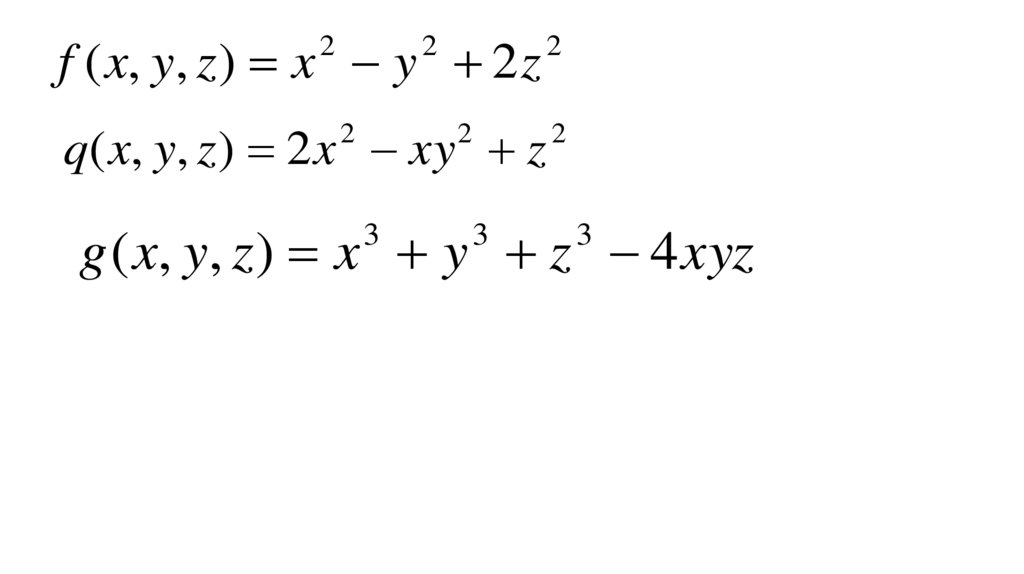



 mathematics
mathematics








