Жазық фигура ауданы

1. Анықталған интегралдың көмегімен жазық фигуралардың ауданы мен айналу денелерінің көлемін есептеу

2. Оқу мақсаты:

11.3.1.6 - берілген сызықтармен
шектелген жазық фигураның ауданын
есептеу;

3.

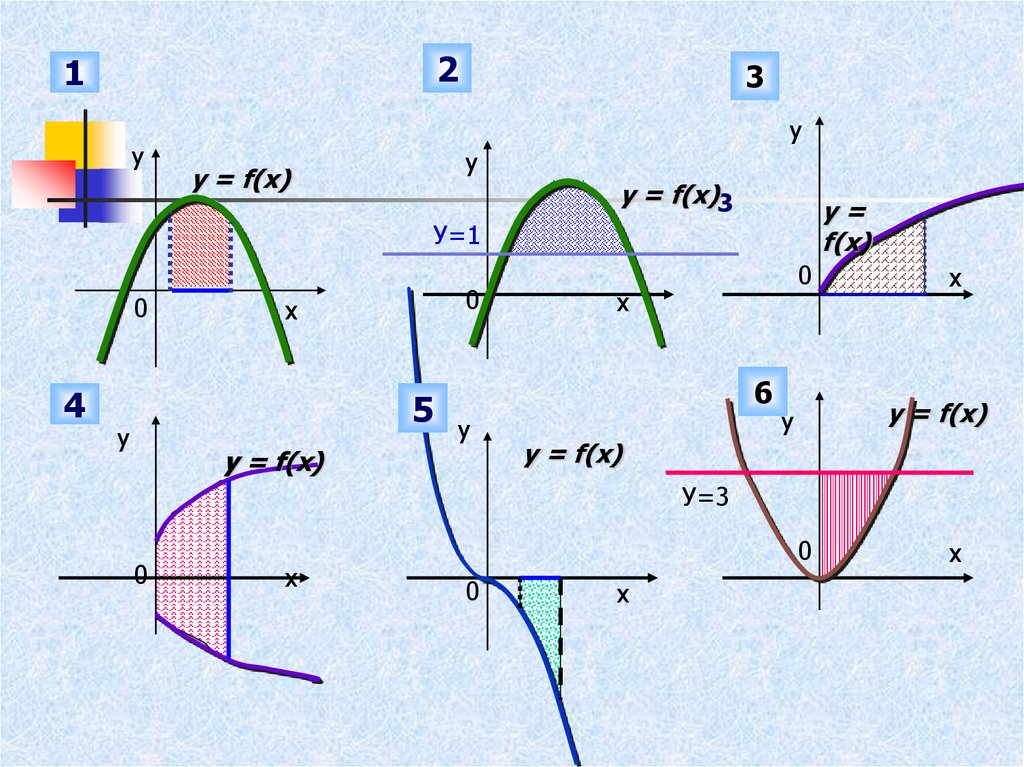
Суреттегі штрихталған фигуралардың
қайсысы қисық трапеция болып табылады
және қайсысы жоқ?
Таблицаны толтырыңыз
№1
№2
№3
№4
№5
№6
ия/жоқ

4.

2
1
у
3
у
у
y = f(x)
y = f(x)3
y=
f(x)
У=1
0
4
0
х
5
у
0
х
6
у
y = f(x)
y = f(x)
х
y = f(x)
у
У=3
0
х
0
0
х
х

5.

Ньютона-Лейбница формуласы
S F (b) F (a )
b
f ( x)dx F (b) F (a)
a
b
1643—1727
f ( x)dx F (b) F (a)
a
b
S f ( x)dx
a
1646—1716

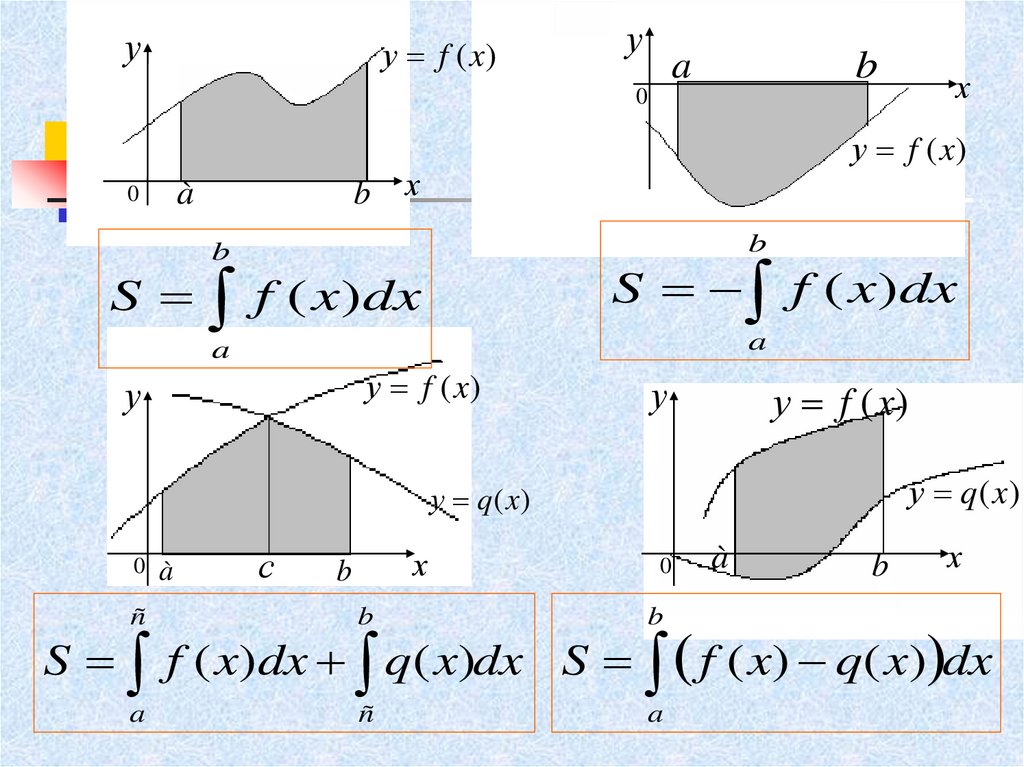
6.

у
у f (x)
у
a
b
0
à
0
b
у f (x)
х
b
b
S
S f ( x)dx
f ( x) dx
a
a
у f (x)
у
у f (x)
у
у q (x )
у q (x )
0
à
х
с
х
b
0
ñ
b
b
a
ñ
a
à
b
х
S f ( x)dx q( x)dx S f ( x) q( x) dx

7.

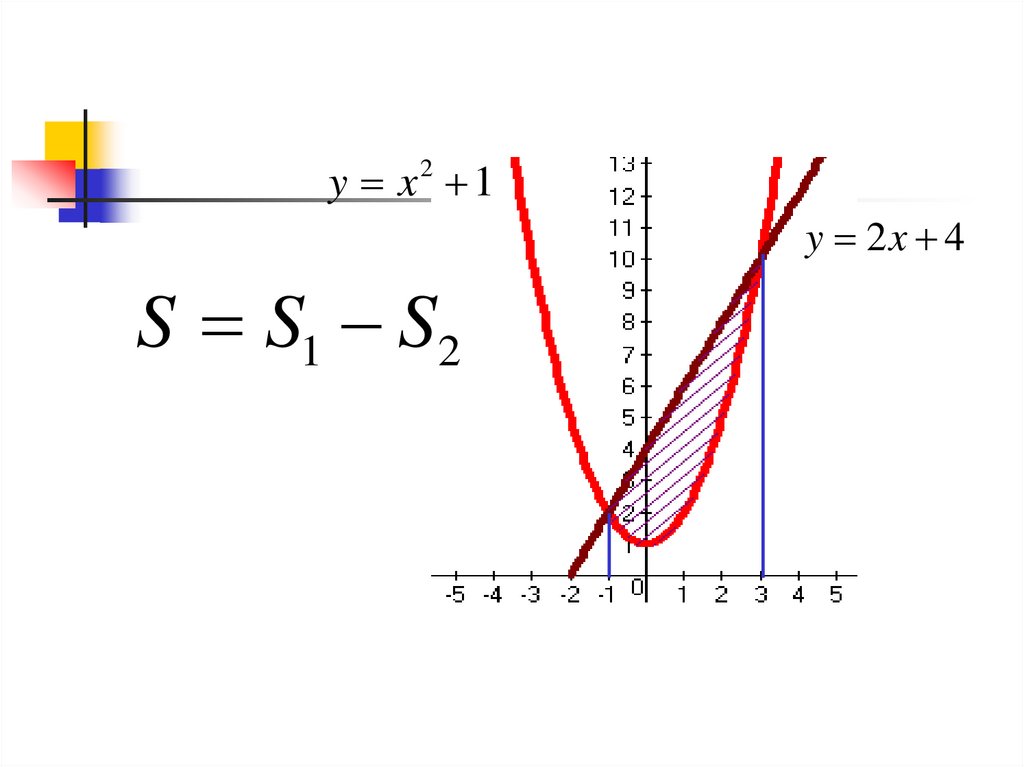
y x2 1
y 2x 4
S S1 S2

8.

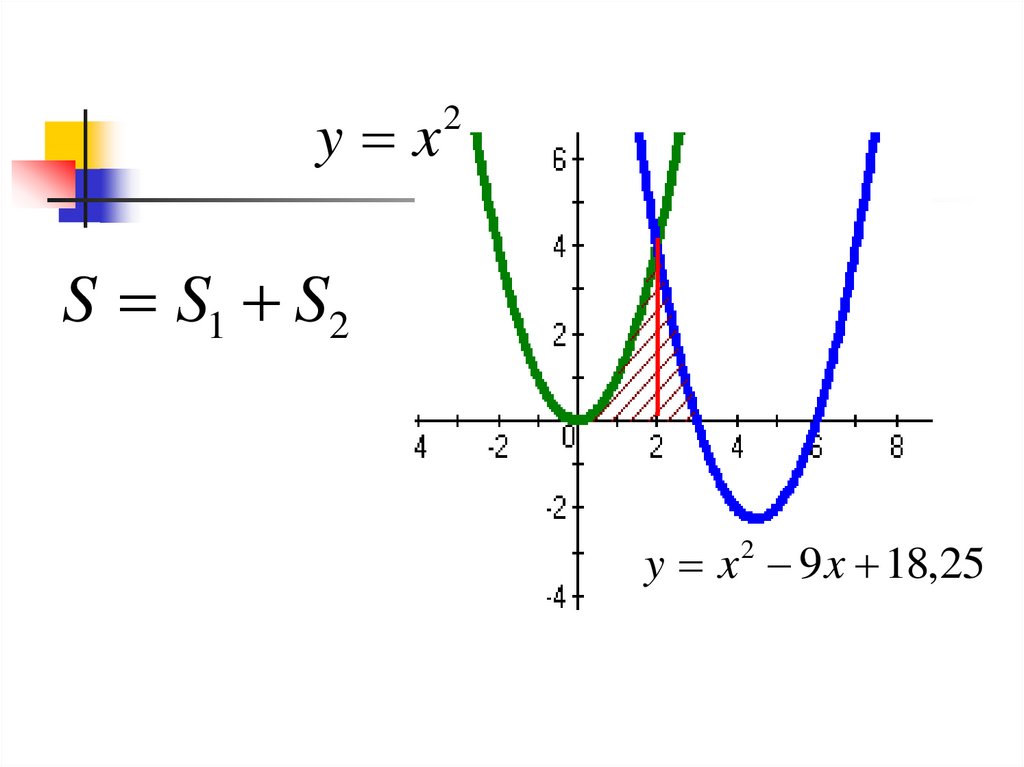
y x
2
S S1 S2
y x 2 9 x 18,25

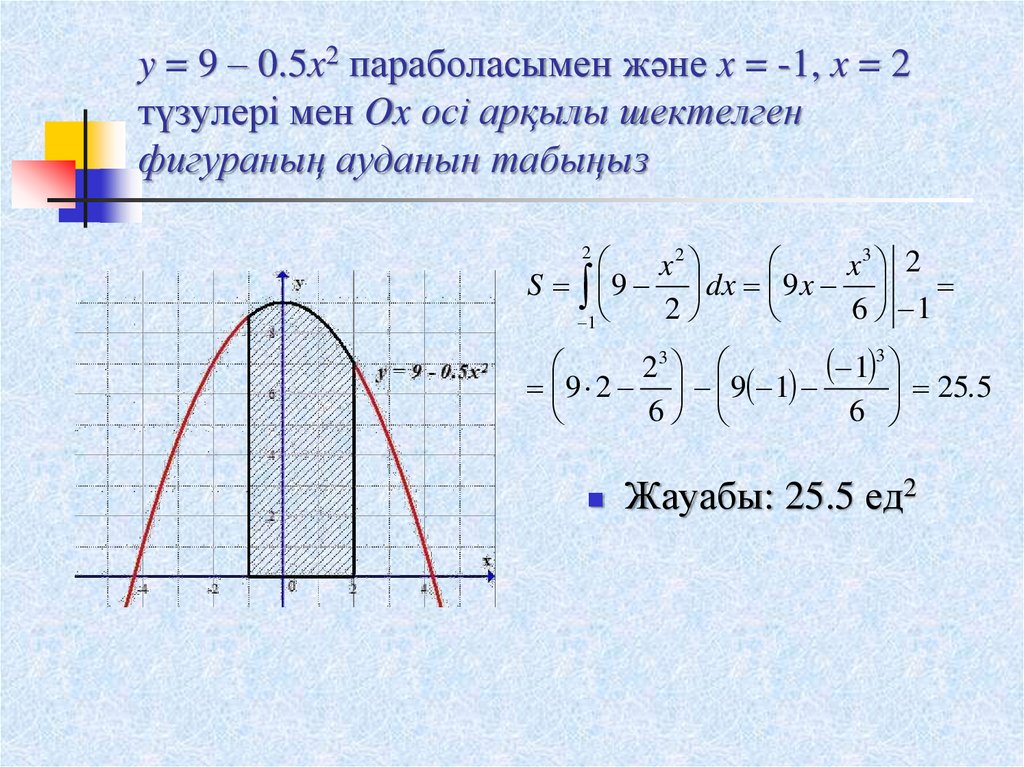
9. y = 9 – 0.5x2 параболасымен және x = -1, x = 2 түзулері мен Ox осі арқылы шектелген фигураның ауданын табыңыз

x2
x3 2
S 9 dx 9 x
2
6 1
1
2
3
23
1
9 2 9 1
25.5
6
6
Жауабы: 25.5 ед2

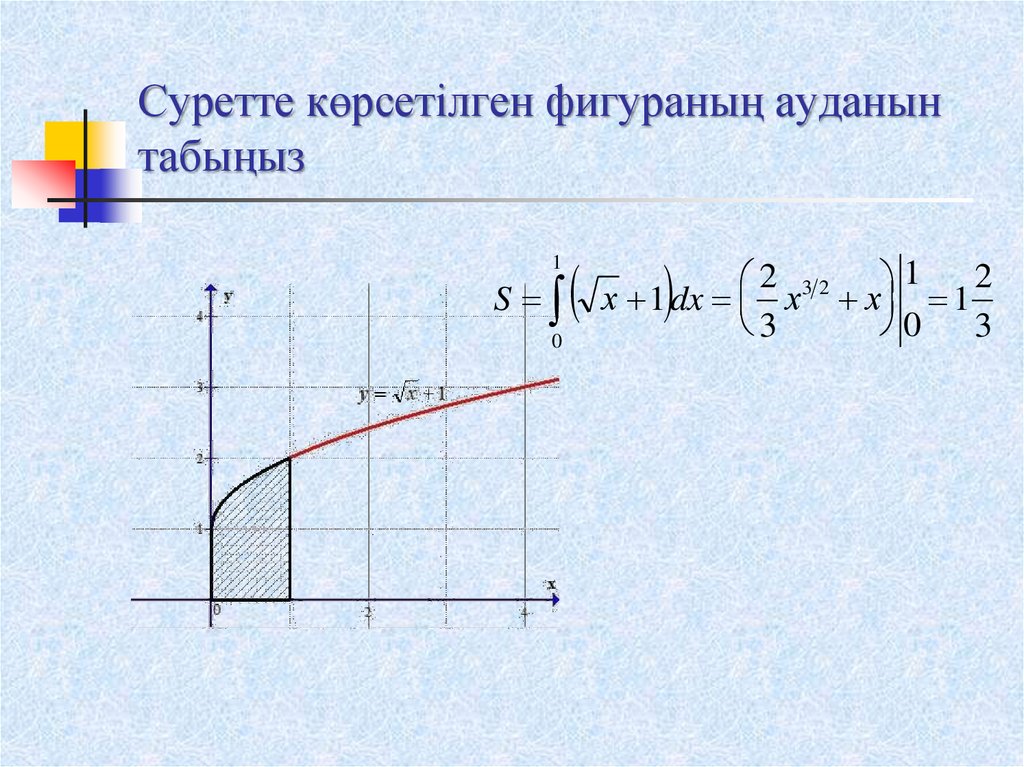
10. Суретте көрсетілген фигураның ауданын табыңыз

1
S
0
2
2 32 1
х 1 dx х х 1
3
0
3

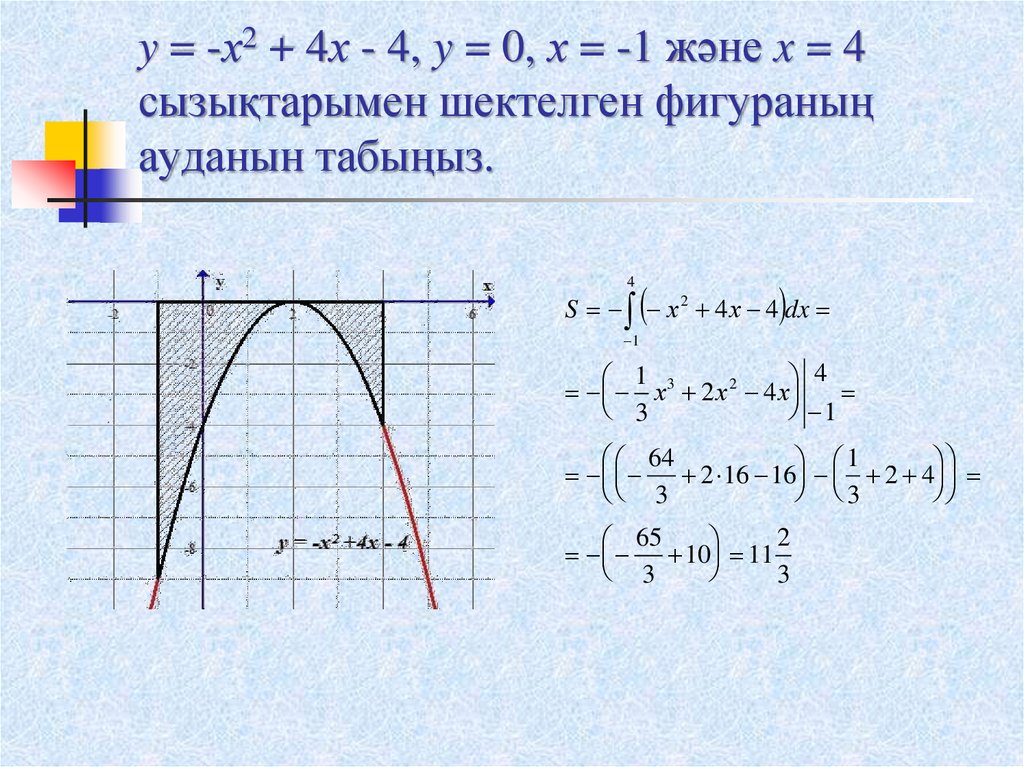
11. y = -х2 + 4х - 4, y = 0, х = -1 және x = 4 сызықтарымен шектелген фигураның ауданын табыңыз.

4
S х 2 4 х 4 dx
1
1
4
х 3 2 х 2 4 х
3
1
64
1
2 16 16 2 4
3
3
2
65
10 11
3
3

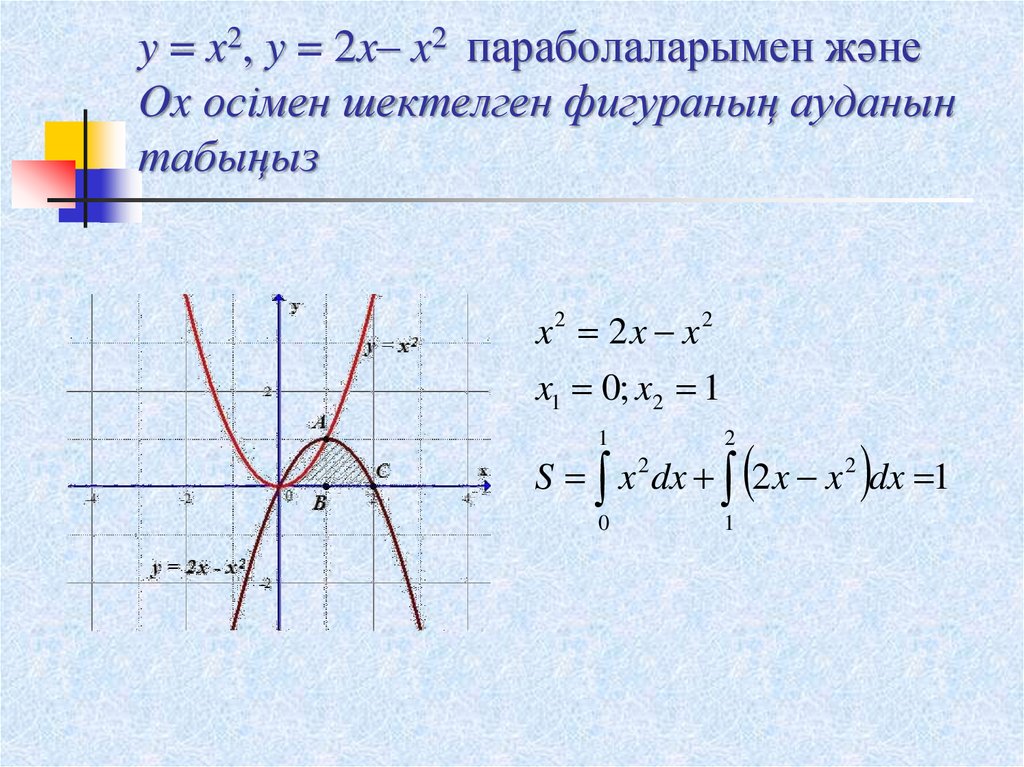
12. y = x2, y = 2x– x2 параболаларымен және Ox осімен шектелген фигураның ауданын табыңыз

x2 2x x2
x1 0; x2 1
1
2
0
1
S x 2 dx 2 x x 2 dx 1

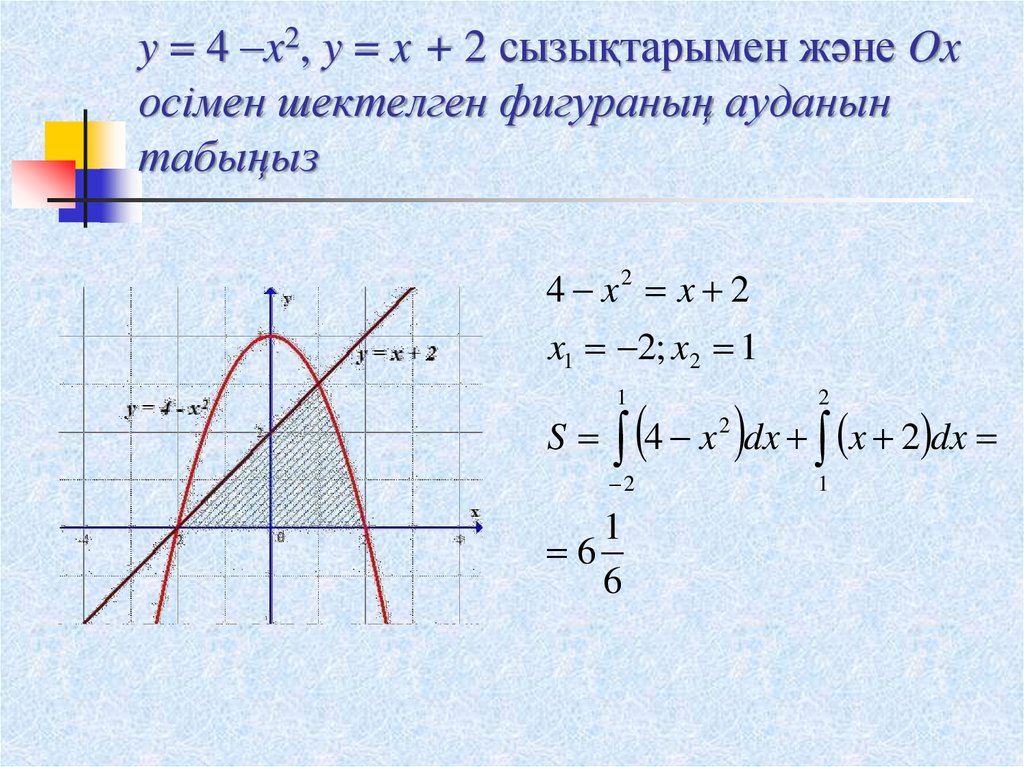
13. y = 4 –x2, y = x + 2 сызықтарымен және Ox осімен шектелген фигураның ауданын табыңыз

4 x2 x 2
x1 2; x2 1
4 x dx x 2 dx
1
S
2
2
2
1
6
6
1

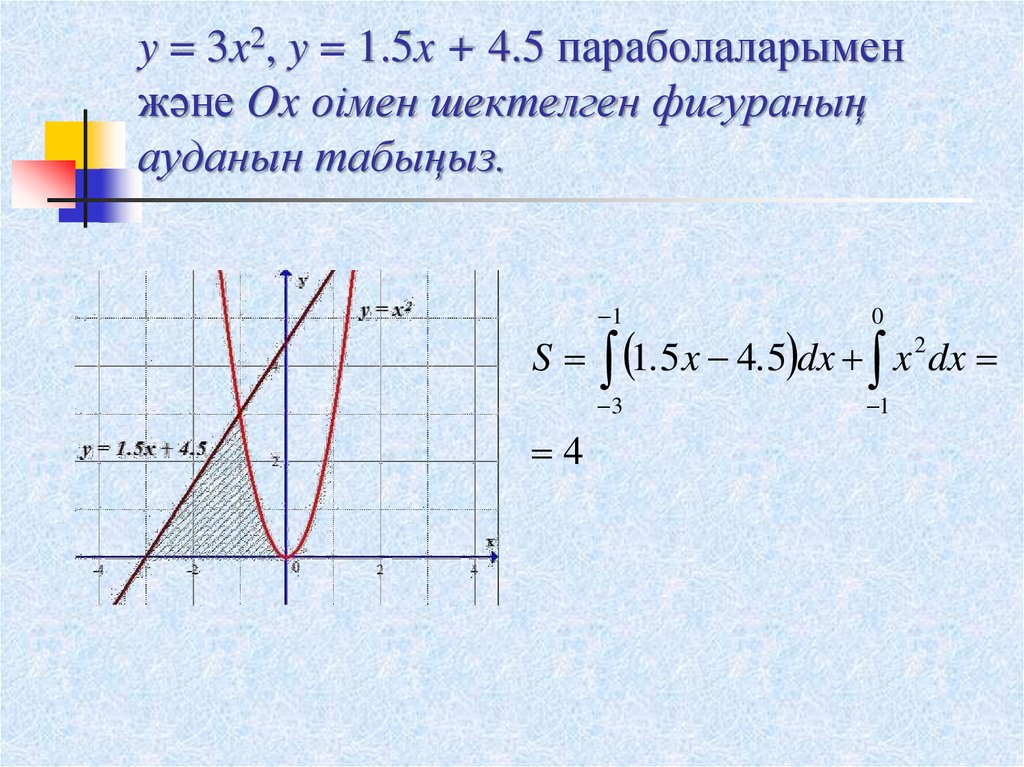
14. y = 3x2, y = 1.5x + 4.5 параболаларымен және Ox оімен шектелген фигураның ауданын табыңыз.

S
4
1
0
3
1
2
1
.
5
x
4
.
5
dx
x
dx