Similar presentations:
Жазықтықтың жалпы теңдеуі
1. Жазықтықтың жалпы теңдеуі.
2. Жазықтықтың теңдеуі
xcosα+ycosβ+zcosγ–p = 0түріндегі теңдеуді жазықтықтың нормаль теңдеуі деп
атаймыз.
мұндағы cosα, cosβ, cosγ – бағыттаушы косинутар.
Декарттық координаталар жүйесінде кез келген
жазықтықтың теңдеуі мына түрде беріледі
Ax + By + Cz + D = 0, (1)
мұндағы A, B, C, D – берілген сандар, сонымен қатар
A2 + B2 + C2 ≠ 0.
(1) теңдеу жазықтықтың жалпы теңдеуі деп аталады.
А,В,С коэффициенттері (1) теңдеумен берілген
жазықтыққа перпендикуляр n векторының
координаталары.
n векторы жазықтықтың нормаль векторы деп аталады.
3. Жазықтық теңдеуі
A (x – xo) + B (y – yo) + C (z – zo) = 0,теңдеуі берілген М (xo,yo,zo) нүктесі және
n A, B, C нормаль векторы арқылы берілген
жазықтықтың теңдеуі.
x y z
1
(2)
a b c
a
D
D
D
, b , c
A
B
C
мұндағы
– алгебралық
шамалар. (2) теңдеу жазықтықтың кесіндідегі
теңдеуі деп аталады.
4. Жазықтықтың орналасуы
1. D = 0, онда Ax + By + Cz = 0 жазықтығы координатабасынан өтеді.
2. C = 0, онда Ax + By + D = 0 жазықтығы Oz осіне
параллель. Дәл осылай Ax + Cz + D = 0 жазықтығы Oy
осіне және By + Cz + D = 0 жазықтығы Ox осіне параллель
болады.
3. С = 0 және D = 0, Ax + By = 0, Ax + Cz = 0, By + Cz = 0,
сәйкес Oz, Oy, Ox осінен өтетін жазықтық теңдеуі.
4. В = С = 0, онда Ax + D = 0 жазықтығы yOz
координаталық жазықтығына параллель. Сонымен қатар
By + D = 0 және Cz + D = 0 жазақтықтары сәйкесінше
xOz және хOy координаталық жазықтықтарына параллель.
5. B = C = D = 0, Ax = 0 немесе x = 0. yOz координаталық
жазықтықтың теңдеуі. Дәл осылай Bсy = 0, Cz = 0 немесе y
= 0, z = 0, сәйкесінше xOz және хOy координаталық
жазықтықтарының теңдеуін береді.
5. Екі жазықтықтың арасындағы бұрыш.
Қиылысатын екі жазықтықтың арасындағы бұрыш депосы жазықтықтар анықтайтын сыбайлас екі жақты
бұрыштардың шама жағынан кішісін айтады.
n1 ( A1 , B1 , C1 ) және n2 ( A2 , B2 , C2 ) берілген жазықтықтың
нормаль векторлары.
Екі жазықтықтың арасындағы бұрыш :
α1 : A1x + B1y + C1z + D1 = 0,
α2 : A2x + B2y + C2z = D2 = 0,
төмендегі формуламен анықталады
n n
cos cos n1 n2 1 2
n1 n2
A1 A2 B1B2 C1C 2
A12 B12 C12
A22 B22 C 22
6. Жазықтықтың параллельдік және перпендикулярлық шарттары
Жазықтықтың параллельдік шартыn1 n2 немесе
A1 B1 C1 D1
A2 B2 C 2 D2
Жазықтықтың перпендикулярлық шарты
n1 n2 0 немесе A1A2 + B1B2 + C1C2 = 0.
7. Нүктеден жазықтыққа дейінгі қашықтық.
M1 (x1, y1, z1) нүктесіненxcosα+ycosβ+zcosγ–p = 0 жазықтығына дейінгі
қашықтық
d=| x1cosα +y1cosβ+zcosγ –p|
формуласымен анықталады.
ал Ax + By + Cz + D = 0 жазықтығына дейін
d
Ax1 By1 Cz1 D
A B C
2
2
2
8. Кеңістікте түзу келесі әдістермен беріледі:
1.A1 x B1 y C1 z D1 0
A2 x B2 y C 2 z D2 0
(3)
өзара қиылысатын екі жазықтықтың теңдеулер
жиынын осы жазықтықтардың қиылысу
сызығын анықтайтын түзудің теңдеуі ретінде
қарастыруға болады.
(3) -кеңістіктегі түзудің жалпы теңдеуі.
9. 2. Түзудің параметрлік түрде берілген теңдеуі
x x1 mt,y y1 nt ,
z z pt ,
1
t – кез келген нақты сан, параметр,
a(m, n, p) түзудің бағыттаушы векторы.
10. Түзудің канондық теңдеуі:
x x1 y y1 z z1m
n
p
немесе М1 (x1, y1, z1) нүктесі арқылы өтетін және
m, n, p векторына параллель түзудің теңдеуі.
М1 (x1, y1, z1) және М2 (x2, y2, z2) нүктелері арқылы
өтетін түзудің теңдеуі:
x x1
y y1
z z1
x2 x1 y 2 y1 z 2 z1
11. Екі түзу арасындағы бұрыш
Кеңістіктегі екі түзу арасындағы бұрышдеп бір нүктеден сол түзулерге параллель
жүргізілген түзулердің қиылысуынан
пайда болған бұрыштардың кез келгенін
айтады.
l1:
x x1 y y1 z z1
m1
n1
p1
cos
x x1 y y1 z z1
l2:
m2
n2
p2
m1m2 n1n2 p1 p2
m12 n12 p12 m22 n22 p22
12.
l1 және l2 түзулерінің перпендикулярлықбелгісі
m1 · m2 + n1 · n2 + p1 · p2 = 0.
Осы түзулердің параллельдік белгісі:
m1 n1
p1
m2 n2 p 2
13. Түзу мен жазықтық арасындағы бұрыш
Түзу мен жазықтық арсындағы бұрыш деп, түзу меноның жазықтыққа проекциясының арасындағы сыбайлас
екі бұрыштың кез келгенін айтады.
Жазықтық жалпы теңдеуімен берілсін
Ax + By + Cz + D = 0, ал түзу канондық теңдеуімен
берілсін x x y y z z
1
m
1
n
1
p
Түзу мен жазықтық арсындағы бұрыш
sin
Am Bn Cp
A B C
2
2
2
m n p
2
2
2
14.
Түзу мен жазықтықтың параллельдік шарты:Am + Bn + Cp = 0.
Түзу мен жазықтықтың перпендикулярлық шарты
:
A B C
m n p
15.
Егер параллельдік шарты орындалмасаx x1 y y1 z z1
m
n
p
түзуі мен Ax + By + Cz + D = 0 жазықтығы
қиылысады.
Қиылысу нүктесін табу үшін келесі жүйені шешу
керек:
x x1 y y1 z z1
,
n
p
m
Ax By Cz D 0.
16. Қолданылған әдебиеттер:
1. И.В. Павлушков и др. Основы высшей математики иматематической статистики. (учебник для медицинских и
фармацевтических вузов)., М., 2003 г.
2. В.С. Шипачев. Курс высшей математики. М., Проспект.
2004 г.
3. И.И. Баврин, В.Л. Матросов. Высшая математика. М.,
ВЛАДОС.2002г.
4. Ю. Морозов. Основы высшей математики для мед. вузов.
М., 2000 г.
17.
Назараударғандарыңызға
рахмет













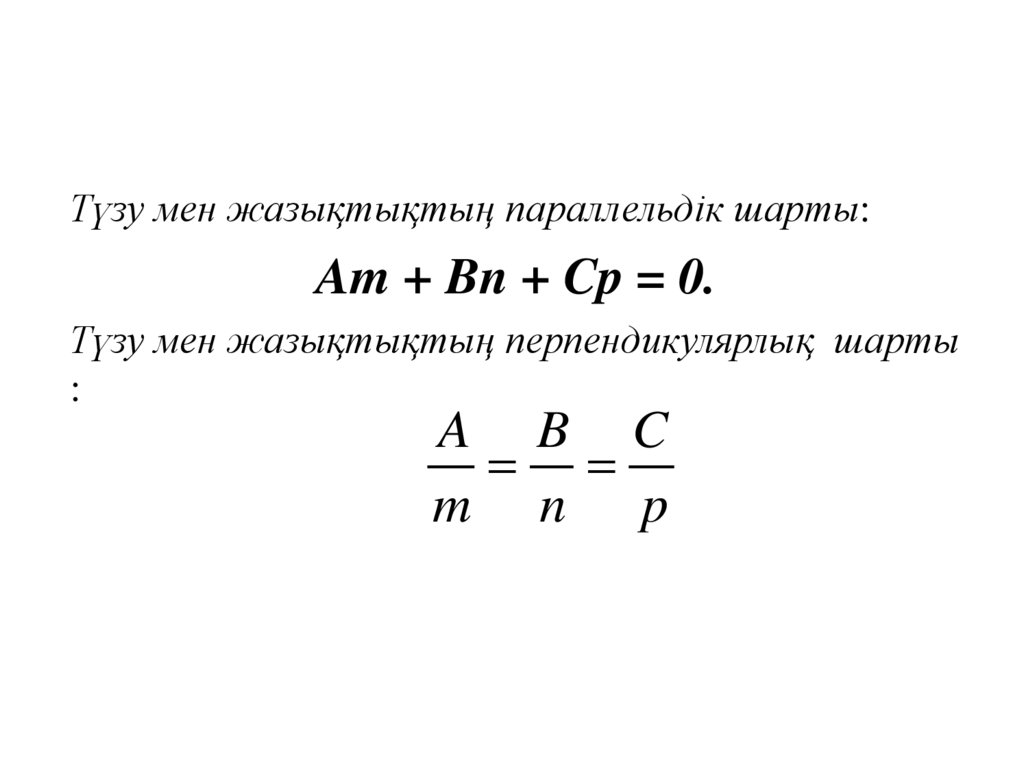



 mathematics
mathematics








